岸桥斜撑的抗震拓扑优化

王兴锋，张 氢，秦仙蓉，孙远韬

（同济大学机械与能源工程学院，上海201804）

岸桥是大型的机械装备，广泛应用于集装箱港口。岸桥正朝着大型化趋势发展，使其更容易遭受地震灾害的影响［1-2］。为确保岸桥在地震之后仍然能够正常运行，发挥物资装卸的功能，迫切需要对岸桥的抗震设计展开研究。

为防止岸桥在地震下发生破坏，Lifttech公司提出了多种抗震设计方法［2］，包括在下部门框（见图1）的门腿-下横梁连接处设置斜撑，用特殊抗弯框架的设计方法增加下部门框的延性，或者在下部门框与上部门框之间设置隔震装置等。王贡献等［3］提出在下部门框的门腿-下横梁连接处设置黏滞阻尼器，以耗散地震输入能量，减小门框结构的水平位移。除了下部门框，岸桥上部门框中的斜撑对整体结构的抗震性能也有较大影响。Lifttech公司提出用摩擦阻尼器代替传统的钢管支撑［4］，以提高对地震输入能量的耗散能力。滕媛媛等［5］通过数值仿真和实验研究，也证明摩擦阻尼器可有效提高岸桥的抗震性能。

由以上研究可知，上部门框和下部门框是岸桥抗震设计时重点关注的区域。对这些区域的强化都可以在一定程度上提高岸桥的抗震能力。但如何选择待强化的区域，才能用最经济的手段满足岸桥的抗震性能要求，这一问题尚未被关注，更没有合理的解决方案。针对这一问题，本文提出用斜撑对岸桥的上下框架进行强化，用拓扑优化的方法来决定斜撑的最优布置方案，并通过对岸桥实例的优化分析进行了验证。

图1 岸桥结构示意图Fig.1 Structure of container crane

1 岸桥的力学模型

由前人的研究［2-5］可知，通过强化岸桥的上、下门框可有效提高岸桥的抗震能力。因此，在岸桥的抗震设计中，可以将岸桥简化为仅包含上、下门框的框架结构（见图2）。同时，根据岸桥的质心位置，将岸桥的所有质量等效分配到上横梁、下横梁的两个端点。

在常规的岸桥设计中，斜撑和上横梁通常都采用普通钢管。但在地震载荷作用下，岸桥发生摆动，斜撑需要承担往复的拉压载荷。由于斜撑的长度很大，长细比也比较大，斜撑的实际抗压能力远小于抗拉能力，材料的利用率不充分。在钢框架结构的抗震设计中，屈曲约束支撑（Buckling Restrained Brace，BRB）在受拉与受压时均能达到屈服，具有比传统支撑更稳定的力学性能［6］，材料利用率更高，应用广泛。故本文采用BRB支撑代替传统的钢管支撑，进行岸桥的抗震设计。

图2 岸桥的简化模型Fig.2 Simplified model of container crane

2 岸桥斜撑的抗震拓扑优化

2.1 抗震性能水平和性能指标

确定合理的抗震性能水平及性能量化指标，是岸桥抗震设计的关键。杨毅等［7］定义了岸桥的3种破坏等级，在此基础之上提出了3个性能水平（包括正常运行、修复运行和防止倒塌），并用下部门框的水平位移角作为性能的量化指标。采用水平位移角可描述岸桥的水平变形情况，但是岸桥的上、下框架多采用箱型截面，箱型截面中的加筋情况复杂，难以准确定义水平位移和构件弹塑性变形之间的关系。构件的弹塑性变形能够直接反映结构的损伤情况，是一种重要的结构性能指标。在岸桥结构中，构件的弹塑性变形可间接反映结构的整体水平变形，所以使用构件的弹塑性变形作为岸桥的抗震性能指标，是一种更合理的方法。

鉴于岸桥在物资装卸过程中的重要作用，必须要求岸桥在大震后仍然保持大部分甚至全部的装卸能力。基于这个要求，定义一种新的岸桥抗震性能水平：在地震作用下，岸桥的主体结构（如横梁、立柱、门腿等）不发生塑性变形，而其他构件（如斜撑）可发生一定程度的塑性变形。通过斜撑的弹塑性变形，可消耗很大一部分的地震输入能量，从而保护主体结构不发生损伤。BRB支撑具有饱满的滞回曲线［6］，耗能能力更强，更适合充当结构中的塑性耗能元件。基于BRB支撑的钢框架抗震设计，已经得到了比较广泛的应用［8-9］。

2.2 抗震拓扑优化的数学模型

岸桥在地震作用下，首先必须满足力的平衡约束：

式中：Q为梁或柱的内力，包含轴力和两端的弯矩；Qc为斜撑的内力；F为节点的外力，包括自重和地震载荷；C、Cc分别为梁柱内力、斜撑内力和节点外力的相容性矩阵。

梁或柱的内力和节点位移之间应满足如下约束：

式中：K为梁或柱的正交单元刚度矩阵，可参考文献［10］附录A进行计算；U为节点位移。

采用理想弹塑性模型描述斜撑的变形情况，故斜撑的内力和节点位移之间应满足如下约束：

式中：Kc为斜撑的刚度；Nc为斜撑屈服函数的单位外法向量矩阵；Zc为斜撑的塑性变形量，且Zc≥0。

由于采用了理想弹塑性模型，故斜撑的内力应不超过斜撑的极限承载能力：

式中：wc为斜撑的屈服函数；rc为斜撑的极限承载能力。

为保证斜撑不发生塑性破坏，斜撑只能发生一定程度的塑性变形：

式中：[Zc]为斜撑塑性变形的上限值。

为确定斜撑在任意一个时刻是处于弹性状态还是塑性状态，需增加一组正交约束［11］：

为保证梁或柱在地震时始终保持弹性状态，参考LRFD-AISC［12］对梁或柱的内力施加如下约束：

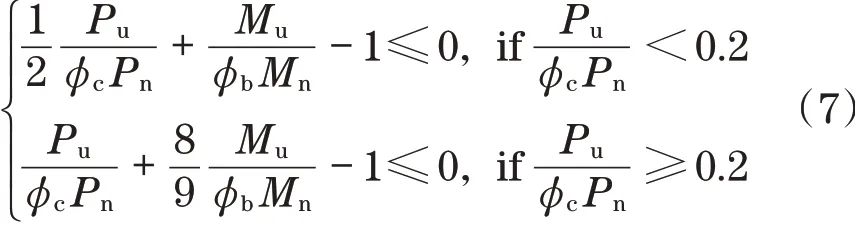
式中：Pu为梁或柱的轴力；Pn为梁或柱的轴向承载能力；φc为轴向抗力折减系数；Mu为梁或柱的弯矩；Mn为梁或柱的抗弯承载能力；φb为弯曲抗力折减系数。

岸桥斜撑的大小由BRB支撑的芯材面积决定，从工程实际角度出发，芯材截面面积需满足一定的上下限约束：

式中：Ai为第i个斜撑中的芯材面积；AL为芯材面积的下限值；AU为芯材面积的上限值。为实现斜撑的拓扑优化，将AL设置为一个接近于零的值，当斜撑芯材的面积小于等于AL时，即认为斜撑可以被删除。

岸桥抗震设计的成本与BRB支撑的材料用量直接相关，故可以将拓扑优化的目标函数定义最小化BRB支撑的芯材用量。岸桥斜撑的塑性抗震拓扑优化数学模型可定义为

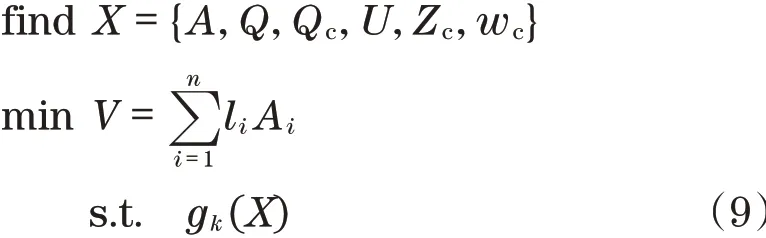
式中：li为第i个斜撑的长度；gk(X)为对应于第k个约束方程组，1≤k≤8。

若期望岸桥在地震作用下完全不发生结构损伤，可将BRB支撑的变形限制在弹性范围内。相应地，需要将式（3）、式（5）、式（6）简化为如下约束条件：

岸桥斜撑的弹性抗震拓扑优化数学模型可定义为

式中：gk(X)为对应于第k个约束方程组，k=1，2，4，7，8，10。

3 数值实验

采用基结构法建立岸桥抗震拓扑优化的初始结构。在建立岸桥的初始结构时，应尽可能地包含潜在支撑，同时又要避免改变原有杆件的受力特征。例如，在原有的岸桥结构中，上横梁为二力杆件，故应避免在上横梁的中点处设置支撑的节点。

图3 （a）中，G1、G2为自重载荷，F1、F2为地震载荷。根据岸桥的实际重量和质心位置，G1、G2分别取287.5 t和87.5 t。地震载荷F1、F2的计算方法为

式中：keq为地震载荷系数，可参考文献［13］中的表1进行选取。为使岸桥能够抵抗罕遇地震，取地震烈度12级，对应的keq为0.8。

图3 岸桥拓扑优化算例Fig.3 Numerical example for topology optimization of container crane

表1 给出了部分杆件的尺寸。其中，h为腹板高度，bf为腹板内壁间距，tf为翼缘板厚度，tw为腹板厚度。其余杆件为BRB支撑，考虑到岸桥的实际情况，对杆件8进行尺寸设计，对应的截面尺寸约束为10-2m2≤A8≤10-1m2。对杆件4～7进行拓扑—尺寸优化，对应的截面尺寸约束为10-4m2≤Ai≤10-1m2(i=1，2，…，15)。当BRB支撑的芯材截面面积等于下限值时，就认为支撑可以被删除。取弹性模量为2.1×105MPa，箱型梁柱的屈服强度为345 MPa，BRB支撑芯材的屈服强度为235 MPa。

表1 箱型截面的尺寸Tab.1 Dimensions of box sections mm

岸桥斜撑的抗震拓扑优化数学模型中，包含了多组非线性约束。本文采用非线性优化求解器CONOPT［14］求解岸桥的抗震拓扑优化问题。CONOPT只能求解得局部最优解，但已经能够满足工程实际的需要。在GAMS［15］中对岸桥斜撑的塑性抗震拓扑优化问题、弹性抗震拓扑优化问题分别进行建模和求解，优化结果如表2所示。

从表2可知，无论是弹性拓扑优化还是塑性拓扑优化，对应的岸桥斜撑布置方案中第6、7组杆件均被删除，其余杆件保留，斜撑的布置方案非常明确。考虑塑性变形的拓扑优化可以更充分地利用材料的变形能力，需要的材料更少，抗震设计成本更低。需要说明的是，由于横梁3的截面宽度较大，所以在布置第5组斜撑时可前后错开，从而避免使斜撑交叉。

岸桥上下框架的水平位移角如图4所示。即使当[Zc]=6.0[ε]时，岸桥的上下框架的水平位移角也不超过0.3%，而框架结构在罕遇地震下的许用层间位移角一般为0.5%［16］。所以，为了将岸桥结构的水平变形限制在一个合理的范围内，并不需要直接定义一个难以准确量化的临界水平位移角，通过控制主体结构和斜撑的弹塑性变形，就能实现相同的目的。

表2 斜撑芯材的截面面积Tab.2 Cross-sectional area of core material in braces

图4 岸桥的水平位移角Fig.4 Lateral drift angle of container crane

4 优化结果验证

在OpenSees［17］中对得到的岸桥斜撑布置方案进行建模。采用桁架单元（Truss Element）对BRB支撑进行建模，采用基于纤维模型的分布塑性单元（Force-based Element）对箱型截面进行建模，同时考虑重力的二阶效应。材料的非线性采用双线性弹塑性模型进行描述，材料的屈服后刚度比取为0.01。对岸桥施加单调递增的水平侧向载荷（见图5），并通过“剪力-位移”曲线来分析岸桥的抗震能力。

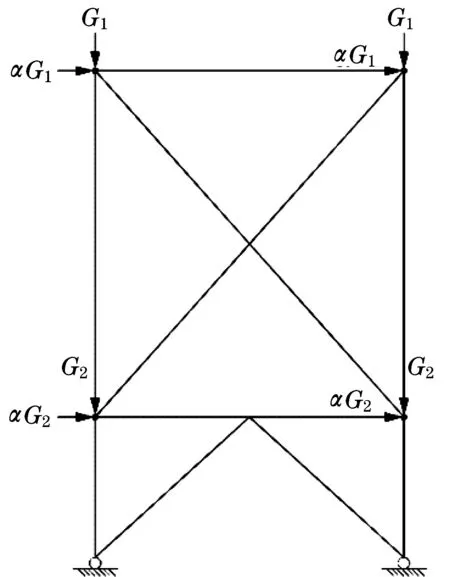
图5 岸桥的加载方式Fig.5 Load pattern of container crane

由图6可知，弹性拓扑优化和塑性拓扑优化得到的岸桥结构，在小震作用下水平位移基本相同。在地震烈度不超过12级（α≤0.8）时，弹性拓扑优化得到的岸桥结构能够保持弹性状态，而塑性拓扑优化得到的岸桥结构开始发生一定程度的塑性变形。随着许用塑性变形的增大，岸桥水平刚度降低，在大震作用下的塑性变形也逐渐变大。这个结果与优化数学模型中的支撑塑性变形条件相一致。由图7可知，当地震作用逐步增大时，岸桥中构件的屈服顺序依次是：下部门框的BRB支撑、上部门框的BRB支撑、下部门框的横梁-门腿连接处。也就是说，当地震输入能量较大时，BRB支撑会先于主体结构发生屈服，通过支撑的塑性变形，消耗一大部分地震输入能量，从而实现对主体结构的保护作用。同时，由图7可知，在岸桥的主体结构中，最容易发生塑性破坏的还是下部门框的门腿-横梁连接处。

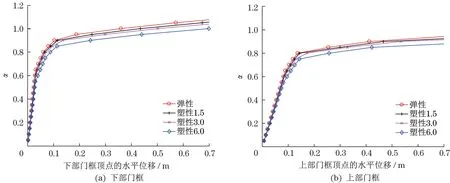
图6 岸桥的剪力-位移曲线Fig.6 Force-displacement curve for container crane

图7 构件的屈服次序（[Zc]=6.0[ε]，红色的线和圆圈表示屈服）Fig.7 Yielding sequence of components when[Zc]=6.0[ε]，red lines and dots denote yielding

5 结论

（1）所提出的岸桥斜撑抗震拓扑优化方法，能够确定斜撑的最优布置方案和最优截面尺寸，提高了斜撑布置的合理性，降低了抗震设计的成本。

（2）所提出的岸桥斜撑抗震拓扑优化方法，可以实现斜撑的弹性拓扑优化，也可以实现斜撑的塑性拓扑优化。对比弹性拓扑优化方法，塑性拓扑优化方法允许斜撑在给定地震条件下发生一定程度的塑性变形。

（3）将屈曲约束支撑应用于岸桥斜撑的抗震拓扑优化中，并让支撑在给定地震条件下发生一定程度的塑性变形小于让主体结构保持弹性变形，就可以实现用支撑的塑性变形消耗地震能量，进而保护主体结构。

（4）通过限制杆件的弹塑性变形可以间接实现对岸桥整体水平变形的控制，从而避免直接去定义岸桥门框的临界水平位移角。