试题“燕过留声” 方法“寻根觅源”——以数形结合方法运用于几道高考题为例

扬州大学数学科学学院(225002) 武 杰 陈建华

高考题具有代表性、示范性和“生长性”是人们的共识.教育专家希望它立意深远和背景丰富,反映课程标准的要求,发挥高考正向积极导向作用;一线教师期望它能关注学生对数学概念和定理的理解,引领高中数学教学的发展趋向,视它为教学的典型范例;高中生认为它是指挥棒和风向标.那么,如何合理利用高考数学题这一教学资源,发挥其潜在的教学价值呢? 本文以近年数学高考题为载体,探讨帮助学生深化对数形结合思想的理解.

一、以形解数,抽象问题直观化

“数”和“关系”都是抽象的产物,数学问题往往都是抽象的,这对问题的解决自然带来困难.对此,数学家斯蒂恩曾经说过,如果一个特定的问题可以转化为一个图形,那么,思路就整体地把握了问题,并且能创造性地思考问题.利用图形描述与分析问题中量的关系,可以化抽象为具体,减少问题的抽象性,有时还能避免代数法计算繁琐的问题,进而优化学生解决问题时的认知模式.

例1 (2019年高考江苏卷理科第14 题)设f(x),g(x)是定义在实数域R 上的两个周期函数,函数f(x)周期为4,g(x)的周期为2,且f(x)是奇函数,当x ∈(0,2]时,f(x)=而g(x) =其中k ＞0,若在区间(0,9]上,关于x的方程f(x)=g(x)有8 个不同的实数根,则k的取值范围是______.

分析本题主要考察分段函数、函数性质以及零点问题等相关知识点.这是有关“数”的问题,它需要求解出当两个函数相等且有8 个不同实数根时k的取值范围.审题和寻找解题思路时,许多同学会考虑将自变量取不同范围的解析式求解出来,但是由于f(x)既是周期函数,又是奇函数,所以在求解过程中既要时刻关注自变量的范围变化情况,又要防止弄错函数的奇偶性,稍不留神就可能前功尽弃.实际上,要写出具体解析式计算量较大,即使将f(x)解析式解出后,解题依旧难以进行下去,思维受阻.如果能根据问题情境的需要变换问题表征方式,用图形语言表征问题,借助图像表达思维和观点,就可以将方程根的问题转化为两个函数图像的交点个数问题.如图1 所示,在同一坐标系中画出两个函数的图像, 再利用函数的周期性与奇偶性观察其交点的个数,就能较为轻松地确定k的取值范围.

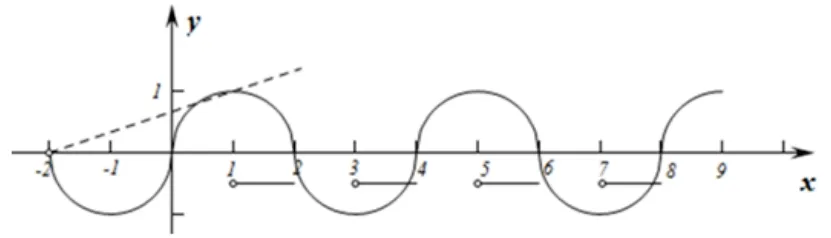
图1

解析根据题意,f(x) 在x ∈(0,2] 上是一个以(1,0)为圆心, 1 为半径的上半圆C,f(x) =g(x) 有8 个不同的实数根, 即函数y=f(x) 与y=g(x) 在区间(0,9]上有8 个不同的交点.由于f(x) 是奇函数, 且周期为4, 可以在同一坐标轴中画出f(x) 在x ∈(0,9] 上的图像和g(x) 的图像.从图中看出,g(x) =在区间(1,2]∪(3,4]∪(5,6]∪(7,8] 上与f(x) 函数图像共存在2个交点,所以当x ∈(0,1]∪(2,3]∪(4,5]∪(6,7]∪(8,9]时,g(x) =k(x+2)与f(x)函数图像有6 个交点,由图可知,当x ∈(2,3]∪(6,7]时,f(x)与g(x)图像无交点, 所以当x ∈(0,1]∪(4,5]∪(8,9]时,f(x)与g(x)图像存在6 个交点, 进一步将题目转化为区间上动线段与四分之一圆弧的位置关系问题.由f(x)与g(x)的周期性可知,当x ∈(0,1]时,g(x)过定点(−2,0)且f(x)与g(x)有两个交点,当直线g(x)=k(x+2)与半圆C相切时,d==1,解得k1=(负值舍去),当直线y=k(x+2)过点(1,1)时,k=所以,k的取值范围是

思考函数的零点问题是高中数学的重要内容之一,也是高考的热点.《课标(2017年版)》“学业质量水平”部分明确提出了“发现图形与数量的关系,探索图形的运动规律;能够掌握研究图形与数量之间关系的基本方法,借助图形性质探索数学规律,解决实际问题成数学问题[1]”的要求.如方程根的问题、存在性问题以及交点问题等都可以转化为零点的问题进行求解,函数零点个数可以转化为两个函数图像的交点个数问题,本质上就是执行课程标准的一种体现.熟悉基本初等函数的图像画法,能够根据问题给出的函数及其特性,较为准确地在同一坐标系中展示相关函数的图像是快捷解决此类问题的关键.

二、以数解形,复杂问题简单化

由于形的直观作用,数形结合思想方法运用中,人们往往看重的是“以形助数”,忽略“以数解形”.“以数解形”是指基于代数思维,通过数量运算来解决几何问题.特别是,当数学问题中条件是“形”而结论是“数”,或者是与数相关的量的情况下,可以根据数学问题的条件和结论之间的内在联系,分析它的代数意义,使数量关系与空间图形巧妙结合,缩小条件和结论间的矛盾差异,获得解题思路.

例2(2020年高考北京卷理科第13 题) 已知正方形ABCD的边长为2, 点P满足则

分析本题以向量为背景,题目简单明了,很多同学在碰到向量的问题都想通过图形的几何直观性来阐明向量之间的数量关系,然后通过向量运算解决问题.但由于向量位置在图中错综复杂,且从向量运算的三角形法则(或平行四边形法则)使用上看,很不方便,思路受阻.本题条件是几何意义下的图形与向量的和式,而求解的两个结论均为数,分别是向量的模长和向量的数量积.为了缩小条件与结论之间的差距,可以运用向量的数、形二重性,建立直角坐标系,将几何问题代数化,不仅加快了解题速度,还提高了解题的准确性.

解析如图2 所示, 以A为坐标原点, 建立坐标系.其中正方形的顶点坐标分别为A(0,0), B(2,0),C(2,2), D(0,2), 从而有:

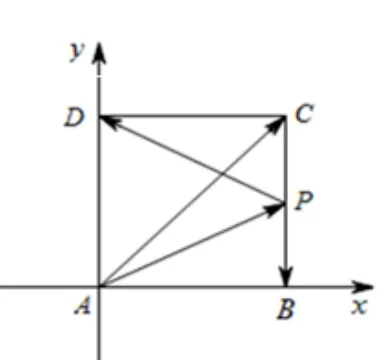
图2

设P(x,y), 即有= (x,y), 又因为所以解得所以有P(2,1), 则(0,−1), 故=(−2)×0+1×(−1)=−1.

类似的,有一道高考题,它是在直线和抛物线满足一定的关系条件下求直线的斜率问题.

例3(2018 高考全国III 卷理科第16 题)已知点M(−1,1)和抛物线C:y2= 4x,过C的焦点且斜率为k的直线与C交于A,B两点(如图3 所示), 若∠AMB=90◦,则k=____.

图3

分析如果聚焦于“形”,利用圆锥曲线的几何性质确定参数取值时, 发现图形太过于简单, 所含几何信息量较少, 无法构建相应的几何模型.考察抛物线与直线相交的问题,过抛物线焦点的直线斜率k满足以下的条件: 一是直线上的A,B两点在抛物线上,二是∠AMB= 90◦.其次,M点在抛物线的准线上且斜率为k的直线与抛物线有关, 由于∠AMB=90◦,可以将直线的斜率问题转化为向量的数量积问题,引入坐标,构建方程与函数的模型,将几何问题代数化,从“数”的角度寻求解决问题的突破口.

解析设A(x1,y1),B(x2,y2), 过椭圆焦点的直线方程为:y=k(x −1), 将直线方程与抛物线方程联立得:可得:k2x2−(2k2+4)x+k2=0.根据韦达定理可知:x1+x2=2+,x1x2=1,则y1+y2=y1y2=−4, 因为M(−1,1), 所以= (x2+1,y2−1),= (x1+1,y1−1).又因为∠AMB= 90◦,所以=0,即(x1+1)(x2+1)+(y1−1)(y2−1)=0,代入得:k2−4k+4=0,因此,k=2.

思考本题的求解关键是从“数”的角度出发,以“直角”作为切入点,引出数量积为零,建立等量关系,通过坐标运算进行转化,使问题的条件明晰化.一般地,从几何问题中抽取代数信息,巧借方程的思想求出坐标表达式,使向量的线性运算通过坐标来进行,实现向量运算的代数化,使几何问题转化为数量运算问题是一种重要而有效的解题思路.

三、形数互变,几何代数一体化

数与形是构成数学的两个基本对象,数学问题的解决经常会在“数”与“形”之间形成信息的相互转换中获得解题思路.形数互变的关键就在于理清楚“数”与“形”内在的联系,找准问题的关键点,再将代数与几何相互转化,二者结合,最终解决问题.

例4(2018 高考全国II 卷理科第19 题) 设抛物线C:y2= 4x的焦点为F, 过F且斜率为k(k ＞0) 的直线l与C交于A,B两点,|AB|=8.

(1)求l的方程;

(2)求过点A,B且与C的准线相切的圆的方程.

分析本题第一问求解不难, 第二问是主要考察与抛物线相切的圆的轨迹问题, 有一定的难度.首先,两点既在直线A,B上,也在抛物线图像上,又在所求的圆上,并且A,B两点的点坐标都满足抛物线解析式,这是“形”到“数”.其次,将直线与抛物线的解析式联立方程组,两点坐标就是所求的解,即为圆上的两个点,这是“数”向“形”.最后,找出“数”与“形”之间的连接点是求解第二问的关键.

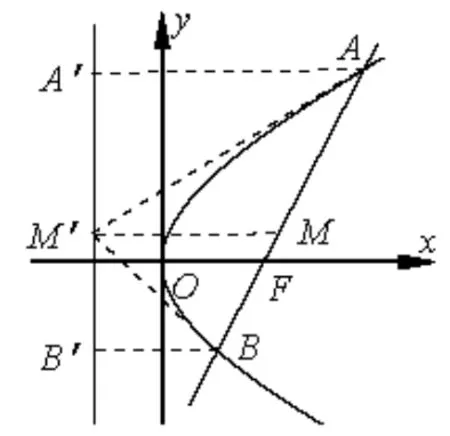
图4

联系圆心与圆上点之间的关系:AB为过抛物线焦点的焦点弦,取线段AB的中点为点M,过点A,B,M三点分别向抛物线的准线作垂线,垂足分别为A′,B′,M′,由梯形中位线可知,MM′=又根据直角三角形斜边上的中线等于斜边上的一半的逆定理可知,AM′⊥BM′,也就是说,以AB为直径的圆与抛物线的准线相切.这样就能得出过点A,B两点且与抛物线C的准线相切的圆的圆心为点M,直径为AB.

解析(1)直线l的方程为:y=x −1.

思考解决本问题有两个关键点: 一是通过AB的中点,作抛物线准线的垂线,从图形角度确定圆心所在位置以及圆的直径长度,二是根据A,B两点既满足抛物线方程,也满足圆的方程,从代数角度精确求出圆的方程.形与数的互变,使几何代数一体化,不仅可以将繁杂题目变得清晰明了,把握问题的关键点,又提高了解题效率,从而达到“1+1＞2”的效果.

数形结合是数学学习中一种重要的思想方法.数形结合思想是数量关系和图形性质之间的相互转化,“形”构成数学的直观化图形语言,“数”则是数学的抽象化符号语言,它们在一定条件下可以相互转化.通过以上分析可以发现,数形结合思想方法在高考题中涉及知识点非常广泛,高考数学题也越来越重视注重考察学生的创造性与发散性思维,在题目的设计上更具有开放性[2].因此,学生要学会建立形与数的联系,既要学会抽象问题直观化,利用几何图形描述问题,又要善于把几何问题代数化,优化代数运算优化解题.学会将几何直观与代数运算融合,通过形与数的结合,感悟数学知识之间的关联,加强对数学整体性的理解.