例谈不等式中的同构变形策略

山东省宁阳县复圣中学(271400) 张志刚

中学阶段, 同构式指变量不同而结构或形式相同的两个表达式.在诸多不等式(尤其是含双变量的不等式)问题中,经过整理变形使不等式呈现同构形式,然后构造函数,将隐含的不等关系凸显出来, 并结合函数的单调性解决问题,这种解题方法通常称为同构法.例如, 若F(x) ≤0 能等价变形为f[g(x)] ≤f[h(x)],借助f(x)的单调性,等价转化为g(x) ≤h(x)或g(x) ≥h(x).同构法的难点在于同构变形,下面以近年高考真题和模拟试题为例,阐述几种常见的同构变形策略.

1 策略一: 通过移项、添项、拆项等变形

结合已知条件, 对不等式进行移项、添项、拆项等变形,使得不等式两侧呈现相同结构,然后构造函数,利用函数的单调性实现问题的转化、解决.

例1(2020年高考全国II 卷理科第11 题)若2x −2y ＜3−x −3−y,则( )

A.ln(y −x+1)＞0 B.ln(y −x+1)＜0

C.ln|x −y|＞0 D.ln|x −y|＜0

解由2x −2y ＜3−x −3−y移项变形得2x −3−x ＜2y −3−y.设f(x)=2x −3−x,则f(x)＜f(y).易知f(x)是R 上的增函数,则x ＜y,从而y−x+1＞1,ln(y−x+1)＞0,故选A 项.

例2(2014年高考湖南卷文科第9 题) 若0＜x1＜x2＜1,则( )

A.ex2−ex1＞lnx2−lnx1B.ex2−ex1＜lnx2−lnx1

C.x2ex1＞x1ex2D.x2ex1＜x1ex2

解A 选项可变形为ex2−lnx2＞ex1−lnx1.为此,考查函数f(x)=ex −lnx,f′(x)=ex −,f′′(x)=ex+＞0,所以f′(x)在(0,+∞)上单调递增.又−e＜0且f′(1)=e−1＞0,所以存在x0∈,1),使得f′(x0)=0,并且f(x) 在(0,x0) 上单调递减, 在(x0,1) 上单调递增,故当0＜ x1＜ x2＜1 时,f(x1) = ex1−lnx1与f(x2) = ex2−lnx2的大小关系不能确定, 即无法判定选项A、B 是否成立.同理,C 选项可变形为为此,考查函数g(x)=,显然g(x)在(0,1)上单调递减, 故当0＜x1＜x2＜1 时,f(x1)＞f(x2), 即,故选项C 正确.

点评上述两例均为双变量不等式证明问题,解决策略是“分而治之”,即通过移项、简单的运算将地位同等的两变量x1,x2分离至不等式的两侧,化为相同的结构,然后构造函数,借助函数的单调性解决问题.

2 策略二: 通过放缩变形

对一些指对混合不等式问题,往往要借助已知条件或切线不等式(如lnx≤x −1(x ＞0),x+1 ≤ex)等工具合理放缩,创造同构形式,为构造函数奠定基础.

例3(2020年高考全国I 卷理科第12 题)若2a+log2a=4b+2log4b,则( )

A.a ＞2bB.a ＜2bC.a ＞b2D.a ＜b2

解由于4b+2log4b= 22b+log2b ＜22b+log2(2b),所以2a+log2a ＜22b+log2(2b).设f(x)=2x+log2x,则f(a)＜f(2b).又f(x)在(0,+∞)上单调递增,则a ＜2b,故选B 项.

例4(2012年高考浙江卷文科第10 题)设a ＞0,b ＞0,e 是自然对数的底数,则( )

A.若ea+2a=eb+3b,则a ＞b

B.若ea+2a=eb+3b,则a ＜b

C.若ea −2a=eb −3b,则a ＞b

D.若ea −2a=eb −3b,则a ＜b

解对于A、B 选项, 由于a ＞0,b ＞0, ea+ 2a=eb+ 3b ＞eb+ 2b, 设函数f(x) = ex+ 2x(x ＞0), 则f(a)＞f(b), 又f′(x) = ex+ 2＞0,f(x) 在(0,+∞) 上单调递增, 所以a ＞b, 故A 项正确, B 项错误.对于C、D选项, 由于b ＞0, ea −2a= eb −3b ＜eb −2b, 设函数g(x) = ex −2x(x ＞0),则g(a)＜g(b),又g′(x) = ex −2,g(x)在(0,ln 2)上单调递减,在(ln 2,+∞)上单调递增,所以无法确定a,b的大小关系.

点评本题借助已知条件a ＞0,b ＞0 合理放缩得:ea+2a ＞eb+2b和ea −2a ＜eb −2b,此时不等式两侧结构相同,就可以引入函数f(x)=ex+2x和g(x)=ex −2x,考查它们在(0,+∞)上的单调性即可.

3 策略三: 通过取对数运算变形

对于指数型不等式,特别是两个变量轮换出现时,可考虑对不等式实施取对数运算,将指数式转化为对数式,减少了运算量,降低了思维难度,然后将两个变量分离,往往会出现同构形式.

例5已经n ＞m ＞0,求证: (1+m)n ＞(1+n)m.

解因为n ＞m ＞0,(1+m)n ＞0,(1+n)m ＞0,所以只需证明ln(1+m)n ＞ln(1+n)m,即证nln(1+m)＞mln(1+n),亦即证明设f(x) =又f′(x) =易证明＜ln(x+1), 所 以f′(x)＜0, 从而f(x) 在(0,+∞) 上递减, 又n ＞m ＞0, 所以f(n)＜f(m), 即命题成立.

点评本题运用作差法等常规方法难度较大.由于本题是指数形式的不等式, 可考虑同时取自然对数, 然后分离m,n得构造函数(x ＞0),利用f(x)的单调性解决即可.

4 策略四: 通过恒等式b=alogab 代换变形

由对数的概念易得b=alogab(a ＞0,a ̸=1,b ＞0),特殊的a= elna,借助该式代换可将幂函数式等价变形为指数式,有利于同构式的创设.

例6(2018年高考全国I 卷文科第21 题) 已知函数f(x)=aex −lnx −1.

(1)设x= 2 是f(x)的极值点,求a,并求f(x)的单调区间; (2)证明: 当a≥时,f(x)≥0.

解(1)略.(2)当a≥时,f(x) ≥−lnx −1.只需证−lnx −1 ≥0, 即证ex≥e(lnx+1), 亦即证ex≥e ln(ex).不等式两侧同时乘以x(x ＞0) 得xex≥exln(ex),即证xex≥ln(ex)eln(ex).设g(x) =xex(x ＞0),则g(x) ≥g(ln(ex)).又g′(x) = ex(x+ 1)＞0,g(x) 在(0,+∞)上单调递增,所以x≥ln(ex),即证x≥lnx+1,上式显然成立,命题得证.

点评借助已知条件实施放缩, 将所证不等式变形为ex≥e ln(ex),再在不等式两边同时乘以x,此举看似“无中生有”、“毫无章法”,实则是基于不等式结构和谐性的考量.通过ex=eln(ex)的代换,转化为证明xex≥ln(ex)eln(ex),此时同构模型呼之欲出,引入函数g(x)=xex便顺理成章了.

例7(2020年新高考全国I 卷第21 题) 已知函数f(x)=aex−1−lnx+lna.

(1)当a=e 时,求曲线y=f(x)在点(1,f(1))处的切线与两坐标轴围成的三角形的面积;

(2)若f(x)≥1,求a的取值范围.

解(1)略.(2)f(x)的定义域是(0,+∞),若f(x)≥1,即aex−1−lnx+ lna≥1, 亦即elnaex−1−lnx+ lna≥1, 从而elna+x−1+ lna+x −1 ≥x+ lnx, 即不等式elna+x−1+ lna+x −1 ≥ elnx+ lnx在(0,+∞) 上恒成立.设g(x) = ex+x, 则g(lna+x −1) ≥g(lnx).又g′(x) = ex+ 1＞0,g(x) 在R上单调递增,所以lna+x −1 ≥lnx,从而lna≥lnx −x+1 在(0,+∞)上恒成立.设h(x) = lnx −x+1,h′(x) =当0＜x ＜1时,h′(x)＞0;当x ＞1 时,h′(x)＜0,故当x=1 时,h(x)有最大值0.所以lna≥0,得a≥1.

点评本题的关键是从不等式aex−1−lnx+lna≥1的结构入手,运用a= elna和x= elnx代换,变形为同构式elna+x−1+lna+x −1 ≥elnx+lnx,然后水到渠成地构造函数g(x)=ex+x,进行后续解答即可.

5 策略五: 应用恒等式b=loga ab 代换变形

类比恒等式b=alogab, 我们有b= loga ab(a ＞0,a ̸=1),特别的b= ln eb.利用该恒等式对不等式改造重组,可将幂函数式变形为对数式,同样有助于同构式的发掘.

例8已知不等式ex −aln(ax −a)+a ＞0(a ＞0)恒成立,求a的取值范围.

解由ax −a ＞0 及a ＞0 得x ＞1, 由题意得ex+a ＞ aln(ax −a), 不等式的两边同时乘以得+1＞lna+ln(x−1),即有−lna ＞ln(x−1)−1.在不等式的两边同时加上x有−lna+x ＞ln(x−1)+(x−1),即−lna+ln ex ＞ln(x −1)+(x −1),从而ln(x −1)+(x −1).设f(x)=lnx+x,则＞f(x −1),又f′(x) =+ 1＞0, 所以f(x) 在(0,∞) 上单调递增, 从而＞ x −1, 进而得恒成立.设g(x) =当x ∈(0,2) 时,g(x) 单调递增; 当x ∈(2,+∞) 时,g(x) 单调递减, 故g(x)max=g(2)=从而所以0＜a ＜e2.

点评本例解答过程中,首先通过参变分离得−lna ＞ln(x −1)−1,鉴于不等式右侧对数式不易改造,此时不等式两侧均加上x得−lna+x ＞ln(x −1)+(x −1),此时右侧代数式更和谐,规律性更强.接下来解决不等式左侧的结构变形问题,利用恒等式x=ln ex及对数的运算律将不等式变形为＞ln(x −1)+(x −1),此时,题设条件蕴含的规律已昭然若揭,跃然纸上.

例9已知函数f(x)=lnx −x+1,g(x)=axex −4x,其中a ＞0.求证:g(x)−2f(x)≥2(lna −ln 2).

证明

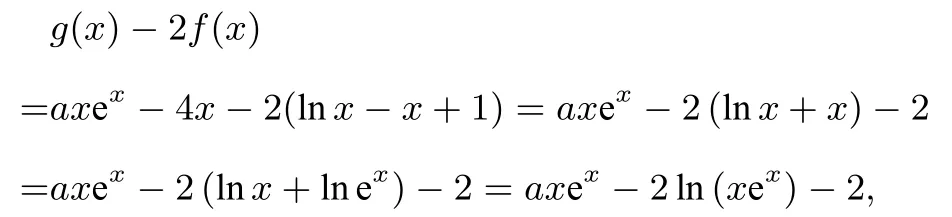
令t=xex,设h(t)=at−2 lnt−2,则h′(t)=(t ＞0),由a ＞0 易知h(t)在上单调递减;在上单调递增,所以h(t) ≥= 2(lna −ln 2),命题得证.

点评本例在对代数式g(x)−2f(x)整理变形中,关键是借助x= ln ex进行代换,使代数式结构更具统一性.通过换元,引入函数h(t)后,本质是证明同构式h(t) ≥成立,问题转化为讨论h(t)的最小值.

结合上述几例可知,同构变形需要深入审题,充分挖掘题设条件中可类比、联想的因素,促进思维迁移,从而选择恰当的变形策略,以便简捷、有效地解决问题.