基于广义Reed-Solomon码构造的两类量子MDS码
2021-03-17 09:33李建涛王伟伟
辽宁大学学报(自然科学版) 2021年1期
李建涛,王伟伟
(辽宁大学 数学院,辽宁 沈阳 110036)
0 引言
近年来,量子计算成为一个热门的话题.量子纠错码在量子通信和量子计算中扮演重要角色.构造一个具有好的参数的量子纠错码是非常重要的.近年来,许多研究者通过经典纠错码构造了大量的量子纠错码.
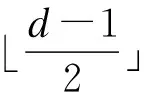

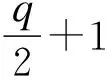
1 预备知识

1.1 Hermite自正交
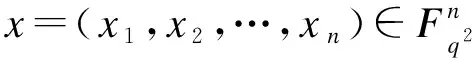
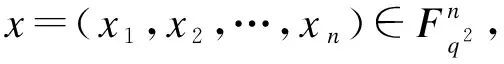
1.2 广义Reed-Solomon码

GRSk(a,v)={(v1f(a1),v2f(a2),…,vnf(an))|f(x)∈Fq2[x],degf(x) 称GRSk(a,v)为Fq2上的一个广义Reed-Solomon码GRSk(a,v).是一个参数为[n,k,n-k+1]q2的MDS码.事实上,GRSk(a,v)的生成矩阵为 下面的引理常被用来判断一个广义Reed-Solomon码是否是Hermite自正交的. 下面的结果现在经常用于构造新的量子MDS码. 定理 1[22]如果C是参数为[n,k,d]q2的线性码且C⊥H=C,则存在参数为[n,2k-n,≥d]q的量子码. 推论1[22]如果C是参数为[n,k,n-k+1]q2的经典Hermite自正交MDS码,则存在参数为[[n,n-2k,k+1]]q的量子MDS码. 为了得到本小节的结果,需要下面几个引理. (1) 综上,总有〈aqi+j,vq+1〉E=0. 为了得到本小节的结果,需要下面几个引理. (2) (3) AuT=(0,…,0)T, (4) 考虑方程组: BuT=(1,0,…,0)T. (5) 综上,总有〈aqi+j,vq+1〉E=0.
2 主要结果

2.1 第一类量子MDS码的构造
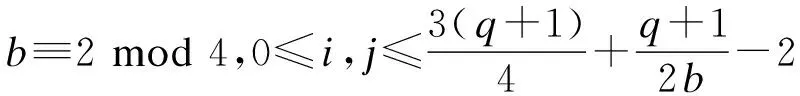



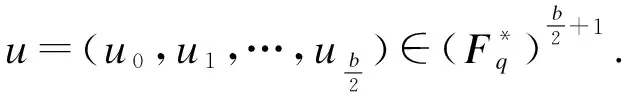




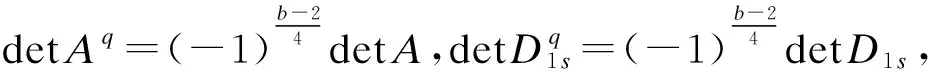



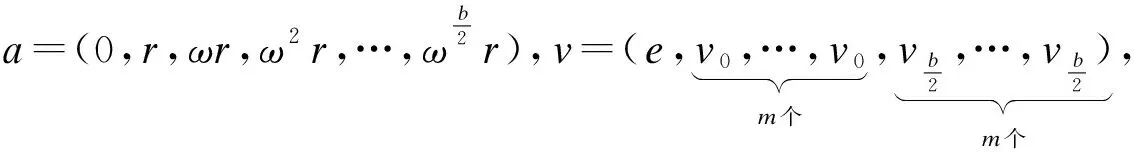



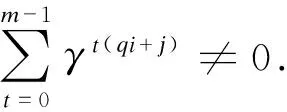
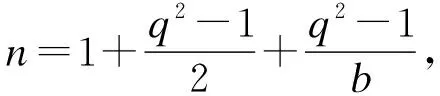
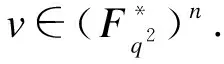

2.2 第二类量子MDS码的构造
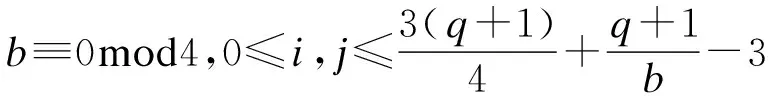

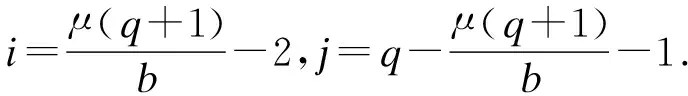
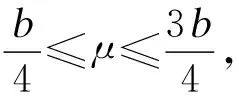

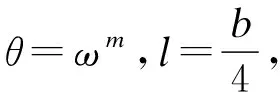


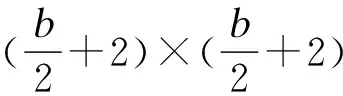






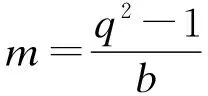


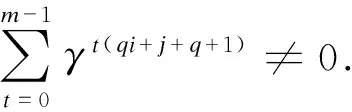

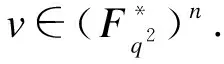

猜你喜欢
汉语世界(The World of Chinese)(2021年1期)2021-02-22
中学数学杂志(高中版)(2020年1期)2020-07-31
中学生数理化(高中版.高考数学)(2019年9期)2019-11-27
新生代(2019年4期)2019-11-13
中学生数理化(高中版.高考数学)(2019年9期)2019-09-27
中学生数理化(高中版.高二数学)(2018年11期)2018-11-29
数学学习与研究(2018年12期)2018-08-17
上海师范大学学报·自然科学版(2018年3期)2018-05-14
海峡影艺(2012年1期)2012-11-30
海峡影艺(2012年1期)2012-11-30

