小学低年段HPM拓展课一例
章颖

摘要:以古罗马数字1—20为素材,挖掘其思维内涵,在学生学完一年级的《11—20各数的认识》单元后,上一节拓展课,帮助学生感悟数学思想,发展数学思维。这节课的基本环节是:认识基本数字1、5、10;用“组合加”的方法创编2、3、4、6、7、8、9;用“换位减”的方法创编4、9;运用规则创编11—20;比较感受阿拉伯数字的简洁性。相关的教学启示有:数学史料的选择要有助于学生数学思维的发展;问题或任务的设计要有助于学生主动投入探究;认知冲突的创设要有助于学生思辨能力的发展。
关键词:数学史;数学思维;拓展课;古罗马数字
人教版小学数学一年级上册第五单元《6—10的认识和加减法》的两个《你知道吗?》栏目分别呈现了中国古代的算筹记数法和古埃及的象形数字记数法。前者在记数1—5时体现了累加的思想,在记数6—9时又体现了转换的思想;后者在记数1—9时都体现了累加的思想,在记数10时体现了转换的思想。
考虑到这两种记数法蕴含的数学思想较少,学习时需要的思考较浅,而且这两种记数法在现代生活中已经不再使用,笔者想到,可以古罗马数字1—20(Ⅰ、Ⅱ、Ⅲ、Ⅳ、Ⅴ、Ⅵ、Ⅶ、Ⅷ、Ⅸ、Ⅹ、Ⅺ、Ⅻ、、、ⅩⅤ、ⅩⅤⅠ、ⅩⅤⅠⅠ、ⅩⅤⅠⅠⅠ、ⅩⅠⅩ、ⅩⅩ)为素材,挖掘其思维内涵,上一节拓展课,帮助学生感悟数学思想,发展数学思维。《认识古罗马数字》一课可安排在学生学完一年级上册第六单元《11—20各数的认识》后。
一、数学史料解读
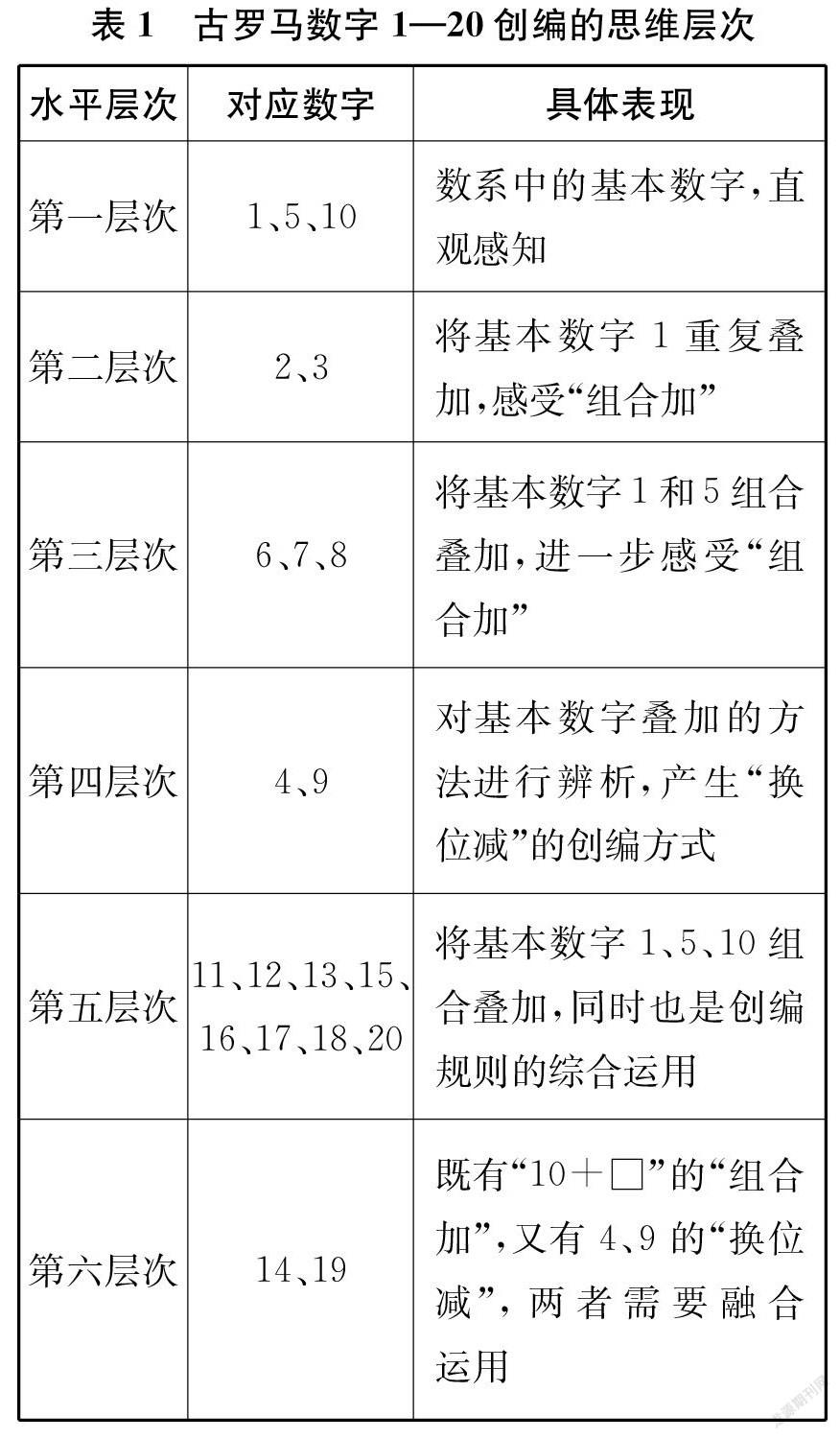
仔细分析古罗马数字1—20,不难发现不同数字创编的思维层次有所不同(详见下页表1)。其中,1、5、10是直接规定的基本数字,只需要了解,思维层次较低。从2、3两个
数字开始,就有了探究的价值。2、3是由基本数字Ⅰ累加得到的,6、7、8是由基本数字Ⅰ和Ⅴ组合而成的,它们遵循的是“小数在后是加”的规则。到了4和9,虽然也是两个基本数字的叠加组合,但遵循的是“小数在前是减”的规则。这两个规则可以让学生观察、发现、讨论、交流,最终达成共识。这就有了学生思辨的基础和空间。创编11—20时,则需要迁移运用之前的规则。其中,14、19的创编对学生来说难度尤为显著,因为它们不仅是三个基本数字的叠加组合,而且在“组合加”的过程中还用到了“换位减”。此外,单一数字创编后还要遵循统一性规则,使创编数字符合整个数系的规律。这也是需要学生思考、探究的地方。
综上可见,利用这一数学史素材,设计问题或任务引导学生思考和探究,可以让学生感受到数字创编过程中的关联性和统一性,进而认识到利用基本规则展开推理(根据基本思想进行思考)的重要价值。此外,通过与阿拉伯数字创编方法的对比,还可以让学生感受到阿拉伯数字的简洁性。
二、教学路径设计
基于古罗马数字创编的思维层次分析,本节课设计了如下的教学路径:
(1)创设情境,让学生了解古罗马数字中分别用Ⅰ、Ⅴ、Ⅹ代表1、5、10。
(2)让学生创编10以内的其他数字。在创编过程中,学生发现随着数字的增大,仅用Ⅰ叠加的方法很不方便,由此引入可以用不同的基本数字叠加。而4和6的创编,又引出数字组合的基本规则。
(3)让学生创编11—20。特别是在创编14、19的过程中,让学生通过讨论、交流进一步优化、补充数字创编规则。
(4)在进一步拓展中,将古罗马数字与阿拉伯数字对比,从而感受阿拉伯数字沿用至今的缘由——简洁性。
三、教学过程实施
(一)情境导入,认识基本数字1、5、10
师这单元我们学习了20以内数的认识。这些数字有一个统一的名字,叫作“阿拉伯数字”。今天,让我们穿越回古罗马,做一回古罗马人,创编古罗马时代的数字吧!
师(出示情境图)这是古罗马人的斗兽场。数一数,有几只猛兽?
生1只。
师(板书:Ⅰ)古罗马人用Ⅰ表示1。(出示情境图)现在有几只?
生5只。
师古罗马人用1只手表示5只动物。(做手势)瞧,它像哪个字母?
生V。
师(板书:Ⅴ)对,就是很像V但不是V的字母。(出示情境图)现在有几只?
生10只。
师古罗马人用2只手来表示10,但是他们还是想用1个字母来表示,他们就将一只手旋转了一下。(做手势)瞧,现在像什么字母?
生X。
师(板书:Ⅹ)同样地,这是一个很像X但不是X的字母。
[设计意图:通过情境导入,让学生直观了解古罗马人创造的数字与身体有密切联系,初步感受古罗马人的字母数字系统,为后续运用少量符号并通过它们不同个数的排列来表示不同的数做好铺垫。]
(二)合作探究,用“组合加”的方法创编2、3、4、6、7、8、9
师Ⅰ、Ⅴ、Ⅹ这三个字母就是古罗马数字中的基本数字,将它们组合起来能变出很多其他的数字。
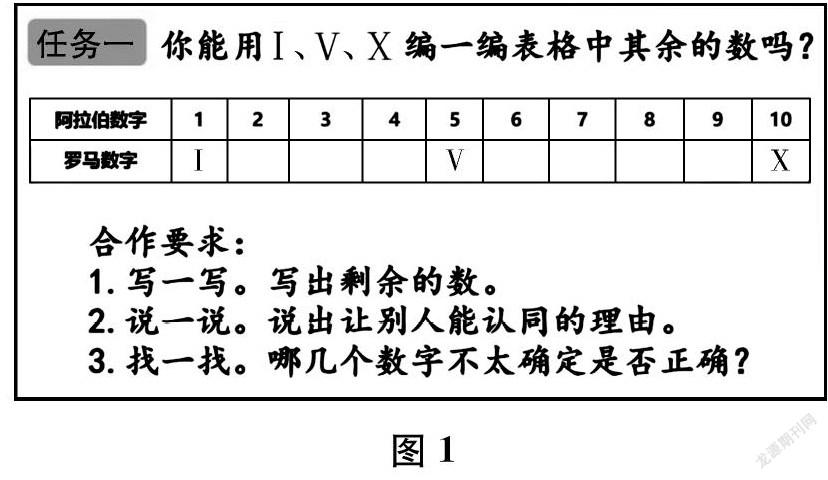
(教师出示任务一,见图1。学生合作探究。)
师 2、3、4这三个数,很多小组创编的都相同,你们为什么这样创编?
生 Ⅰ表示1,2里面有2个1,所以可以写成Ⅱ;3就是3个1,可以写成Ⅲ;4就可以写成ⅠⅠⅠⅠ。
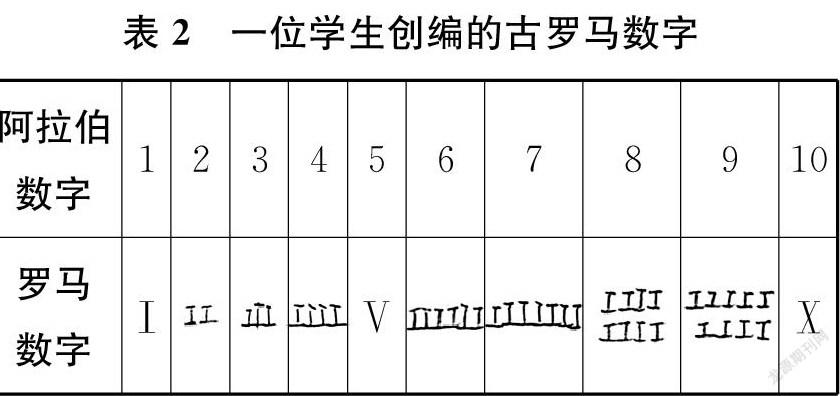
师 大家都是把Ⅰ一个一个叠加起来。看来,把基本数字叠加起来是创编数字的好方法。(出示表2)这位同学创编的罗马数字,你们觉得怎么样?
生 6—9太麻烦了。
师 有没有更简便的叠加办法?同桌讨论。
生 可以把Ⅴ和Ⅰ叠加起来。Ⅴ表示5,Ⅰ表示1,5+1=6,那6就可以写成Ⅵ。
师 除了6以外,还有哪些数字也能用这样的办法创编呢?
生 7—9。
師 请同桌一起修改6—9。
生 6是Ⅵ,就是5+1,那么,7可以写成Ⅶ,8可以写成Ⅷ,而9就可以写成ⅤⅠⅠⅠⅠ。
师 小朋友们真厉害,都学会了用叠加的方法创编数字!
[设计意图:创编2、3、4时,学生会自然想到直接用数字Ⅰ叠加。当数字超过5以后,学生会发现用“逐一计数”的方法越来越麻烦,从而产生“简化”的朦胧思想。通过讨论,学生发现可以将6—9都改写成“5+□”的形式,于是,用两个不同的基本数字叠加的想法也就油然而生。这样从繁到简自然过渡,学生能感觉到自己的想法和古人的想法是相通的,数学思想(思维)并不神秘。]
(三)迭代优化,用“换位减”的方法创编4、9
师 小朋友们把1—10的罗马数字都创编出来了。可是,在古罗马人的创编规则里, 还有这样一条:相同的基本数字可以连用,但不能超过3个。根据古罗马人的规则,你们觉得哪几个数字需要修改?
生 4和9。
师 先来看4,要想不连用4个Ⅰ,除了Ⅰ之外,还得用什么?
生 Ⅴ。
师 4=5-1,看来得用一个Ⅴ和一个Ⅰ。可是,6=5+1,也用了一个Ⅴ和一个Ⅰ,是Ⅵ。那么,4和6怎么区分呢?
生 可以把Ⅴ和Ⅰ换个位置,变成Ⅳ。
师 你们真会动脑筋!古罗马人也是这样,把小的数放在左边表示减,放在右边表示加。那么,9怎么创编呢?
生 9就是10-1,所以把Ⅰ放在Ⅹ的左边就可以了,就是Ⅸ。
师 既然你们创编出了9,那么,哪个数也能很快地创编出来?
生 11=10+1。把Ⅰ放在Ⅹ右边就可以了,就是Ⅺ。
师 比较一下前后创编的4和9,你能理解为什么基本数字连用不能超过3个吗?
生 连用超过3个不简洁。
生 连用超过3个数不清,容易看错。
[设计意图:新的创编规则激发了学生的认知冲突。学生观察、讨论4、6与5的关系后,发现只要调整Ⅰ的位置,就能区分5+1与5-1。進而,引导学生发现,新的创编规则让一些数字的写法得到了优化。]
(四)提炼迁移,运用规则创编11-20
师 刚才,我们创编10以内的数时,遵守了哪些规则?
生 要用基本数字:Ⅰ=1,Ⅴ=5,Ⅹ=10。
生 相同的基本数字可以连用,但不能超过3个。
生 小的数在左是减,在右是加。
师 现在请你们用这些规则来继续创编11-20。
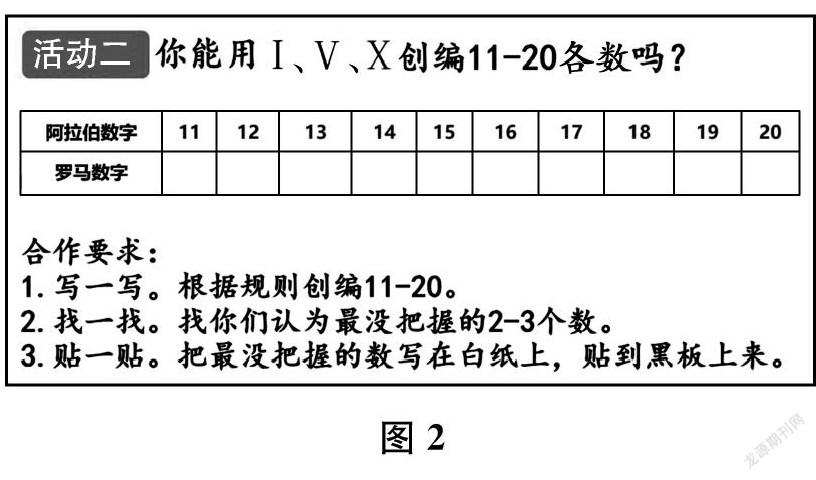
(教师出示任务二,见图2。学生合作探究。)
师 哪些数你们可以确定是对的?说明理由。
生 我们能确定11是Ⅺ,12是Ⅻ,13是。它们都是先写10,再分别加上1、2、3。
生 我们能确定的数是15、16、17、18,它们的写法和11、12、13相同,都是用10加上个位上的数。15是10+5,所以就是ⅩⅤ;16是10+6,而6是Ⅵ,因此就是ⅩⅤⅠ。按照这样的规律,我们知道17是ⅩⅤⅠⅠ,18是ⅩⅤⅠⅠⅠ。
生 我们还能确定20,20是两个10相加,就是ⅩⅩ。
师 那你们不太确定的就是14、19这两个数字吧?请把你们的写法贴到黑板上,大家一起来讨论。我们先贴14这个数。
(学生贴写法,见图3。)
师 你觉得哪种写法合理?说明理由。
生 我觉得ⅠⅤⅩ是对的,ⅠⅤⅩ可以看作ⅠⅤ和Ⅹ合起来,ⅠⅤ是4,Ⅹ是10,合起来是14。
生 我觉得ⅩⅠⅤ是对的,ⅩⅠⅤ可以看作Ⅹ和ⅠⅤ合起来,也是10+4=14。
师 大家觉得呢?
生 好像都有道理。
师 那我们再想一想之前的规则,或者把这两个数字放到11—20的表格中仔细观察。(稍停)现在,你觉得哪种写法更合适?
生 小的数在左是减,在右是加。ⅩⅠⅤ才是10+4,ⅠⅤⅩ应该是10-4。
生 我觉得ⅩⅠⅤ更合适,11是ⅩⅠ,12是ⅩⅠⅠ,13是ⅩⅠⅠⅠ,这3个数都是把Ⅹ放在前面,所以14也应该把Ⅹ放在前面。
师 非常好!你们都找到了依据,说出了道理。现在,你觉得19应该怎么写?
生 11—18都是把Ⅹ放在前面,变成10加几的样子,所以19也要把表示10的Ⅹ放在前面,应该是ⅩⅠⅩ。
师 对,古罗马人在创造数字时,就遵守了这样的统一规则。你们和他们一样, 很有智慧!
[设计意图:创编11—20,既是对规则的运用,又是对规则的进一步理解。此时,学生会在14、19这两个数上遇到困难,因为这两个数的创编既要用到4、9的“换位减”方法,又要将个位和十位上的数进行“组合加”,这对一年级的学生来说显得尤为困难。当学生觉得ⅠⅤⅩ和ⅩⅠⅤ都有道理,不知如何选择时,教师引导学生回想之前的规则或将这些数字放入数系中观察,这就从微观的角度拓展到宏观的角度,从而让学生感受到既要遵循创编的基本规律,也要保持数系的统一性。]
(五)拓展比较,感受阿拉伯数字的简洁性
师其实,随着数字变大,古罗马数字还会用到好多个基本数字呢!比如,表示3888,你们猜猜要用到多少个基本数字?
生 5个。
生 10个。
师 (课件出示3888的古罗马数字)一起来数一数。
生 啊!一共要用到15个基本数字。
师 你们有什么感觉?
生 太麻烦了。
师 那你们知道为什么现在我们的生活中只是偶尔用古罗马数字,而常用阿拉伯数字了吧?
生 还是阿拉伯数字方便。
师 是的,阿拉伯数字采用十进制记数法,只有10个基本数字,放在不同的数位就能表示不同的数,非常方便。
[设计意图:学习1—20的过程中,学生很难感受到古罗马数字的劣势,毕竟只要用到3个基本数字。但是,当数字变大后,古罗马数字的烦琐性就充分显示出来了。通过直观呈现的对比,让学生感受到阿拉伯数字的简洁性,理解为什么阿拉伯数字会流传至今,这也是数学史文化价值的充分体现。]
四、教学启示
(一)数学史料的选择要有助于学生数学思维的发展
数学史料极其丰富,每一份史料的价值也十分多元。作为一线教师,在数学史料的选择上,不仅要关注其文化导向功能,激发学生的数学学习兴趣,还要关注其蕴藏的数学思维价值,让学生的数学思维发展与数学文化学习更好地融通起来。
本节课,笔者通过对数学史料的细致解读与重新定位,发现1—20各数的创编规则及其难易程度不同。因此,教学中不能对每一个数字平均用力,否则,容易陷入知识的零散学习和技能的重复练习中。所以,本节课以“自主创编—提炼方法—运用方法—优化方法”为知识学习主线,并以“编—辨—辩”为思维发展主线,将数字创编的思维层次不断提升,从而促进学生的思维发展。
(二)问题或任务的设计要有助于学生主动投入探究
教学中,问题或任务能驱动学习真正发生,落实学生的主体地位。教师要设计探究性的问题或任务,激发学生的探究动力,驱动学生自主探究,进而合作交流,质疑问难,深入思考,发展思维。
本节课,笔者用“你能用Ⅰ、Ⅴ、Ⅹ创编1—10中其他的数吗?”和“你能用Ⅰ、Ⅴ、Ⅹ创编11—20各数吗?”这两个探究性问题(任务)串联、驱动。这两个问题看似重复,其实目的不同。前者主要是让学生通过自主探索、同伴讨论、展示交流,得出数字创编的基本方法。后者则是让学生迁移运用,并从单个数字创编的微观角度拓展到数系中数字规律统一的宏观角度,让学生的思维广度得到进一步拓展,思维深度得到进一步提升。虽然这两个问题的目的略有不同,但是它们的作用仍有相通之处:引发学生的高阶思维。这两个问题将可以直观呈现的知识以自主创编的形式加以转化,通过挑战学生的原有认知,激发学生的探究动力,并让探究的过程开放:不是随意写几个数字,而是需要抽象概括、逻辑推理、猜想验证、比较辨析等。这一过程能让学生的思维得到充分的发展。
(三)认知冲突的创设要有助于学生思辨能力的发展
思辨能力的发展对数学学习是至关重要的,它依赖于直觉思维,更依赖于逻辑分析。认知冲突的创设有助于让学生经历“观察分析、尝试解决、批判质疑、分析论证、反思优化”等过程,从而提升思辨能力。
本节课的第一个探究问题(任务)侧重于让学生经历“观察分析、尝试解决”的过程。在创编4、6时,引发了第一次认知冲突。学生通过思考,发现只要将Ⅰ和Ⅴ交换位置就能解决5+1和5-1的组合问题。第一次认知沖突让学生感受到思辨的意义,他们在对比辨析中发现,创编规则不只有“加”的方法,“减”也是一种很有效的方法。
本节课的第二个探究问题(任务)更侧重于利用认知冲突让学生经历“批判质疑、分析论证、反思优化”的过程。学生对14、19两个数的创编各有想法,而且对每种创编都能说出道理,但学生也知道只有一种创编是正确的。于是在这一过程中,“质疑”就自然而然地产生了。当从微观角度不能作出正确决断时,宏观的角度就成为必需。学生的思辨能力,就在比较辨析、讨论争辩的过程中得到了发展。
参考文献:
[1] 岳增成.数学史与小学数学教育:问题与对策[J].小学数学教师,2020(7/8).
[2] 汪晓勤.HPM视角下的小学数学教学[J].小学数学教师,2017(7/8).
[3] 李德虎,汪晓勤.HPM视角下的项目化数学教学设计——以“长方体直观图的画法”教学为例[J].中小学课堂教学研究,2021(11).
[4] 洪逸倩.小学低年级数学史融入数学教学的实践思考[J].教书育人,2021(34).
3118500316553

