初探“同课循环”式教研新模式
黄健华

[摘 要]“同课循环”式教研,强调在真实的情境中解决问题,注重现场观察、对等交流、措施调整,可盘活教师教研的积极性,是常规教研的有力手段。开展“同课循环”式教研,实现同课多练、同课异构、同课异形,通过教师观摩、反思、改进的循环交替促进教师专业素养的提高。
[关键词]同课循环;教研;异构
[中图分类号] G623.5[文献标识码] A[文章编号] 1007-9068(2021)05-0040-02
“同课循环”式教研模式,可盘活教师教研的积极性,是常规教研的有力手段,其强调在真实的情境中解决问题,注重现场观察、对等交流、措施调整。“同课循环”式教研主要有以下几种基本模式,现分别举例说明。
一、同课多练
同课多练是指同一位教师严格按照教研组选中的课题,多次在平行班施教,在评议交流反馈的基础上,不断改进完善,制订出最终教案。基本操作流程为:
一人同课多次重复试教,对于主讲教师大有裨益,但参与行动的不仅是主讲教师,所有教研组成员都要出谋划策、建言献策,记录主讲教师的课堂进程,对照反省,取长补短,共享教学成果。
【案例1】“口算两位数加、减两位数”的磨课
第一次执教:
反思点:这节课属于计算课还是解题课?这节课可圈可点的地方是重视培养学生采集信息的能力和解题能力,如设计问题“想要求解,需要什么数学信息作为前提?”“你觉得如何安排乘客登船较为周全?”(例题是规划邮轮的限座问题)。评课教师质疑:这是计算课还是解题课?如何妥善协调二者关系?主讲教师在综合评课教师所提出的意见后,当即表示立即整改,调整教学方向定位,将教学重点转移至口算上,并适度渗透解题策略。
第二次执教:
反思点:如何让学生掌握口算的方法?这节课值得褒扬的是重视培养学生的估算意识,如糅合情境设计提问:“預估一下,四个班能安排所有人就座吗?”“预估一下,一班、二班合并后能安排下所有座位吗?”“预估一下,三班、四班合并后能安排下所有座位吗?”让学生在具体情境中估算结果。本节课应突出算法多样性和个性化的特色,但主讲教师对于每道题只让一名学生起身作答,阐述算法,涉及面狭窄,不利于学生掌握算法。评课教师建议由扶到放,简政放权,让学生独立思考得出一定结论,然后反馈、展示和交流。要强化“算法比较”“另类算法”的意识,这样,学生才能开阔思路,在交流、切磋的基础上取长补短、去粗取精,优化计算方法。
本节课,学生有一闪光点。面对刁钻的问题“三班和四班满场,是否就此离场?有什么补救措施?”一女生当机立断:“三班和四班共有71人参会,只能安排68个客座,71-68=3,给3人单独安排一条快艇。”真是锦囊妙计,比课本上的乘船方案高明多了。女生落座后,还有多名学生不甘示弱,争相“献计”。遗憾的是教师没有给他们机会展示。
第三次执教:
反思点:缘何学生算法单一?二轮试教中,学生的算法呆板单调,只限于两种方式:在脑中虚构竖式;十位数加十位数,个位数加个位数,然后再合计。而对于教材中出现的第三种口算方法——把两位数加(减)两位数转化成两位数加(减)整十数和减一位数的分步计算,鲜有人提及。
评课教师建议让每个学生独立思考,催生学生的个性化算法;待学生独立思考后开展小组交流,最后集中展示交流成果,促成算法的多样化;高度重视学生原有的知识经验。
第四次执教:
反思点:怎么又还原成应用题解决课了?这次上课,主讲教师吸取教训,采纳建议,给了学生独立思考的时间,并充分调动学生知识经验来开展口算活动,因此算法多样性和个性化纷纷呈现,可惜仅在计算“23+31”时昙花一现,后续计算“32+39”“68-54”“32-14”时,学生的表现令人失望,教学重心又退回到解决问题上。
主讲教师辩称学生在口算“23+31”时多样化算法已生成,算理也阐述得很清晰,后面几题依葫芦画瓢即可,不必赘述。是不是全体学生都掌握了呢?评课教师重申:掌握算法不只是说说或者算一题就过关,必须通过交流来检验。其实在引导学生列出所有算式后,教师只需补述一句“你是怎么算的?”,将话题绑定在算法上,这节课就不会脱轨。
课堂永远是变化多端的。同一课题的四次执教活动落下帷幕,虽然最后没有做到十全十美,但是比起前几次却已是突飞猛进。
二、同课异构
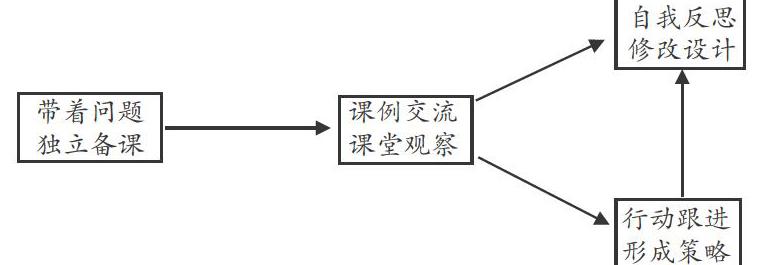
同课异构指同一年级、同一学科组紧密围绕一个有待解决的问题,以不同的构思上同一节课,相互批评指正,群策群力,探寻突破问题瓶颈的方案。基本操作流程为:
“课例交流,课堂观察”与“自我反思,修改设计”循环往复。年级组每位科任教师都要独立构思,互相观摩指教,不断修正完善。这样循环往复的过程,从不同角度、不同层次精研了课例。“行动跟进,形成策略”不仅强调对课本身的改善、优选和提升,更重视类比推理,回顾整理相关经验和教训,对施教决策做出全面反思与改进。
【案例2】三位教师“角的度量”的教学
主讲教师在教学了量角器的用法后,开始引导学生实践操作。活动中,绝大多数学生都能运用得法,主讲教师十分满意。就在这时,一个学生惊呼道:“老师,我的量角器断了,剩下的一个钝角无法测量,怎么办?”
第一位主讲教师:“用老师的量角器吧。”随即将量角器递送给学生。
第二位主讲教师:“遇见别人有困难时该怎么办?”“我已经量完了,用我的吧!”一个学生在教师的暗示和授意下仗义出手。教师当即褒奖他助人为乐的行为。
第三位主讲教师:“刘强的量角器断成两半,它还能量角吗?”将难题推给学生。“不行,小半块残缺的量角器没有中心点。”一个学生说道。“但是剩下的大半块残缺的量角器上存有中心点,刻度清晰可辨,应该不成问题。”另一个学生赶忙接话道。“可是刘强要量的角是钝角,那大半块残缺的量角器也不顶事呀。”一个学生辩驳道。“怎么解决问题呢?请大家商讨一下。”主讲教师话音一落,听课教师就会心地笑了。“先利用三角尺上的直角在钝角上‘辟出一个直角来,再利用那大半块残缺的量角器去测量余角的度数,所得度数加上90°,就是原来钝角的度数。”一个小组的学生提供了自己的方案。“不妨把这个钝角分割成两个锐角,再用那大半块残缺的量角器去量出它们的度数,再相加,就得到原来钝角的度数。”另一个小组也有独特方案。“老师,还可以画出这个钝角的补角,然后量出补角的度数,再用180°减去补角度数即可。”第一个小组的学生也不甘示弱……
面对教学生成,第三位主讲教师为什么没有简单直接地出借量角器,而是借题发挥,将学生的思维转接到探寻解决方案上,引导学生继续探究学习呢?这难道仅仅是一个计策吗?如果只是计策,也只能解燃眉之急,但始终不能成为一门艺术,更谈不上理念。
三、同课异形
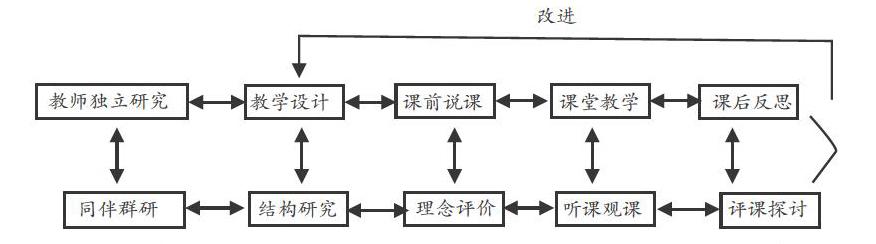
同课异形指同一位教师围绕同一节课完成设计、说课、教学、反思的全过程,同科教师进行跟踪评议,集体探究,寻找解题策略,改进教学措施。基本操作流程为:
“设计、说课、教学、反思”循环往复,不断修正调整,促进教师优化教学行为和磨炼教学技能。
【案例3】“两位数乘两位数”的教学
本堂课的教学设计,在导学案中以“我会学、我的疑问、我来迎战、我的获得”的形式呈现;教案中以“兴趣引入、算法探查、我来对战、我的获益”呼应。这堂课的基本构想是:试图在解题中探查算理,理顺解题的基本规程,再在解决具体问题时加以巩固夯实,即由具体到抽象,再由抽象到具体的循环认证。
主讲教师课后反思:对于学生在课堂中生成的错误,应该多让学生独立承担,在学生无力应对时,应适时提点,但学生还是一筹莫展,无话可说,此时教师是讲还是不讲?如果再继续提醒指教,就会延误时间,降低了教学效率。如果直接讲解,效率是提高了,可学生锻炼能力的机会就减少了。
集体研究开出的“药方”是:掌握好学生自主学习与教师指点之间的平衡。教师要在学生深入探究后仍迷惑不解时答疑,要在学生百思不得其解时答疑,要在学生智穷计短时答疑。
总之,对教师专业成长帮助最大的莫过于跟踪改进教学行为。“同课循环”式的教研,使教师观摩、反思、改进循环交替,极大地促进了教师专业素养的提高。
[ 参 考 文 献 ]
[1] 安丹诺.浅析同课异构视角下小学数学课堂的有效性[J].数学之友,2019(3).
[2] 马邹英.同课异构下的数学美学分析:以苏教版教材五年级上册“梯形面积的计算”的教学为例[J].小学教学参考,2018(26).
[3] 袁凤珍.从“树木”走向“森林”,整体把握分數的意义:“分数的意义”一课同课异构教学评析[J].小学数学教育,2018(10).
(责编 黄春香)

