土工格栅加筋路基土的松弛特性

李永靖，徐泽蔚，岳玮琦，郑晓明，张雨铭

(1.辽宁工程技术大学 土木工程学院，辽宁 阜新 123000；2.郑州航空工业管理学院 土木建筑学院，河南 郑州 450015)

0 引言

路基工程中铺设土工格栅是防止路基变形和提高其稳定性的有效途径。然而，在道路正常使用工况荷载下，格栅材料受力一般不超过其抗拉强度的30%～40%，但随着时间增长，黏弹性高聚物土工格栅材料会在长期荷载条件下发生蠕变，表现出流变特性，导致路基变形破坏。目前，研究土工格栅加筋路基土长期稳定性的内容较少，因此，探究土工格栅加筋路基土在长期车辆荷载条件下的流变特性对防止路基变形破坏有着更为重要的实际意义。

近几年，土工格栅常用高分子聚合物作为加筋材料，因其具有抗拉强度高、变形量大、韧性好等优点，在路基新建、维修及加宽改建等工程领域得到了较为广泛的应用[1-5]。格栅对路基土具有一定的嵌锁作用，提高了路基的抗剪能力，另外，格栅与路基土的摩擦作用提高了路基整体稳定性，也减少了路基的不均匀沉降[6-11]。国内外研究土工格栅加筋土的力学特性分为两种：一是分离式分析法，将格栅与土体相互作用看成是两种性质不同的材料，例如Nye 等[12]通过单调和循环直剪试验，研究了黏土与无纺土工布界面的剪切特性，并对界面刚度、阻尼比进行了分析；刘飞禹等[13]采用直剪仪对加筋土进行了循环剪切试验，研究了薄砂层不同厚度、不同循环剪切幅值和竖向应力对界面剪切特性的影响。可见，分离式分析法研究思路清晰直观，但格栅与土体的界面接触模型参数选取困难，计算结果偏差也很大。其二是整体式分析法，将格栅与土体相互作用等效为一种复合材料，采用统一的力学参数进行描述，例如SAWIKCI[14]假设格栅与土体间没有相对滑动，土体服从Mohr-Coulumb准则，建立了加筋土材料的塑性本构关系；S.M. Haeri等[15]对土工织物与砂试件的应力-应变关系进行了研究，获得了土工织物增强砂试样的强度峰值、轴向应变和韧性的变化规律；王磊等[16]将纤维格栅与土体假设为统一组合系统，分别采用修正剑桥模型和线弹性模型，建立了纤维加筋土的两相本构模型；苏立海等[17]基于三轴蠕变试验得到不同偏应力、不同加筋层数下土体的蠕变特性和加固机理。可见，整体式分析法成功避免了由格栅与土体接触界面分析不清所带来的复杂计算，且计算模型尺寸越大，所得结果越接近实际效果。

以上研究成果极大推动了土工格栅在加筋路基土等工程中的广泛应用。本研究以高分子聚合物土工格栅加筋土为研究对象，在整体式分析法基础上，根据格栅材料的黏弹特性与土体的非线性弹性本构模型，考虑土工格栅与土体的变形协调条件，推导出加筋土复合材料在路基一般受力情况下的松弛特性方程，并进行了三轴试验验证，开展了不同布筋方式下加筋土的受力变形特性及加筋土布筋优化方式的研究。

1 土工格栅筋材本构模型

为了研究土工格栅筋材在常温下的受力变形特性，对格栅筋材进行了低应力加载蠕变试验，并建立其应力应变关系的力学模型，试验所采用的土工格栅性能指标如表1所示。

表1 土工格栅规格与性能指标Tab.1 Specification and performance indicators of geogrid

1.1 土工格栅筋材蠕变加载试验

分别取土工格栅单根肋条抗拉强度的30%,40%,50%这3个荷载水平，并考虑在路基中的受力情况，在常温条件下(24 ℃左右)对单根格栅肋条进行蠕变加载试验，加载时间为1 000 h，加载参数见表2。

表2 土工格栅拉伸荷载Tab.2 Tensile load of geogrid

表2中的平均应力是将土工格栅肋条与网格间隙视为均匀连续体后换算得到的筋材截面应力值，试验得到筋材蠕变曲线如图1所示。

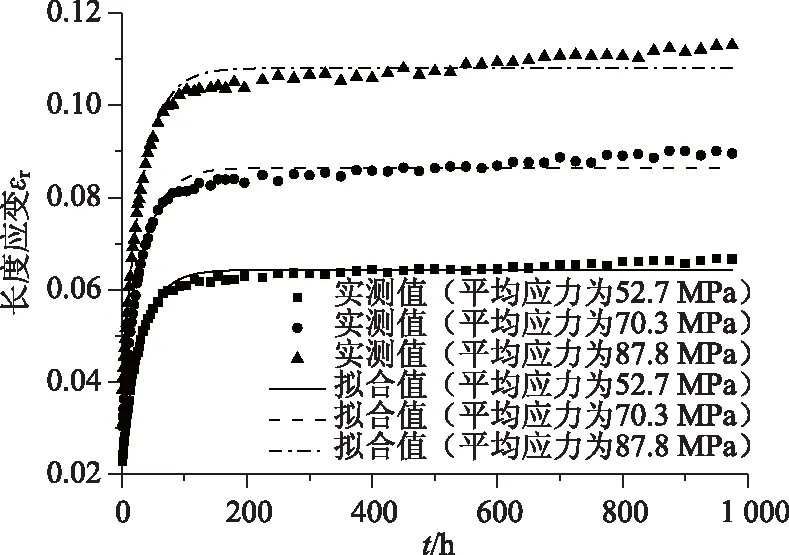
图1 土工格栅肋条拉伸蠕变Fig.1 Tensile creep of geogrid ribs

由图1可知，筋材蠕变速率开始上升较快，随后趋于稳定；格栅的拉伸长度应变值随荷载值的增大而增大，但蠕变曲线均在200 h左右进入稳态，说明蠕变收敛速度大致相同，属于衰减蠕变。

1.2 土工格栅筋材黏弹性本构模型

根据图1中土工格栅肋条蠕变试验呈现出的衰减蠕变特征，土工格栅筋材的受力变形特性可近似采用H-K体表示，如图2所示。

图2 三参数黏弹性模型蠕变曲线Fig.2 Three-parameter viscoelastic model creep curve

H-K体的应力应变关系见式(1)：

(1)

式中，σ，ε为土工格栅筋材的应力、应变；E1，E2为H-K体中两弹簧元件的刚度系数；η为H-K体中黏壶元件的黏滞系数；t为时间。

由图2可知，H-K体由一个弹簧元件E1和一个Kelvin体串联而成，当t=0时，即土工格栅在路基土中受瞬时应力时，弹簧元件E1产生瞬时弹性应变，而Kelvin体则由于黏壶的存在不产生瞬时应变，此时式(1)为：

(2)

若施加应力保持不变，在长期作用下(t→∞)，Kelvin体则随时间产生应变， H-K体即转变为弹簧元件E1与E2的串联体，最终使得土工格栅筋材的应变趋于稳定，此时式(1)表示为：

(3)

依据图1中蠕变试验结果，对式(1)中相关参数进行拟合求解，结果见表3。

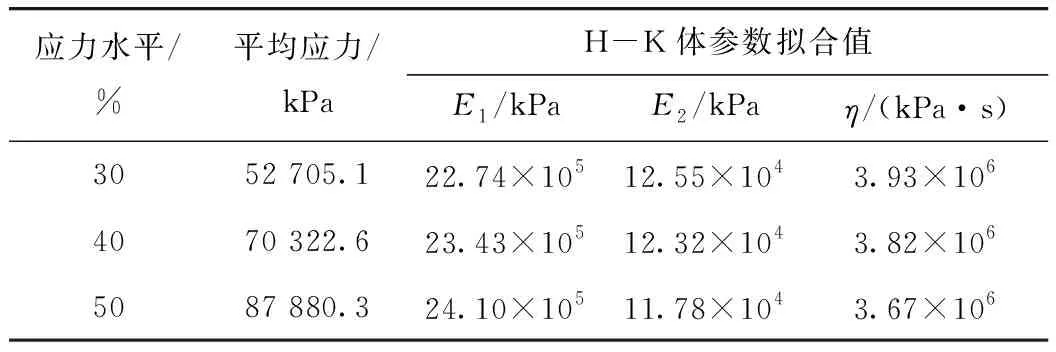
表3 黏弹性模型参数拟合值Tab.3 Parameter fitting values of viscoelastic model

2 加筋土的松弛特性

2.1 路基土的Duncan-Chang模型

Duncan-Chang模型结构简单，在路基土体荷载作用分析中有很强的适用性[18]。该模型能够反映土体加卸载情况下变形的非线性特征，且其模型参数可以通过三轴试验获得。在二维平面问题中，把主应力平面作为坐标面，设土体应力应变关系为双曲线形式，采用Duncan-Chang模型描述路基土在道路荷载工况下的应力应变关系见式(4)：

(4)

式中，σ1,σ3为土体的大、小主应力；ε1为大主应力方向土体应变；Ei为初始模量，即双曲线起始点切线斜率；(σ1-σ3)ult为主应力极限差，即应变趋于无限大的主应力差;a,b为邓肯张模型参数，试验常数。

2.2 加筋土本构模型建立

取层厚为λ的格栅筋材及两侧土体为加筋土材料受力单元进行分析，单元体高度为h，宽度为w，设格栅筋材与最大主应力方向的夹角为α0，如图3所示。

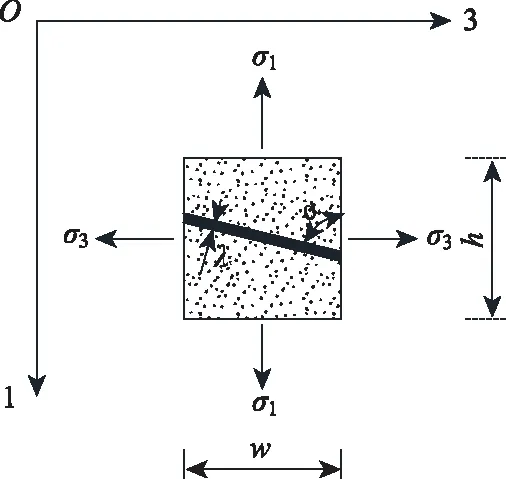
图3 土工格栅加筋土受力单元Fig.3 Stressed unit of geogrid reinforced soil

图3中，σ1，σ3为加筋土受力单元的大、小主应力。

沿筋材铺设方向，假设加筋土为均匀的各向异性体，且在路基加筋土中，设筋材应力应变符合式(1)黏弹性关系，路基土体符合式(4)非线弹性变形特性，即:

(5)

(6)

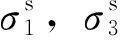
(7)

(8)

式中，n为加筋土受力单元中的含筋率；λ为土工格栅厚度；h为加筋土单元厚度，则由图3可知：

(9)

在图3受力单元中，假设筋材与土体之间不发生相对滑动，二者始终协调变形，则有：

(10)

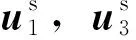
(εr+1)2=(1+ε1)2sin2α0+(1+ε3)2cos2α0,

(11)

式中，εr为格栅筋材轴向应变；ε1，ε3为加筋土的大、小主应变。由式(11)可得，当α0=0时，εr=ε1；当α0=π/2时，εr=ε3，即当土工格栅铺设方向分别与主应力平行、垂直时，筋材的轴向应变分别等于单元体的大、小主应变，这与实际情况也相符合。

将式(7)、(8)相减，可得:

(12)

将式(5)、(6)代入式(12)，可得:

(13)

式中，εr可由式(11)求得，即

(14)

以上是运用整体式分析法，将土工格栅筋材与两侧土体视为同一种复合材料，认为路基土体服从Duncan-Chang模型，建立了加筋土材料的黏弹性本构模型，如式(13)所示，此式能够反映平面应变状态下复合材料受偏应力随时间的变化情况，因此，式(13)即为土工格栅加筋路基土体的松弛方程。需要说明的是，该方程仅适用于单层加筋的路基土体复合材料，对于多层布筋情况下，土工格栅材料的参数E1，E2与η，需进行多肋土工格栅蠕变试验对式(1)拟合求解，或利用H-K体的并联关系进行重新计算。

3 加筋土松弛特性试验验证

3.1 试验设计

由式(13)可知，加筋土的松弛特性与土体和筋材的材料性质有关。为了分析加筋土的黏弹性松弛特性，制作了无加筋土体试件进行三轴试验，分别在100，200，300，400 kPa这4种围压水平下，测得Duncan-Chang模型中的参数a，b结果如表4所示。

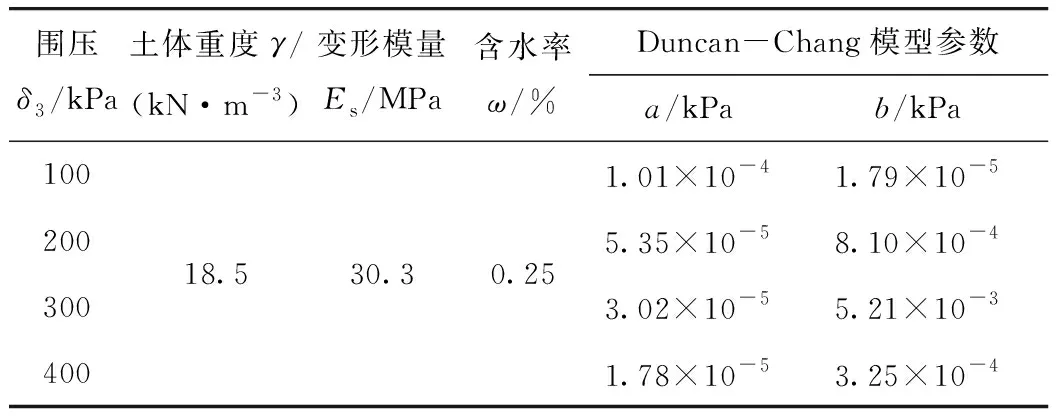
表4 Duncan-Chang模型参数拟合值Tab.4 Parameter fitting values of Duncan-Chang model

采用上述参数的土样和土工格栅(表1)制作加筋土试件，取100，200，300，400 kPa这4种围压水平对土工格栅加筋土试件进行流变加载。采用英国制造的GDS多功能三轴仪进行流变试验，该三轴试验系统包括软件、Bishop & Wesley型液压应力路径三轴压力室、标准型压力控制器(STDTTS)和高级型压力控制器(ADVTTS)。测定试件的松弛特性试验方法如下：(1)施加固结荷载对试样进行排水固结，直至稳定；(2)选择GDS三轴仪中的高级加载模块，按一定的剪切速率对试样进行加载，剪应力q=σ1-σ3随应变值ε1的增加而加大,当剪应力q达到峰值强度的80%～90%时停止剪切；(3)选择高级加载模块中的“围压保持不变,反压为0，应变保持不变”的加载方案持续加载200 h。

3.2 试验规律分析

将采集到的试验数据，绘制剪应力q=σ1-σ3随时间的变化规律，并与式(13)计算出的理论值进行对比分析，结果如图4所示。

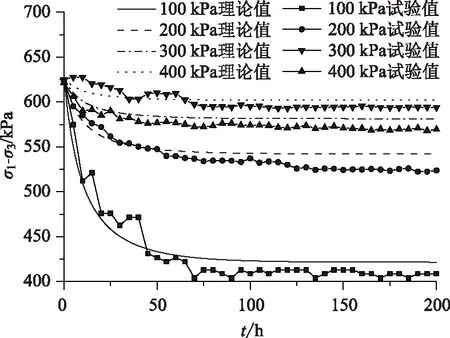
图4 不同围压下加筋土松弛曲线Fig.4 Relaxation curves of reinforced soil under different confining pressures

由图4可知，试件在不同围压下，剪应力均随时间增长而减小，50 h前降幅较大，50 h后缓慢趋于稳定；由图4还可看出，t=0时的剪应力初始值均为627.5 kPa，随着时间的增长，松弛速率和松弛幅度均随围压增大而减小，200 h时，围压为100，200，300，400 kPa对应的松弛幅度分别为35.2%，16.2%，8.9%，5.4%；同时，根据式(13)计算的理论松弛曲线也绘制于图4中，与试验得到的松弛曲线对比可知，二者趋势相同，证明了式(13)能够反映加筋土材料的松弛特性。

4 加筋土松弛特性影响因素

分析式(13)可知，加筋土的松弛特性不仅与围压有关，还受材料的主应变ε1、格栅铺设角度α0及含筋率n的影响，具体分析如下。

4.1 格栅铺设角度α0的影响

制作格栅铺设角度α0为π/2，π/3，π/4，π/6的加筋土试件，保持围压100 kPa和加筋土轴向应变8.0%不变，按3.1节中所述松弛特性试验方法进行流变试验，得到试件剪应力随时间的变化曲线，并与式(13)计算的理论松弛曲线进行对比分析，二者趋势相同，结果如图5所示。

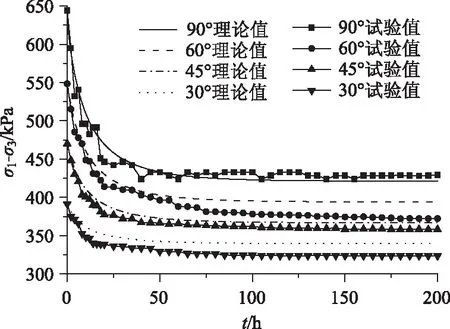
图5 不同土工格栅铺设角度加筋土松弛曲线Fig.5 Relaxation curves of reinforced soil under different geogrid laying angles

从图5中可以看出，在相同围压下，随着格栅铺设角度α0的降低，试件达到相同轴向应变时的初始剪应力降低，分别为627.5，548.3，470.1，391.2 kPa;200 h后的松弛幅度也随之降低，分别为35.2%，32.1%，23.8%，17.3%。在路基加宽实际工程中，根据路基受力特点，越靠近路基中央，最大主应力方向越近似为垂直方向，水平铺设土工格栅可充分发挥加筋土的抗剪性能；而靠近路基边缘，最大主应力方向发生一定的偏转，可适当调整土工格栅的铺设方向来增大加筋土的抗剪能力，试验结果与实际情况相符。

4.2 含筋率n的影响

设格栅铺设角度α0为π/2，制作含筋率n为0.008，0.012，0.02，0.03的加筋土试件，保持围压100 kPa和加筋土轴向应变8.0%不变，按3.1节中所述松弛特性试验方法进行流变试验，得到试件剪应力随时间的变化曲线，并与式(13)计算的理论松弛曲线进行对比分析，二者趋势相同，结果如图6所示。

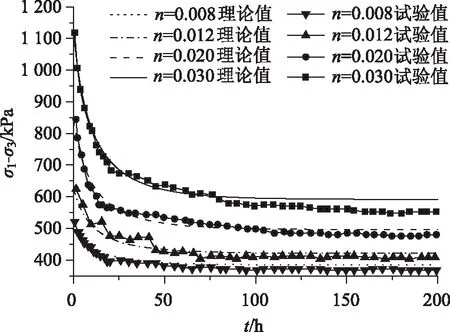
图6 不同含筋率加筋土松弛曲线Fig.6 Relaxation curves of reinforced soil under different geogrid reinforcement ratios

从图6中看出，随着加筋土含筋率的增大，试件达到相同轴向应变时的初始剪应力增大，分别为521.2，627.5，843.0，1 120.6 kPa，200 h后的松弛幅度也随之增大，分别为28.0%，35.2%，43.1%，50.4%。试验可知，增加路基土中的土工格栅含量，可有效提高加筋土的抗剪性能，但较高的含筋率会造成后期松弛幅度较大，导致路基后期承载能力大幅下降，路基变形严重，因此，在路基加宽实际工程中，不能依靠增加土工格栅含量来增强路基承载力，需要根据路基实际荷载情况确定出合适的加筋土含筋率。

5 结论

(1)根据格栅筋材的黏弹性本构模型与路基土体的Duncan-Chang非线弹性本构模型，建立了加筋土复合材料的松弛方程。试验验证了所建立的松弛方程能够很好地描述加筋土的松弛特性及各因素的影响规律。

(2)流变加载试验表明，在初始剪应力相同的情况下，加筋土试件的松弛速率与松弛幅度均随围压增大而减小，松弛稳定时间也相应缩短。

(3)在相同围压下，随着格栅铺设角度的降低，试件达到相同轴向应变时的初始剪应力降低，200 h后的松弛幅度也随之降低。

(4)在相同围压下，保持格栅铺设角度不变，随着加筋土含筋率的增大，试件达到相同轴向应变时的初始剪应力增大，200 h后的松弛幅度也随之增大。