基于Fast-ICA算法的改进EEMD算法在桥梁工程中的运用

罗烨钶，陈永高，李升才

(1.浙江工业职业技术学院，浙江 绍兴 312000；2.华侨大学 土木工程学院，福建 泉州 362000)

0 引言

桥梁在正常使用过程中，会受到外部荷载、有害物质以及自身材料老化等因素的影响，而发生不同程度的损伤[1]和抗力衰减。对于实际桥梁结构而言，当其结构自身发生一定的损伤时，其对应的模态参数会发生不同程度的变化；根据这一特性，有专家提出可通过监测桥梁结构自身模态参数[2]的变化情况来间接评估其整体状态和损伤状况。现阶段，以振动分析为基础的桥梁结构健康状态[3]评估方法逐渐受到人们的重视，模态参数识别作为振动分析的关键问题之一，还需进一步完善。模态参数识别是指：对结构的振动信号进行动力特性参数的识别，以得到结构的频率、振型以及阻尼比。实际桥梁结构中，为了精确地识别其模态参数值，首先应对结构自身的响应信号进行信号分解和重构，其次再对重构信号进行模态参数辨识。现阶段，常用的信号分解算法是集合经验模态分解算法(Ensemble Empirical Mode Decomposition, EEMD)[4]；常用的模态参数识别算法是随机子空间算法(Stochastic Subspace Identification, SSI)[5]。随着EEMD算法的普及，其缺陷也越来越明显，其主要缺陷是分解所得本征模态函数(Intrinsic Mode Function, IMF)间存在模态混叠现象[6]和对于有效本征模态函数的定义没有统一的标准。

鉴于此，本研究针对EEMD算法存在的不足提出将夹角余弦法用于筛选有效IMF分量，同时将盲源分离算法中的Fast-ICA算法[7]嵌入EEMD分解算法中以得到一种新的信号分解算法，并验证该算法运用于模拟信号的可行性；将所提改进算法和EEMD算法分别运用于实测桥梁信号中，并采用随机子空间算法识别重构信号以获得模态参数值，对比所得模态结果与理论值以验证识别结果的可靠性。

1 盲源分离算法的模型建立

盲源分离算法[8]的主要特点在于能够依据输出信号来估计推导出输入信号和各组成信号，分离的过程属于一种求逆的过程。以下介绍分离算法的主要步骤，以便将其与EEMD算法进行结合以实现系统信号的自适应分解。

建立盲源分离模型[9]的步骤：

(1)假设源信号为一组n维的信号矩阵，即X=[x1,x2,x3,…,xn]；

(2)假定混合矩阵为A，因结构系统处于环境条件下，即A为未知矩阵；

(3)源信号X=[x1,x2,x3,…,xn]在产生或传输过程中会与混合矩阵相作用，得到混合后的信号S=[s1,s2,s3,…,sn]，该S为传感器在实际现场所测得的结构振动信号，属于已知信号矩阵,表示如下：

S=X·A。

(1)

(4)对于式(1)，仅是知道混合信号S，还无法求解出源信号矩阵X，需要求解出混合矩阵A的逆矩阵A-，才能求解出源信号矩阵X；

(5)假定W=A-，则可得Y=W·S=W·X·A，其中Y为盲源分离算法的分离结果，可见，求解W是该算法的本质目的。

综合上述步骤，可知盲源分离模型的建立流程图如图1所示。

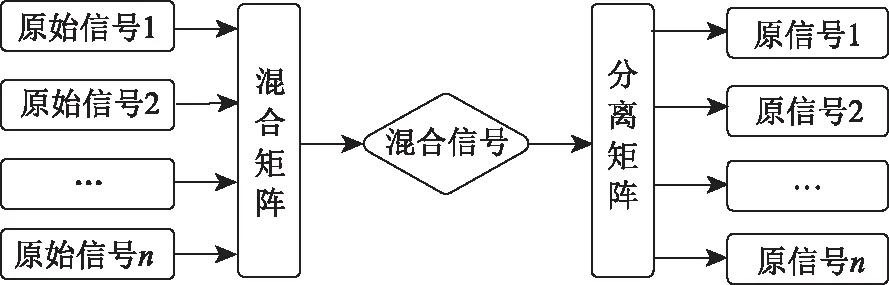
图1 盲源分离模型流程图Fig.1 Flowchart of blind source separation model

2 Fast-ICA算法

Fast-ICA算法由芬兰赫尔辛基大学Hyvärinen[10]等人提出，其基本原理是通过快速迭代比较来求解出最佳的分离矩阵。同时该算法为了保证各混合信号间不具相关性，对混合信号进行前期处理，即对混合信号进行中心化处理和白化处理，进而保证分离结果的准确性。

Fast-ICA算法主要分为信号的前期处理和算法迭代；以下分析这两大步骤的具体流程。

2.1 前期处理-中心化处理

数据中心化处理能够保证各样本的均值为0，且不会改变样本中数据点间的相互位置，同时也不会改变变量间的相关性。对数据进行中心化处理的主要目的在于使得采集到的混合矩阵各分量成为零均值向量，简化算法步骤。

数据的中心化处理[11]是指平移变换，公式为：

(2)

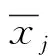
2.2 前期处理-白化处理

白化处理的主要目的在于保证混合信号S=[s1,s2,s3,…,sn]中各分量之间不具相关性，得到白化后的混合信号，简化Fast-ICA算法的过程。其原理是将S=[s1,s2,s3,…,sn]或者噪声的协方差矩阵进行对角化处理。

进行白化处理时，需满足如下约束条件：

(1)独立成分之间不具相关性；

(2)独立成分不满足高斯分布；

(3)混合矩阵需为方阵，若不满足则需对S=[s1,s2,s3,…,sn]做白化处理，以便降低其组成的矩阵维数。

对S=[s1,s2,s3,…,sn]进行白化处理得到新矩阵Snew：

Snew=U·S，

(3)

式中，U为白化矩阵，Snew中各分量具有二阶不相关性，且具有单位方差。对S=[s1,s2,s3,…,sn]的协方差进行特征值分解，可求得白化矩阵U。

U=VD-1/2VT，

(4)

式中，V为分解变量：求解S=[s1,s2,s3,…,sn]的协方差矩阵E[SST]的特征向量，组成正交矩阵以获得分解变量V；D为对角阵，由各个特征向量所对应的特征值组成。

由式(3)和式(4)可得经白化处后的信号：

Snew=U·S=VD-1/2VT·S。

(5)

2.3 算法迭代

Fast_ICA算法是在独立成分分析(Independent Component Analysis，ICA)算法[12]的基础上改进所得，实质上属于一种快速定点ICA算法，它在多次迭代对比中能找到一个单位矢量，使得wTs达到最大值。

定点算法迭代公式为：

wi(k+1)=E[sig(wi(k)T)si]-

E[g(wi(k)T)si]wi(k)，

(6)

式中g为一个非线性函数。

具体迭代步骤如下：

Step 1：假定i=1。

Step 2：随机选择范数为1的初始矢量w(0)，并假定k=1。

Step 3：采用式(6)。

Step 4：假定wi(k)=wi(k)‖wi(k)‖。

(7)

每对wi(k)完成一次迭代，则需对其进行一次归一化处理[13]。归一化处理的理由在于：Fast-ICA算法对信号的能量要求较高，所以必须通过归一化处理来保证信号具有足够的能量来完成算法。

Step 5：|wi(k)Twi(k-1)|收敛于1，则整个算法结束运算，并输出矢量wi(k)；否则令k=k+1，返回执行(3)然后继续迭代。

Step 6：若迭代后i的值等于源信号个数，则返回执行(2)。直至把所有的源信号分离出来。

基于上述步骤，便能通过循环迭代估算出各个独立分量。为避免同一个独立分量被反复迭代，这里需要在Step 4中加入一个正交投影，转换为公式：

(8)

Fast_ICA算法的流程图如图2所示。

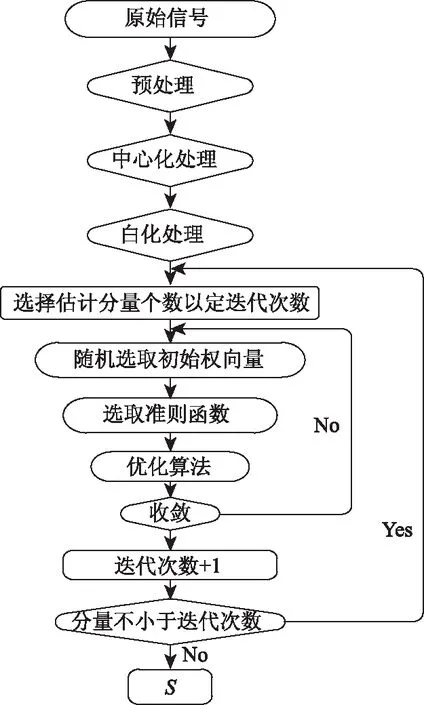
图2 Fast-ICA算法流程图Fig.2 Flowchart of Fast-ICA algorithm

3 EEMD算法的改进

EEMD算法是以EMD算法[14]为基础改进而得，其原理为：将等幅值的随机白噪声添加到原始信号中，以改变信号内部极点的分布情况，使得各极点的分布更加均匀，进而避免高频分量影响最终的分解结果；同时基于对所有结果取均值的方式来消除本征模态函数分量中的白噪声。

随着该算法的广泛运用，不少学者[15]发现所得IMF分量间会发生模态混叠现象，即所得各IMF分量间会存在信息的重叠。鉴于此，本研究先将盲源分离算法中的Fast-ICA算法融入到EEMD算法中以避免模态混叠现象的发生。

3.1 EEMD算法的实现步骤

Step1：将N个不同的Gaussian白噪声wi(t)(i=1,2,…,N)加入原始信号x(t)中得到xi(t)，即：

xi(t)=x(t)+wi(t)，

i=1, 2,…,N。

(9)

Step2：对xi(t)进行EMD分解得到IMFij和残余项rij，j代表每次EMD分解后IMF的个数，即：

j=1, 2,…,n。

Step3：对所有IMF取平均，求得最终的IMF，即：

(11)

3.2 IMF分量的有效筛选

根据3.1节EEMD算法流程可知，对原始信号进行EEMD分解可得到一系列IMF分量。就如何辨识所得IMF分量是否为有效分量，没有统一的处理方式；基于此，本研究引入夹角余弦法[16]对IMF分量进行筛选，具体实现过程如下：

Step1：考虑到各IMFj(j=1,2,…,n)分量和原始信号x(t)间的数据可能存在量纲差异，所以需要分别对其进行数据归一化处理，以保证各组数据间具有可比性，计算公式如下：

(12)

式中，IMFj,min和IMFj,max分别代表IMFj的最小值和最大值；x(t)min和x(t)max分别代表x(t)的最小值和最大值。

(13)

3.3 Fast_ ICA算法的应用

基于3.1节和3.2节，可实现对原始信号x(t)信号分解，并获得有效IMF分量。基于此，可通过如下算法流程将Fast_ICA算法融入到EEMD算法中以避免IMF分量间信息发生重叠现象。

Step1：基于2.1节所提算法，对有效IMFi(i=1,2,…,m)进行中心化处理，其中m为有效IMF分量的个数；

Step2：基于2.2节所提算法，对step1所得IMFi(i=1,2,…,m)进行白化处理；

Step3：基于2.3节所提算法，对step2所得IMFi(i=1,2,…,m)进行算法迭代，求解出最终的有效IMF；

Step4：利用式(14)对筛选出的有效IMF分量进行叠加以得到重构的有效信号X(t)；

(14)

基于夹角余弦法和Fast_ICA算法的改进EEMD算法流程图如下：

图3 改进EEMD算法Fig.3 Improved EEMD algorithm

4 仿真信号验证

仿真信号由1 Hz和0.1 Hz的正弦信号叠加0.5 Hz 的余弦信号，并叠加噪声水平约为10%的随机噪声组成：

s(t)=1.5sin(2πt+π/8)+cos(πt+π/4)+

0.5sin(0.2πt+π/5)+10rand。

叠加信号共20 s，采样频率为100 Hz，即2 000个测试点，叠加信号时程曲线图如图4所示。

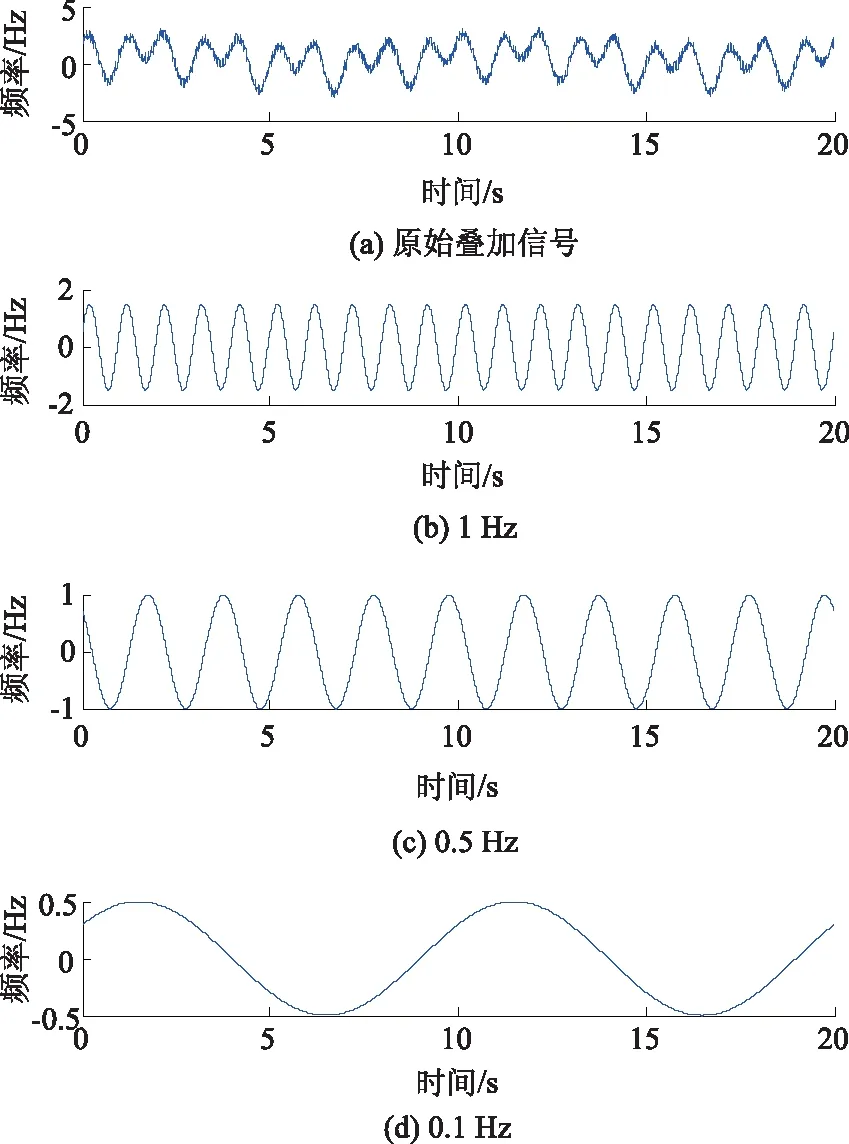
图4 混合信号与叠加信号Fig.4 Mixed signal and superposed signal

4.1 EEMD分解结果

对叠加信号s(t)进行EEMD分解，分解结果见图5，图中第1行为原始信号的时程曲线图，共分解得到10个IMF分量。

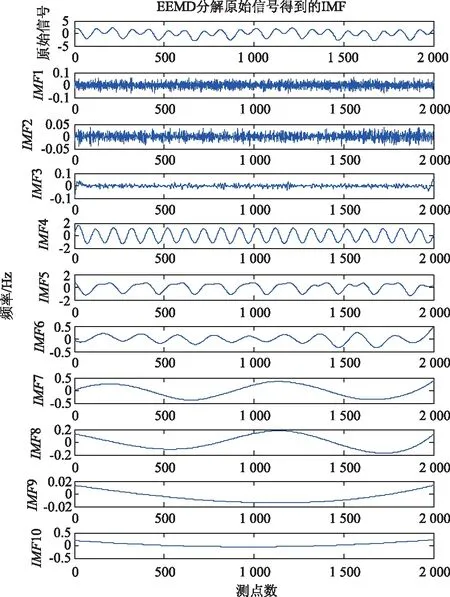
图5 EEMD分解结果Fig.5 Decomposition result by EEMD algorithm

4.2 有效IMF分量

基于3.2节所提算法对上述10个IMF分量进行辨识，得到表1的关联度系数。由表1中数据可知，只有IMF4，IMF5，IMF6对应的关联度数值大于0.3，则将这3列IMF分量定义为有效IMF分量。

将所得有效IMF分量与混合信号中的各组成信号作对比，结果如图6所示。其中有效IMF4分量与1Hz正弦信号的关联度系数为0.89；有效IMF5分量与0.5Hz余弦信号的关联度系数为0.83；有效IMF5分量与0.1Hz正弦信号的关联度系数为0.63。

表1 各IMF分量与叠加信号间的关联度Tab.1 Correlation between IMF component and superposed signal

4.3 改进EEMD分解结果

基于3.3节所提算法，对上述所得IMF4，IMF5，IMF63个有效分量进行Fast-ICA算法处理，并将所得结果与原始信号中的各叠加信号做对比，结果如图7所示。其中有效IMF4分量对应的盲源分离结果与1 Hz正弦信号的关联度系数为0.98；有效IMF5分量对应的盲源分离结果与0.5 Hz余弦信号的关联度系数为0.97；有效IMF5分量对应的盲源分离结果与0.1Hz正弦信号的关联度系数为0.93。

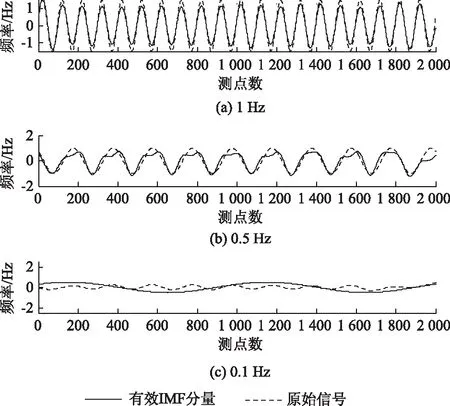
图6 有效IMF分量与各信号的对比Fig.6 Comparison of effectiveness IMF component with signal

图7 有效IMF分量对应盲源分离结果与各信号的对比Fig.7 Comparison of blind source separation result corresponding to effective IMF component with signal

4.4 重构信号

为进一步验证改进EEMD算法所得重构信号更接近真实值，现将两种算法所得重构信号作对比分析，结果如图8所示。由图8可知，本研究所提算法得到的重构信号与原始信号更接近，表明改进EEMD算法能够提高既有EEMD算法的分解效率。

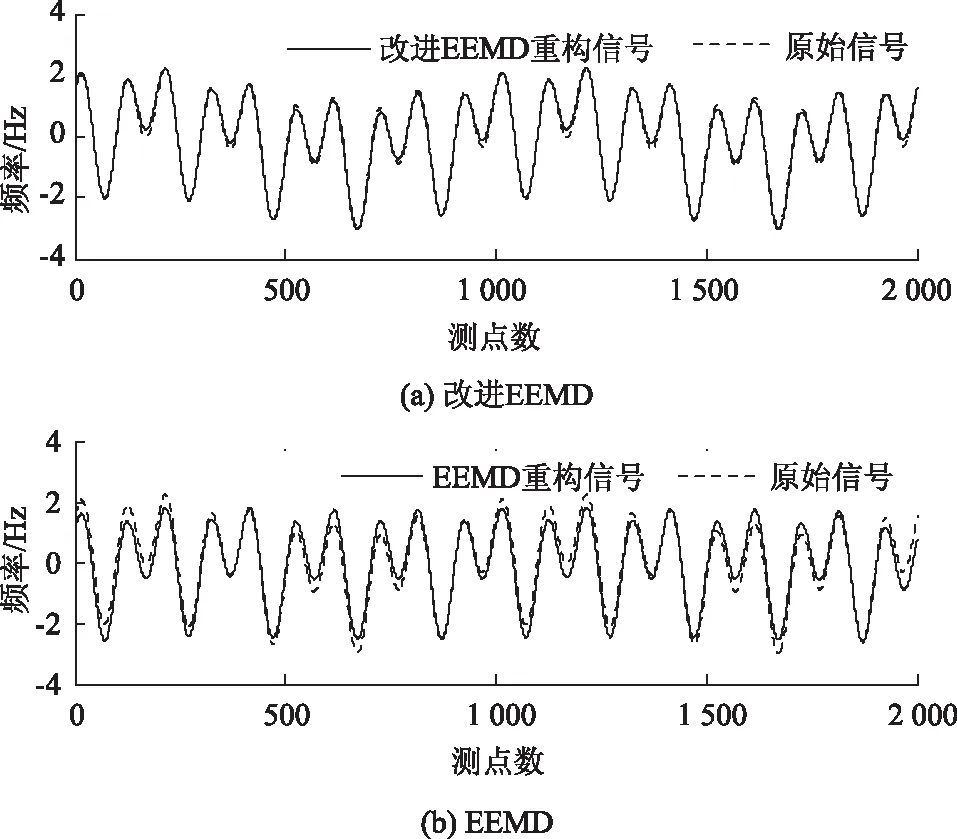
图8 重构信号对比Fig.8 Comparison of reconstructed signals

5 不同噪声水平的信号验证

5.1 各叠加信号

为验证所提算法能够适用于不同噪声水平的信号，在叠加信号s(t)的基础上调整噪声水平，得到新的叠加信号s1(t)和s2(t)：

s1(t)=1.5sin(2πt+π/8)+cos(πt+π/4)+

0.5sin(0.2πt+π/5)+5rand，

s2(t)=1.5sin(2πt+π/8)+cos(πt+π/4)+

0.5sin(0.2πt+π/5)+15rand。

两叠加信号在0～20 s时间段的时程曲线图如图9所示。

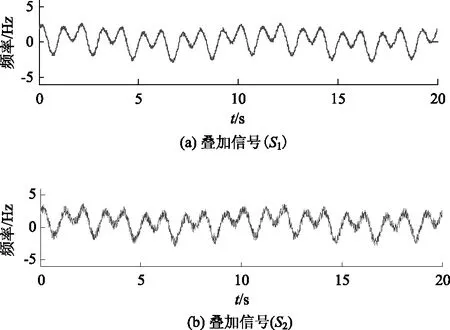
图9 叠加信号Fig.9 Superposed signal

5.2 分解结果

基于第4节的分解流程，分别采用EEMD算法和改进EEMD算法对叠加信号s1(t)和s2(t)进行分解和重构。两种分解算法所得重构信号如图10所示，其中EEMD算法重构所得信号与原始信号间的关联度系数分别为0.83和0.85；改进EEMD算法重构所得信号与原始信号间的关联度系数分别为0.95和0.94。这表明改进EEMD算法适用于不同噪声水平的信号，且分解的效率较既有EEMD算法更高。

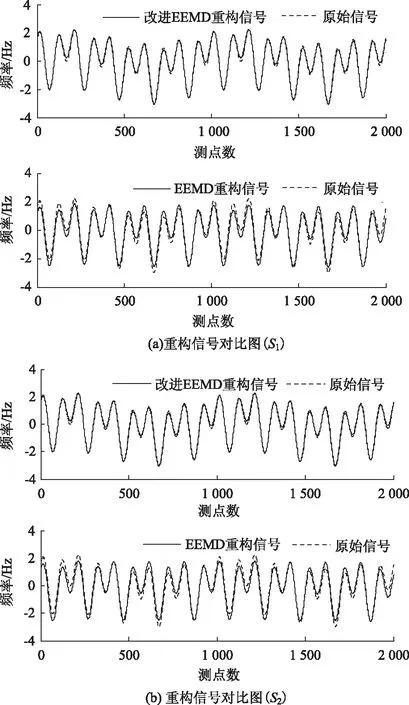
图10 重构信号对比Fig.10 Comparison of reconstructed signals

6 简支梁桥仿真算例

以某简支梁为研究对象，以验证所提算法适用于分解和重构桥梁结构的响应信号。

6.1 简支梁桥

该简支梁的长度为30 m，等分为10段，采用MIDAS软件建立该简支梁模型。其截面为箱型截面。为模拟环境激励，将在节点2～10上分别竖直方向的白噪声激励，如图11所示。

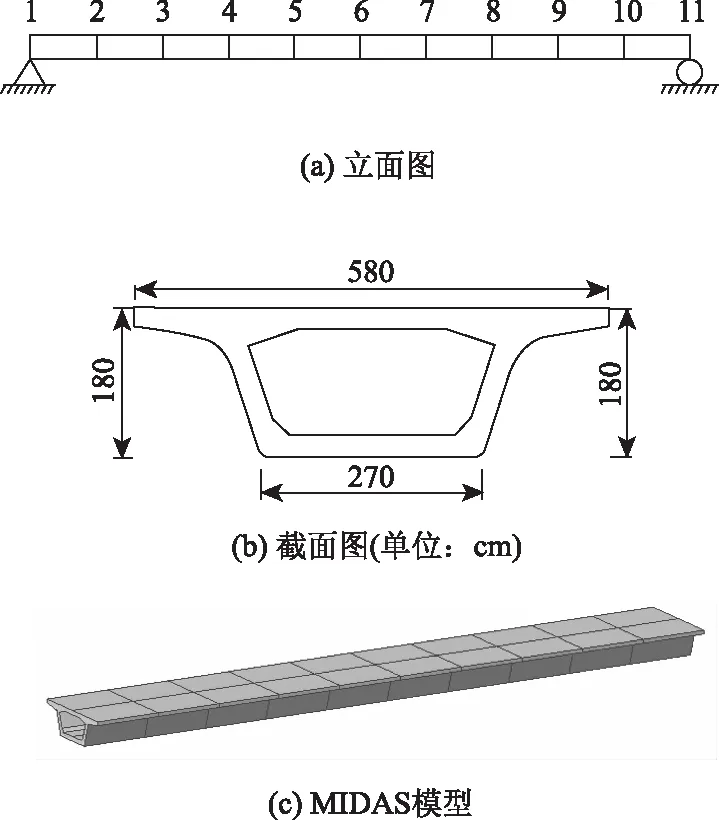
图11 简支梁桥Fig.11 Simply supported girder bridge

6.2 白噪声的添加

白噪声指功率谱密度在整个频域内均匀分布的噪声，添加白噪声激励的步骤如下：

(1)白噪声的生成：基于MATLAB软件中的randn函数命令生成一组均值为0，方差为1的9组随机序列数据；图12为其中一组白噪声激励的时程曲线图。

(2)白噪声的添加：基于MIDAS软件平台，在节点2～10上分别施加一组由Step1所得的随机序列数据，以模拟环境激励；

(3)在MIDAS软件中做时程分析；

(4)提取该简支梁在1 min内各节点的加速度响应信号，因采样频率为100 Hz，即可得到共6 000个测点数据。

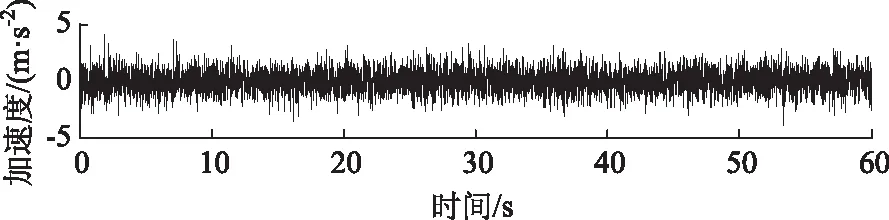
图12 白噪声激励Fig.12 White noise excitation

6.3 各节点的动力响应信号

因篇幅有限，仅给出节点4、节点6及节点8在采样时间段内的加速度响应时程曲线图，见图13所示。

图13 节点加速度响应Fig.13 Acceleration response of node

6.4 模态参数识别结果

分别采用EEMD算法和改进EEMD算法对11个节点的加速度响应信号进行信号的分解和重构，其次再采用随机子空间算法[17-18]识别两种分解算法所得重构信号，得到各自对应的稳定图[19]，见图14。表2给出了两种算法对应的频率值结果与MIDAS时程结果的对比表。

图14 稳定图Fig.14 Stabilization diagrams

根据图14和表2可知：基于改进EEMD算法得到的稳定图中频率轴更为清晰；且基本不存在虚假模态，表明改进EEMD分解算法能够有效地剔除环境激励信号中的无用信息，更为真实地保留桥梁结构自身的结构信息。

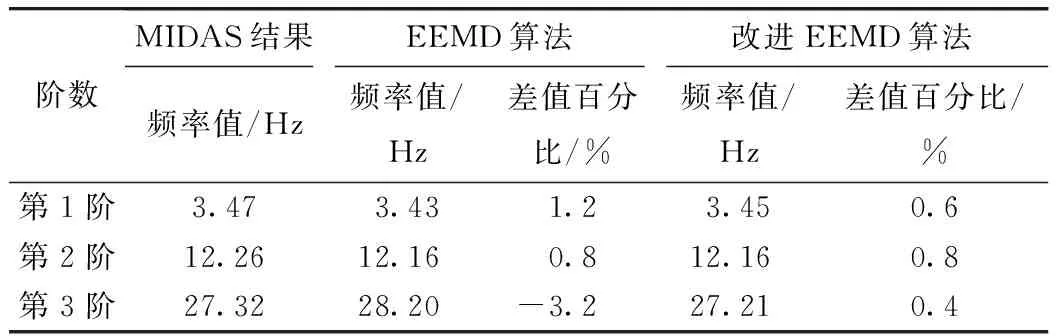
表2 频率结果(单位：Hz)Tab.2 Result of frequency (unit:Hz)

为验证改进EEMD算法能够识别该简支梁结构的模态振型图，得到了其前3阶模态振型图。图15为所得模态振型图与理论振型结果的对比图，其中横坐标为节点编号，纵坐标为经标准化处理后的结构变形结果。可知识别所得前3阶模态振型图均与理论振型图具有很高的相似度。

图15 模态振型识别结果对比Fig.15 Comparison of modal identification results

7 实际桥梁信号验证

以某斜拉桥的实测主梁振动响应信号为研究对象，首先对信号进行分解和重构，其次基于随机子空间算法获得对应的稳定图；最后通过对比所得模态参数结果来辨别两种算法的优劣。

该斜拉桥桥长共628 m，其中主跨为330 m，两边跨均为149 m，桥面净宽18 m。其结构体系为双塔扇形双索面的塔梁分离悬浮体系，桥上总共布置11组加速度传感器，主梁上的圆圈为传感器大体布置位置。传感器的信号采样频率为20 Hz，图16为某传感器采集到的时长为200 s的主梁加速度响应时程曲线图。

图16 加速度响应信号时程曲线Fig.16 Acceleration response signal time-history curve

7.1 真实模态参数结果

对于桥梁结构而言，模态参数结果主要为频率、阻尼比和模态振型。现阶段，由于对阻尼比的认知还不够深入，识别得到的阻尼比结果存在空间和时间的变异性。因此，本研究仅分析该桥梁结构的固有频率和模态振型。

为了获得该斜拉桥的真实固有频率值，已有相关检测单位通过在主梁的主跨跨中采用跳车激振的方式对其产生一定的激励，并基于传感器收集的主梁振动脉冲信号进行分析识别得到了其自振频率。图17为该斜拉桥的前3阶模态振型结果。

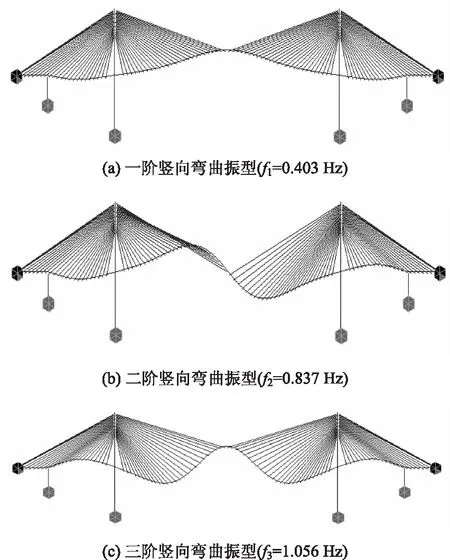
图17 前3阶模态振型(MIDAS)Fig.17 The first 3-order modal shapes(MIDAS)

7.2 稳定图结果分析

采用随机子空间算法识别两种分解算法所得重构信号，得到各自对应的稳定图，结果如图18所示。对比两图可知：基于改进EEMD算法得到的稳定图中频率轴更为清晰；且基本不存在虚假模态，表明改进EEMD分解算法能够有效地剔除环境激励信号中的无用信息，更为真实地保留桥梁结构自身的结构信息。

图18 稳定图结果Fig.18 Result of stability diagrams

7.3 频率值结果分析

为了分析改进EEMD算法所得的稳定图能够获得更为精确的频率值，将两种分解算法所得的前6阶频率值分别与跳车自振结果和MIDAS结果作对比，结果如表3所示。根据表中数据可知:

(1)基于改进EEMD算法所得稳定图中获得的前6阶频率值，其与跳车自振频率值间的差值百分比范围为[-0.9%,1.3%]；与MIDAS频率值结果间的差值百分比范围为[-4.7%,-1.8%]；

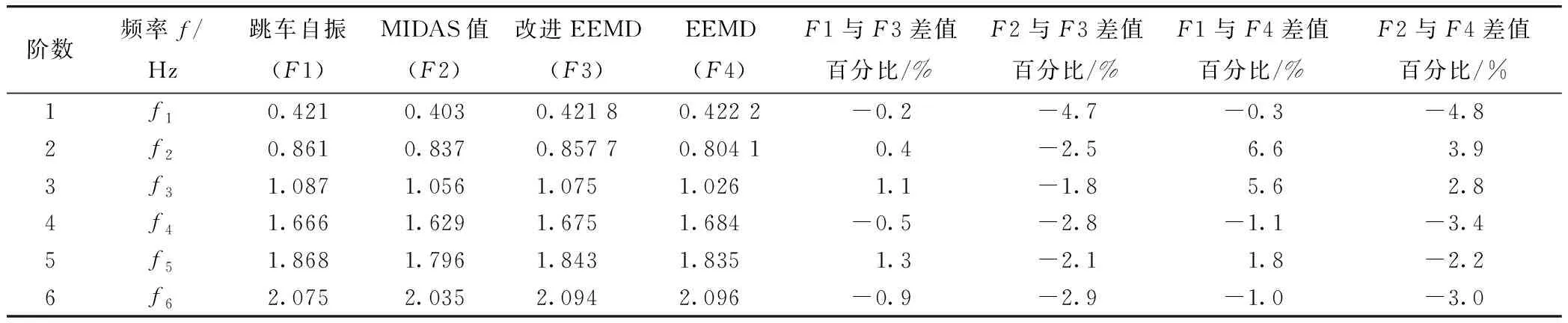
表3 频率值结果对比Tab.3 Comparison of frequencies

(2)基于EEMD算法所得稳定图中获得的前6阶频率值，其与跳车自振频率值间的差值百分比范围为[-1.1%,6.6%]；与MIDAS频率值结果间的差值百分比范围为[-4.8%,3.9%]；

综合上述可知：基于改进EEMD算法和随机子空间算法所得稳定图中频率轴更清晰，且频率值更接近理论值，表明该分解算法较现有的EEMD算法能够更有效地剔除虚假信息，保留实际桥梁结构的真实信息。

7.4 模态振型结果分析

图19为桥梁结构前3阶模态振型图，图中横坐标为传感器布置位置，纵坐标为0-1化结构变形结果。通过对比图19与图17的MIDAS振型图可知：识别所得前3阶模态振型图均与理论振型图具有较高的相似度。

图19 前3阶模态振型Fig.19 The first 3-order modal shapes

8 结论

(1)可以利用“夹角余弦法”来实现有效IMF分量的辨识，且筛选的结果具有可靠性；

(2)将Fast-ICA算法融入到EEMD算法中能够有效避免IMF分量间发生模态混叠现象；

(3)将改进EEMD算法和既有EEMD算法运用于仿真模拟信号中，具有更好的信号分解效率；

(4)将改进EEMD算法和既有EEMD算法运用于实际桥梁工程的信号分解中，并通过对比分析基于随机子空间算法所得的模态参数结果可知，改进算法所得稳定图具有更清晰的稳定轴，频率值和模态振型均具有可靠性。