基于车-桥耦合动力作用的车辆与桥梁力学行为

郝艳广，袁龙文，韩劲龙，梁济川，欧阳彪

(1. 中交二航局建筑科技有限公司, 湖北 武汉 430000; 2. 海工结构新材料及维护加固技术湖北省重点实验室, 湖北 武汉 430040;3. 广东省北江航道开发投资有限公司, 广东 清远 511500)

0 引言

车-桥耦合动力作用包括大量非线性因素，如橡胶轮胎大变形、沥青混合料黏弹性、路面不平度等[1-2]。桥面铺装层分层铺筑，各层材料在环境变化和车-桥耦合动力作用下出现大量病害，如沥青混合料推移、脱落、车辙等,水泥混凝土裂缝、破损等,钢板、钢梁焊接处锈蚀等。这些病害严重影响桥梁工作状态以及服役寿命，相关问题亟待解决[3-4]。

车辆与桥梁相关参数、路面不平度激励以及车桥工作状态对车-桥力学行为有巨大影响[5]。国内外学者针对车-桥耦合动力作用已进行大量研究：张彦玲等[6]研究桥梁在谐波荷载作用下力学行为，结果表明桥梁跨中动挠度受静载影响较大。魏志刚等[7]推导车辆动载作用下桥梁刚度分布函数，根据变形协调方程及荷载平衡条件，得到桥梁动力响应。张玥等[8]基于Midas/FEA软件，建立桥梁模型，研究不同工况下桥梁应力变化规律。李慧乐等[9]建立三维车辆模型与桥梁有限元模型，根据车辆与桥梁接触行为，求解桥梁动态响应。杨永清等[10]建立某公路桥正交异性桥面板有限元模型，研究其在移动荷载下不同桥梁部位应力特征，并基于应力等效原则建立足尺模型验证不同桥梁部位疲劳特性。综上可知，大量车-桥耦合动力研究采用移动荷载、移动质量块或者簧上质量模拟车辆荷载；桥面铺装层材料未能考虑沥青混合料黏弹性；轮胎简化为质量、刚度、阻尼模型，相关研究结果与工程实际存在较大差距。

建立四分之一车辆模型和简支桥模型，其中车辆模型考虑橡胶轮胎，简支桥模型考虑沥青混合料黏弹性。基于轮胎与桥面铺装层接触关系，建立车-桥耦合动力模型，采用中心差分法和有限元理论求解车-桥耦合动力方程以及车辆与桥梁时域响应,将仿真值与测量值进行对比，验证该模型。计算分析桥面铺装层三向应力状态以及不同路面不平度激励下车辆和桥梁力学行为，以期为车辆和桥梁设计提供一定理论依据。

1 四分之一车辆模型

车辆是复杂多自由度系统，一般由车体、悬架、轮胎构成。基于多体动力学理论，在ABAQUS中建立四分之一车辆有限元模型，其中车体假设为均质刚体，轮胎采用橡胶材料模拟。利用连接器将两轮胎分别耦合并采用连接器Hinge属性，模拟车轴；利用连接器将车体与车轴连接并采用连接器Cartesian属性，车辆有限元模型及力学模型如图1所示，相关参数如表1所示。

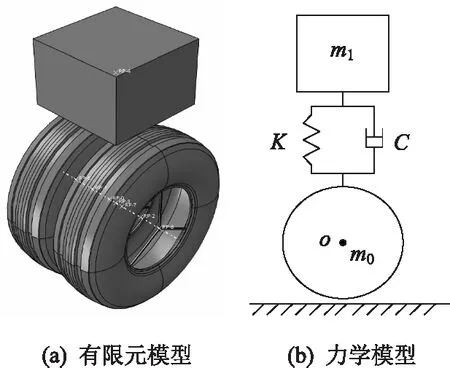
图1 车辆有限元模型与力学模型Fig.1 FE model and mechanical model of vehicle

表1 车辆参数Tab.1 Parameters of vehicle

2 橡胶轮胎模型

相关研究中，轮胎模型均采用如下假设：轮胎由质量、刚度和阻尼构成，根据D′alember原理列出微分方程，并进行求解。实际轮胎是由橡胶基体、帘布层、钢丝帘线等多种材料压制而成。为保证计算精度并提高计算效率，建立橡胶轮胎有限元模型并进行适当简化，保留胎侧与胎面、胎体等橡胶材料以及骨架材料。利用CAD绘制轮胎断面图，导入ABAQUS中生成轮胎有限元模型。轮胎断面图、各部分有限元模型以及相关网格划分如图2所示。

图2 轮胎模型Fig.2 Model of tire

ABAQUS包含Mooney-Rivlin模型、Yeoh模型、Neo-Hookean模型等本构模型，各模型均具有独特性质，针对不同问题，选择适当模型。Yeoh模型适用于描述橡胶材料大变形，本研究采用Yeoh模型。

橡胶具有体积不可压缩非线性力学特点，是三维正交各项异性复合结构物[11]。基于应力-应变关系以及唯象理论建立橡胶材料本构关系，采用体应变能表征其力学特性，其方程如下：

W=W(I1,I2,I3)，

(1)

(2)

(3)

Eij=(λ1λ2)2+(λ2λ3)2+(λ3λ1)2，

(4)

I3=(λ1λ2λ3)2，

(5)

λ=1+γi，

(6)

式中，W为体应变能；I1，I2，I3分别为左Cauchy-green第一、第二、第三张量不变量，当I3=1时，橡胶材料不可压缩；γi为主应变；1，2，3下角标为相互垂直方向，橡胶材料只有单向拉伸，则λ1·λ2·λ3=1；对于橡胶材料，∂W/∂I2远小于∂W/∂I1，一般认为∂W/∂I2在应变能中贡献度很小，可以忽略，则应变能函数简化为[11-13]

(7)

式中Cij为橡胶轮胎材料参数。

橡胶材料参数来自文献[14]，见表2。

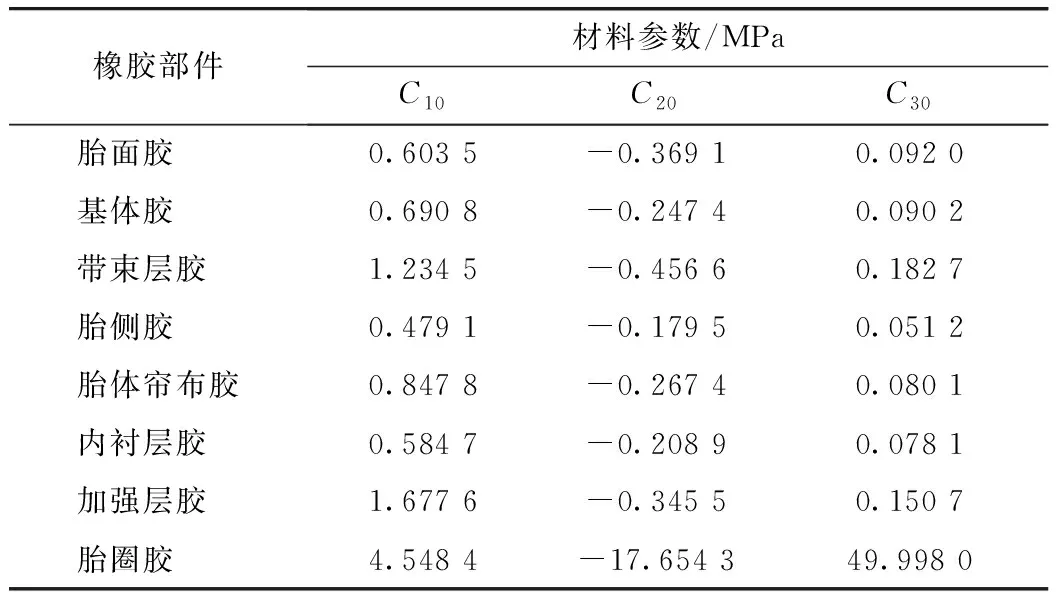
表2 橡胶轮胎参数[14]Tab.2 Parameters of rubber tire[14]

橡胶轮胎主要结构有带束层、胎体帘线、钢丝帘线、钢丝圈等。利用Rebar单元模拟钢丝帘线结构。橡胶材料是轮胎主要成分，采用CGAX4H单元和CGAX3H单元模拟二维橡胶材料，并经空间旋转成三维立体模型，相应单元类型改变为C3D8H单元和C3D6H单元[15]。

3 简支桥模型

简支桥来自江西省某高速公路，全长24 m，采用4块纵向工字钢、21块横向工字钢以及桥面板焊接而成。纵梁高1.6 m，间距3 m，纵梁梁顶与桥面板底面焊接；横梁高0.4 m，间距4 m，横梁梁端与纵梁侧面焊接。纵梁、横梁、桥面板均采用Q345钢，桥面铺装层相关材料参数如表3、表4所示。

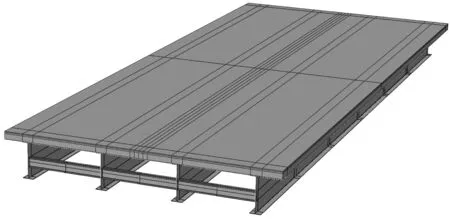
图3 简支桥模型Fig.3 Model of simply supported bridge

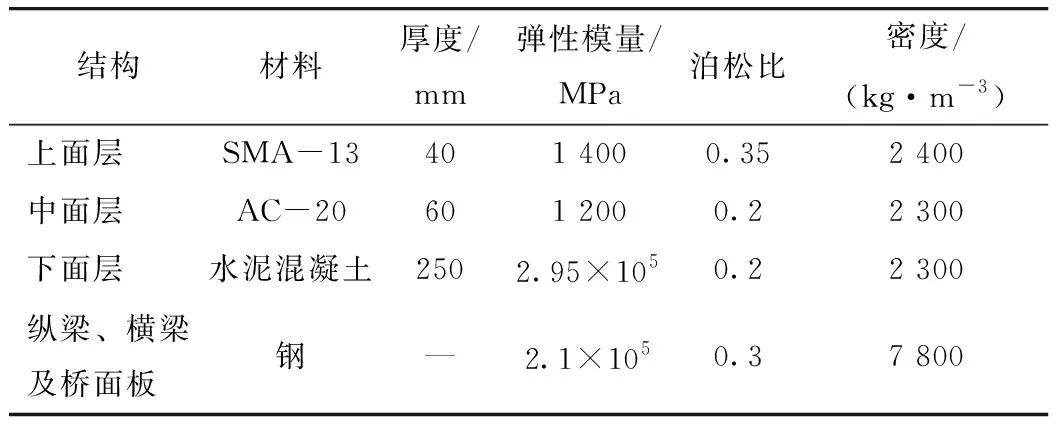
表3 桥面铺装层材料参数Tab.3 Material parameters of deck pavement

水泥混凝土采用线弹性本构模型；沥青混合料具有黏弹性，采用广义Maxwell模型模拟，广义Maxwell模型如图4所示。

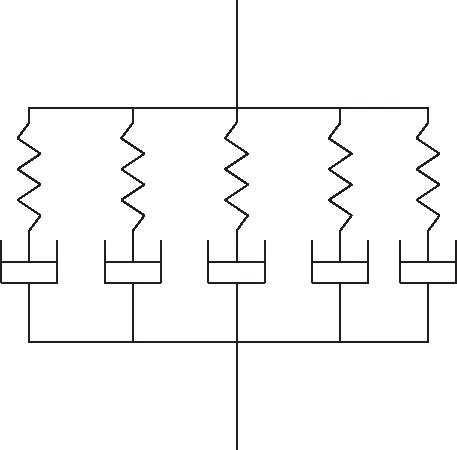
图4 广义Maxwell模型Fig.4 Generalized Maxwell model

对广义Maxwell模型施加一定应变，每一个Maxwell元件均有同样应变，则：

σi=ε0Eiexp(-t/τi)，

(8)

总应力为:

(9)

则松弛模量函数为:

(10)

当t=0时

(11)

式中，E0为初始松弛模量；Ee为松弛时间t无穷时刻平衡值；σ(t)为应力；ε0为初应变。

广义Maxwell高分子聚合物经典遗传积分形式可以写成:

(12)

式中，σ0(s)为弹性响应部分；g(t)为衰减函数，采用Prony级数表示：

(13)

沥青混合料黏弹性参数来自文献[16]。

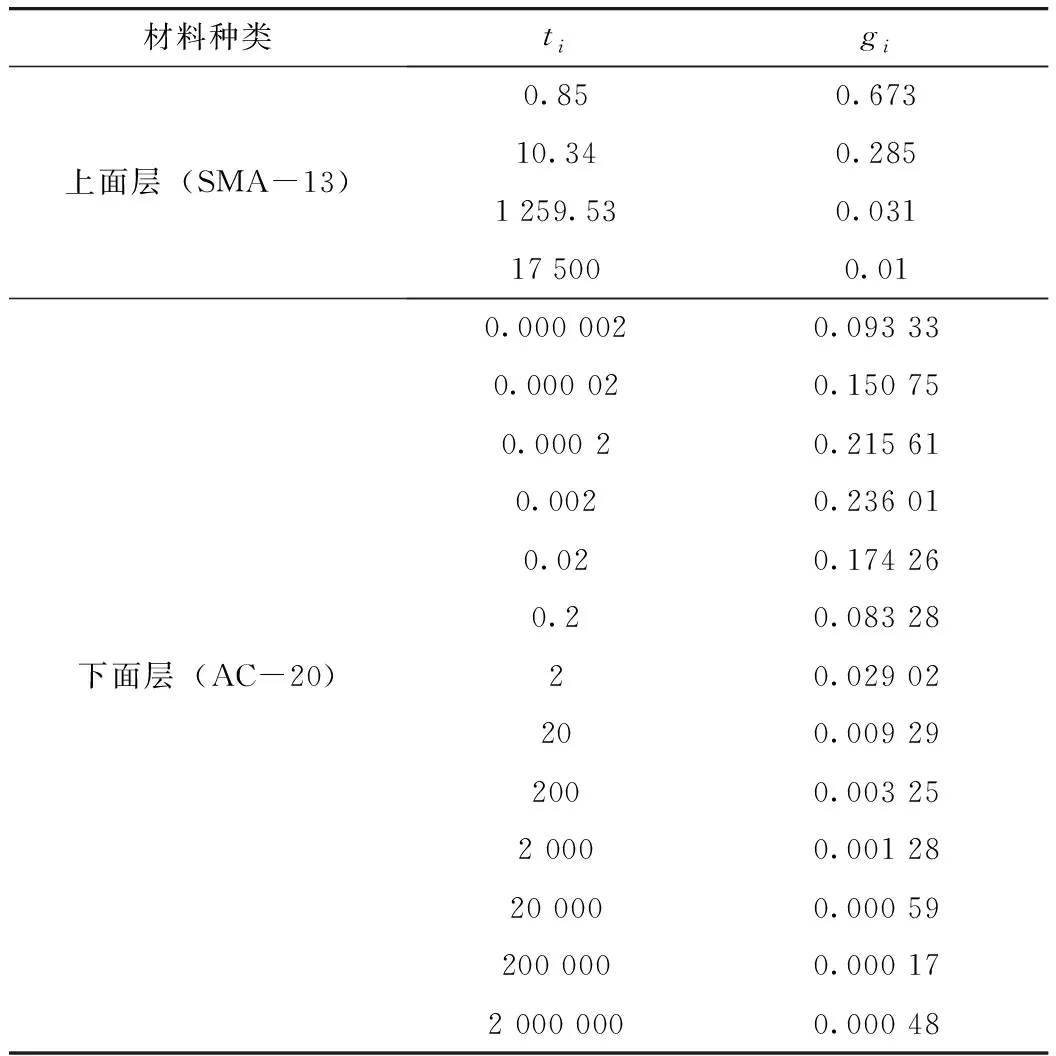
表4 黏弹性参数[16]Tab.4 Parameters of viscoelasticity[16]

4 车-桥耦合动力模型

4.1 路面不平度

路面不平度是车-桥耦合振动主要原因，由《机械振动道路路面谱测量数据报告》(GB/T 7031—2005/ISO 8608: 1995)可得路面功率谱表达式为

Gq(n)=Gq(n0)|n/n0|-ω,

(14)

式中，n0=0.1 m-1，为空间参考频率；n为任意有效空间频率；Gq(n0)为参考空间频率对应的功率谱密度，B级路面取64×10-6m2/m-1；ω为频率指数，用于确定路面不平度的频率结构，通常取2。B级路面不平度如图5所示。

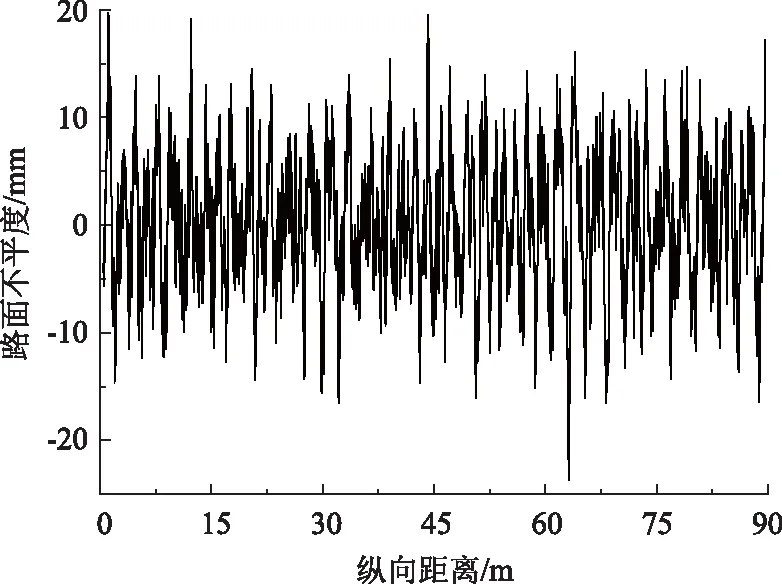
图5 B级路面不平度Fig.5 Class B pavement roughness

4.2 接触关系

轮胎与桥面接触关系可分为法向接触行为和切向接触行为。法向接触行为采用“硬接触”表示，并通过罚函数计算法向力:

(15)

式中，kn为法向接触刚度；C为间隙值。

切向接触行为采用库伦摩擦力表示，摩擦力数值取决于轮胎与路面接触状态

(16)

式中，kt为切向刚度；ne为接触节点相对变形；μ为摩擦系数。

4.3 边界条件

约束桥梁两端相关自由度，模拟简支桥边界条件。为保证橡胶轮胎自由滚动，对连接器施加沿z方向平动速度。桥面设置摩擦系数μ，轮胎与桥面之间摩擦力推动轮胎滚动，如图6所示。

图6 轮胎旋转示意图Fig.6 Schematic diagram of tire rotation

4.4 求解车-桥耦合动力方程

车-桥耦合动力模型分为车辆模型和桥梁模型，基于有限元理论将车辆、桥梁模型分别离散，如图7所示。

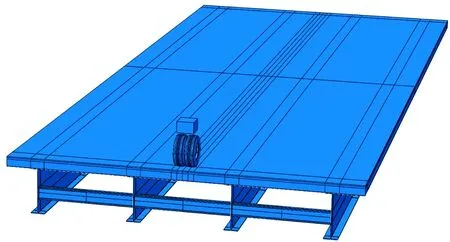
图7 车-桥耦合动力模型Fig.7 Vehicle-bride coupling dynamic model

通过轮胎-桥面接触关系实现两模型之间力学关系转换。路面不平度作为外部激励，形成车-桥耦合，其耦合效应随路面平整度降低而加剧[17-20]。接触理论将轮胎与桥面接触关系转换成时域上连续接触关系，则车-桥耦合动力方程为:

(17)

式中，Y″，Y′，Y分别为加速度、速度、位移向量；M，C，K分别为质量、阻尼、刚度矩阵；下角标v，r分别表示车辆和桥梁；Rv，Rr分别为车辆与桥梁恢复力；Pvr，Prv分别为车辆与桥梁之间作用力。

所建模型考虑轮胎与桥面之间摩擦以及多种非线性材料，导致耦合动力方程中阻尼矩阵和刚度矩阵为非对称矩阵。针对这一问题，拟采用中心差分法求解。中心差分法每一时间步积分步长可由下式确定:

(18)

式中，Tn为有限元模型最小固有频率。加速度和速度分别为:

(19)

(20)

将式(19)和式(20)代入式(17)，可求得每个时间步位移。由有限元理论可知，位移与应变存在如下关系

εe=BYe，

(21)

σe=Dεe，

(22)

σe=DBYe，

(23)

式中，εe为单元应变；σe为单元应力；Y为单元节点位移；B为位移-应变关系矩阵；D为弹性矩阵。

综上所述，建立车-桥耦合动力方程，并基于中心差分法和有限元理论求解，可得车-桥耦合动力作用下时域响应，如位移、应力等。

5 力学行为分析

5.1 模型验证

为验证所建模型可行性，将上面层跨中竖向应力仿真值与测量值进行比较。待中面层沥青混合料铺设完成后，在桥梁跨中截面布设土压力盒以及连接导线，然后铺设上面层沥青混合料。相关施工工序完成后，进行车-桥耦合测量试验，测量车辆动载作用下桥面铺装层应力变化状态。土压力盒布设如图8所示，对比结果如图9所示，速度取30 m/s。

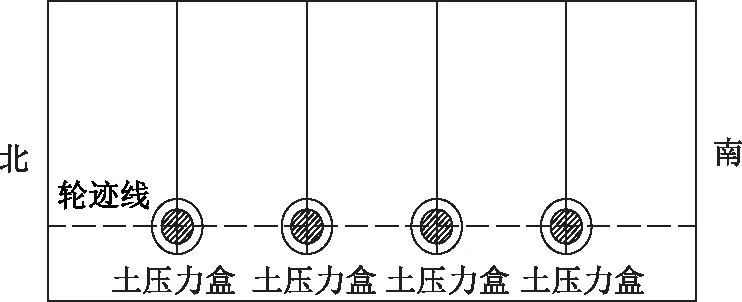
图8 土压力盒布设示意图Fig.8 Schematic diagram of layout of earth pressure boxes

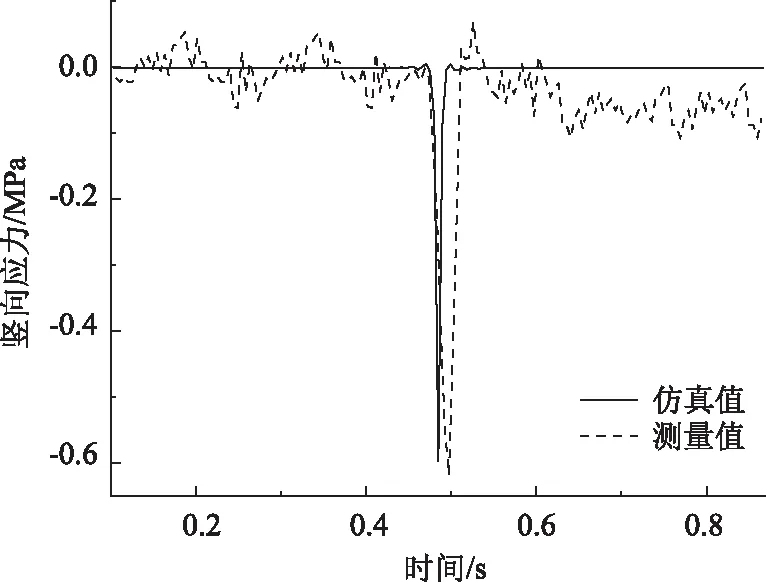
图9 上面层竖向应力Fig.9 Vertical stress of upper surface layer

由图9可知，车辆动载作用下，上面层跨中竖向应力仿真值为0.608 MPa，测量值为0.630 MPa，比仿真值大3.618%，表明基于相关理论构建车-桥耦合动力模型具有一定可行性，相关计算方法恰当。

5.2 铺装层三向应力

以桥面铺装层跨中为观测点，提取该点三向应力时程曲线，分析车辆动载作用下桥面铺装层动力响应。

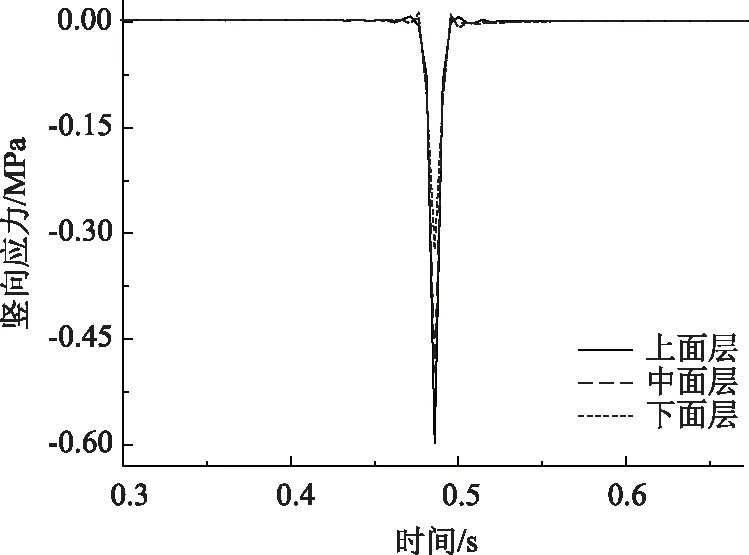
图10 桥面铺装层竖向应力Fig.10 Vertical stress of bridge deck pavement

由图10可知，车辆动载作用下，桥面铺装层竖向应力以受压为主，上、中、下面层最大竖向压应力分别为0.608，0.507，0.330 MPa，竖向压应力随桥面铺装层深度增加逐渐降低。

由图11可知，车辆动载作用下，桥面铺装层横向应力以受压为主，并呈现出一定的振动形态。上、中、下面层最大横向压应力分别为0.283，0.245，0.227 MPa，横向压应力随桥面铺装层深度增加逐渐减小。

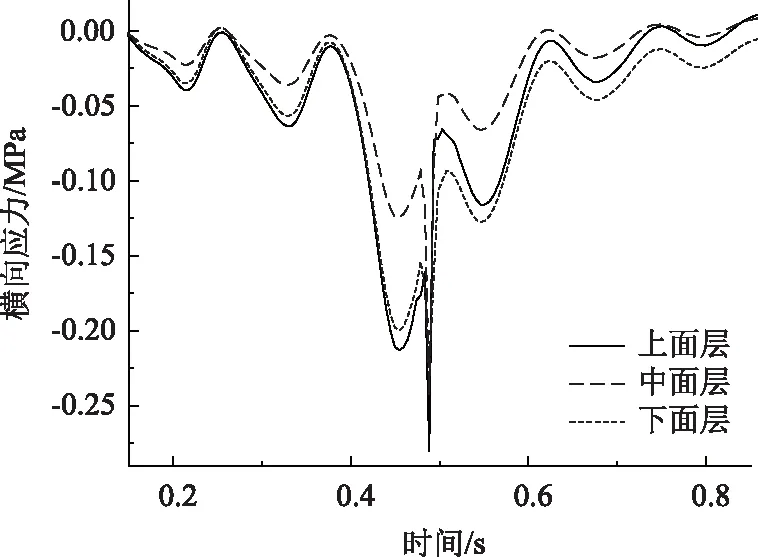
图11 桥面铺装层横向应力Fig.11 Transverse stress of bridge deck pavement

由图12可知，车辆动载作用下，桥面铺装层纵向应力以受压为主，上、中、下面层最大纵向压应力分别为0.338，0.277，0.245 MPa，纵向压应力随桥面铺装层深度增加逐渐减小。

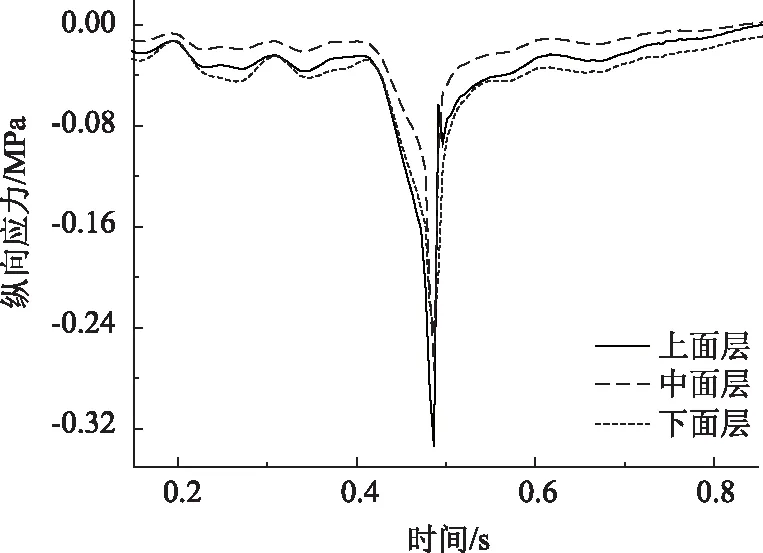
图12 桥面铺装层纵向应力Fig.12 Longitudinal stress of bridge deck pavement

5.3 路面不平度对力学行为影响

本研究构建B级路面不平度，探究路面不平度激励对桥面铺装层、钢桥部件以及车辆动态响应影响规律。

5.3.1上面层跨中

由图13可知，添加B级路面不平度，上面层跨中最大竖向压应力为1.327 MPa，比未添加不平度增大118.257%。

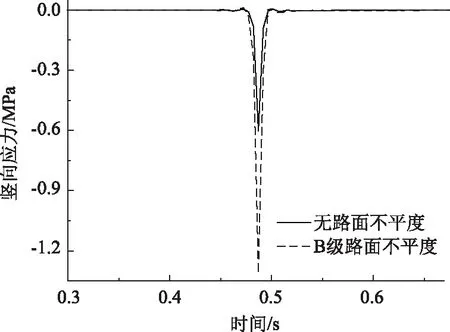
图13 不同路面等级上面层竖向应力Fig.13 Vertical stress of upper surface layer in different road grades

由图14可知，添加B级路面不平度，上面层跨中最大横向压应力为0.652 MPa，比未添加不平度增大130.389%，且横向应力时程曲线振动形态加剧。

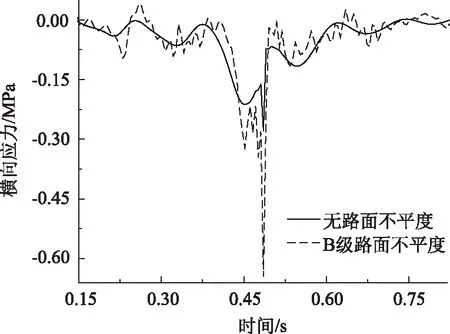
图14 不同路面等级上面层横向应力Fig.14 Transverse stress of upper surface layer in different road grades

由图15可知，添加B级路面不平度，上面层跨中最大纵向压应力为0.706 MPa，比未添加不平度增大108.876%，且纵向应力时程曲线呈现出波动状态。

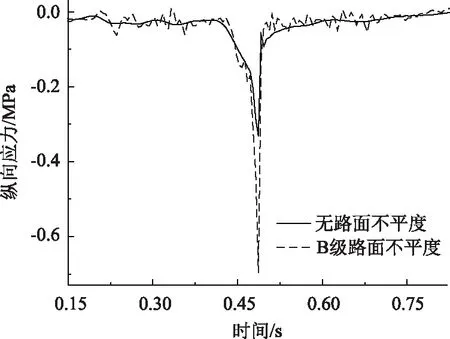
图15 不同路面等级上面层纵向应力Fig.15 Longitudinal stress of upper surface layer in different road grades

5.3.2钢板顶面

由图16可知，未添加路面不平度，钢板顶面跨中最大竖向压应力为0.012 MPa；添加B级路面不平度为0.027 MPa，比未添加不平度增大125%。

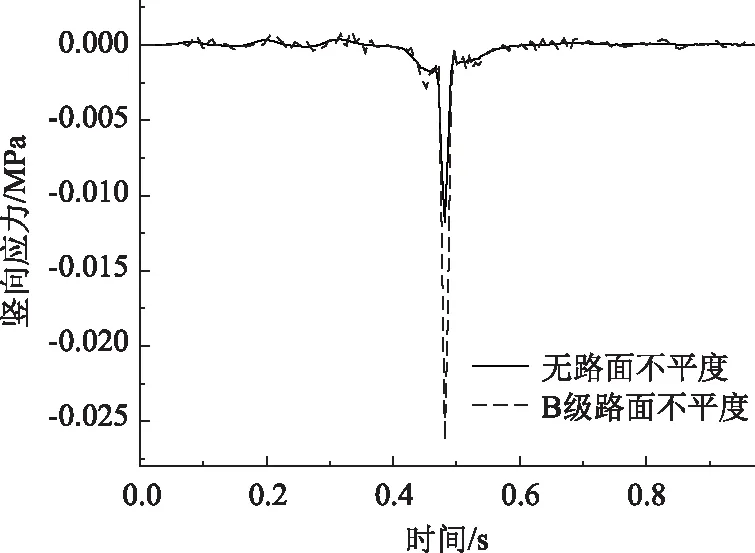
图16 不同路面等级钢板顶面竖向应力Fig.16 Vertical stress of top surface of steel plate in different road grades

由图17可知，未添加不平度，钢板顶面跨中最大横向拉应力为1.290 MPa；添加B级路面不平度为2.210 MPa，比未添加不平度增大71.318%，且横向应力时程曲线振动加剧。

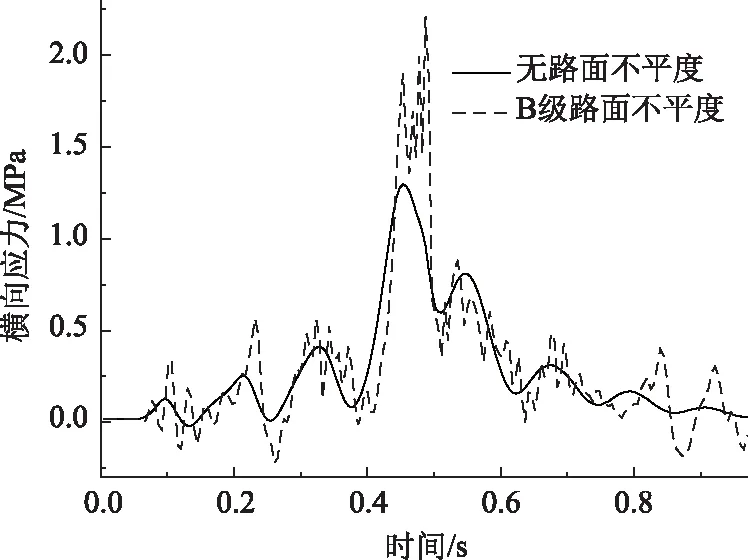
图17 不同路面等级钢板顶面横向应力Fig.17 Transverse stress of top surface of steel plate in different road grades

由图18可知，未添加不平度；钢板顶面跨中最大纵向拉应力为0.793 MPa；添加B级路面不平度为2.030 MPa，比未添加不平度增大155.990%。

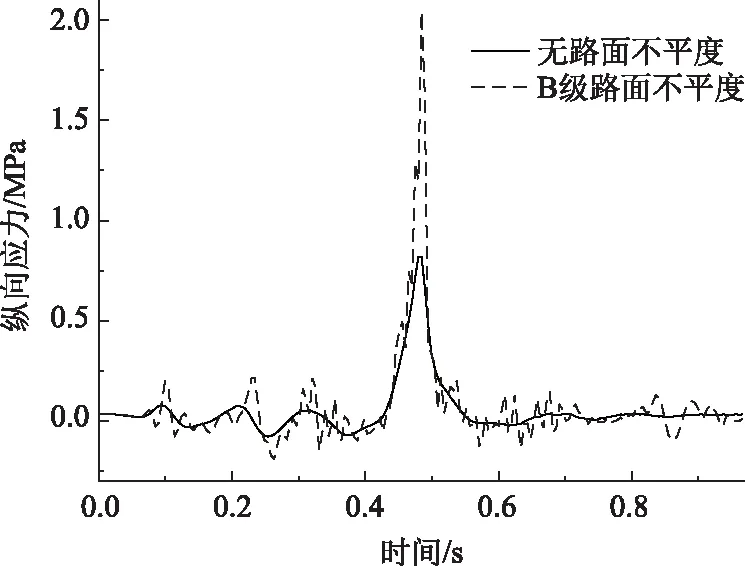
图18 不同路面等级钢板顶面纵向应力Fig.18 Longitudinal stress of top surface of steel plate in different road grades

5.3.3车辆悬架

由图19和图20可知，添加B级路面不平度，车辆悬架弹力与阻尼力均增大，车辆振动明显，车-桥耦合动力效应增强。未添加不平度，最小和最大车辆悬架弹力分别为36.178，59.322 kN，变化幅度为63.973%；添加B级路面不平度，最小和最大悬架弹力分别为33.738，60.859 kN，变化幅度为80.387%。

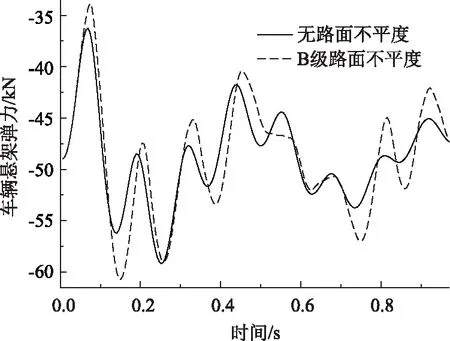
图19 不同路面等级车辆悬架弹力Fig.19 Elastic force of vehicle suspension in different road grades

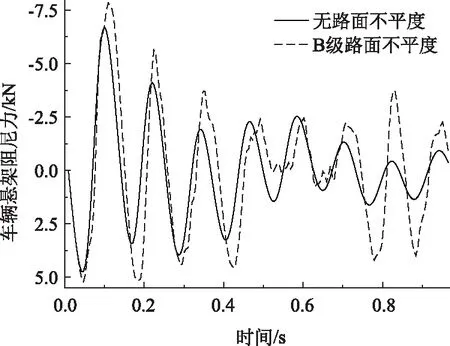
图20 不同路面等级悬架阻尼力Fig.20 Damping force of vehicle suspension in different road grades

5.3.4纵梁跨中

由图21可知，未添加不平度，纵梁跨中最大竖向拉应力为0.105 MPa，最大竖向压应力为0.282 MPa；添加B级路面不平度，纵梁跨中最大竖向拉应力为0.209 MPa，最大竖向压应力为0.449 MPa，分别比未添加不平度增大99.048%、59.220%。

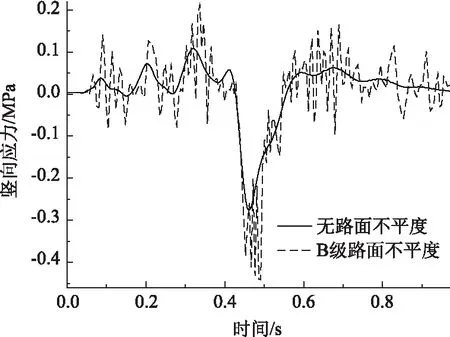
图21 不同路面等级纵梁竖向应力Fig.21 Vertical stress of vertical beam in different road grades

由图22可知，未添加不平度，纵梁跨中最大横向拉应力为0.167 MPa，最大横向压应力为0.193 MPa；添加B级路面不平度，纵梁跨中最大横向拉应力为0.365 MPa，最大横向压应力为0.418 MPa，分别比未添加不平度增大118.563%,116.580%。

图22 不同路面等级纵梁横向应力Fig.22 Transverse stress of vertical beam in different road grades

由图23可知，未添加不平度，纵梁跨中最大纵向拉应力为0.046 MPa，最大纵向压应力为0.159 MPa；添加B级路面不平度，纵梁跨中最大纵向拉应力为0.309 MPa，最大纵向压应力为0.348 MPa，分别比未添加不平度增大245.652%,118.868%。

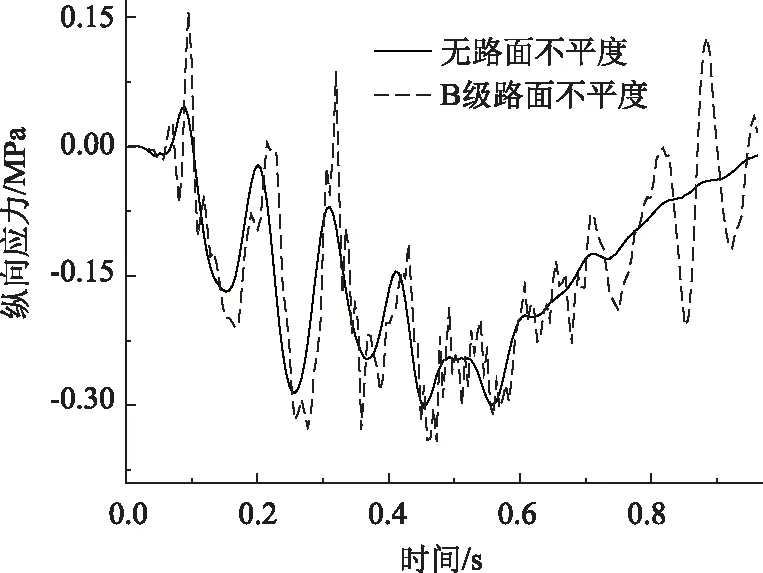
图23 不同路面等级纵梁纵向应力Fig.23 Longitudinal stress of vertical beam in different road grades

由以上分析可知，车辆动载作用下，纵梁跨中三向应力均以受压为主。受不平度以及车辆振动影响，当车辆接近或远离观测点时，纵梁跨中三向应力均表现出一定拉应力。桥面铺装层为B级路面不平度时，三向应力极值均增大，且应力时程曲线呈现出一定波动状态，应力状态复杂。

6 结论

本研究建立两自由度四分之一车辆模型和简支桥模型，将桥面铺装层上面层跨中竖向应力仿真值与测量值对比，验证该模型,进一步分析桥面铺装层三向应力状态以及不同路面等级下各项力学行为变化规律。结果表明：

(1)车辆动载作用下，上面层跨中竖向应力测量值比仿真值大3.618%，表明所建车-路耦合动力模型具有一定可行性。

(2)车辆动载作用下，三向压应力随桥面铺装层深度增加逐渐降低。

(3)桥面铺装层为B级路面时，车-桥耦合效应增强，车辆与桥梁各项响应均增大。在桥梁运营期间应严格控制路面不平度，防止车辆以及桥梁耦合振动效应加剧。

(4) 因现场试验条件有限，无法保证改变车辆重量后相关测量数据的准确性，故只进行了车辆满载工况下，相关动力响应的测试与分析，并建立该工况有限元模型，验证其正确性。在后续研究中，将考虑多种工况，为理论分析提供更全面的参考。