“高观点”下柯西不等式的应用探究*

湖南省娄底市湖南人文科技学院(417000) 莫元健 龙承星

柯西不等式作为高中数学新课程中的新增内容,其形式简洁,应用广泛,极具解题魅力.近年来,无论是高考试卷还是数学不同学科的题目中都越来越多地出现了与柯西不等式相关的题目.用高等数学中柯西不等式的思想渗透到中学数学中,对解决中学数学中某些不等式的证明或灵活并巧妙地在不同数学学科中应用柯西不等式,将得到出奇制胜、事半功倍的效果.

1 柯西不等式

1.1 柯西不等式的定义

在中学中我们熟知柯西不等式的左边是平方和的乘积,右边是乘积和的平方.但在高等数学中,柯西不等式这一定义表达形式将得到延伸,它不仅形式多变,其应用范围也从中学中二维形式、三维形式演变成高等数学的向量、积分等形式.

柯西不等式不同形式的推广,是求解常见不等式问题的过渡桥梁,柯西不等式在中学数学和高等数学中都有着明确定义,如表1 所示:

1.2 柯西不等式的应用范围

柯西不等式被广泛应用于初等数学、高等代数、微积分、线性代数、概率论等领域,其在不同领域有不同形式[2].柯西不等式有很多种证明方法,不同方法优劣不一,我们在认真了解不同方法证明的条件和特点的同时可推出柯西不等式的各种推广公式.

表1 柯西不等式的形式比较

形式上: 灵活巧妙地运用柯西不等式能解决不等式证明、三角形求解、最值求解、方程求解等问题.更精彩的是可以利用柯西不等式得出的推广公式以简捷和严谨的方式来解决其它公式不容易解决的实质性问题.

结构上: 呈对称性,柯西不等式在代数学、几何学中都得到广泛的应用.数学工作者对有关柯西不等式的钻研与适用的范围不断拓展,方法层出不穷,使柯西不等式得到了丰富与发展[3].

1.3 几何图形视角中的柯西不等式

2002年北京国际数学家大会的会标“赵爽弦图”引入了几何图形[4],该几何图形中隐含不等关系:a2+b2≥2ab,以图1 为例,我们设由拼接所构成的平行四边形它的一个内角为θ,则

图1 赵爽弦图

从另一方面可得到:

由①②可得:

两边平方即可得到

当且仅当sinθ=1,即θ=90°时取到等号,此时两个直角三角形相似,可得到等号成立的条件是ad=bc.

2 柯西不等式在中学数学教学中的应用

柯西不等式为不等式选讲的第三讲内容,在中学教材中承前启后,应用柯西不等式能处理中学中一些典型的数学问题.特别是在不等式的证明中,如果适时巧妙地引入柯西不等式,不仅简化解题过程,而且对解题有很大的帮助.

2.1 柯西不等式在不等式证明中的应用

利用柯西不等式证明不等式的关键是恰当构造变形,化为符合它的形式,当一个式子与柯西不等式的左边或者右边具有一般形式时,就可以使用柯西不等式进行证明[5].

例1(2017-高考江苏卷) 已知a,b,c,d为实数,且a2+b2=4,c2+d2=16,证明ac+bd≤8.

证由柯西不等式可得:(a2+b2)(c2+d2)≥(ac+bd)2(a,b,c,d ∈R), 因为(a2+b2)= 4,(c2+d2)=16,所以(ac+bd)2≤64,所以ac+bd≤8.

小结很多重要不等式都可由柯西不等式证明,而且利用柯西不等式很容易将一些简单不等式推广.在应用柯西不等式时,要注意右边为常数且应留意等号成立得条件.

2.2 柯西不等式在数列求解问题中的应用

在高考中柯西不等式和数列构造法结合常常贯穿于求解数列题目中,旨在展现柯西不等式在解决数列问题中的广泛运用,如下简要分析的等比数列题目运用等比数列构造法和柯西不等式背景下解题的典型例子.

例2(2008-陕西省高考卷) 已知数列{an}的首项为:(n=1,2,...),证明a1+a2+...+

证先求出通项公式an, 再借助柯西不等式进行放缩.由已知得所以数列是等比数列, 公比为首项为,于是故记

由柯西不等式得a1+a2+...+an=≥

小结柯西不等式和数列构造法联合求解是一种打破数学一贯的解题思路,通过观察、联结、构造出满足解题条件的数学对象,能将复杂问题简单化的一种解题方法.掌握构造法对提升学生思维的创新性、灵活性都有十分重要的意义[6].

2.3 柯西不等式在三角问题中的应用

在解答三角问题时,很多同学往往只会就题论题,快速的写出答案了事,忽略了数学问题应该善于发挥,扩展思路,一题多证.就题论题会使学生头脑中的知识散乱,形不成系统,致使学生的空间思维缩小.柯西不等式在解决三角问题的方法中也频频涉及.

例3设P是∆ABC内的一点,x,y,z是P到三边a,b,c的距离,R是∆ABC外接圆的半径,证明

证由柯西不等式得:

记S为∆ABC的面积,则ax+by+cz=2S=

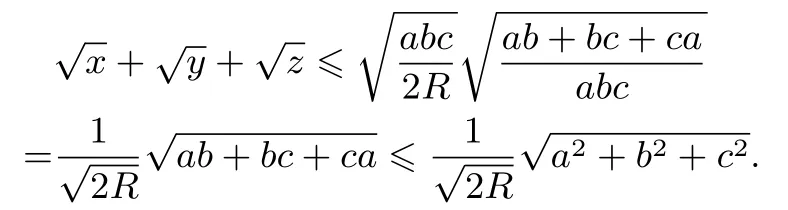
故不等式成立.

小结三角问题通常包含三角不等式,三角方程,三角极值等,在一些三角问题中,为了应用柯西不等式我们创造必要条件,从而引进一些待定参数,其值得确定也由题设或者由等号成立的充要条件共同确定,由此三角极值问题我们可以反复应用柯西不等式进行解决[7].

2.4 柯西不等式在方程问题解决中的应用

柯西不等式也常常应用在解决方程问题中,使得计算更为简便快捷.

例4(2017年全国高中数学联赛陕西省预赛) 若实数a,b,c满足a+2b+3c= 6,a2+4b2+9c2= 12,则abc的值是:____.

解由题设和柯西不等式得36 = (a+2b+3c)2≤(12+12+12)(a2+4b2+9c2)= 36, 当且仅当a= 2b=3c=即a=2,b=1,c=时等号成立,所以abc=

例5解方程组

解原方程组可化为运用柯西不等式得两式相乘, 得(x2+y2+z2)·(x2+w2)≥486,当且仅当x=y=z=w时取等号.故原方程的解为x=y=z=w=3.

小结巧用柯西不等式求解无理方程,是先把方程(含有无理式)应用柯西不等式化为不等式,而后联合原方程把不等式又化成等式,在判定为等式之后再利用柯西不等式取等号的共性, 求得与原方程同解且比原方程简单的无理方程,进而得到简单的整式方程,从而求得原方程的解[8].

3 柯西不等式在高等数学中的应用

教师教学与学生学习的目的是通过学习理论知识转化成自己的思想,在实践中能够学以致用,从而达到锻炼自己的思维能力.

我们在实践教学中通常通过利用柯西不等式求参数的取值范围、证明等式的成立、解决极值问题来推广柯西不等式在高等数学中的具体应用[9].学生通过不同题型的训练自己具备分析的能力.

3.1 柯西不等式在线性代数中的应用

一般线性代数或高等代数教材中往往涉及柯西不等式的内容.

定理1设α=则(α,β)2≤(α,α).(β,β).

证若α为零向量, 结论显然成立; 设α为非零向 量,对任意的t ∈R,有(tα+β,tα+β) ≥ 0, 即(α,β)t2+2(α,β)t+(β,β)≥0,因为(α,α)>0,所以∆=4(α,β)2−4(α,α).(β,β)≤0,故(α,β)2≤(α,α).(β,β).

小结一般线性代数或高等代数教材通常是利用向量α,β的线性 组 合α+tβ来构造内积, 而由内积(tα+β,tα+β)的非负性,证得柯西不等式.

3.2 柯西不等式在空间解析几何中的应用

柯西不等式不仅形式优美,而且应用非常广泛,不但可以解决代数中重要不等式问题,而且还能解决解析几何中的有关问题,本文例析空间解析几何中的柯西不等式问题的应用如下.

定理2[10]设a,b为两个向量,则|a·b|≤|a|·|b|.

证设a,b的夹角为θ, 则a·b=|a|·|b|cosθ, 因为|cosθ|≤1,所以|a·b|≤|a|·|b|.

例6求的最大值与最小值.

解令向量a=(2 sinθ,b=(1,sinϕ,cosϕ),由柯西不等式

小结柯西不等式在结构上对称,无论是在代数学中,还是在几何学中都得到广泛的应用,柯西不等式能有效解决解析几何中问题.

3.3 柯西不等式在定积分中的应用

柯西不等式有各种各样的类型,在不同的数学领域中都有着极其广泛的应用.它在定积分中也广泛应用着.

定理3设f(x),g(x)在[a,b]上连续,则有

证若f(x)≡0 时,结论显然成立;设f(x)不恒为零,则对任意的t ∈R,由[tf(x)+g(x)]2≥0得f2(x)t2+f(x)g(x)t+g2(x)≥0,两边在[a,b]上关于x积分得

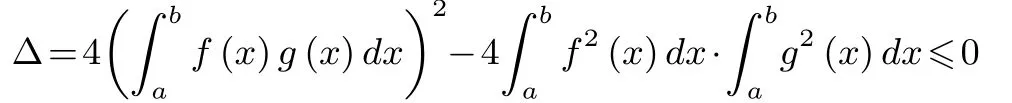
例7设f(x),g(x)在区间[a,b]上均连续,证明:

证(1)对任意实数λ,有即左边是一个关于λ的二次多项式,它非负条件是其判别式非正,即从而本题得证.

小结柯西不等式不同的形式和内容对应于不同的数学领域,其能启发人得到灵活多样的证明思维,但其本质是不变的,所以这些都充分体现了数学各领域间的内通行、渗透性和统一性.在定积分中亦如此[11].

4 高等数学中柯西不等式的思想和方法对中学数学解题的指导

柯西不等式是高等数学中重要的不等式,并且在初等数学中也有着广泛的应用,对初等数学的解题有很大帮助.

例8设x,y,z ∈R,2x −y −2z=6,试求x2+y2+z2的最小值.

解考虑以下两组向量u= (2,−1,−2),v= (x,y,z),根据柯西不等式(u·v)2≤|u|2·|v|2,有

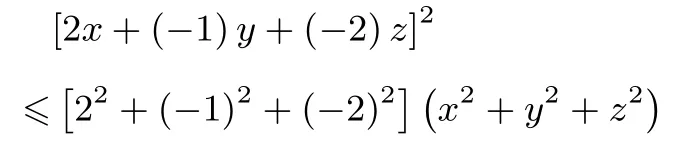
即(2x −y −2z)2≤9(x2+y2+z2),将2x−y −2z=6 代入其中,得36 ≤9(x2+y2+z2),而有x2+y2+z2≥4,所以x2+y2+z2最小值为4.

例9证明n个实数平方的平均数不小于n个数的算术平均数的平方, 即若a1,a2,...,an ∈R, 则有

证有柯西不等式变形得

小结这是我们初等数学中, 常用得不等式, 而此题将初等数学中得“算平均”,“几何平均”问题扩展到了“二次幂平均问题”, 即≤这不仅拓宽了中学生得知识面,而且为许多不等式开辟了一条新路.

5 结语

柯西不等式在整个数学体系中占有非常重要的地位.实践教学中要引导学生深入了解柯西不等式的定义,理解柯西不等式的证明.学生在学习过程中要注重锻炼自己的逻辑思维能力与发散思维能力,并能够运用多学知识解答试卷试题,甚至能够启发自己得思维在实践生活中予以应用.