基于ELM优化PI+重复控制策略在APF中的应用研究

赵宇明 何新华 孟 亨 李 鑫

1(广东华晟安全职业评价有限公司 广东 广州 510650) 2(辽宁工程技术大学电气与控制工程学院 辽宁 葫芦岛 125105)

0 引 言

非线性负载的广泛应用，严重影响电网电能质量，使电网电流中存在大量谐波，有源电力滤波器(Active Power Filter,APF)可有效解决此问题[1-2]。针对APF的电网谐波补偿问题，国内外学者进行了大量研究，提出了相应控制策略。谈竹奎等[3]提出将半桥MMC应用在APF中，并重点研究了特征次谐波补偿控制策略，补偿效果明显。乔鸣忠等[4]结合重复控制与PI控制提出一种新型的复合控制策略。孙龙庭等[5]提出了针对控制环路切换和相位锁定的优化方法，并引入了一种与传统重复控制相比具有6倍响应速度的T/6重复控制方法抑制谐波电流。汪玉凤等[6]为减小IGBT故障对多电平级联H桥(CHB)逆变器运行稳定性的影响，提高级联APF系统的故障容错能力，提出多电平CHB逆变器开路故障检测与3N+1冗余容错策略。谭兴国等[7]提出一种基于元件冗余的三相四开关容错型APF，针对三相六开关APF的故障判别，应用功率器件承受电压变化识别桥路开路故障。

综上，目前模块化多电平换流器(Modular Multilevel Converter,MMC)在APF中应用提高了其补充效果，并可以适应非线性负载高电压大功率电网环境。鲜有采用重复控制策略应用在基于MMC结构的APF中，本文提出一种基于ELM优化PI+重复控制策略应用在基于MMC的APF谐波抑制控制中，并进行实验验证。

1 MMC-APF拓扑结构

图1为MMC-APF系统模型，该模型主要由谐波的检测部分和补偿电流电路部分组成[8]，MMC拓扑结构如图2所示。工作原理如下：采集非线性负荷中的谐波电流分量，通过谐波检测电路生成响应的指令信号，进而生成CPS-SPWM调制波，作为基于MMC结构的IGBT触发信号；控制MMC电路生成补偿电流，进行谐波抑制。

图1 MMC-APF原理框图

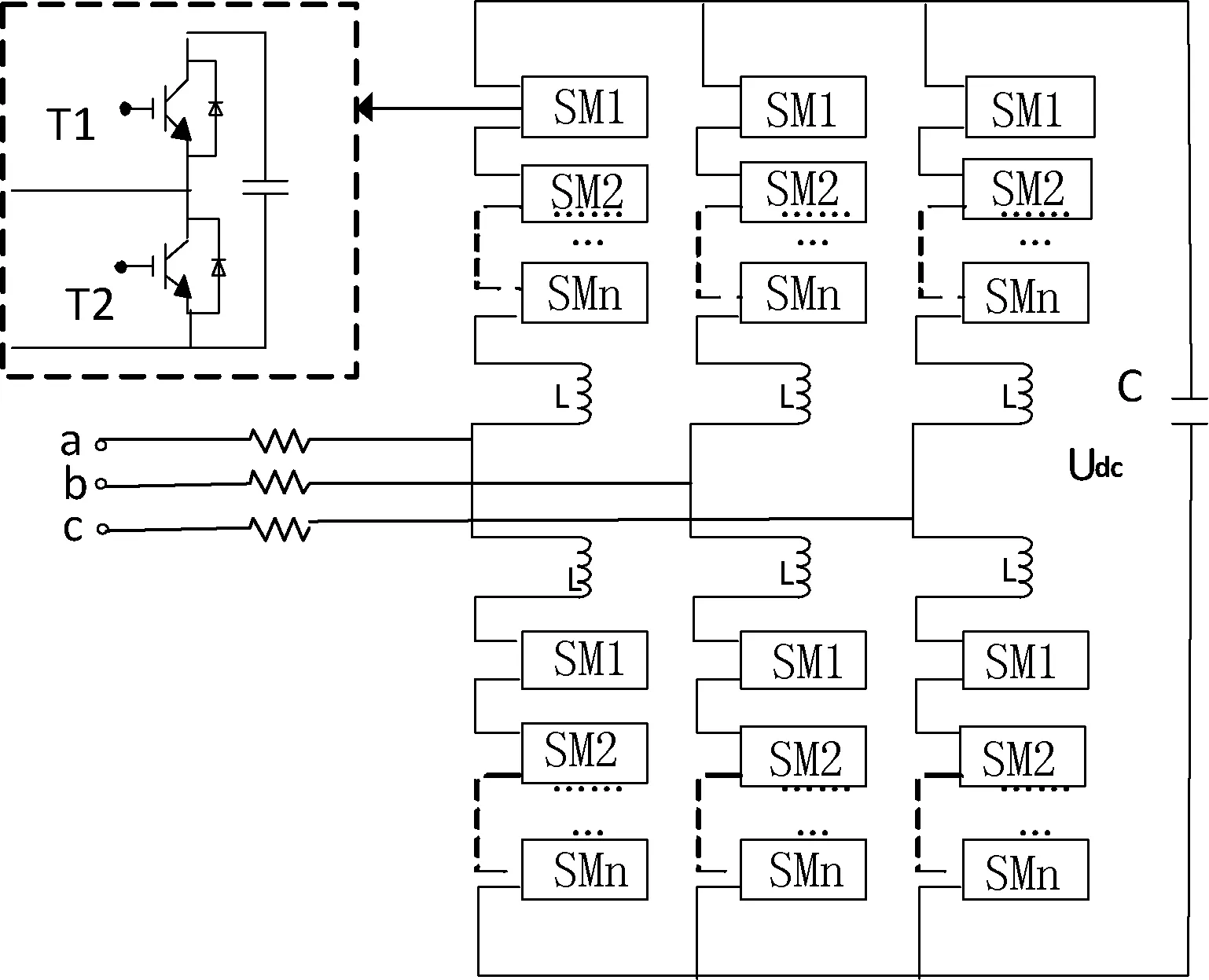
图2 MMC及其子模块拓扑结构

2 基于ELM优化的PI+重复控制策略

图3为PI+重复控制策略原理框图，其中：r(k)为其系统的输入信号；z-N为周期延时控制环节；Kr为重复控制增益，用以调节控制器的稳定裕度以及误差收敛速度；zk是超前环节，用来补偿因被控对象和滤波器导致的总相位滞后；s(z)为低通滤波器，校正中低频段的畸变波形，补偿谐振峰，从而保证系统的稳定性；Q(z)为滤波器；Gp(z)为稳态滤波器；y(k)为输出信号。该策略可较好地解决传统PI控制跟踪误差较大而重复控制对于突变负载跟踪能力不足的问题[4,9]。

图3 PI+重复控制框图

图3中PI控制器和重复控制器分别表示为：

(1)

(2)

其复合控制跟踪误差与特征方程为：

(3)

(4)

由式(3)、式(4)可知，PI+重复控制的稳定首先需要PI控制器稳定，同时需保证D3(z)=1+[z-1D1(z)+D2(z)]Gp(z)的根是在原点为圆心的单位圆中。

由于采用PI+重复控制时，传统PI控制的两个参数多为经验法确定，且不能实时整定，易造成当负载进行突变时，不能进行很好的补偿，同时仅采用PI+重复控制时控制的精度不能达到所要求的精度，故提出采用极限学习机ELM算法对此控制策略进行进一步优化。其中ELM神经网络根据系统的运行状态，通过自学习与权值调整，实时地对PI参数Kp、Ki进行整定，以提高系统性能。

该网络模型的输出误差为：

(5)

式中：ωi为第i个输入层节点与隐含层节点间的权值；bi为第i个输入层节点与隐含层节点间的偏置；βi为第i个隐含层与输出层间的连接权值；gi为隐含层激活函数；x为输入样本；yi为输出样本。

隐含层输出矩阵为：

(6)

可得：

e=‖Hβ-T‖

(7)

其中：

经过极限学习机的不断学习优化，误差e不断减小，e=0为无误差。由于H不存在逆矩阵，无法进行求解，采用Moore-Penrose广义逆矩阵H+进行求解：

β=H+T

(8)

ELM算法与PI重复控制的结合框图如图4所示。优化算法具体流程如下：

(2) 确定ELM神经网络输入层节点数、输出层节点数、激活函数g(·)，并初始化ELM神经网络隐含层神经元个数j=1。

(3) 确定输入向量样本维数，若维数过多，则采用PCA降维算法进行降维处理。

(4) 设定每次循环隐含层神经元个数j=j+1。

(5) 将PI控制参数Kp、Ki值作为输出，进行ELM神经网络训练，并利用式(5)计算当前时刻误差e(k)。

(6) 若e(k)小于设定误差阈值，则结束循环；否则，转入步骤(4)。

(7) 输出最优控制参数Kp、Ki，并计算经PI控制器调整后的输出值i(k):

i(k)=i(k-1)+Kp(e(k)-e(k-1))+Kie(k)

(9)

图4 ELM优化PI+重复的控制结构

3 仿真研究

为验证所提控制策略的可行性，基于CPS-SPWM调制策略，搭建模块化五电平APF仿真模型，仿真系统的主要参数如表1所示。

表1 仿真系统参数表

图5至图7分别为传统PI控制、PI+重复控制、ELM优化PI+重复控制补偿后的电流波形图以及频谱图。经传统PI控制，所得波形THD为8.24%，经PI+重复控制，所得波形THD为6.37%，而采用ELM优化的PI+重复控制时所得波形THD为3.25%，谐波含量值较传统PI控制减少4.99个百分点，较PI+重复控制减少3.12个百分点。由此可见，所提优化控制策略可显著减少电流谐波含量。

为验证ELM神经网络在优化算法上的优越性，分别对基于BP神经网络、粒子群(PSO)优化的BP神经网络、遗传算法(GA)优化的BP神经网络以及所提ELM神经网络的PI+重复控制算法进行对比分析，其仿真性能对比如表2所示。

表2 神经网络算法性能对比

通过谐波含量与电流跟踪误差的分析可知，经ELM优化的PI+重复控制算法电流跟踪误差较其他算法相比性能略有提高；通过响应时间的对比可发现，所提基于ELM的算法在学习速度上显著高于其他几类优化算法。这是由于传统BP神经网络学习过程中需要不断迭代更新权重和阈值，使得运算出现易陷入局部极值且训练速度慢等问题。而PSO-BP与GA-BP算法皆是对BP算法进行改进，通过寻优算法寻找BP神经网络的最佳权值与阈值，虽然在一定程度上加快了控制器响应时间，但仍存在权值阈值调整的问题。ELM算法可随机产生输入层与隐含层间的连接权值及隐含层神经元的阈值，且在训练过程中无须调整，只需设置隐含层神经元的个数，便可获得唯一的最优解。

4 实 验

为进一步验证所提控制策略的实用性，根据表3所示参数，搭建如图8所示实验平台。基于MMC结构的APF的主要是由以下几部分组成：MMC主电路、信号采集电路、主要的控制电路、IGBT驱动电路。

表3 MMC-APF实验参数

图8 MMC-APF实验平台

图8中：1、2是MMC的上下桥臂模块，每个上桥臂由2个子模块组成，每个子模块由一个型号为BSM100GB60DLC的IGBT和型号为日立450 V电容组成，每个模块中电容连接在IGBT的2和3引脚上；3是电流互感器和电压互感器以及信号调理电路，其中电流互感器是型号为CHB-25NP的宇波模块，电压互感器的型号为CHV-400VB；4是IGBT触发电路每个触发电路驱动板可以触发6个IGBT；5是MMC模块中上下桥臂的电感；6是DSP2812控制板和AD模块电路板；7是示波器，示波器显示的是经过补偿后的电流波形；8是整流和负载部分。

图9为没有进行补偿之前的负载电流波形图，由于非线性负载的存在，系统中存在谐波，导致电流波形非正弦波。图10为采用ELM优化PI+重复控制策略后的补偿后负载电流波形，波形接近正弦波，满足系统要求。此外，图11为补偿前后的负载电流FFT结果对比，可以看出，经所提策略补偿后的电流谐波含量从27.04%下降到4.27%达到电网要求，降低22.77个百分点，补偿效果显著。

图9 补偿前负载电流实验波形

图10 补偿后电网电流实验波形

图11 补偿前后电流FFT对比图

5 结 语

1) 分析电流内环PI+重复控制模型，提出以监测电流的实际值、参考值、误差值为输入，以PI控制器的两个参数Kp、Ki为输出，采用ELM优化PI+重复控制的控制策略。

2) 基于CPS-SPWM调制策略及所提控制策略，构建基于5电平MMC的APF仿真模型。对优化前后控制策略进行补偿波形的比较，优化后的控制策略所得负载电流THD较传统PI控制减少4.99个百分点，较PI+重复控制减少3.12个百分点，补偿效果明显。

3) 对基于BP、PSO-BP、GA-BP与所提ELM神经网络优化的PI+重复控制策略进行仿真对比，结果表明，所提算法在误差精度、响应速度、补偿后电网电流谐波含量等性能上较其他算法有显著优势。

4) 基于所提控制策略，搭建基于5电平MMC的APF实验平台，实验结果表明，采用所提控制策略补偿后的电流谐波含量较补偿前降低了22.77个百分点，验证了该控制策略的实用性。