基于多目标遗传算法的柴电混合动力船舶功率分配优化

张 程 贾宝柱，2* 邹佳奇

1(大连海事大学船舶电气工程学院 辽宁 大连 116026)

2(广东海洋大学海运学院 广东 湛江 524088)

0 引 言

混合推进船舶(Hybrid Propulsion Vessel-HPV)指单船包含两种或两种以上的动力形式，如液压-电力推进方式[1]、风帆助航推进[2]、喷水推进[3]，以及柴-电混合推进[4]等。柴-电混合系统是混合推进系统的主要形式之一，在传统柴油机直接推进系统的基础上增加了电力推进方式以提高船舶的操控性能，既能利用操纵性好、噪音低的柴油发电机作为动力源，又可以兼顾柴油推进装置单机功率高、输出扭矩大的优势。混合推进系统控制问题主要研究如何改善多种工作模式下功率配置方案，在满足动力需求的前提下实现降低燃油成本、减少排放、提高船舶经济性的目的。

混合动力船舶与混合动力汽车在动力形式上非常类似，本质都是通过利用多种动力源(柴油机、汽油机、蓄电池等)驱动船舶或汽车的工作运行。目前，国内外专家学者对于混合动力汽车的相关研究已经颇有成果，这对于研究混合动力船舶有一定的借鉴意义[5-10]。在船舶相关的研究中，Zahedi等[11]考虑了船舶在多种工况下的电力负载变化，提出了一种最小化燃油消耗率的控制策略，根据船舶航行平均需求功率和功率变化特性去制定发电机组的工作准则，使其工作在最优工作状态，优化后的带有储能装置的直流电力系统与交流系统相比，显著地降低了燃油消耗。Mahdi等[12]采用带有约束条件的粒子群优化算法，设计了由原动机、发电机组等动力源的最优输出功率组合。

本文以深水三用工作船(Deep Water Anchor Handling Tug Supply Vessel, DW-AHT)混合动力系统为主要对象，研究其在不同工况模式下的动力系统最优分配方案，以满足动力系统节能及低排放的多重指标要求。不同于一般的客船或货船的性能需求，深水三用工作船要兼顾航行、定位和拖带等工况模式。本文以节能和排放作为目标参数，采用多目标遗传算法NSGA-II与混合整数规划相结合的方法，合并所有的Pareto最优解，得到合并的Pareto前沿。之后利用模糊决策方法，为每种工作模式选出最优动力分配方案。本文试图得到可用于优化实际船舶动力分配的相关理论依据，进而达到提高船舶经济性、降低环境影响的目标。

1 混合动力推进系统模型

深水三用工作船推进系统由两台独立操作的主柴油机直接驱动的舵桨推进系统、两台电力驱动的全回转推进器和三台侧推构成，如图1所示。动力系统包括两台主机SG1、SG2和4台柴油发电机组DG1-DG4，通过各自的主开关为高压母排Bus1和Bus2供电，两台全回转推进器M6、M7分别连接至Bus1和Bus2，为实现分区供电，两端母排之间由区联开关隔开。M4、M5两台艏侧推和M3艉侧推可为船舶提供侧向推力，主柴油机主要用于驱动#1和 #2主推进器，还可以带动轴带发电机SG1、SG2为母排供电。推进电机M1和M2通过#1和 #2主齿轮箱驱动相应的主推进器。各推进器的位置通过以船舶型心为原点，右舷方向为Y轴正向的坐标值表示，具体如图2所示。

图1 深水三用工作船动力系统结构图

图2 推进器布置图

动力系统可以分别工作在PTO(Power Take Off)模式、PTH(Power Take me Home)模式和BOOST模式下，对应船舶的不同推进工况要求，如表1所示。PTO模式即为轴带发电机模式，此模式下由主柴油机驱动主推进器做功，同时剩余功率驱动轴带发电机SG1、SG2发电为船舶电网供电。PTH模式和BOOST模式通常被称为PTI(Power Take In)模式。PTH模式适用于低航速航行工况，此时船舶所需推进力较小，主柴油机不工作，轴带电机此时作为电动机，驱动主推进器。BOOST模式也称为助力模式，当主柴油机直接驱动螺旋桨所产生的推力不能满足要求时，推进电机在柴油发电机提供的电能驱动下，通过齿轮箱可以进一步提高主推进器的推进功率。

表1 动力系统工作模式

2 目标函数

2.1 混合推进系统燃油消耗成本

对在正常工作状态下的船舶来说，混合推进系统的燃油消耗成本包括主机油耗成本和发电机组油耗成本。主机和发电机组的原动机都属于柴油机，柴油机的每小时燃油消耗量曲线可近似用一个关于负荷的二次多项式函数来表示：

(1)

式中：g(Pi)为第i台柴油机每小时的燃油消耗量，单位为g/h；ai、bi和ci为第i台柴油机的多项式系数；Pi是第台柴油机的负荷功率，单位为kW。

燃油消耗率是指柴油机每小时、每单位功率的燃油消耗，表示为：

(2)

根据相关技术手册，主机一般使用重油，发电机组使用轻柴油，考虑两种燃料的价格不同，柴油机的油耗成本可以表示为：

(3)

混合推进系统燃油消耗总成本可表示为：

(4)

式中：F(Pi)为混合推进系统燃油消耗成本，单位为美元/h；N为柴油机台数；si为第i台柴油机的运行状态，运行时si=1，否则为0；Costi为第i台柴油机消耗的燃油价格，单位为美元/t。

2.2 污染气体排放量

船舶在海上航行时，需要控制污染气体的排放，以减小空气和海水污染。本文选取船舶排放气体中的氮氧化物NOx为目标。柴油机的每小时NOx排放量曲线可近似用一个关于负荷的二次多项式函数来表示：

(5)

式中:e(Pi)为第i台柴油机每小时的排放量，单位为g/h；αi、βi和γi为第i台柴油机的排放多项式系数。则船舶每小时NOx排放总量E(Pi)(单位为t/h)可表示为：

(6)

3 约束条件

3.1 柴油机发力约束

在正常工作条件下，对不同的柴油机应该设置不同的运行功率限制，以防止超负荷或运行在过低负荷，对其造成损伤。

(7)

3.2 船舶功率平衡约束

若不考虑系统的功率损耗，船舶混合动力系统发出的功率应该与船舶所需功率相平衡。船舶所需功率Ptotal包括用于推进的功率Pprop和供给用电负载的功率Pelec两部分，表示为:

(8)

3.3 推进电机功率约束

发电机组输出的功率包括用于推进的功率和用于发电的功率。发电机组用于推进的功率应不超过推进电机能输出的最大输出功率。另外在极限情况下，假设用于发电的功率全部由发电机组承担，则有：

(9)

4 多目标遗传算法及模糊决策

遗传算法(Genetic Algorithm，GA)是通过借鉴进化生物学中的诸如遗传、突变、自然选择、杂交等现象而发展完善的进化算法[13]。遗传算法能够在搜索过程中通过上述现象进行进化，自适应地控制搜索过程，并获得最优解。在之后的发展中，非支配排序遗传算法(NSGA)在解决多目标的问题上非常有效，一般用来解决多目标优化问题。优化问题的解一般为一组解，为了得到最终符合决策者的解，采用模糊决策进行最终解的决策。

4.1 多目标遗传算法

在多目标优化中，目标间可能存在相互制约的关系，改善某个目标将会使其他目标恶化，因而问题的解常用帕累托(Pareto)前沿来表示，在Pareto前沿上的解称为非支配解。要获得非支配解，首先比较并判断对种群中的个体的支配关系。任意选取两个个体p和q，进行以下判断：若pq，则把p加入到受q支配的集合Sq中，同时p的被支配数增加1。循环进行直到种群内的所有个体都两两比较完毕。之后再遍历一遍种群，判断其中每个个体的被支配数，若为0，说明该个体不受其他任何个体支配，即为一个非支配解。

根据混合动力船舶动力系统的工作特点，本文采用非支配排序遗传算法NSGA-II来求解Pareto前沿。NSGA-II是在NSGA的基础上改进得到的一种多目标进化算法(Multi-objective Evolutionary Algorithm, MOEA)，采用了快速非支配排序和精英策略，可以加快搜索过程中的收敛速度，并对秩相同的个体根据排挤机制选择保留，有效地保护最优解的多样性。

完整的非支配排序多目标遗传算法(NSGA-II)步骤如下：

Step1随机产生初始化种群P0，种群大小为N，并计算种群内个体的适应度，将进化代数设置为t=0。

Step2对初始种群P0进行非支配排序，每个种群的适应度即为其非支配水平，通过排序，每个个体得到一个RANK值，并计算拥挤距离。

Step3通过竞赛法选择精英个体，并通过交叉、变异操作，生成一个种群大小同样为N的子代种群Q0，并再次计算适应度作为非支配水平。

Step4将子代种群Ot和父代种群Pt合并，得到一个种群大小为2N的新种群Rt。

Step5对Rt采用拥挤比较算子排序，依次选取排序最优的个体复制到新的种群Pt+1，直到新种群规模为N，此时为一次循环，循环代数t加1。

Step6判断是否达到最大迭代次数tmax。若不满足则重复Step3-Step5，直到满足条件，算法停止。

算法流程图如图3所示。

图3 非支配排序多目标遗传算法流程

4.2 约束处理

在求解具有约束的优化问题时，会出现能否收敛到全局最优解的问题，没有约束的优化问题则不会。约束条件的产生会导致在种群进化的过程中产生不满足约束的一些个体，所以需要对约束进行处理，保证算法的正确性。

由于在NSGA-Ⅱ算法中采用锦标赛选择算子，存在对种群中的个体两两比较的过程，借此过程，可以确定两个体之间的约束对比情况，采用约束支配的定义处理约束条件[14]。

当以下任意条件成立，称解p约束支配q。

(1)p为可行解，q为不可行解。

(2)p和q都为不可行解，但p具有更小的约束违反程度。

(3)p和q都为可行解，且p支配q。

约束违反程度函数可定义为：

(10)

式中：约束条件gi(X)和hj(X)满足条件：gi(X)≥0，hj(X)=0；gi(X)表示当gi(X)≤0时返回0，而当gi(X)>0时返回|gi(X)|。即满足约束的条件下，约束违反程度等于0；不满足约束时，约束违反程度大于0。可以得到的结论是，任意可行解的RANK值都比不可行解的RANK值低，而在两个不可行解中，约束违反程度小的RANK值更低。因此，采用这种约束处理方法使得可行解更容易被选中，而不可行解会在进化过程中被逐渐抛弃，且无须自定义参数。

4.3 模糊决策

模糊性是人类思维和客观事物普遍存在的属性之一，而模糊集合论则是处理模糊现象的有效工具。模糊决策正是模糊集合论与决策理论相结合的产物[15]。

运用NSGA-Ⅱ算法可以得到所有满足约束的船用主机和发电机组需要发出的功率值，即由算法求得的Pareto前沿，为一组解。理论上，这组解全部可以被认为是当前约束条件下的最优解。通过模糊决策的方法，可以从这组最优解中，选取最符合决策者目的的折衷解。对一组Pareto前沿的最优解进行模糊化处理，其隶属函数表示为:

(11)

式中：μi是模糊化后的目标函数;fi是最优解的第i个解;fi,min是最优解的最小值;fi,max是最优解的最大值。

之后，把燃油消耗成本和污染气体排放量作为因素集，对在某确定工况下的最优解作因素评价，构成模糊评价矩阵。需要说明的是，因素评价矩阵的设定会受到人为主观因素的影响，设定的值可以根据决策者的倾向和意图来改变。为了便于计算和考虑仿真的真实性，对于本文仿真需要的混合动力船舶的四个工作条件，将进行模糊化处理后的隶属函数进行线性化的因素评价，评价矩阵在表2中给出。

表2 典型工况模糊评价矩阵

5 仿真计算及结论

5.1 仿真参数

DW-AHT有六个柴油发动机，其中有两个主发动机、三个发电机和一个备用柴油发动机。具体参数见表3。为了保证仿真工作的真实性，在仿真过程中，船舶主发动机和发电机的工作负荷范围规定在30%～100%之间。在船舶运行过程中，如果两台主发动机或两台以上的发电机同时运转，根据船用柴油机的工作特性，应确保其原动机负荷相同。

表3 船舶主机和柴油发电机主要参数

船舶匀速航行中，螺旋桨推力和船舶所受阻力平衡。可以通过计算航行时所受阻力可得到螺旋桨后功率，考虑机桨功率传递效率，进而可得到所需推进功率[16]。船舶在航行中所需总功率为推进所需功率和船上其他负载所需功率之和。本文考虑该深水三用工作船在某一次出行任务中分别经历的拖带(T)、动力定位(DP)、全速航行(FS)、靠港停泊(HB)四种典型工况下的功率分配问题。四种工况下的所需功率经过计算后如表4所示，为方便计算，每种工况下所需的电力功率假定为定值，且只受工况变化的影响，计算方式根据查阅该船电力负荷表计算得出。

表4 典型工况所需功率

假设船舶在某一天12小时的工作状态和速度为：靠港停泊(HB)2小时后，以全速(FS)航行4小时，平均速度为18节，到达海上某个地方后，进行动力定位(DP)3小时，最后以100吨的牵引力，在拖曳(T)工况下，以8节的平均速度航行3小时。具体的航速变化如图4所示。

图4 航速随时间变化图

5.2 仿真计算

图5-图8分别为使用NSGA-Ⅱ算法针对5.1节中提出的典型工况进行的计算，得到最终的Pareto前沿。在全速航行和拖带工况下，相对连续和平滑的曲线为所有最优解组成，组成曲线的每一个点都是一个Pareto最优解，代表一个有效方案。靠港停泊和动力定位工况下的Pareto前沿是一个或几个散点，每个点都代表一种有效的解决方案。通过使用模糊决策算法，可以在这些Pareto前沿中选择最符合决策者要求的解。最终结果见表5。

图5 靠港停泊工况下的Pareto前沿

图6 靠港停泊工况下的Pareto前沿

图7 动力定位工况下的Pareto前沿

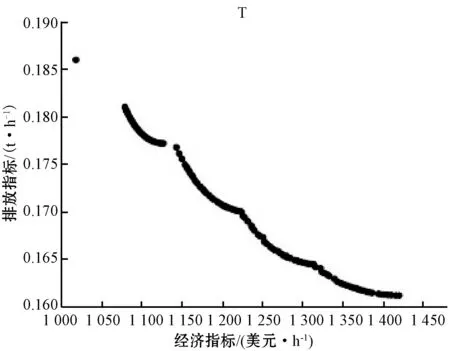
图8 拖带工况下的Pareto前沿

表5 对Pareto前沿模糊决策后的最优解

若在每种工况下进行单目标的优化计算，可以获得该目标的最佳值。若两个目标同时作为目标函数，则两个目标不可能同时达到最小值，而是一个折衷解，这也正是多目标优化算法的作用。表6为只把燃油成本作为目标优化的单目标优化结果，此时的污染气体排放不再作为目标和约束条件，进行计算所得结果。

表6 以燃油成本为单目标优化的结果

对两次结果进行分析，以拖带工况为例，如果只考虑经济指标，单目标优化后的最优值为1 020.3美元/h，相应的排放指标为0.183 9 t/h，此时燃料消耗量为低。应用多目标优化算法后，优化得到的经济指标最优值为1 018.2美元/小时，最优排放指标为0.186 0 t/h。可以看出，燃油消耗和排放指标，不能同时“完美”降低，污染气体排放目标和燃油成本的目标，基本满足“一升一降”的趋势。在动力定位的工况下，若只考虑船舶的整体经济性，燃料成本可以降低至404.4美元/h，但与经过了多目标优化和模糊决策后的结果相比，污染物的排放增加了接近1.6倍。以上结果表明，将多目标优化模型应用在柴电混合动力船舶功率分配的问题上，能够在考虑经济效益的同时减少污染，给出最合适的方案。

6 结 语

本文研究了针对柴电混合动力船舶的功率分配的优化问题。在混合动力船舶中，主柴油机和柴油发电机组都可以为船舶负载提供功率，以此建立柴油机燃油消耗成本和污染物排放为目标的多目标优化问题，根据混合动力船舶工作特点，在约束条件中，引入系统功率平衡和柴油机发力约束，用NSGA-Ⅱ算法解得Perato前沿，再用模糊决策的方法解得最优解。通过MATLAB仿真验证，得到以下结论：

(1) 针对柴电混合动力船舶所建立模型合理有效，能够应用于在多目标条件下的求解混合动力船舶功率分配问题。

(2) 运用NSGA-Ⅱ算法和模糊决策相结合的方法能够较好地解决多目标优化问题，可以兼顾船舶经济指标和排放指标，在一定程度上提高船舶能效。