基于简易装置的空气柱共鸣的声速测量实验

翦知渐，周艳明，谢 中

(湖南大学 物理与微电子科学学院 大学物理实验中心，湖南 长沙 410082)

“互联网+”时代大学物理实验课程的教学模式有了很多变化和发展[1，2].目前各大MOOC平台上有很多高校都开设了大学物理实验课程，作为线下课程的一种有益补充发挥了很好的作用[3-5].同时，线下课程的教学也大量融入了线上教学的元素，虚实结合的教学模式已成为物理实验教学的新方向[6，7].一直以来，大学物理实验的MOOC课程的实验操作部分主要是以虚拟仿真实验为载体，而虚实结合教学模式的实验操作部分基本上是在实验室环境中完成的，所以要在学生动手能力培养等方面满足课程教学大纲的要求仍旧离不开实验室的基础环境.如何使实验课程的远程教育发展得更均衡、更有效力，是物理实验教学的从业者们需要思考的问题，而今年的新冠疫情使得全世界的实验课程教师都直接面对了这一问题，很多人都给出了各自的解决方案——“宅+实验”[8]，这些教学方案在实际教学过程中发挥了巨大的作用，也取得了很好的效果.

湖南大学物理实验中心设计了一系列的居家实验项目，再加上虚拟仿真实验，基本可以替代实验室环境下的实验教学.这些实验方案的设计基于居家环境下随手可得的实验器材，不以精确测量为主要目的，侧重于对学生实验方案设计能力、动手能力、数据处理能力的训练.因为实验条件的限制，实验结果可能误差较大，但通过分析实验的物理过程，控制实验条件或改进实验方案，都可以有效提高实验结果的精度，这个过程对于培养学生的实验素养是很有益处的.

本文讨论其中的一个项目“空气柱振动的频率特性”，并对实验过程中的一些影响因素进行分析，消除系统误差后，声速的测量结果在误差范围内与标准值符合.

1 实验原理与实验方案

1.1 实验原理

本实验的研究对象是空气柱振动发声时的共鸣现象.声波在一顶端开口、底端封闭的均匀圆柱形容器中传播时会在底部被反射，容器中的声场实际上为入射波与反射波的叠加，如图1(a)所示，声源频率合适时，将形成稳定的驻波.瓶底反射处是刚性反射面，因而形成波节.如果瓶口处正好是波节，则该处空气的振幅基本为零，对向外发出的声音没有贡献，此时听到的声音就会比较小；如果瓶口处是波腹，则对外发出的声音将会增强出现共鸣的现象，波幅增加一倍，声强增加到四倍.所以，如果声源是多频率混合的，容器会有“选频”的作用，符合共振条件的音频将会被放大.

图1 管状容器中声波的共振

因为相邻的波节与波腹的间距是λ/4，所以能产生共振的最长的波长是4L，如图1(b)所示的半个驻波；每当波长满足L=λ/4 +nλ/2(n为任意非负整数)时，都将会产生共振.因此，最长波长4L对应的频率f(f=c/4L，c为空气中的声速)称为基频，相应的3f、5f、7f……是泛音频率.空气柱对外传播的声音是一个复音，基频决定了空气柱发声的音调，泛音决定了它的音色.

当向容器中注水时，声源实际上是水流撞击水面发出的声音，这个声音里面包含的频率非常丰富.频率不符合共振条件的声音，将很难传出容器，而频率符合共振条件的声音将会被放大，所以听到的声音基本上只有符合共振条件的音频.注水的过程中，空气柱的长度将会逐渐缩短，也就是共振的波长越来越短，所以听到的声音其音调越来越高.

设空气柱的长度为L=L0-βt，这里L0是测量开始时空气柱的长度，β是均匀注水时瓶中水面上升的速度.因此听到的声音频率(基频)将会是

(1)

由实验测出注水过程中声音频率的变化，对实验数据进行适当处理后，声音频率的变化应该能满足式(1)，并可由此求得声速值.

1.2 实验器材与实验步骤

准备一细长、均匀的圆柱形透明容器(细长的瓶子或水杯)；米尺；胶带；一部下载了Phyphox APP软件的智能手机(图2).在接近容器底部的位置做一水平标志并测量其到顶端的距离L0(主要是防止容器内的底部不够平整)，打开水龙头往容器中匀速注水，控制流速使得容器注满水的时间至少为30秒(但要保持水流连续).然后用手机秒表功能测量水面高度从底部标志线增涨至瓶口时所需的时间t0，则可得β=L0/t0.

图2 实验所用器材：细长容器、米尺、胶带、智能手机

保持水的流速不变，清空容器，准备开始实验.打开手机App Phyphox的“Frequency history”功能模块，水面高度到达底部标志线时开始测量，Phyphox将会记录每个时刻接收到的声音频率，数据还会以图形的方式实时显示在屏上.数据记录界面如图3所示.水面快接近瓶口时停止测量，在菜单栏中选择“Export Data”导出数据.

图3 Phyphox的数据记录界面

2 数据处理

首先观察数据记录的图形，如图4所示.“Frequency history”功能模块的采样周期是0.04545s，采样频率约22Hz，使用不同的容器、不同水流速度进行的实验，其记录的数据分布会有较大差别.为什么会出现这种情况？

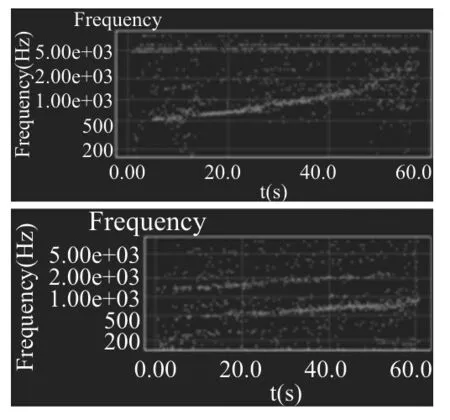
图4 两次不同的实验，记录数据显示的图形

因为APP是先对接收到的声音信号作频谱分析，在采样的那个时刻，APP所记录的频率是该时刻声音频谱中强度最大的频率分量.因为水流速度不同、容器材质不同、周围环境不同等都会使得声音的频谱不一样，因而各时刻采集到的声音频率就会不一样，其中会包含基频f的声音、泛音3f甚至5f的声音，还有环境噪音.因为水流较小声音低沉，而且高频声音易于衰减，所以数据记录中基频的数据点最多.可以看到，基频带是位于数据图下方的那条较粗的数据带，其他的则是噪音和泛音的数据点.

将数据导入Origin并作出频率值的散点图，图5是某次测量的数据.因为数据记录中基频的数据点最多，形成了带状，所以对数据的处理主要是针对基频带的数据进行分析，因此要将基频带之外的数据点排除，利用Origin的“屏蔽数据点”功能即可做到这一点.对屏蔽处理后的数据点进行非线性拟合，结果如图6所示.

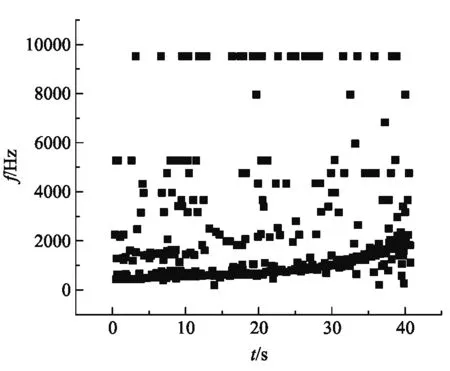
图5 频率记录值的原始数据散点图

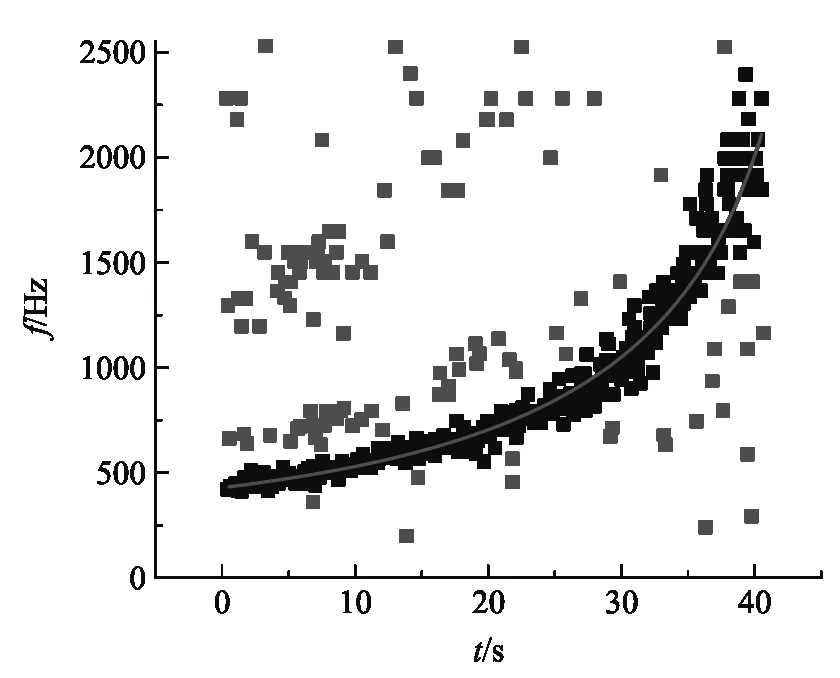
图6 基频带数据点.红色的数据点是被屏蔽的非基频点，红色曲线是对基频带的非线性拟合结果

根据频率随时间的变化关系式(1)，非线性拟合所采用的函数表达式为

(2)

比较式(1)和式(2)，可以得到对应关系：a↔ 4L0/c，b↔-4β/c.

图6中的数据其拟合结果为：参数a=0.00234，b=-4.588×10-5，COD=0.95974.可以看到，对于非线性拟合而言，拟合曲线与实验数据符合得还是相当不错的.

声速的计算：因为是基频带，故声波波长为λ(t) = 4(L0-βt)，所以我们得到声速为

(3)

将测得的初始参数L0和β代入，可得到时刻ti的波长λ(ti)，从拟合曲线中可得到时刻ti的频率拟合值f(ti)，因此有

(4)

N为有效数据点的个数.图6的这组数据中，L0= 0.178 m，β=0.003765 m/s，利用式(4)计算可以得到c= 303.5 m/s.

作为比较，测量时室温下的标准声速值约为338.9 m/s.从结果中可以看出，测量值与标准值有较大偏差.

3 对测量结果的分析和修正

利用空气柱共鸣演示共振现象，并用于测量声速的实验多见于报道[9-11]，但相关研究基本上只给出了实验方法，并未对结果进行分析.一般来说，测得的声速与标准值比较其偏差基本在容许范围之内.

本实验方案所得结果与标准值相差颇大(10.5%)，已超出了正常范围.虽然简陋的测量条件会带来较大的误差，但这里长度的测量误差小于2%，时间的测量误差在2%左右，即便再考虑其他因素带来的误差，测量结果的偏离也不应该有如此之大，一定存在某种系统误差.

3.1 L0的修正值

在本实验中，因为管长较短，声波传输的阻抗特性带来的影响不能忽略，由此产生的误差必须考虑.设管长为L，管半径为r，声波波数为k，管底(x= 0)为声源，其阻抗为Z0；管口处(x=L)阻抗为ZL，有如下关系[12]：

(5)

其中S为管横截面积(πr2)，ρ0、c分别为空气密度与空气中的声速.

因为管口是开放的，存在声辐射，所以其阻抗为辐射阻抗[12]：

ZL=ρ0cS(R1(2kr)+jX1(2kr))，

R1(x)=1-2J1(x)，

X1(x)=2H1(x)/x

(6)

其中J1为一阶Bessel函数，H1为一阶Struve函数.当频率较低时(kr<<1)，上式简化为

(7)

实际上只要kr<0.5上式即可成立.

空气柱共振的条件是Z0为一个纯粹的声阻(虚部为零)，将式(7)代入式(5)，在kr<<1的条件下可得共振条件为

tan(nπ-kL)=(8/3π)kr≈tan(8kr/3π)

(8)

ΔL=8r/3π ≈ 0.85r

(9)

称为末端修正或管口修正，这个现象相应地也称为管口效应.

图6的实验数据中，所用容器的管口直径为0.048 m，因此ΔL= 0.0204 m，ΔL/L0超过了11%，可见末端修正带来的影响很大.

实际上末端修正可以很容易用实验证明：将实验用的容器清空，放入一个连接了可调节频率的音频发生器的小手机耳机(如使用手机App如Frequency Sound Generator作为音频发生器).开始时容器内的耳机声音很小，实验者很难听到，当改变频率至最低共振频率时，实验者即可听到明显的共鸣声.从测得的最低共振频率可以计算出波长，从而得到空气柱的长度.实验结果证实，末端修正基本是正确的.

见于文献报道的其他类型空气柱共鸣的实验中，因为空气柱较长而管直径较小，而且测量的往往是高于基频的共振频率，因此管口修正带来的影响较小，一般都忽略或归入了测量误差.本实验是在简陋环境下进行的，一般使用的都是短而粗的容器，所以管口修正带来的影响就不能忽略.

3.2 β值对结果的影响

β是一个测量值，其意义为管中水面上升的速度，看起来似乎与管口效应无关，但从前面的分析中可知基频的波长表达式为4(L0-βt)，所以β真实的意义是“空气柱长度”缩短的速度，而空气柱的长短是与末端修正有关的.

实际上，在3.1中计算管末端的阻抗ZL时，是在低频近似下(kr<0.5)得到表达式(7)的，当频率逐渐升高的时候这一点并不能总是被满足.如图7所示[12]，当频率较高时管末端阻抗ZL的实部R1增加得很快，虚部X1也不再近似满足与kr的线性关系，随着kr的增加X1是一个逐渐减小的振荡.因此高频时管口效应带来的影响是很复杂的，固定不变的末端修正公式(9)不再适用.因此空气柱长度的变化不仅与β有关，也与末端修正值随时间(频率)增加而引起的变化有关，这实际上也就意味着β不再是一个常数，而与时间有关.

图7 辐射阻抗的实部和虚部随x变化的关系曲线.R1为实部，X1为虚部，其中x = kr

另一方面，β作为测量值是一个常数，在公式中也是一个常数参量.声速计算公式(3)是时间的非线性函数，计算结果对β的变化非常敏感.如图8所示，如果输入不同的β值，声速的计算结果随时间的变化趋势可能完全相反.图8中两条曲线显示的是在测量水面上升速度β时，水面升至瓶口的时间仅仅相差±0.9 s的结果，这样的误差在手动测量时间的时候很容易产生.

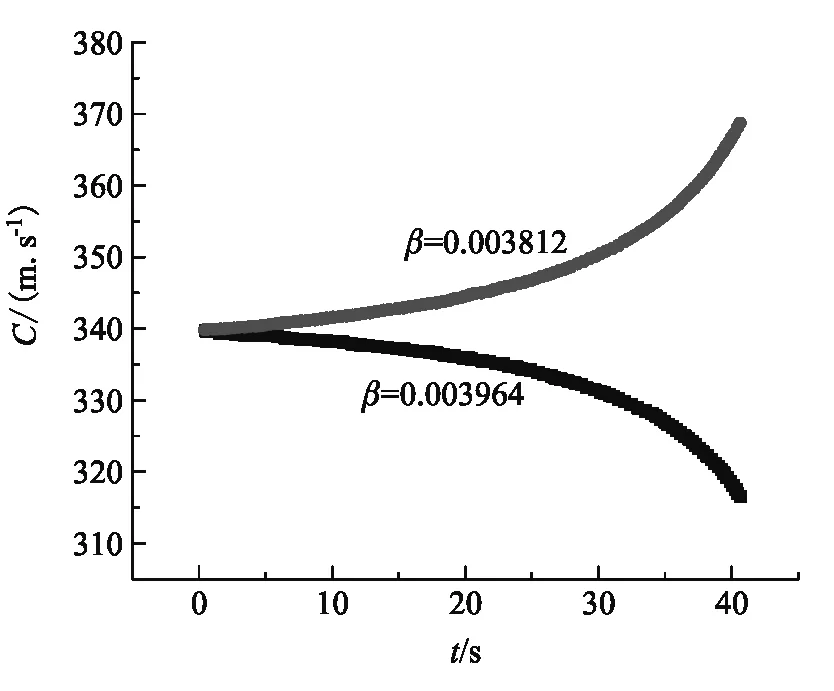
图8 β值的微小变化给声速计算值带来的影响.灰色点是β取值偏小的结果，黑色点是β取值偏大的结果

所以为了减小β的测量误差带来的影响，再考虑到这种影响随时间非线性增加的因素，在计算声速的时候应该截断时间较大的数据(也就是高频部分).怎样确定时间的截断点？从前面的分析来看，末端修正式(10)成立的条件是kr< 0.5，或者说是λ>4πr，对于基频来说就是4(L0-βt) > 4πr，因此要求：

(10)

将β和修正后的L0代入式(4)，应用式(10)截断高频部分的数据点，即可计算出声速测量的实验结果.

3.3 实验结果及其讨论

为了验证本实验方法的有效性，本文选择了一些不同的容器进行实验，它们的区别主要是长度和直径的比值不同.所得结果如表1所示.

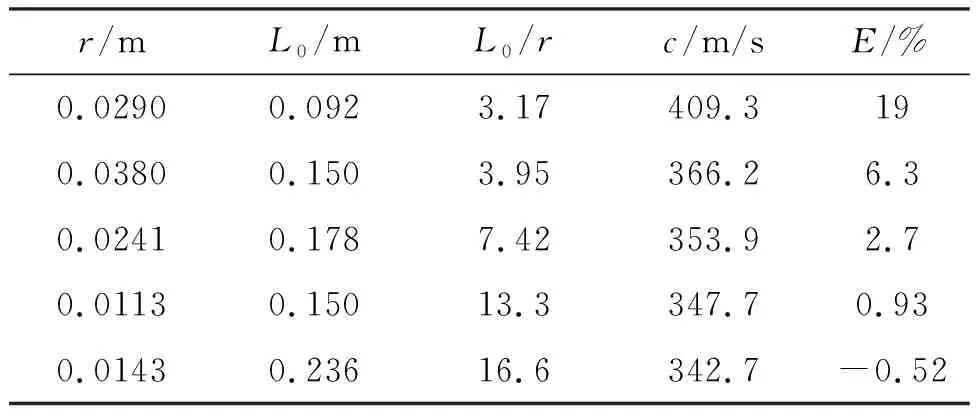
表1 不同长度与口径的圆形容器测得的声速

表1中r为容器内半径，L0为初始长度，L0/r为长度/半径比，c为按前述方法测量并计算所得的声速，E为与标准声速的偏差(实验时标准声速为344.5 m/s).从表中数据可以看出，细长容器所得结果更为准确，而且比值L0/r越大结果越好.当长度/半径比小于4的时候，误差较大，用这种方法来测量声速已不适用.

实际上，当长度/半径比很小的时候，容器已经不能看作是“管”了，而应该看做是一个“声容”，前述的讨论将不再适用.

4 结论

基于简易测量装置进行的空气柱共鸣实验，易于操作，但在物理原理的学习与理解方面还是很有价值的.在实验过程和数据处理过程中，学生能够在数学建模、数据发掘与提取等方面得到很好的训练，同时对如何改善实验环境、消除引起误差的因素等方面得到实际的锻炼，提高了实际动手解决问题的能力.

因为实验条件的限制，本实验研究的空气柱是在短而粗的容器中进行的，这就产生了一些新的问题.本文经过分析发现，在计算声速时需要考虑管口的声辐射导致的管口效应，应该给管长加上一个修正值，同时还需截断频率较高的数据点，这样才能得到正确的声速测量结果.作为基本声学知识的延伸，本实验方案提供的数据处理方法可以使学生在多方面得到训练和提高.