两连通气泡的平衡稳定性
盛天爽,余邱昱
(1. 南京大学 理科实验班,江苏 南京 210023;2. 南京大学 工科试验班,江苏 南京 210023)
气泡连通装置在许多热学问题中经常出现[1].如图1所示,在一根三通管的出气口A和B上涂上肥皂水,当向进气口吹气时两个出气口处分别会形成气泡A和B.在不考虑漏气情况下,初始形成的两个气泡的大小会随着时间的推移而发生改变,在一些特定的情况下,两气泡可以维持在一个平衡状态,但若有外界扰动,两气泡可能又会向另外一个平衡状态转化.

图1 气泡连通装置示意图
对气泡连通装置中气泡平衡稳定性的分析往往都是定性的,缺乏定量的计算.已有的少量文献[2,3]中给出了一些定量计算方法,但计算结果与实验结果仍有较大差异.本文在对气泡坐标加以方便定义的基础上,采用最小能量法准确实现了对气泡平衡稳定性的定量分析,数值计算的结果与实验测量的结果之间平均误差极小.
1 连通气泡平衡稳定性数学模型
1.1 气泡连通装置内部的能量分析
气泡连通装置是一种三通管结构,下面从4个方面考虑连通气泡变化过程中装置内能量的变化情况.1) 由于气泡内气压等于气泡外大气压和气泡表面张力附加压强之和,而附加压强远小于大气压强,因此可以近似设定连通气泡变化过程中管内气体压强不变.2) 考虑到不漏气情况下三通管内气体分子数不变,且外界压强和温度变化均可忽略,根据理想气体状态方程,此时气体体积不发生变化,即管内气体不对外做功.3) 若确保气体没有从外界吸热,则根据热力学第一定律,气体的内能不发生变化.4) 气泡膜有一定的重力势能,经过推算可以证明其数量级远小于表面张力能,故气泡的重力势能忽略不计.基于以上4点考虑,可以大胆假设气泡连通装置中能量的变化仅源自于气泡变大与缩小时表面张力能的改变,气体在管内的流动使得能量可以在两个气泡之间转移.因此,根据表面张力能方程,对连通气泡内的能量分析只需考虑两个气泡表面积的变化即可[4].
1.2 连通气泡平衡稳定性的最小能量法分析
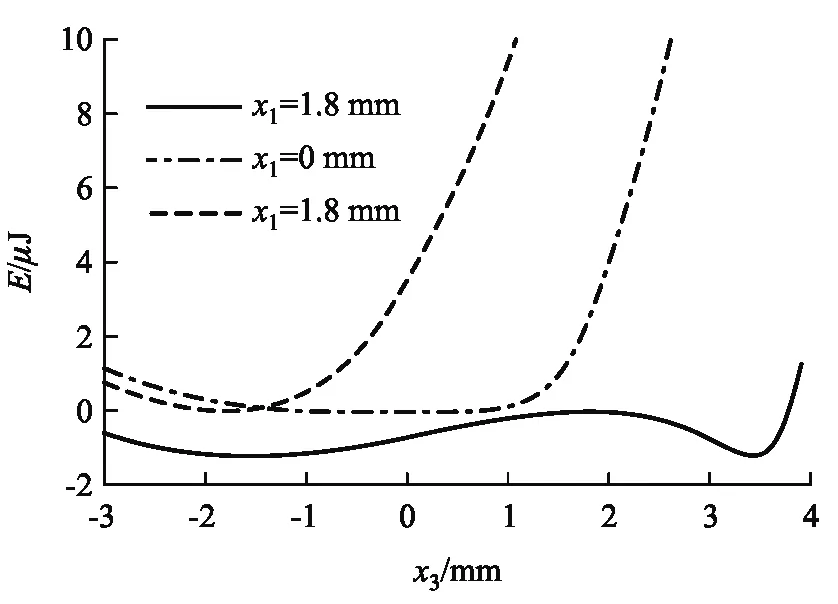
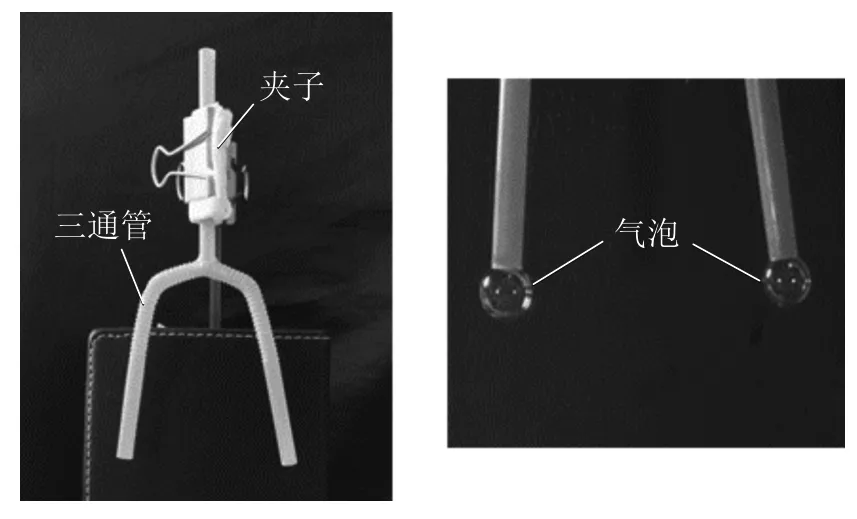
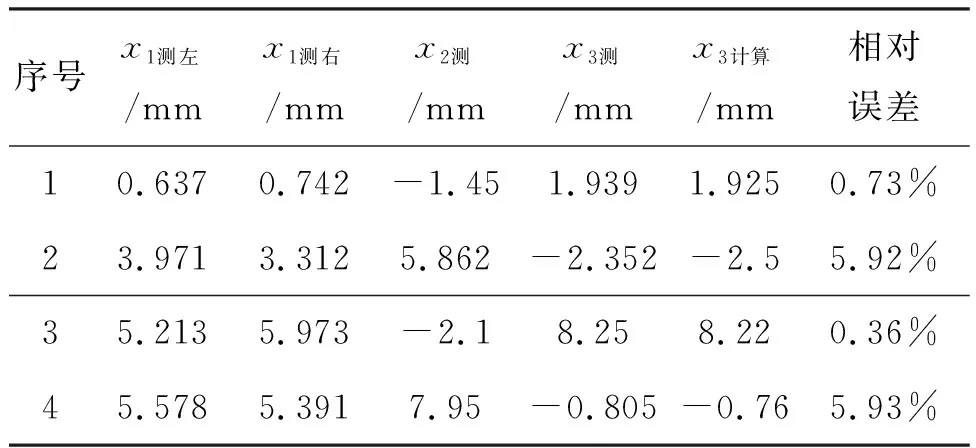
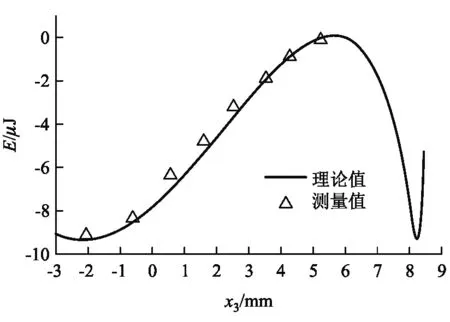
为了便于分析,首先定义‘气泡坐标’.假设三通管管口半径为r,取管口下方r处为原点,方向垂直向下,建立x轴坐标系,如图2所示.将气泡顶点处的坐标定义为气泡坐标,并明确气泡坐标x>0时为大于半球状态,气泡坐标-r 图2 大于半球和小于半球气泡坐标示意图 无论气泡形状是大于半球还是小于半球,均可由勾股定理得到用hi和r表示的气泡半径Ri, (1) 则根据球冠表面积和体积公式可以很容易推导出气泡的表面积和体积分别为 (2) (3) 为了不失一般性,假设左右两个气泡初始等大且气泡坐标为x1,则相应的气泡半径和气泡高度记为R1和h1.当发生扰动后,连通气泡形态发生变化,记左边管口的气泡坐标为x2,相应的气泡半径和气泡高度为R2和h2;右边管口的气泡坐标为x3,相应的气泡半径和气泡高度为R3和h3; 规定气泡坐标为0时气泡的表面张力能为0.则根据表面张力能公式,连通气泡的能量E可由下式给出,其中α为表面张力系数. (4) 同时,由于封闭管内气体的体积恒定,因此左右两个气泡的气泡坐标满足式(5)所示的体积约束条件. (x2+r)[3r2+(x2+r)2]+(x3+r)[3r2+(x3+r)2]= 2(x1+r)[3r2+(x1+r)2] (5) 显然,式(5)是关于x2和x3的非线性方程.根据式(1)—(3),理论上可以用x3表示x2,然后代入能量公式(4),将能量E表示为参数x3的函数.再根据最小能量法的基本原理,首先计算出能量E的一阶导数为零的点,此即为连通气泡的平衡点.进而再计算出在平衡点处能量E的二阶导数,如果E的二阶导数大于零,则为稳定的平衡点,如果E的二阶导数小于零,则为不稳定的平衡点.需要指出的是,利用拉格朗日乘子法,使用式(5)和(4)构造拉格朗日函数也可以求出该平衡点的坐标. 气泡能够真实存在,则要求连通气泡必须平衡且稳定.首先,假设气泡膜的厚度各处均匀,且不考虑蒸发,则气泡膜厚度随着气泡增大而减小,当厚度小于极小值时,气泡膜就会破裂.其次,三通管左右出气口的气泡坐标均不得小于管口坐标,否则气泡就不再存在.根据这2个约束条件,可以给出气泡坐标的范围. 而在实际情况中,由于三通管管口直径较小,肥皂液足量,当气泡较小时,第一个约束条件总能够满足.因此最终的约束条件可以减少为以下两个不等式:x2>-r,x3>-r. 由于计算量大,因此无法通过解析方法进行稳定性分析.本文通过编写Mathematica程序进行数值计算,绘制出气泡能量变化曲线图,进而准确判定连通气泡的平衡稳定性.相应的实验表明数值计算结果与实验结果吻合良好. 选定三通管半径r=3mm,分别给定以下3种典型状态的初始气泡坐标:x1=1.8mm,x1=0mm和x1=-1.8mm.将这3种初始的气泡坐标分别代入能量方程,绘制系统能量E随管口气泡坐标x3的变化曲线,如图3所示. 从图3可以看出,当初始气泡坐标x1=-1.8mm时,气泡为小于半球状态,能量曲线在初始点处有极小值E=1.86×10-22J,表明初始情况即为连通气泡的稳定平衡点.当初始气泡坐标x1=0mm时,气泡为等于半球状态,这时能量曲线在初始点附近处处为0,满足随遇平衡条件.当初始气泡坐标x1=1.8mm时,气泡为大于半球状态,此时能量曲线在初始点处有极大值E=1.5×10-21J,表明气泡此时处于不稳定平衡状态,稍有微扰就会偏离平衡点. 同时,在该能量曲线极大值点的左右两侧,分别存在一个极小值点.左侧为x3=-1.6mm,E=-1.2×10-6J;右侧为x3=3.4mm,E=-1.2×10-6J.通过计算可知这两个极小值点恰好各自对应着一种特殊的稳定平衡形态,即左右两个气泡的形状合起来恰好为一整球. 图3 3种典型初始状态气泡能量变化曲线 以上对3条能量曲线的定量分析结果与文献[1]的定性分析结果完全一致,表明了使用最小能量法分析气泡连通装置平衡稳定性的有效性. 利用市售一次性吸管(管口直径为6mm)和杂货店中买到的儿童肥皂水(测得室温下的表面张力系数为0.036N/m),制成一个简易的气泡连通实验装置,如图4所示.先在三通管的两个下端出气口涂抹肥皂水,然后从上端进气口口向管内鼓气,直至在下端口获得两个完整的气泡,最后用夹子夹住上端口.为了提高实验准确性,可以用一次性针管将气泡内残存的少量肥皂液吸走,也可以用针管向两气泡内充气或吸气,对气泡形状进行微调,以满足实验要求.利用该简易装置,设置不同的初始气泡坐标进行多次实验.实验中通过对气泡拍摄照片,测量照片上的像素个数进而换算成长度的方法分别获得两个气泡的气泡坐标.实验发现,当两个初始气泡小于半球时,气泡非常容易破裂,而气泡等于半球的情况也不易达到,因此本实验仅针对两个初始气泡均为大于半球状态的情况进行扰动测量,最终稳定时的测量结果与数值计算结果对比如表1所示. 图4 气泡连通实验装置 表1 气泡连通装置稳定性分析的测量值与计算值对比 实验进行了4组,其中x1测左和x1测右分别表示初始时左右两个气泡的坐标,通过微调尽量使两者接近.将两个初始气泡坐标分别代入式(3),计算出两气泡体积之和再除以2,得到平均气泡体积,再利用式(3)解出平均气泡坐标.数值计算时取平均气泡坐标为初始气泡坐标x1.另外,x2测和x3测分别表示系统稳定时测定的左右气泡坐标,x3计算表示通过数值计算得到的右侧气泡坐标.从表1可以看出,实验结果与数值计算结果吻合良好,相对误差优于文献3给出的比对结果. 此外,在第3组实验中,还利用Tracker软件对左右两个气泡进行了追踪拍摄,获得气泡坐标x2与x3的8组数据.通过表面张力能公式分别计算出这8种状态下连通气泡内的能量,绘制成气泡能量曲线,与使用最小能量法获得的数值计算结果相比较,如图5所示. 图5可以看出,通过实验得到的测量值与通过数值计算得到的理论值基本吻合.在气泡坐标x3小于3mm时,实验测量值与理论值略微产生偏差,且实验测量值比理论值偏大.分析认为这是由于当气泡缩小时,会有少量肥皂液聚集在气泡顶部,从而导致气泡形状发生改变,气泡不再是完美的球冠,因此造成一定程度的偏差. 图5 连通气泡能量曲线的实验与计算对比 1) 对连通气泡中的能量变化进行分析,判定通常情况下气泡连通装置中能量的变化仅源自于气泡变大与缩小时表面张力能的改变.2) 定义气泡坐标概念,明确3种典型的气泡状态,并且规定等于半球状态时气泡的表面张力能为零.3) 通过对气泡表面张力能的分析,利用最小能量法,计算连通气泡的稳定平衡点和不稳定平衡点,从而对气泡连通装置的平衡稳定性做出定量分析.4) 通过实验,对不同初始大小的气泡进行扰动跟踪,测量得的气泡最终稳定点与数值计算得到的理论值吻合度较高,实验与理论分析所获得的连通气泡能量变化曲线也基本吻合,从而进一步验证了使用最小能量法分析气泡连通装置平衡稳定性的有效性和准确性.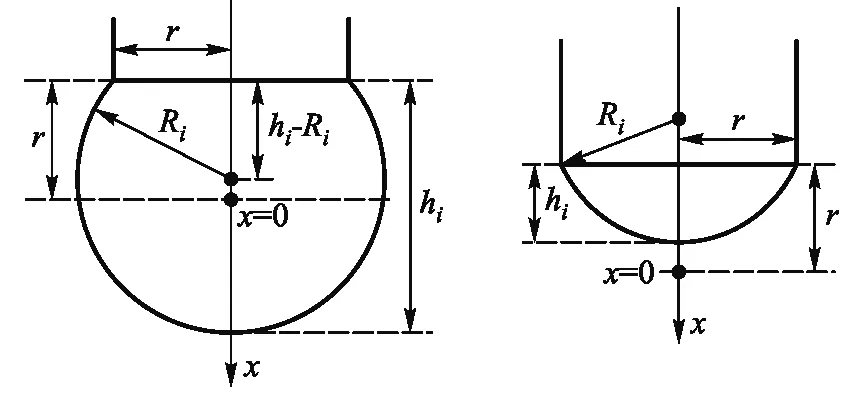
1.3 满足气泡成形的约束条件
2 连通气泡平衡稳定性的数值计算与实验
2.1 数值计算
2.2 实验验证
3 总结

