弹簧摆动力学行为演示仪

何玉吉, 汪金芝，梁卓凡，李青峰

( 宁波工程学院 机器人学院, 浙江 宁波 315211 )

实际情形中的力学系统往往都是非线性的.而在解决问题时，为简化计算，常将其近似为线性系统，在如弹簧振子、单摆等振动系统中，非线性项的影响可忽略，线性化近似处理后获取的结果还是较为理想的.而对于弹簧摆系统，如果没有依据地去掉非线性项将引起无法解释的误差甚至是本质性的偏差和错误.对这类非线性系统的研究能有效揭示经典力学的复杂和变化的一面[1].

近些年，非线性振动系统的研究获得许多成果，在电子学以及航空航天等领域广泛应用，其中混沌理论为解决非线性保守系统提供了可能.在以人工智能方向为代表的新工科教育改革的背景下，将非线性振动系统加入大学物理知识体系内具有重要的意义[2].而弹簧摆结构简单，适合在教学中推广应用，笔者运用拉格朗日方程对该典型的非线性系统——弹簧摆系统进行了理论分析，并借鉴了频闪法的思想，设计实验装置，采用图像处理技术开发了该系统运动轨迹的采集和模拟软件，将弹簧摆系统混沌行为进行可视化.

1 实验原理

弹簧摆系统由轻质弹簧和小球组成，如图1所示.弹簧的劲度系数为k=0.95 N/m，弹簧的原长为l=0.2 m，重物到悬挂点之间的距离为r，与竖直方向夹角为θ，重物质量m=0.02 kg且看成质点.短时间内弹簧摆二维运动的能量损失可忽略不计，因而将系统进行理想化处理，近似为保守系统.

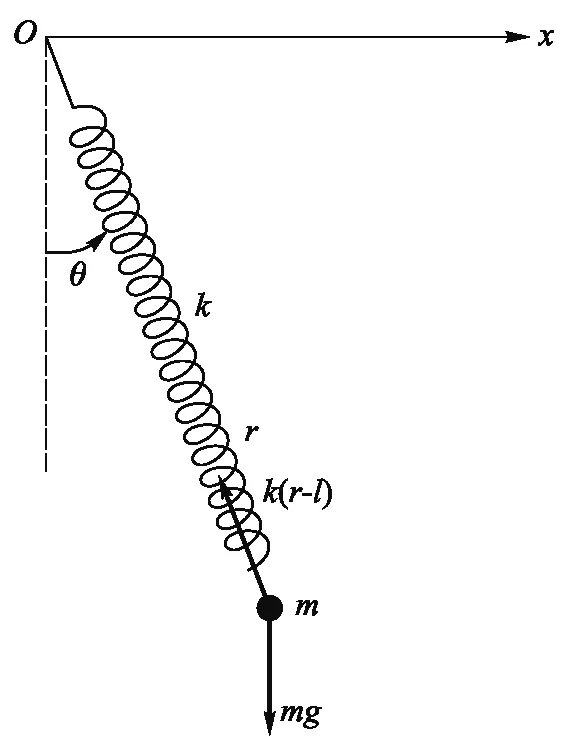
图1 弹簧摆系统示意图

如图1建立弹簧摆模型，以悬挂点为坐标原点，沿水平方向为x轴，竖直方向为y轴建立直角坐标系，系统的自由度为2，分别取弹簧原长位置与坐标原点为弹性势能和重力势能的零点[3].

广义坐标下系统任意时刻的动能为

(1)

其势能为

(2)

系统的拉格朗日函数为[4]

(3)

由于该系统为保守系统，则广义力Qj=0，可解得该系统的运动方程[5]为

(4)

当θ或r固定时，在小角度情况下(sinθ≈θ)，得到式(5)，可将系统运动近似为弹簧振子和单摆运动的组合：

(5)

通过MATLAB和Mathematica对系统进行模拟分析，制出弹簧摆的轨迹图、相图及时序如图2所示[6].从图2 (a)轨迹图中可看出，重物在二维平面内作非周期运动，但运动轨迹具有高度对称性.从相图 图2(b)、(c)和时序图 图2(d)、(e)可得，弹簧摆在径向和切向作周期运动，与理论分析相一致.

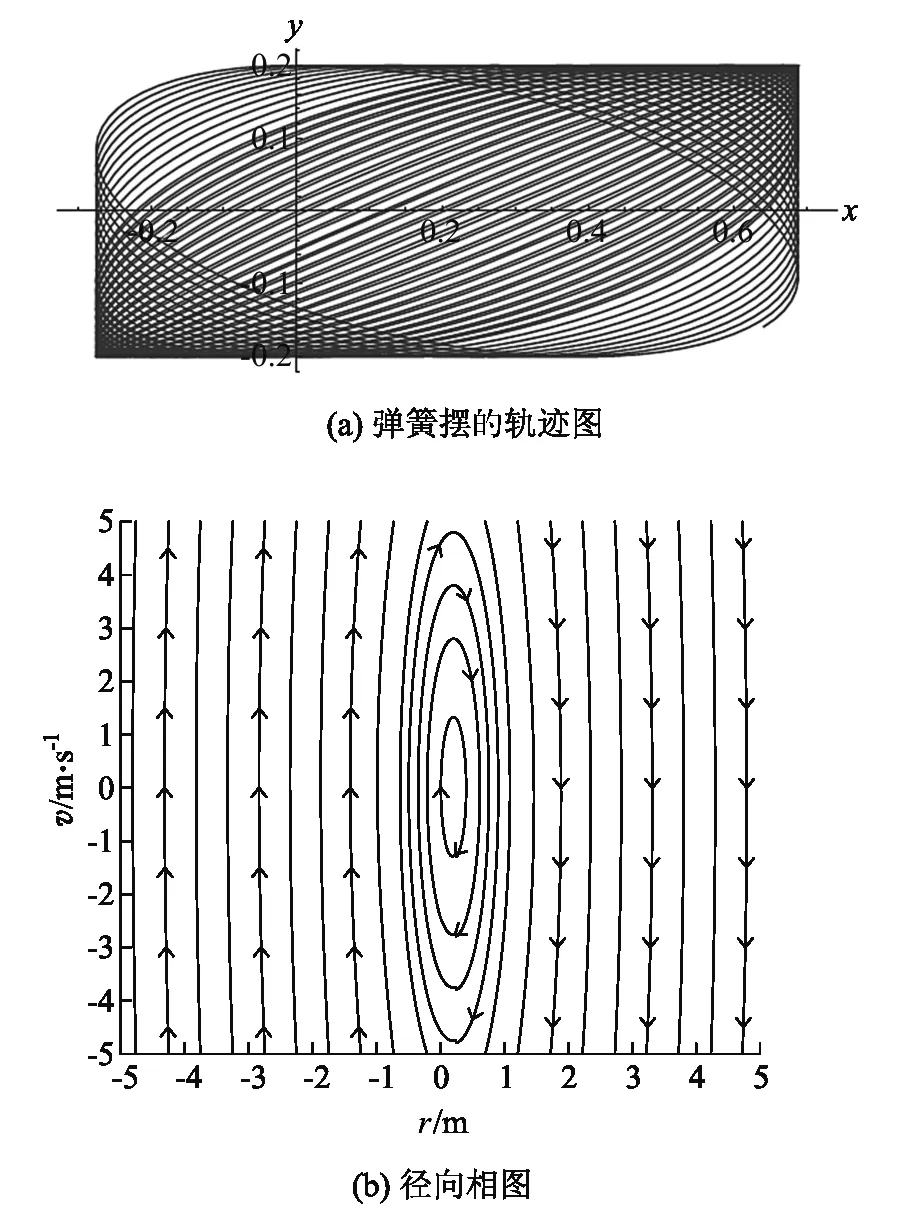
图2 弹簧摆轨迹图、相图和时序图

2 实验装置

弹簧摆演示仪的结构如图3和图4所示，上板开槽，弹簧和经涂色处理的重物如图悬挂，装置后设置有黑布筒，实验时拉下黑布保证背景单一，提高图像识别准确率.装置左侧设有释放装置，其长度和高度可调，经合理调整后使用可很大程度上减少第三维度的系统能量损失，减小实验误差；右侧为数显卡尺.USB摄像头架放置于装置的正对面.当将重物拉至释放装置凹槽处，静止释放后，系统做弹簧摆运动，USB摄像头实时拍摄的同时，将数据传入电脑的图像处理软件进行分析和处理[7].

图3 实验装置实物图

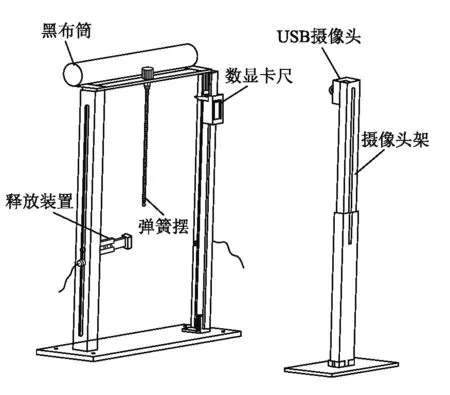
图4 装置示意图

基于HSV色彩空间下的目标检测与跟踪[8]，编写了针对该实验的配套图像处理软件.系统识别目标为绿色和红色物体，其中绿色为基准点，固定于弹簧悬挂点处，重物涂成红色，作为运动点.

具体图像处理操作为：对检测目标进行阈值处理计算得到像素值范围，USB摄像头以30帧/s读取图像，将每张图片中所有在像素值范围内的像素点转移到掩膜上，并对掩膜上的图像进行膨胀操作，使之前被消去部分得以部分填充回来，本软件中的形态学操作内核为矩形.最后获取处理后矩形的几何中心，作为目标点坐标并输出.

为方便观察实验结果，存储的坐标点数据在软件内进行可视化处理，实时追踪并绘制弹簧摆轨迹图与时间序列图(图7)，软件原理与界面如图5和图6所示.

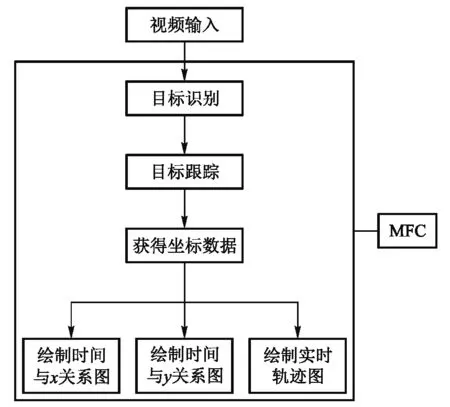
图5 软件原理

图6 软件界面

3 实验内容和步骤

1) 旋转调平螺丝，调整装置水平.

2) 调整释放装置位置，保证弹簧摆在二维平面运动.

3) 将摄像头连接电脑并调整位置，使顶部定位的绿色方块和红色砝码均在画面中.

4) 点击打开摄像头并点击“开始跟踪”.

5) 将重物拉至释放装置的位置，无初速度释放，使其开始做弹簧摆运动.

6) 点击“开始记录”对弹簧摆运动情况进行读取和处理，一段时间后停止记录.

7) 再点击“X-T图”和“Y-T图”绘制x和y方向时间序列图.

8) 点击“打印坐标点”，用MATLAB处理打印出的坐标数据并分析其运动.

图像处理软件最终绘制的弹簧摆轨迹和时间序列如图7所示，可以看出，实验结果与理论结果图2 (a) (d) (e)具有一致性，达到了较好的实验和演示效果.经重复实验，10～20 s左右弹簧摆系统能量损失可忽略不计，轨迹图效果较好，具有较好的理论与实验对比研究价值.

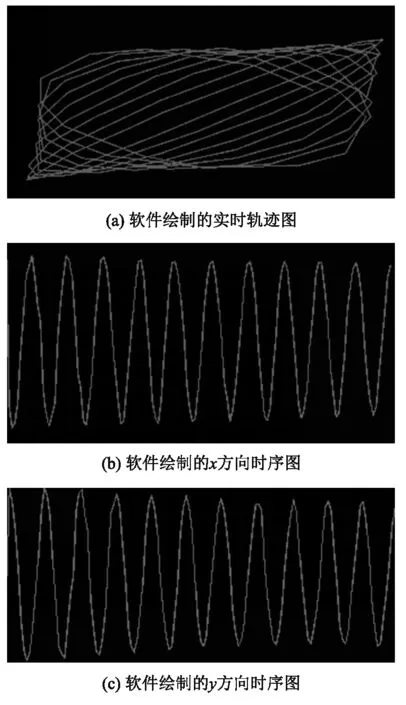
图7 实验结果

5 结论

本文介绍了非线性保守的弹簧摆系统的原理及演示实验，该系统结构简单，实验操作便捷，获得的实验结果较为理想与直观，是非线性系统教学的典型例子，涉及的知识点易被学生接受，适合用于本科物理教学.可弥补现有教学中非线性系统只能进行线上模拟仿真的不足，能激发学生的兴趣.