含内阻的拉杆组合转子双稳态振动特性
王龙凯 王艾伦 金 淼 尹伊君
1.中南大学轻合金研究院,长沙,410083
2.中南大学高性能复杂制造国家重点实验室,长沙,410083
0 引言
拉杆组合转子结构在航空、电力、船舶等行业中得到了广泛的应用,它的各级轮盘通过拉杆螺栓预紧后连接为一体,这种特殊结构形式的转子不再是一个连续的整体[1]。这类型转子的工作转速较高,常在一阶或二阶临界转速之上运转。高转速运行工况以及组合转子轴承系统的内在非线性,使转子在某些工况或外界扰动下不再做定常运动,某些转速区域可能会出现振幅忽大忽小的跳跃现象,即双稳态振动现象。当转子做非同步涡动时,轮盘的内阻参数会显著影响转子的振动响应[2]。因此,研究高速拉杆组合转子非线性双稳态振动特性并掌握内阻作用机理,对保障机组长期安全稳定运行具有非常重要的意义。
在高速转子非线性动力学方面,国内外学者做了大量的研究工作。宾光富等[3]采用频谱分析法研究了高速转子的振动特性,VARNEY等[4]分析了转静碰摩转子的分岔特性,NEMBHARD等[5]通过实验揭示了多故障转子轨迹的演变规律,KHANLO等[6]研究了碰摩转子的横向-扭转耦合振动。在组合转子动力学研究方面,WANG等[7]研究了裂纹拉杆转子稳定性;HU等[8]将轮盘接触层等效为抗弯弹簧,研究了拉杆转子的碰摩特性;黑棣等[9]采用长轴承理论求解油膜力,研究了拉杆转子非线性动力学行为;何谦等[10]、殷杰等[11]采用有限元法计算了接触界面的法向刚度;于平超等[12]将轴承反力简化为三次函数,研究了航空发动机转子振动特性;李辉光等[13]考虑了拉杆附加刚度,采用floquet理论研究了拉杆转子稳定性;程礼等[14]发现某型发动机在某扰动下会出现振动突跳现象,他将转子简化为典型的拉杆组合转子结构,将轴承刚度设为定值,采用谐波平衡法研究了双稳态振动特性。现有文献主要关注碰摩、裂纹、接触刚度对转子振动特性的影响,关于转子双稳态振动特性方面的研究较少,且都没有考虑内阻效应,因此,亟需研究并掌握内阻对组合转子双稳态振动特性的影响规律。
本文根据拉杆组合转子结构和力学特点,构建含轮盘接触、油膜以及内阻的组合转子非线性动力学模型,采用时频分析法研究拉杆组合转子系统非线性双稳态特性及内阻效应。
1 含内阻的组合转子动力学建模
组合转子按拉杆类型可以分为周向拉杆组合转子和中心拉杆组合转子。周向拉杆转子轮盘间的结合面为平面,通过摩擦力来传递盘间载荷,而中心拉杆转子通常采用端齿结构来传递盘间载荷。轴承特性和界面接触非连续性使得组合转子的振动特性非常复杂,在某些工况下会出现双稳态振动、涡动振幅跳跃等现象。周向拉杆组合转子制造难度和成本较低,应用更为广泛,因此,本文以图1所示轮盘间环形平面接触的周向拉杆转子为例,探究含内阻的拉杆组合转子非线性动力学行为。图1中,N1、N2、N3、N4分别为1号轴承、1号盘、2号盘和2号轴承的集中质量点;Fub1、Fub2分别为作用在1号盘和2号盘上的不平衡力;ks为转轴刚度。
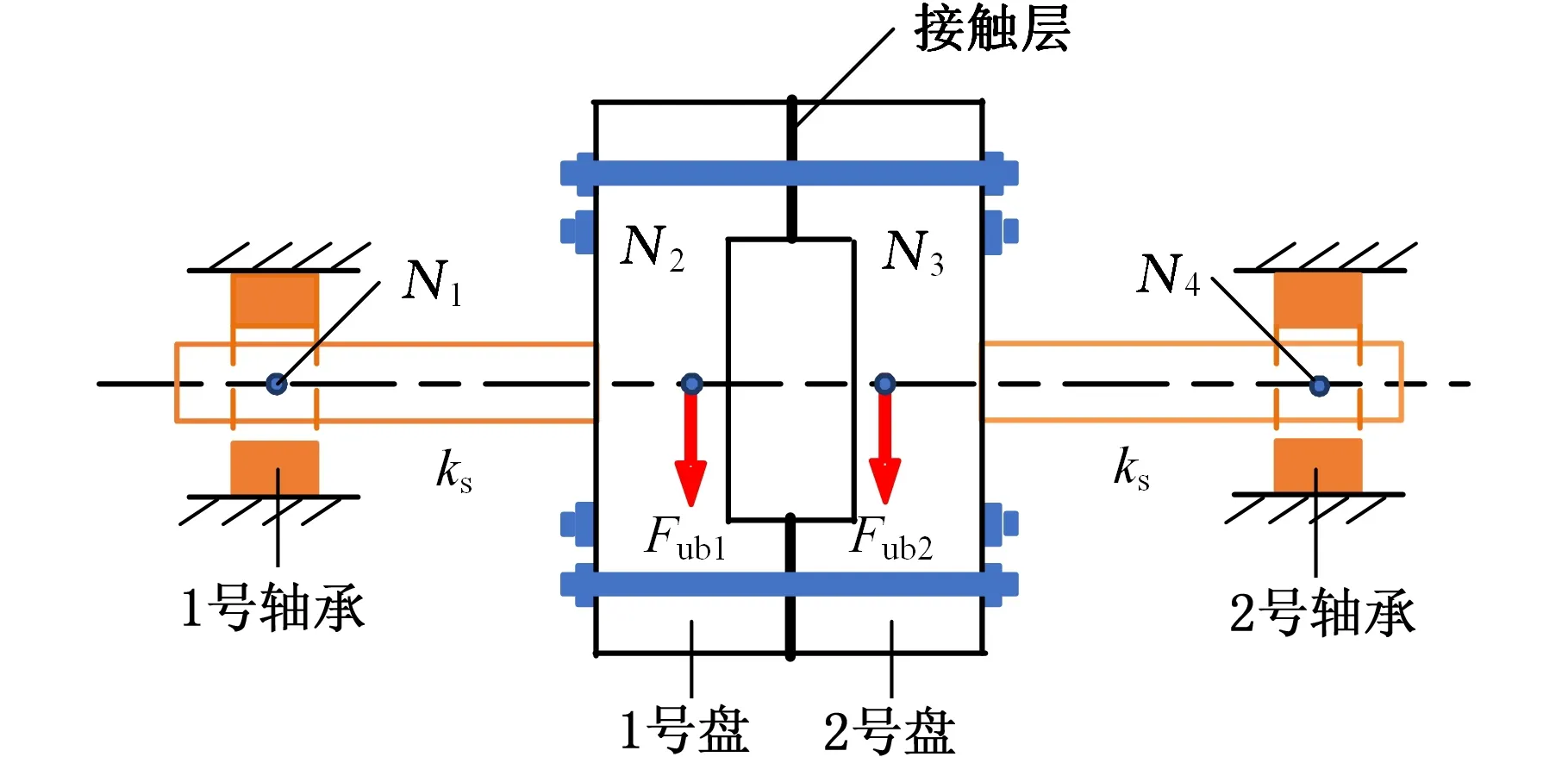
图1 转子结构示意图
1.1 轮盘接触刚度计算
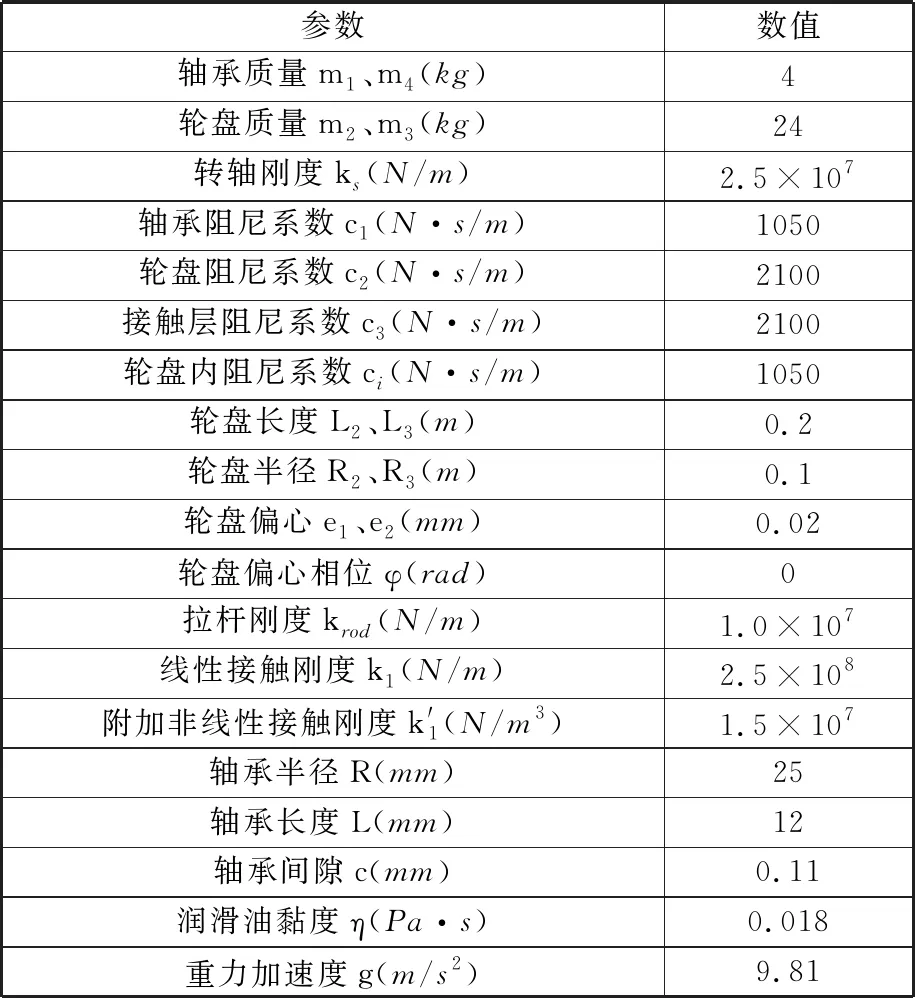
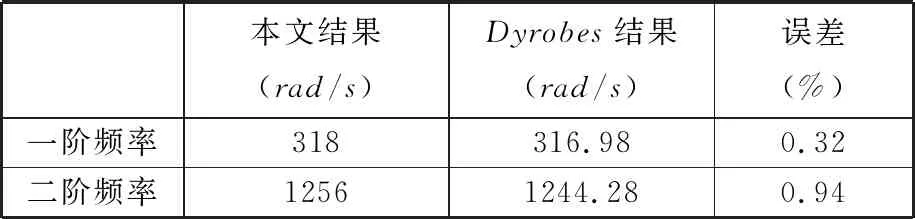
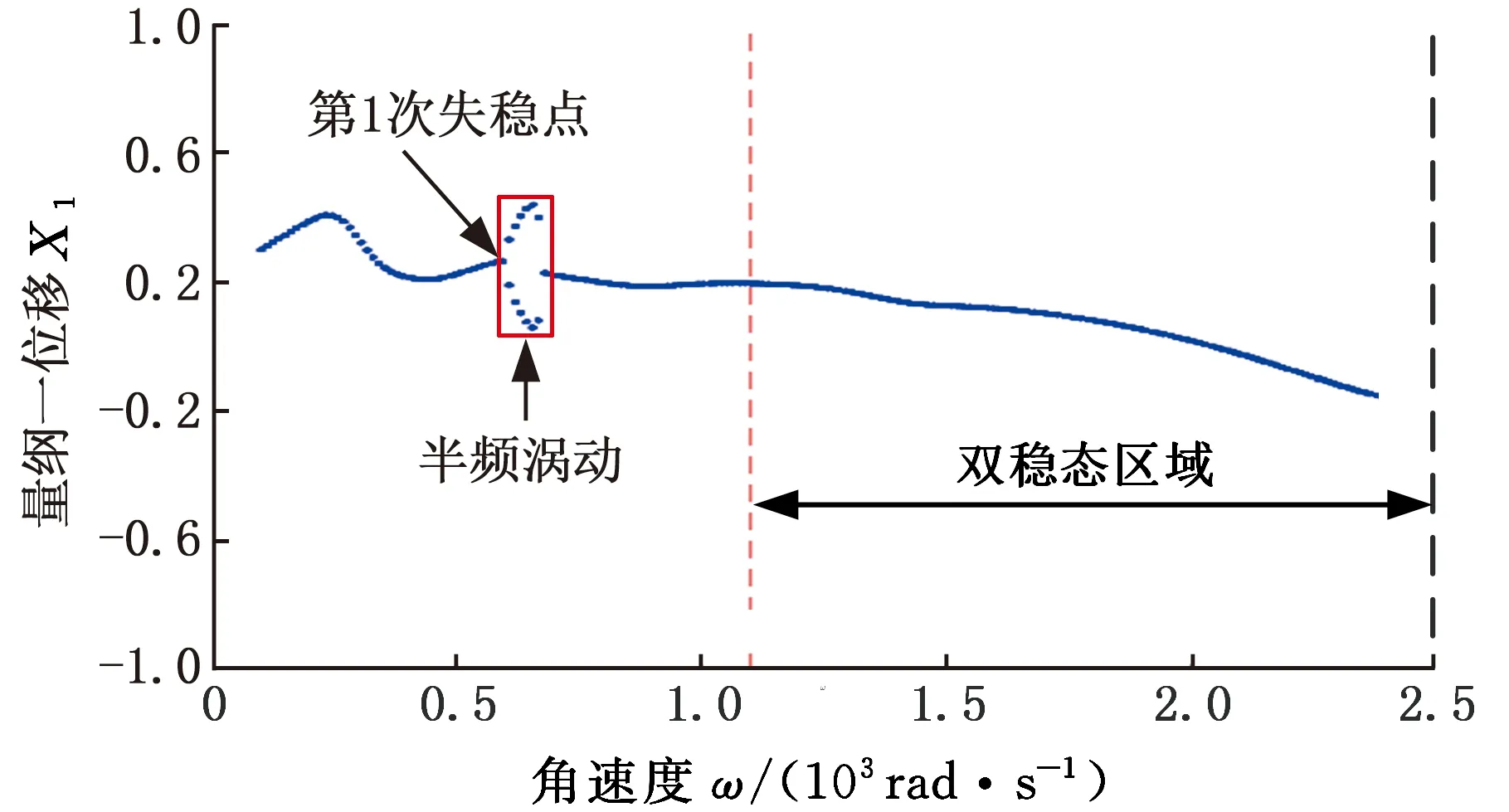
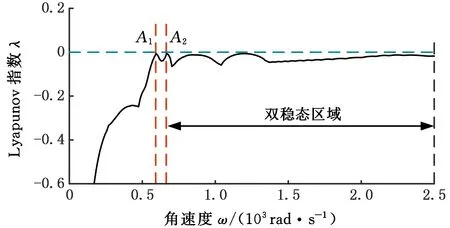
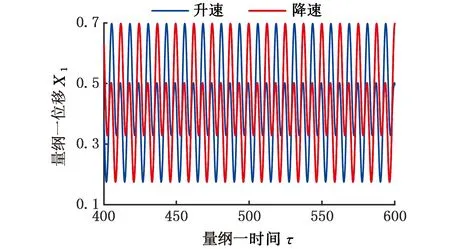
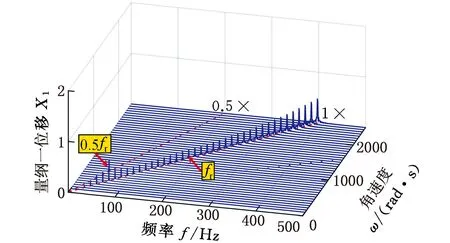
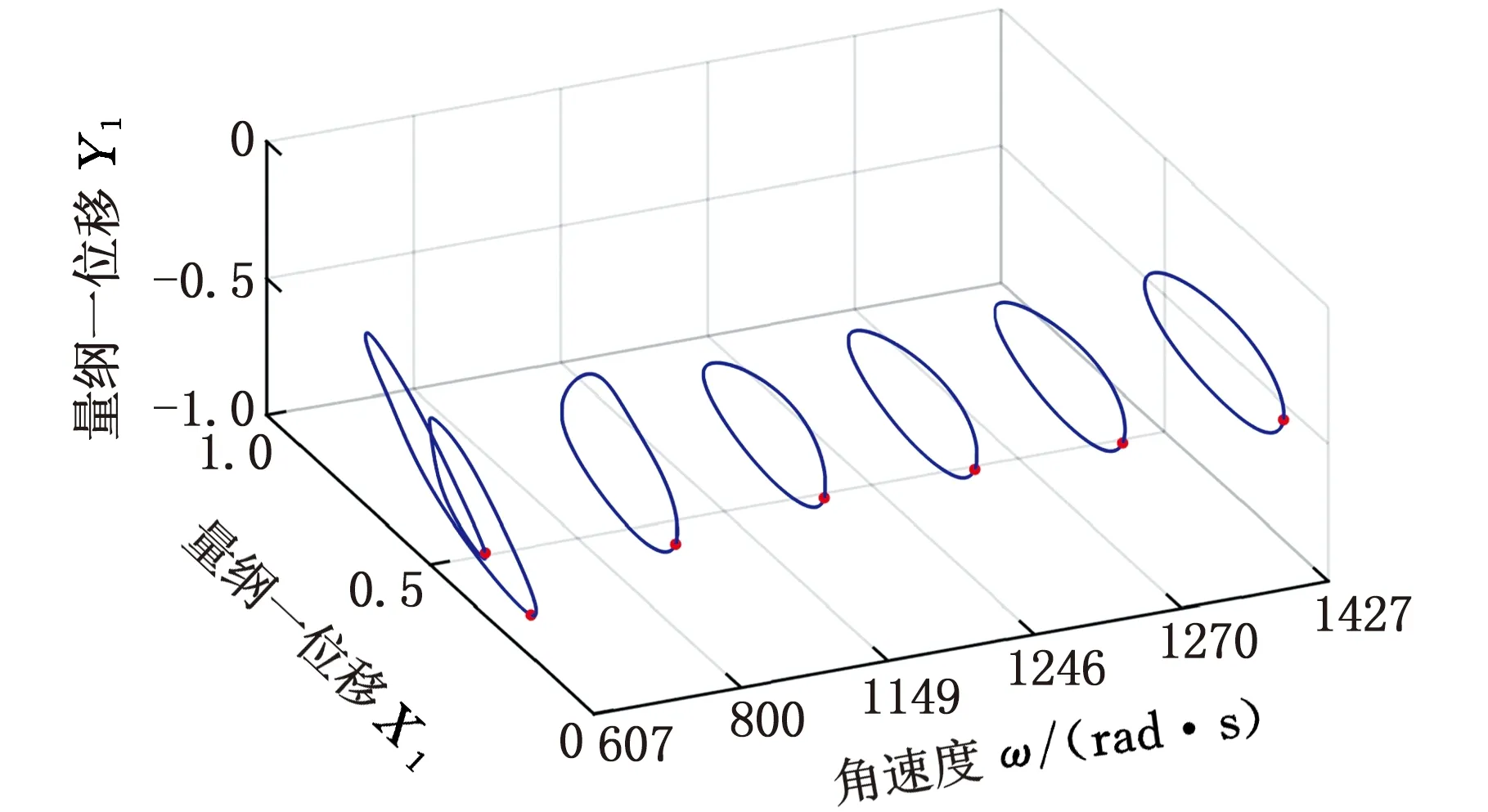
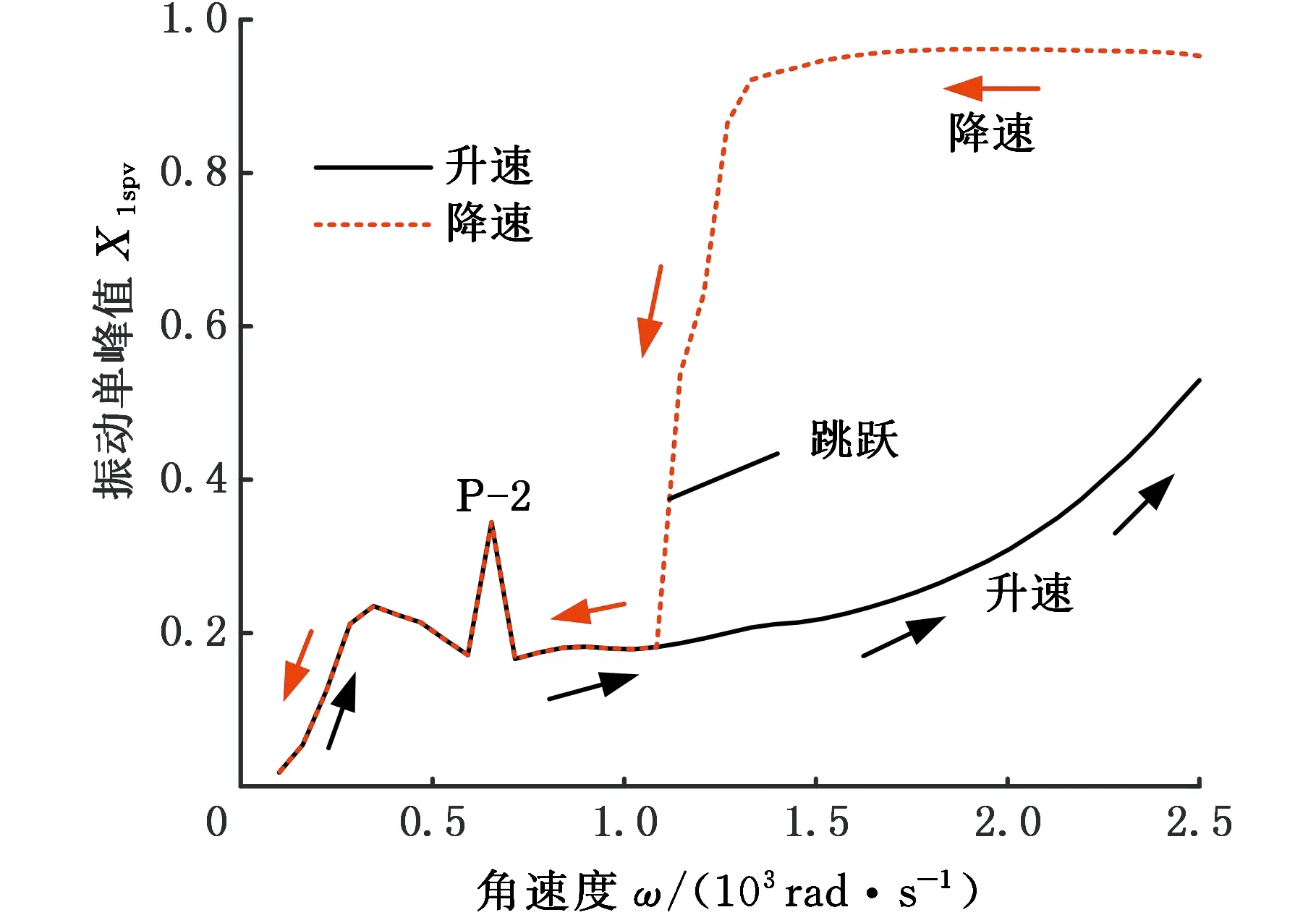
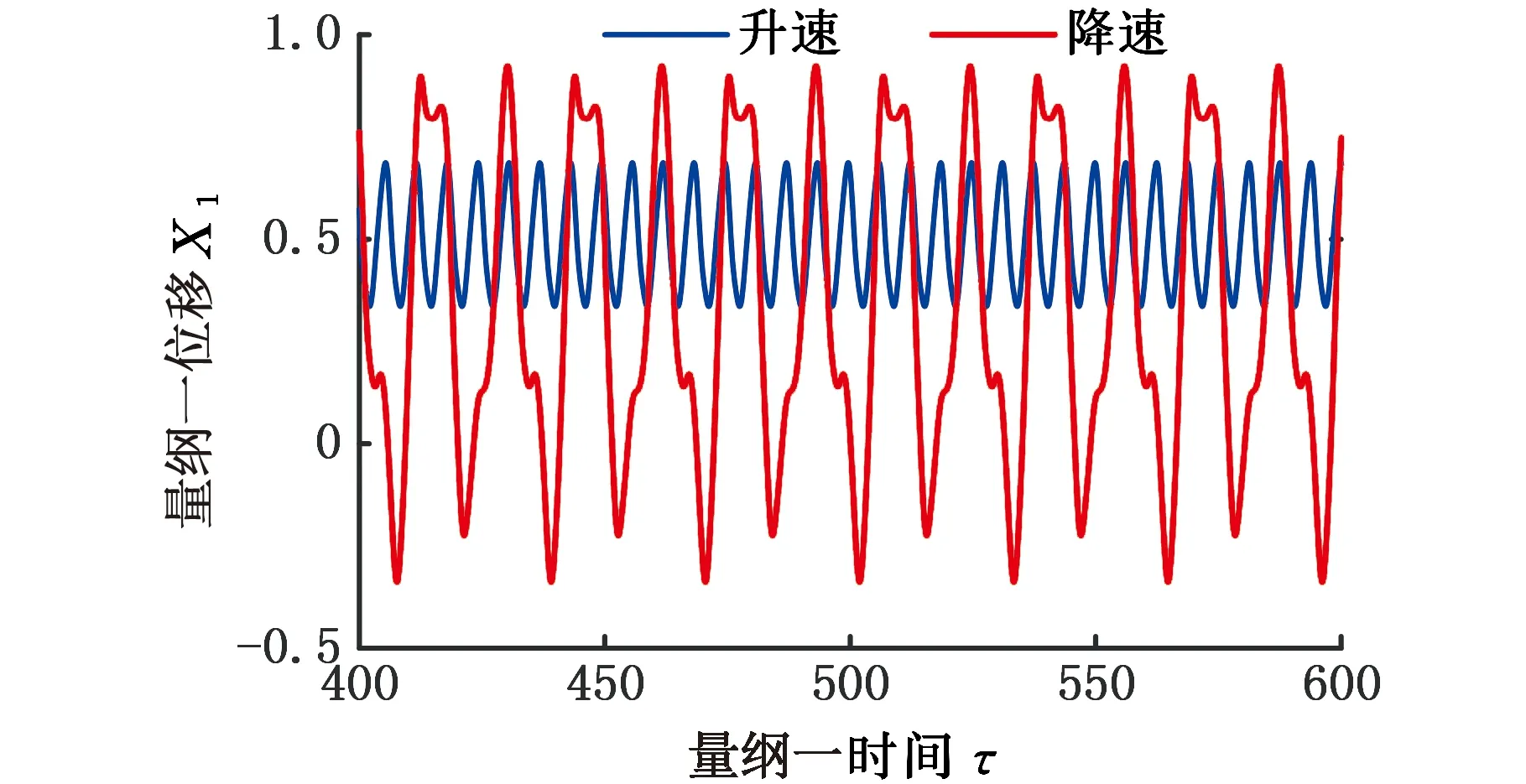
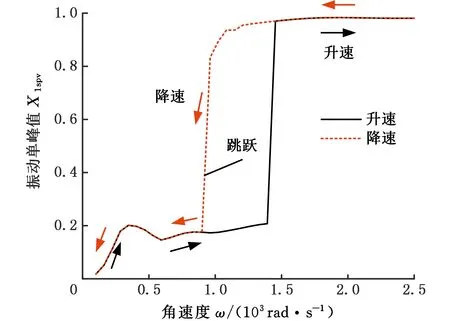
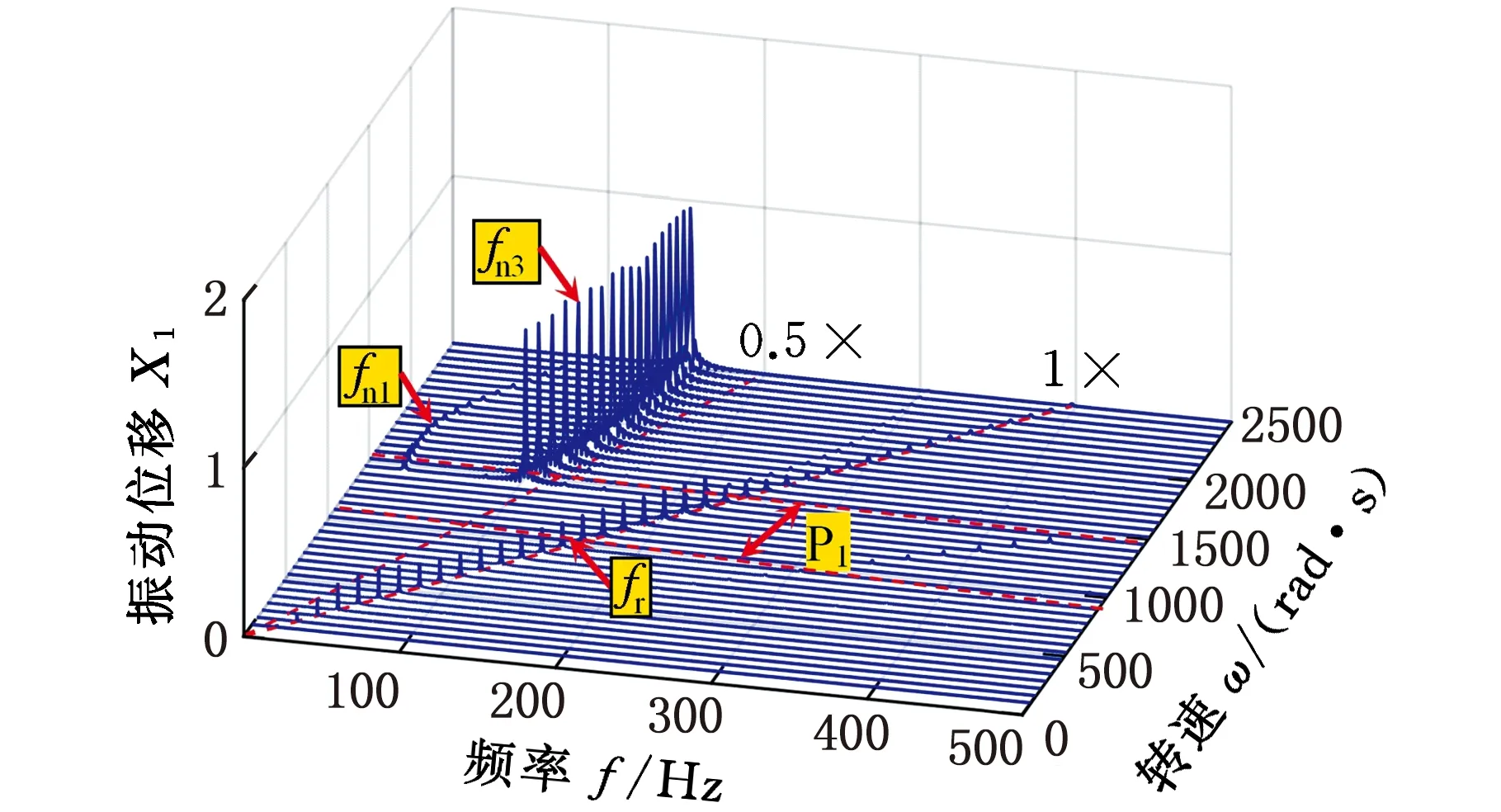
轮盘通过均布拉杆压紧为一整体,具有典型的非连续特性,如图2所示,d为杆直径,D为匹配孔直径,且有d 图2 拉杆转子接触界面 以OXZ平面为例,定义轮盘间X方向的相对位移为Δx,半径差ε=(D-d)/2。拉杆与其匹配孔之间存在间隙,横向振动中,当轮盘间的相对位移较小(|Δx|<ε)时,拉杆与匹配孔不发生接触[8],拉杆预紧力作用下的轮盘间接触层的抗弯刚度为k1(可由微元体方法[13]求得)。当轮盘间的相对位移大于半径差时,拉杆与其匹配孔发生接触,系统将产生拉杆附加抗弯刚度k2。用三次幂函数y=k′1(Δx)3拟合非线性恢复力 可得图3所示的附加非线性恢复力曲线,其中,k′1为非线性刚度。 1.分段线性恢复力 2.三次幂函数模型 综上,结合线性刚度k1和非线性恢复力Fcx,可推导出轮盘接触层之间的非线性恢复力: (1) 由式(1)可知,轮盘间接触只有达到一定条件时才表现出明显的非线性特性,而此条件取决于转子-轴承系统整体的动力学特性。 拉杆转子结构复杂,且两端采用滑动轴承支撑,这使得组合转子涡动形式复杂且具有多样性。在非同步振动情况下,内阻势必会对转子非线性动力学特性产生显著影响,因此,在研究组合转子非线性动力学行为时,需考虑轮盘内阻效应。材料的内阻尼力与轮盘相对于旋转轴的速度成正比,内阻力在旋转坐标系(转动角速度为ω)下可表示为 (2) 式中,ci为轮盘材料内阻尼,下标i表示内阻。 使用坐标变换公式[2]可推导出内阻力在固定坐标系下的表达式: (3) (4) 式中,Fcx1、Fcy1分别为作用在1号盘上的非线性恢复力在X方向和Y方向的分量;Fcx2、Fcy2分别为作用在2号盘上的非线性恢复力在X方向和Y方向的分量;m1、m2、m3、m4分别为1号轴承、1号盘、2号盘和2号轴承的等效集中质量;c1、c2、c3分别为轴承自阻尼系数、轮盘外阻尼系数和接触界面阻尼系数;e1、e2分别为1号盘和2号盘的质量偏心距;φ1、φ2分别为1号盘和2号盘的偏心相位角;s为Sommerfeld数,s=ηωRL3/(4c2);η为润滑油黏度;R为轴承半径;L为轴承长度;g为重力加速度;c为轴承间隙;Fx、Fy分别为X和Y方向的轴承量纲一非线性油膜力。 该拉杆转子采用滑动轴承支撑,假定润滑油为等温、不可压缩的层流,由于长径比L/D<0.25,故本文采用基于短轴承假设的Capone油膜力模型[15],其量纲一非线性油膜力可表示为 (5) 对转子各组件进行模化处理后[2],为进行临界转速分析,将运动方程中的阻尼力、质量偏心引起的不平衡力和附加非线性恢复力假定为0;采用直接刚度系数计算线性轴承力,并求解运动方程的特征值,得到转子的前二阶临界转速分别为318 rad/s和1256 rad/s。为验证模型计算的正确性,根据转子结构参数(表1),采用基于有限元分析的Dyrobes软件构建组合转子动力学模型。建模过程中,将连接轴段1-2和3-4模化为无质量弹性轴段;各节点处质量采用刚性轮盘模化;轮盘连接段2-3采用虚拟轴段进行处理。Dyrobes的计算结果与本文所得结果如表2所示,两者的误差较小。 采用4阶Runge-Kutta法[2]对式(4)数值求解,采用分岔图、李雅普诺夫分析、时频分析以及庞加莱截面法研究系统非线性动力学行为。 表1 结构参数 表2 计算结果对比 (a)升速 (a)升速 (a)时域 首先不考虑轮盘内阻力,取表1中的结构参数对拉杆转子进行时域升降速(转速为100~2500 rad/s)响应特性分析,得到该拉杆转子1号轴承水平方向的量纲一位移-转速分岔图(图4)和李雅普诺夫指数图(图5),可知系统在升降速过程中的非线性动力学特性(分岔点、分岔类型和Lyapunov稳定性)存在明显差别,即降速过程中的转子响应在高转速区域的分岔特性比升速过程的更复杂。由图4a可知:①当转速小于606.5 rad/s时,拉杆转子系统保持稳定的周期1运动(P-1),这是由于系统在低转速区主要受不平衡力影响,仅存在转频成分;图5a中对应的Lyapunov指数均小于0,表明系统运动状态是Lyapunov稳定的,但该转速区间内的Lyapunov指数随转速的升高而变大。②转速ω≈606.5 rad/s时,升速过程中系统第一次出现倍周期分岔现象,系统运动模式由周期1进入周期2,Lyapunov指数约为0(A1点),验证了该转速点为倍周期分岔点。由图6可知转速为607 rad/s时,系统表现为周期2运动(P-2),此时,振动频率的基频和0.5倍频共同主导转子振动。③系统在ω≈678.9 rad/s时经过倍周期倒分岔返回到稳定的P-1,该转速处的Lyapunov指数约为0(A2点),图7表明升速过程中,系统在1149 rad/s做周期1运动。值得关注的是,ω>678.9 rad/s时,Lyapunov指数稍小于0,表明该转速区间内的系统可能存在双稳态解。综上,升速情况下,转速从100 rad/s升高到2500 rad/s时,系统响应依次发生如下演化过程:P-1→P-2→P-1。为便于对比分析升降速非线性振动,在分析降速情况时,将降速仍然视为随转速增加的运动过程。 (a)时域 对比分析降速和升速结果可知:在所关注的转速区间内,系统非线性振动特征存在明显区别,降速过程中的系统运动状态复杂且变化丰富:①ω<1101 rad/s时,降速过程中的系统运动状态、分岔特性及其变化过程与升速过程一致。②ω≥1101 rad/s时,升速过程中的系统保持稳定的P-1;在降速过程中,1101 rad/s≤ω≤1234 rad/s时,系统运动为周期3运动(P-3);1234 rad/s<ω≤1258 rad/s时,系统为拟周期运动,图5b中接近0的Lyapunov指数验证此转速范围内的系统处于拟周期运动状态;1258 rad/s<ω≤1306 rad/s时,系统运动为P-3;ω> 1306 rad/s时,系统保持稳定的拟周期运动。图5b中的B1、B2、B3、B4、B5为分岔点,相应的Lyapunov指数约为0。分别对比图6、图7中两种不同转速下的升降速响应特性可知,ω=607 rad/s时,升降速振动特性一致;ω=1149 rad/s时,升降速非线性振动特性存在明显差异性,升速过程中,系统响应在该转速处呈P-1运动,降速情况下为P-3运动,对应的频谱(图7c)中,0.3338倍频和基频处存在明显的谱峰,次同步振动幅值已经超过了同步振动幅值。 综合对比分析图4~图7可知,该拉杆转子系统在ω>1101 rad/s时出现双稳态振动,且存在2种不同的双稳态运动模式。1101 rad/s≤ω≤1234 rad/s、1258 rad/s<ω≤1306 rad/s时,系统响应在升速过程为周期1运动,在降速过程为周期3运动;1234 rad/s<ω≤1258 rad/s、ω>1306 rad/s时,系统响应在升速过程为周期1运动,在降速过程为拟周期运动。高转速下,盘式拉杆转子结构非连续及油膜力引入的非线性是导致双稳态振动特征的主要原因。 (a)升速 (a)升速 为进一步分析盘式组合转子系统出现的双稳态非线性振动,进行升降速下的转子振动频谱和响应分析。图8为转子系统升降速的非线性振动3D瀑布图,ω<1101 rad/s时,升降速的振动频率成分相同;1101 rad/s≤ω≤ 2500 rad/s时,升速工况的每个转速仅存在基频振动分量,而降速工况下的转速1101 rad/s处出现明显的频谱“跳跃”现象,频谱中除了含有转频成分外,还有一个明显小于 1/2 倍转频的次同步振动成分fn2且其幅值大于转频幅值,即油膜振荡主导转子振动。图9描述了升降速过程中系统响应的变化过程,亦可直观判断系统在1101 rad/s后出现双稳态振动。图10所示为升降速过程中转子系统1号轴承水平方向振动的单峰值(single peak value,SPV)以及最大振动位移-转速曲线,系统在606.5 rad/s ≤ω≤666.8 rad/s时发生半频涡动失稳即P-2运动;降速过程中,系统在1101 rad/s时发生振荡失稳和“非线性跳跃”,而升速过程中则不存在该非线性现象;系统在转速区间[1101 rad/s,2500 rad/s]存在双稳态振幅,再一次验证该盘式拉杆转子系统在特定转速区间出现“双稳态”振动现象。对于实际的机型而言,在动力学设计时须避免在工作转速范围内出现双稳态振动现象。 (a)振动单峰值 (a)升速 拉杆转子是高速、高负荷机型的核心部件,在全寿命周期内工况复杂多变,内阻可提高转子涡动的复杂程度。为了研究内阻效应,在动力学模型中考虑内阻力,得到该组合转子1号轴承处振动响应分岔图(图11)。 对比分析升/降速计算结果可知,转子在升降速过程中的振动特性不一致,其分岔类型、分岔点和运动稳定性存在明显差异:①转速ω<896 rad/s或ω≥1427 rad/s时,升降速过程中的系统响应一致,呈现P-1运动或拟周期运动,此转速区间内未出现振动失稳现象;②896 rad/s≤ω<1427 rad/s时,出现2.2节所述的非线性“双稳态”振动,与无内阻工况显著不同的是内阻效应下存在4种不同的双稳态运动模式,其中,896 rad/s≤ω<908 rad/s、920 rad/s<ω≤1017 rad/s时,双稳态运动模式为P-1(升速)与P-5(降速),908 rad/s≤ω≤920 rad/s为P-1(升速)与P-10(降速),1017 rad/s<ω≤1137 rad/s、1161 rad/s<ω<1427 rad/s为P-1(升速)与拟周期运动(降速),1037 rad/s<ω≤1161 rad/s为P-1(升速)与P-7(降速);③系统响应依次发生如下分岔:升速过程为P-1→拟周期运动,降速过程为P-1→P-5→P-10→P-5→拟周期运动→P-7→拟周期运动;④发生首次分岔失稳的转速为1427 rad/s(升速)和896 rad/s(降速)。造成此种差异性的主要原因是盘式组合转子存在非线性因子且具有迟滞惯性效应,在出现双稳态振动的转速区域,转子运动模式会处于何种状态主要由系统的初始条件决定,了解该转速区间振动特征对日趋高速化转子的动力学设计至关重要。 (a)升速 (a)时域 为验证上述非线性动力学响应特征,计算升降速过程中的Lyapunov指数(图12)。Lyapunov指数曲线图显示的周期运动与拟周期运动的变化趋势与图13中对应的分岔图相符,系统在较高转速时均处于拟周期运动状态,相应的Lyapunov指数接近于零。图13~图15所示为典型转速(896 rad/s、1149 rad/s和1330 rad/s)下的时域、轨迹、庞加莱截面和频谱,可直观判定系统在降速过程中的运动状态分别为P-5、P-7和拟周期运动,此时,次同步振动分量主导转子运动。 (a)时域 (a)时域 图16所示为升降速过程中含内阻组合转子系统1号轴承处的振动响应单峰值以及最大振动位移-转速曲线。系统在升降速过程中均发生振动响应“非线性跳跃”;在较高或较低转速区间内,升降速过程中转子系统的振动响应一致;系统在转速区间 [896 rad/s,1427 rad/s)存在双稳态振幅,表明该盘式拉杆转子系统在内阻作用下仍在特定转速区间出现“双稳态”振动。为避免转子在受到外界扰动后发生双稳态振动故障,工作转速和出现双稳态振动的起始转速之间应有足够的裕度。 (a)振动单峰值 通过频域响应分析得到转子1号轴承处非线性振动3D瀑布图(图17)。除了转速区间P1(896 rad/s≤ω<1427 rad/s)外,系统升降速过程中的振动频率成分相同;P1的转速区间内,升速过程中的振动响应仅含有转频成分,降速过程中的振动成分复杂,包括转频fr、次谐波频率fn1、fn2、fn3(fn3=fn1+fn2)、fn4(fn4=2fn1+fn2)成分、少量的2倍频成分,其中,次谐波fn3的振幅最大。大振幅油膜振荡使得转子振动剧烈,导致振动响应发生“跳跃”现象。 (a)升速 为揭示内阻对组合转子非线性动力学特性的影响规律,对比分析3.1节、3.2节的数据并提取关键非线性动力学特征参数,如表3所示,表中的半频涡动失稳视为第一次失稳,振荡失稳视为第二次失稳。 表3 非线性动力学特征参数 对比分析有无内阻情形下组合转子动力学特征参数可得如下结论:①转子系统在内阻作用下,升降速过程中均不再出现第一次失稳(失稳转速为606.5 rad/s),但升速过程中出现第二次失稳;②内阻使第二次失稳的起始转速明显向低转速方向移动,降速过程中的第二次失稳转速从1107 rad/s降至896 rad/s,升速过程中的第二次失稳转速从无到有,为1427 rad/s;③内阻使运动序列发生明显变化,但系统运动模式最终均进入拟周期;④内阻使升速过程中出现非线性振动响应、频谱“跳跃”;⑤内阻使出现非线性“双稳态”振动现象的转速区间长度缩小。 图18所示为升降速过程中1号轴承振动响应均方根值-转速曲线,将图中曲线与图4、图11相应的分岔曲线对比可知:内阻不改变涡动频率为转频的同步振动响应幅值,即系统的运动为纯同步振动时,有无内阻不影响其振动响应,这与文献[16]采用Jeffcott转子研究线性化转子轴承系统内阻效应所得振动规律相符,说明本文的研究方法正确,相应的研究结论可为转子设计提供参考。然而,内阻显著影响转子系统的非线性涡动,使降速过程中的非线性跳跃提前出现。此外,文中的双稳态响应与文献[14]采用相似转子所得加减速测试结果具有非常相似的特征。 图18 1号轴承振动响应曲线 图19 组合转子测试台 图20 升降速过程中转子振动位移曲线 图21 振动信号频谱图 为定性说明所得结论是有效的,本文开展周向拉杆组合转子升降速实验。如图19所示,试验转子由直流电机驱动,两端轴承均为滑动轴承。采用电涡流位移传感器采集振动信号,振动位移曲线如图20所示,由图可知,转子在第一阶临界转速1950 r/min附近存在明显的峰值。升降速过程中,振动随转速的变化趋势基本一致,除了在第一阶临界转速附近略有波动,这主要是由于在共振区域激起了固有频率模态,导致振动波动大。为进行组合转子频谱分析,对稳态响应进行快速傅里叶分析。图21中的转频及其倍频占主导,未发现分频振动分量。存在倍频成分的主要原因是转子与电机之间的联轴器、两端轴承之间均存在一定的不对中与角不平衡,以及转子存在初始轴弯曲。以上分析均表明实验转子在所测转速区间内未出现振动双稳态现象,这与本文所研究转子在一定转速下不存在的结论一致,定性说明本文所得结论具有合理性。 (1)建立的拉杆组合转子非线性动力学模型考虑了轮盘非线性接触、非线性油膜力、内阻效应,可用于分析含内阻的组合转子非线性动力学响应。 (2)组合转子有无内阻时,升降速过程中均出现明显的非线性“双稳态”振动特征,但内阻使非线性“双稳态”动力学转速区间明显向低转速方向移动。为有效预测出现双稳态振动的转速区间,在动力学分析时须考虑内阻效应,以确保转子在不同工况下均平稳安全的运转。 (3)内阻可抑制转子在低速工况下的失稳,但使转子在高转速下发生的振荡失稳提前出现,即高低转速存在不同的内阻效应,内阻使第二次失稳的转速点明显前移。 (4)内阻使转子系统运动序列发生明显变化,但最终在高转速下可进入拟周期运动;内阻在一定条件下可使升速过程中出现非线性振动响应、频谱等跳跃,并使非线性跳跃现象提前。 (5)内阻不改变以基频为主的纯强迫振动(同步振动),即有无内阻不影响其振动响应;在分析转子低速工况下的振动特性时可忽略内阻的影响;高转速非线性动力学系统的涡动复杂,须考虑内阻效应,以有效预测转子双稳态振动特性,保障转子平稳安全运行。

1.2 内阻力
1.3 转子系统运动方程



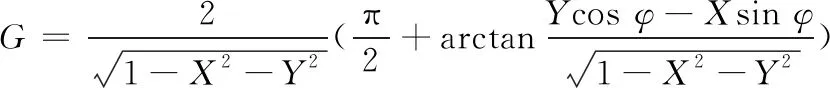
2 动力学模型
3 数值仿真与算例分析
3.1 无内阻组合转子的双稳态升降速特性


3.2 含内阻的组合转子双稳态升降速特性


3.3 对比分析与讨论





4 结论

