剪滞效应对复合材料固化变形影响的数值分析
乔 巍 姚卫星,2
1.南京航空航天大学飞行器先进设计技术国防重点学科实验室,南京,210016
2. 南京航空航天大学机械结构力学及控制国家重点实验室,南京,210016
0 引言
先进复合材料凭借比强度高、比模量高等优点在航空航天领域获得了广泛应用[1-2]。固化后的复合材料构件实际形状往往与理论设计形状存在一定偏差,该偏差称为固化变形。复合材料的固化变形不仅增加了装配难度,而且提高了制造成本。因此,建立复合材料构件固化变形的分析模型,并研究固化变形的机理,对于提高复合材料结构的设计与制造能力都具有重要意义。
数值仿真广泛应用于复合材料固化变形的模拟,其核心是固化本构模型。BOGETTI等[3]假设固化过程中树脂模量与固化度成线性关系,提出线弹性本构模型。该本构模型在国内外有较多应用。郭章新等[4]通过该模型模拟了带金属内衬的纤维缠绕复合材料圆筒固化过程中残余应力的变化规律。马云荣等[5]基于该模型模拟了曲面构件的固化过程,结果表明考虑材料性能的变化使模拟结果更加精确。WHITE等[6]和ZOCHER等[7]考虑了材料的黏弹性,并采用广义Maxwell 模型描述固化过程中材料的松弛刚度。闵荣等[8]和张江涛等[9]采用黏弹性本构模型模拟了固化过程中残余应力的发展。SVANBERG等[10-11]提出Path-dependent本构模型,该模型是黏弹性本构模型的简化版,假设橡胶态阶段的材料转换因子为零,玻璃态阶段的转换因子为无穷大。笔者对比了上述3种本构模型,结果表明Path-dependent模型和黏弹性本构模型预测的固化变形与试验结果吻合良好,但线弹性本构模型的预测结果误差较大[12]。
目前剪滞效应对固化变形的影响以理论研究为主。WISNOM等[13]研究发现,剪滞效应减小了玻璃化转变前热和化学收缩引起的回弹变形。王乾等[14]采用剪滞理论和弯曲理论构建L形构件回弹变形的理论模型,考虑了构件直边的约束作用带来的影响。
剪滞效应的研究仍存在一些有待解决的问题,如结构参数、剪滞效应及固化变形之间的关系及机理。通过数值模型的量化分析,可以更深入地揭示剪滞效应的机理。因此,本文通过分析复合材料固化过程中热、化学收缩及材料性能之间的多场耦合,建立复合材料固化变形的三维数值仿真模型,通过与试验结果的对比,检验所建模型的合理性,最后研究剪滞效应的影响及机理。
1 理论模型
复合材料的固化过程涉及物理-化学-材料的多场耦合。树脂化学反应释放热量,温度场和化学场构成了强耦合关系,而温度场与材料性能及应力-应变场之间为弱耦合关系。在有限元计算中,强耦合采用直接耦合法分析,弱耦合采用顺序耦合法分析。因此,将固化过程的模拟分成热-化学和应力-变形两个模型,通过时间步的迭代来模拟温度-固化度-应变-应力的产生和发展。
1.1 热-化学模型
固化过程中复合材料构件内部的热量不仅包括热压罐传递的热量,还有树脂化学反应释放的热量。在温度场和化学场的强耦合作用下,各向异性复合材料的三维热传导方程为[3]
(1)
(2)
式中,t、T分别为时间和温度;ρp、cp分别为复合材料的密度和质量热容;x、y、z分别表示沿着纤维方向、垂直纤维方向和厚度方向;kx、ky、kz为热导率;Q为内热源项[3];HR为单位质量树脂完全固化释放的热量;ρr、Vf分别为树脂的密度和纤维的体积含量;α、dα/dt分别为固化度和固化率。
本文所用LT-03A树脂的固化动力学方程为
(3)
式中,ΔE为活化能,ΔE=1.016×105J/mol;A为频率因子,A=2.34×1012min-1;R为普适气体常数。
1.2 应力-变形模型
1.2.1固化本构模型
固化过程中纤维性能几乎不变,复合材料的热力学性能由树脂决定。根据固化过程中树脂材料状态的不同,以凝胶点和玻璃化转变点为界,将固化过程分成黏流态、橡胶态和玻璃态3个阶段,如图1所示。

图1 固化过程中复合材料状态的变化
大部分学者认为,凝胶前树脂具有较强的流动性,复合材料不能保存残余应变和残余应力[10]。对于凝胶后的材料性能,Path-dependent本构模型假设复合材料的刚度系数在每个材料状态内是常数,在玻璃化转变点呈阶梯变化,该模型的应力增量方程如下[10,15]:
(4)
(5)
(6)
(7)
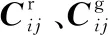
正交各向异性复合材料的刚度系数矩阵可通过工程常数计算,详见文献[8]。玻璃态工程常数可以通过试验测量,但橡胶态工程常数很难测量。通常认为固化过程中沿纤维方向上的弹性模量E11保持不变,对于其他方向的模量,假设橡胶态和玻璃态弹性模量满足以下关系:
(8)
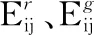
试验研究证实[17],橡胶态复合材料的泊松比ν23近似为1。
1.2.2化学收缩模型
固化过程中树脂化学反应会引起树脂体积收缩,环氧树脂化学反应的体积收缩率在2%~7%之间,表1给出了两种典型环氧树脂化学反应的体积收缩率。本文采用试错法,假设LT-03A树脂化学反应的体积收缩率为6%。

表1 两种典型环氧树脂化学反应的体积收缩率
通过树脂化学反应的体积收缩率可计算出树脂化学收缩应变[19]:
(9)
式中,ΔVsh为树脂化学反应的体积收缩率;εsh为树脂化学收缩应变。
复合材料沿纤维方向的化学收缩系数γ1由纤维主导,该系数非常小,通常假设γ1≈0,复合材料垂直纤维方向的化学收缩系数[19]:
γ2=γ3=(1+νr)(1-Vf)εsh
(10)
式中,γ2、γ3为复合材料垂直纤维方向的化学收缩系数;νr为树脂的泊松比。
GARSTKA等[17]认为化学反应主要发生于橡胶态阶段,此时树脂可看作不可压材料,其泊松比近似0.5。
1.3 数值仿真流程
建立复合材料固化变形的三维有限元仿真模型,该模型由热-化学模型和应力-变形模型构成。分析过程中,先进行瞬态热分析,计算出构件内每个节点的温度、固化度及固化率,应力-变形模型根据传递的温度和固化度更新材料性能,并计算材料的非机械应变,然后进入软件的主程序计算残余应力和变形。进入下一个时间步,直至固化结束。固化变形的数值仿真流程如图2所示。
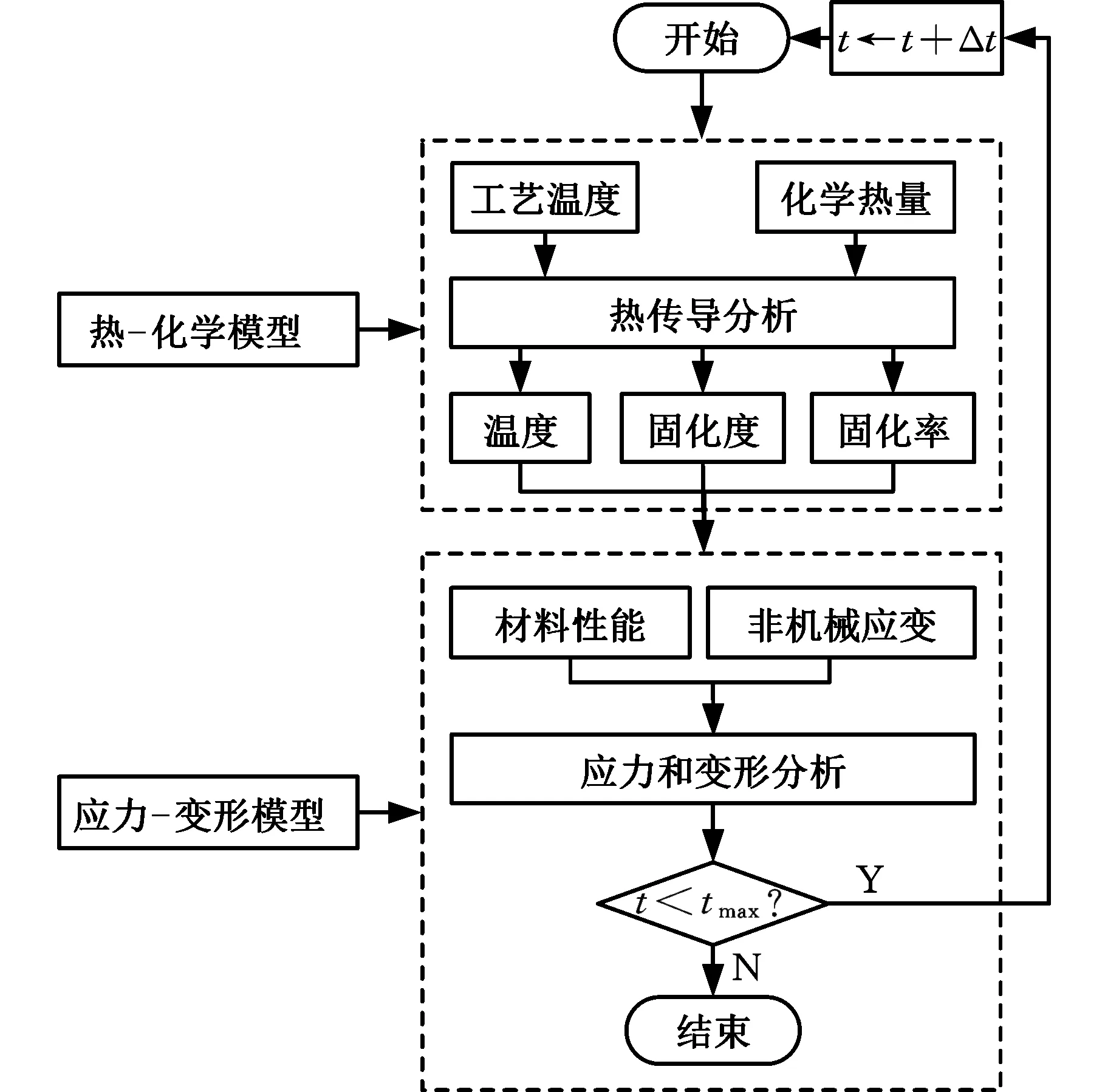
图2 复合材料构件固化变形的数值仿真流程
利用ABAQUS有限元软件的用户子程序实现上述数值分析。采用UMATHT子程序定义化学反应产生的热量,利用UEXPAN子程序定义热和化学收缩产生的非机械应变,并通过UMAT子程序实现对材料本构方程的自定义。
2 试验
2.1 材料与工艺
预浸料选用中航复合材料有限责任公司生产的ZT7G/LT-03A。该复合材料的凝胶固化度为0.5,密度为1520 kg/m3,比热容为1050 J/(kg·K),沿着纤维方向和垂直纤维方向的热导率分别为5.6 W/(m·K)和0.56 W/(m·K),玻璃态力学性能见表2。采用热压罐、阳模固化成形,固化后单层厚度为0.125 mm,纤维体积含量为67%。固化工艺为:先以1.5 ℃/min升温至130 ℃,然后保温2 h,再以不大于2 ℃/min降至室温。真空袋压力不小于0.095 MPa,热压罐压力为0.6 MPa。复合材料沿纤维方向的CTE由纤维主导,通常非常小(约0.001×10-6/℃)[20],通过热膨胀仪测定垂直纤维方向的CTE为22.5×10-6/℃。

表2 复合材料ZT7G/LT-03A的玻璃态力学性能
2.2 试件
试件为L形复合材料构件,共15件。试件直边宽度为50 mm,长度为200 mm,转角半径有4、8、12 mm 3种类型,如图3所示。试件铺层为[0/90]ns,n为1、2、4,试件厚度有0.5、1.0、2 mm 3种类型。试验矩阵如表3所示。
2.3 变形测量
目视检查了所有试件,在试件直边上没有发现明显的翘曲变形,说明模具表面粘贴的脱模布有效削弱了模具与复合材料间的相互作用力,因此本文的研究忽略了模具作用的影响。
采用非接触式三维光学扫描仪测量试件的固化变形。扫描仪获取试件外形面的离散点(精度为0.2 mm/m),然后将这些离散点导入CATIA软件,选取合适区域的离散点,基于最小二乘法拟合出平面A和平面B,如图4所示。为了排除边缘干扰,尽量选择相对平整的中心区。读出平面A和B的夹角θ,计算出试件的回弹角:

(a)试件的制备

表3 试验矩阵
Δθ=90°-θ
(11)
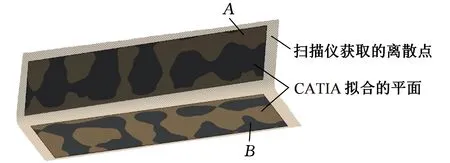
图4 试件变形的测量
3 仿真模型的建立及验证
3.1 有限元模型
根据对称性,取1/4几何划分网格,单元类型选择三维八节点六面体单元。边界条件为:脱模前,约束构件底面节点的垂向位移,放开切向位移约束;脱模后,放开构件底面节点的位移约束,使构件自由变形,如图5所示。
3.2 仿真模型的验证
表4给出试件回弹角的预测结果与试验结果的对比。

(a)脱模前

(b)脱模后

表4 试件回弹角预测结果与试验结果的对比
4 剪滞效应的影响分析
4.1 剪滞效应的表征方法
在玻璃化转变前,复合材料的层间剪切模量非常小,构件厚度上的收缩会使层间发生滑移,称为复合材料的剪滞效应,如图6所示。玻璃化转变后,材料的层间剪切模量通常会增大两个量级,复合材料不会再发生剪滞效应。
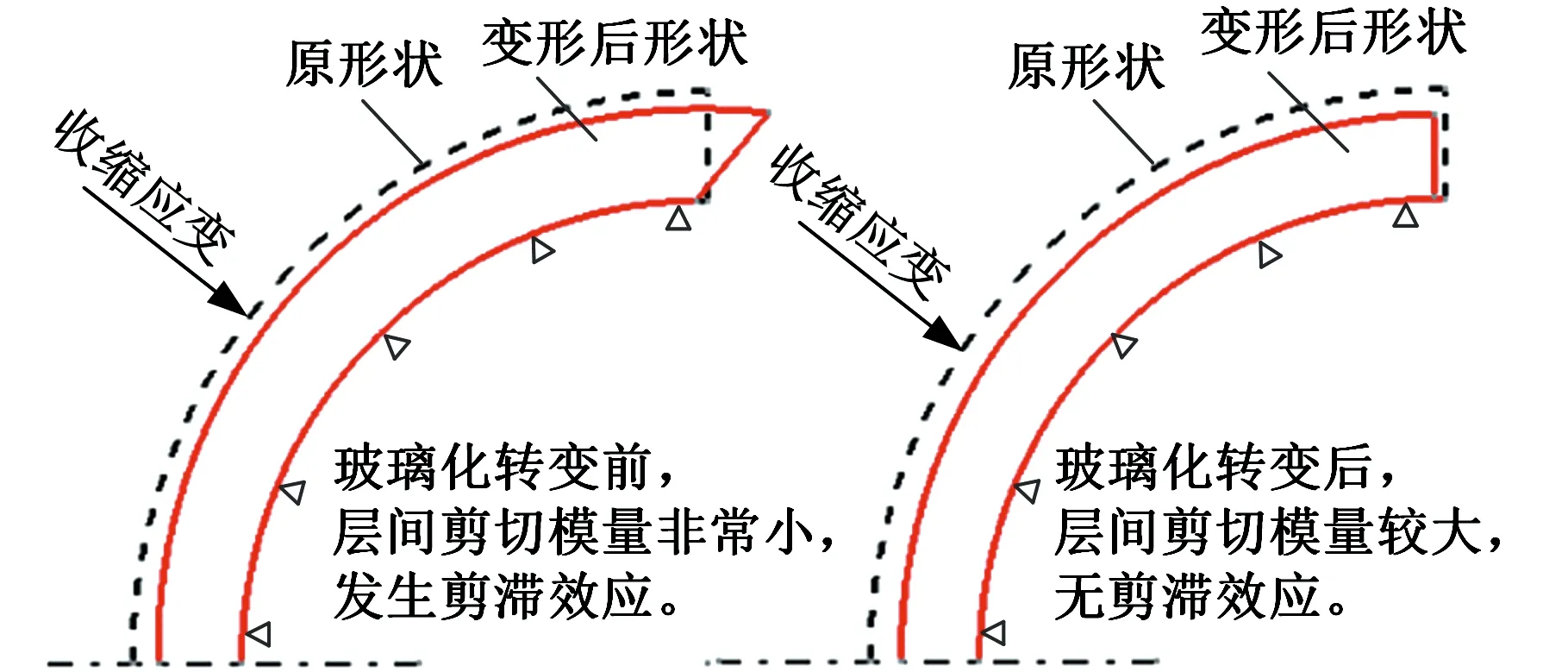
图6 复合材料构件的剪滞效应
本文定义了一个剪滞角Δθs-l,用于量化表征剪滞效应的强弱程度。将固化过程中玻璃化转变点的构件转角区端面与原形状端面之间的夹角记为剪滞角,如图7所示。采用剪滞角的大小来定量描述剪滞效应的强弱,剪滞角越大,则剪滞效应越强,反之,则剪滞效应越弱。
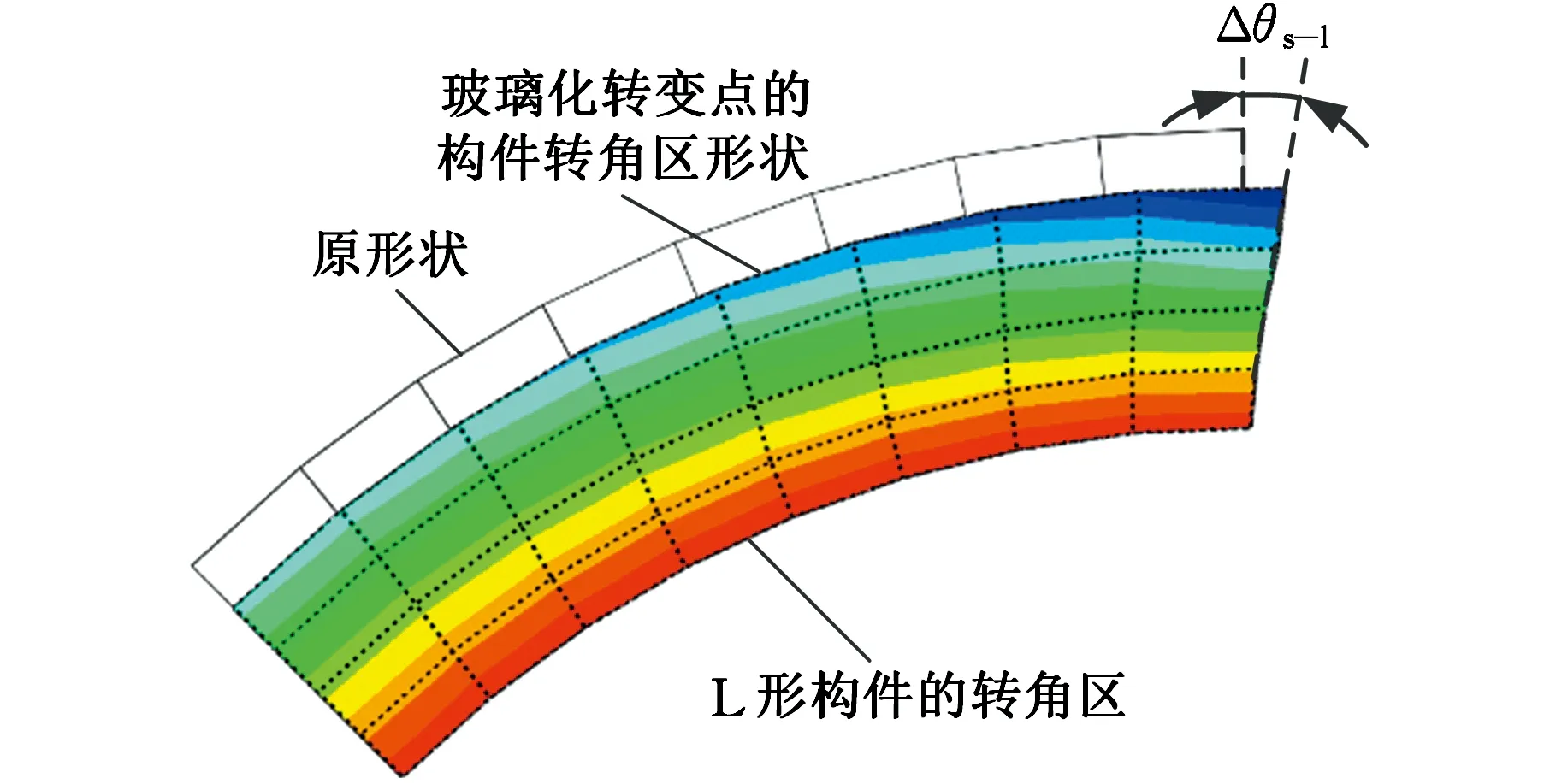
图7 复合材料构件的剪滞角

图8 剪滞角随构件厚度的变化
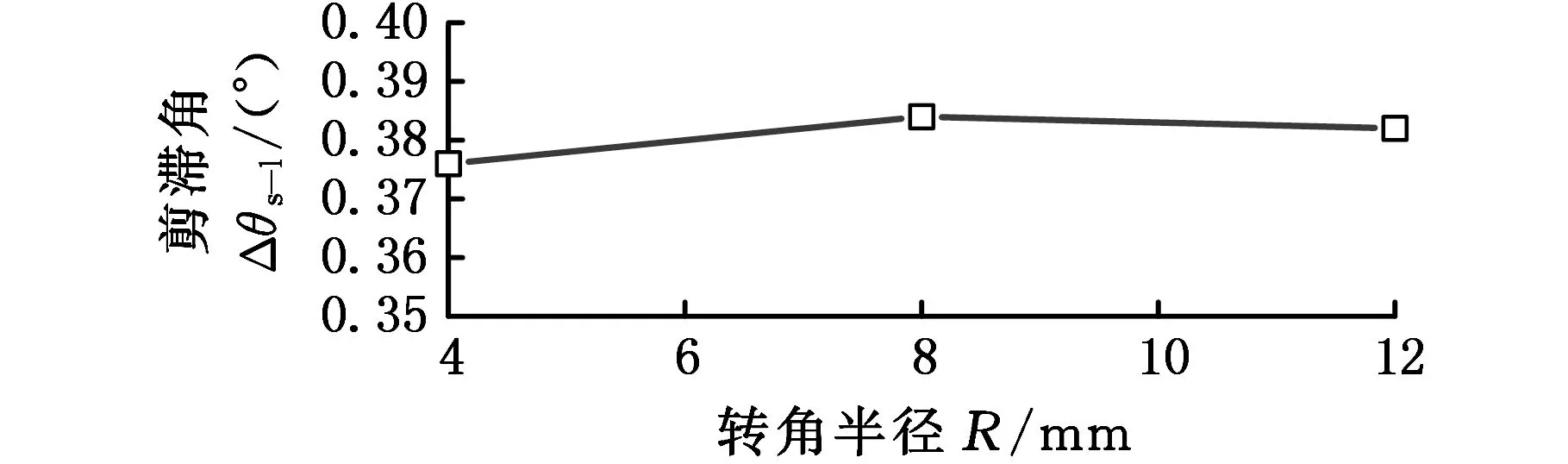
图9 剪滞角随构件转角半径的变化
4.2 结构参数对剪滞效应的影响
图8和图9分别给出剪滞角随构件厚度和转角半径的变化曲线。结果显示,随着构件厚度的增大,剪滞角逐渐增大,但构件转角半径变化时,剪滞角的变化很小。研究表明,剪滞效应随构件厚度的增大而增大,而转角半径对其影响很小。
4.3 剪滞效应对固化变形的影响

图10 剪滞角和回弹角随构件厚度的变化
图10给出剪滞角和回弹角随构件厚度的变化。图中结果显示,随着剪滞角的增大,回弹角逐渐减小。可解释为,当固化过程处于橡胶态阶段时,在剪滞效应的影响下构件的层间发生了滑移,该滑移消耗了构件的部分收缩应变能,那么根据能量守恒理论,用于构件回弹变形的收缩应变能就减少了,因此构件的回弹角就变小了。研究表明,构件的回弹角随着剪滞效应的增强而减小。
4.4 剪滞效应对仿真模型计算准确性的影响
BAPANAPALLI等[20]提出一个简化的数值模型,模型中材料的CTE包含了真实CTE和化学收缩等效的CTE两个部分,计算降温引起的固化变形。图11给出了不同数值模型的预测结果与试验结果的对比。结果表明,本文所建模型的预测结果与试验结果吻合良好,但Bapanapalli模型的预测结果误差较大,不能反映固化变形随构件厚度的增大而减少的变化趋势。可解释为,Bapanapalli模型没有模拟降温前的固化过程,不能模拟发生于降温前橡胶态阶段的剪滞效应。因此,Bapanapalli模型不能反映剪滞效应对固化变形的影响,很难给出准确的预测结果。

图11 不同数值模型的预测结果与试验结果的对比
5 结论
(1)建立了复合材料固化变形的三维数值仿真模型,通过预测结果与试验结果的对比,证明所建模型具有较高的计算准确性。
(2)基于所建仿真模型,量化分析了剪滞效应的影响。结果表明,剪滞效应随构件厚度的增大而增强,但构件转角半径对剪滞效应的影响很小;剪滞效应是影响构件固化变形的重要因素,固化变形随着剪滞效应的增强而减小。
(3)对比了本文所建数值模型与文献中数值模型,结果表明,若不考虑剪滞效应,数值模型很难获得准确的预测结果。该研究成果对推动复合材料固化变形数值仿真模型的发展具有一定的指导意义。

