基于学习进阶理论的高中物理教学设计——以“功”的教学为例

赖世锵 曾通宝

(1.广东省广州市仲元中学，广东 广州 511400；2.广东省中山市龙山中学，广东 中山 528471)

1 引言

学习进阶是对学生在某一时间跨度内学习和探究某一主题活动时，依次进阶、逐层深化的思维方式的描述，[1]是刻画学生在对核心科学概念形成更复杂的理解时可能遵循的潜在认知途径。笔者根据《普通高中物理课程标准(2017年版)》对核心素养培养的要求，以学习进阶理论为指导，设计、实施物理教学，对于学生物理观念的培育与科学思维的发展有着重要的促进作用。

2 学习进阶层级

北京师范大学郭玉英教授等对学习进阶进行了深入研究，提出了科学概念理解发展的层级模型，学习进阶可分为经验、映射、关联、系统、整合等5个发展层级，在物理课堂教学中可以根据这5个层级来组织课堂教学活动。通过创设情境，设计一系列的教学活动，培育学生的物理观念，发展科学思维。在教学设计中需要思考以下问题：学生概念发展的起点和终点分别是什么？从起点到终点，需要经历哪些必要的中间状态？学生怎样才能顺利跨越这些中间状态，需要的认知负荷是什么？如何通过教材分析、学情分析设置进阶目标？如何制定学习进阶的发展层级？笔者以“功”的教学为例，展示具体的教学设计及其实践。

3 “功”的教学分析

3.1 教材分析

功是衔接力与能量的重要桥梁，是高中物理学习的基础，在高中物理教材中处于十分重要的地位，学习的效果会直接影响到动能定理、机械能守恒定律、能量守恒定律等的学习。

3.2 学情分析

在初中阶段，学生已经学过功的概念及其简单计算，但是只涉及力与运动方向相同情况下力所做的功，在知识学习上学生存在一定的思维定势，因此教师要引导学生积极思考，可以从功能关系入手，引导学生理解功的含义，掌握功的计算公式，理解摩擦力做功的特点。

3.3 进阶起点分析

在对功概念的认识上，学生认为：由于物体具有能量，所以能够对外做功，他们对功已有一定的了解。在力与运动方面，学生较熟练掌握了物体的受力与运动分析，并能灵活运用牛顿运动定律。在思考问题时，高一学生常常需要将问题与生活经验等相联系，从而实现从形象思维向抽象思维的过渡。因此，在教学过程中需要创设情境，培育学生正确的物理观念，并把所学知识应用于实际问题，形成必备的知识与关键能力。

3.4 进阶目标预设

《普通高中物理课程标准(2017年版)》指出：理解功，分析物体移动的方向与所受力的方向不在一条直线上时，该力所做的功。[2]知道做功的两个必不可少的条件，明确功是标量，深入理解正负功的物理意义，并能灵活运用功的计算公式W=Flcosα去解决实际问题，会分析变力的功，并能够总结出摩擦力做功的特点。学生应该逐步形成功与能量观念，从能量的角度去思考、分析与处理问题，并对功能关系有一定的认识，为后续学习打下基础。

3.5 进阶点和进阶层级预设

根据学习进阶理论，需要合理设置进阶点，相邻进阶层级之间的跨度应该适中，为此，“功”的进阶点可以设置为4个(图1)。

图1

根据学习进阶层级模型，对“功”的层级描述如表1。

表1

3.5.1 进阶起点

教师创设情境，故意将讲台放在教室门口处，请一位学生来推讲台，但讲台很重，没推动。后来几个学生一起推，终于推动了。

师：刚才同学们对讲台有没有做功？

生：物体在力的作用下移动了一段距离，那么这个力就对物体做了功。一个同学推时没有推动讲台，没有做功。

设计意图：通过创设真实情境，设置进阶起点，回顾原有知识，提出问题，引发学生思考，引出课题，为本节课的学习做好铺垫。

3.5.2 进阶点1

(1)什么是功？怎样才算力对物体做了功？

(2)做功的两个必不可少的因素是什么？

师：分析图2中的4种情景，人是否对物体做了功？请大家思考与讨论，可从运动方向、作用力方向等方面进行分析。

图2

学生通过思考与讨论，设计并填写表2。

表2

生：(1)若在力作用下物体发生了位移，那么我们就说这个力对物体做了功。(2)描述做功有两个必不可少的因素，即力和在力的方向上发生了位移。

设计意图：创设生活情境，引导学生分析实例，通过模型建构、科学推理等，学会区分物理上的做功和生活上的“做工”，寻找做功的两个必不可少的因素，进一步理解功的概念，掌握核心知识，培养学生的科学思维能力。

3.5.3 进阶点2

教师提出问题：(1)如何计算功？当力与位移两者方向一致时，功的大小表达式是什么(图3)？方向不一致呢？能否通过力的分解或位移的分解来寻找功的大小？(2)功是标量还是矢量？正负号的含义是什么？(3)功的单位焦耳有何物理意义？

图3

图4

教师引导学生推导：当力F和位移l两者方向一致时，功的大小W=Fl。当力F和位移l两者方向成α角时，功的大小W为多少？

生：(1)通过分解力F，得到W=Fcosα·l=Flcosα；分解位移l，得到W=F·(lcosα)=Flcosα。由此可知，力对物体所做的功W=Flcosα。(2)力与位移都是矢量，但功是标量，且有正负之分。

设计意图:教师设置问题串，引导学生建构熟悉的模型，并进行科学推理，学生运用所学过的力或运动的分解去推导出功的计算公式，进一步加深对功的认识。

3.5.4 进阶点3

情境一：如图5所示，若用一水平推力缓慢地向左推物块，弹簧被压缩，突然撤去水平外力，物块被弹开，求弹簧弹力所做的功。

图5

学生讨论与交流：弹簧弹力时刻变化，W=Flcosα不再适用，该公式只适用于恒力所做的功。

情境二：如图6所示，一半径为R的粗糙圆形弯管放置在水平桌面上，现一小球以足够大的初速度在管内做圆周运动，求小球运动一周的过程中克服摩擦力所做的功，已知小球所受摩擦力f大小恒定不变。

图6

教师引导学生分析：f大小恒定，但运动方向时刻改变，属于变力做功，显然不能直接使用功的公式，这里可以运用微元法。把小球运动的路程分成无数小段，若设每小段长度Δx，那么每段运动均可近似看成直线运动，且运动方向与摩擦力方向始终相反，故这一小段元功ΔW=fΔx。在小球运动一周的过程中，其克服摩擦力的功可看成各元功之和，即W=f(Δx1+Δx2+……)=2πRf。

情境三：一质量为10kg的物块与橡皮筋相连并静止在粗糙水平面上，接触面间动摩擦因数μ=0.1。现施加一水平力F去拉橡皮筋，当橡皮筋伸长量为0.4m时，物块刚好动起来，此后继续拉动橡皮筋，于是物块缓慢运动了0.4m，试求拉力F所做的功。

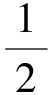
图7

情境四：如图8所示，一物块与橡皮筋相连，静止在光滑的水平面上。现施加一水平力F缓慢拉动木块，木块向前运动了x，试求此过程中F所做的功。

生：由于木块缓慢移动且橡皮筋的弹力是变力，这里可以用图像法求解。

师：是的，可用图像法处理。还有其他方法吗？橡皮筋的弹力是如何变化的？

设计意图：通过进阶问题设置，促进学生掌握功的计算方法，明确W=Flcosα只适用于恒力做功。再设计三个递进情境，让学生进一步掌握计算功的其他方法，如微元法、图像法、平均力法等。

3.5.5 进阶点4

(1)若物体同时受到多个力作用，如何求得总功？

情境一：一物块静止在斜面体上，现施加一水平向右拉力F，斜面体与物块相对静止一起向右匀速运动，在运动一段距离l的过程中，分析各力做功的情况，总功是多少？

教师点拨：各力所做功容易求解，但如何求得多力的总功？

生1：先求出各力的功，再求其代数和。

生2：先求出合外力，再求合外力所做的功。

师生共同总结：通常可以用上述两种方法求总功，用公式表示为W=W1+W2+W3+……，W=F合lcosα。

(2)摩擦力做功有什么特点？

情境二：试分析以下4种情境中摩擦力做功的情况。

图9

生：对于情境甲，物体没动，位移为零，静摩擦力做功为零；对于情境乙，人与小车相对静止，小车与人之间的静摩擦力为零，摩擦力做功为零；对于情境丙，物块与小车两者一起向右作匀加速直线运动，并保持相对静止，在此过程中车对物块的静摩擦力做正功，物块对车的静摩擦力做负功；对于情境丁，物块B向左运动，受到物块A向右的滑动摩擦力，并产生了一段位移，A对B的滑动摩擦力做了负功，虽然A受到B向左的滑动摩擦力，但是此滑动摩擦力不做功。

教师引导学生总结，通过上述分析，我们可以得到如下结论：无论静摩擦力还是滑动摩擦力都可能对物体做正功、负功或不做功。

师：从以上分析，请问一对摩擦力做功的代数和为零吗？

生：不一定为零。在情境丙中，一对静摩擦力做功的代数和为零；在情境丁中，一对滑动摩擦力做功的代数和不为零。

设计意图：通过实例分析，总结出计算功的两种方法，并学以致用。通过比较与分析，学生掌握了摩擦力做功的特点，模型建构、科学推理等科学思维能力也得到培养。

4 结语

笔者根据核心素养的培养要求，基于学习进阶理论，针对功的教学进行设计，从学习进阶的五个层级来组织教学活动，层层递进，逐渐深入。同时根据学生思维发展特点，创设情境和问题串，提升学生的物理学科核心素养。