关于动态平衡问题的研究

朱顺明 蒋建明

(江苏省天一中学，江苏 无锡 214101)

动态平衡问题是指通过控制某些物理量的变化，使物体的状态发生缓慢变化，其中“缓慢”是指物体运动的速度极小，可以物体在变化过程中处于平衡状态，即动态平衡。此类问题在高考试题中频频出现，也是力学的难点。处理动态平衡问题的关键是把“动”化为“静”，“静”中求“动”。从物体受力的个数来看，目前以三力作用下的动态平衡问题居多。通常我们采用解析法、图解法、相似三角形法等来处理。本文将呈现五种不同的解题方法，对两力夹角一定的动态平衡问题进行研究，探讨题中两力的大小变化情况，丰富解决动态平衡问题的方法。

1 问题呈现

例1：如图1所示，置于地面的矩形框架中用两细绳拴住质量为m的小球，绳B水平.设绳A、B对球的拉力大小分别为F1、F2，它们的合力大小为F，现将框架在竖直平面内绕左下端缓慢旋转90°，在此过程中( )。

图1

A.F先增大后减小

B.F始终不变

C.F1先增大后减小

D.F2先增大后减小

分析：该题旨在考查学生对力的合成与分解的深刻理解，尤其关注合力与分力关系的分析。本题中合力一定、两分力夹角也一定，要求判断分力大小的变化情况，从答题的情况来看，有学生对此题显得束手无策，究其原因是我们平时讨论的都是如例2的合力一定、两分力间夹角变化时分力大小的变化问题。

例2：如图2所示，某同学在单杠上做引体向上，以下四个选项中双臂用力最小的是( )。

图2

分析：双臂拉力的合力一定，大小等于该同学所受的重力，双臂的夹角越大，所需拉力越大，当双臂平行时，双臂用力最小，故选项B正确.

那么在两分力夹角不变时分力大小变化问题又该如何解决呢？

2 问题解决

2.1 利用DIS进行实验

如图3所示，利用DIS研究框架在竖直平面内绕端点O逆时针缓慢旋转90°的过程中F1、F2大小变化的情况。在绳A、B处分别连接力传感器1和2，通过数据采集器实时记录拉力随时间的大小变化并传送给计算机，此时屏幕上显示出如图4所示的F1-t和F2-t图线。从图像中可以看到F1从最大值开始一直减小到零，F2从某一值开始先逐渐增大到最大，然后逐渐减小到某一值，并且通过比较发现F1和F2的最大值相等。

图3

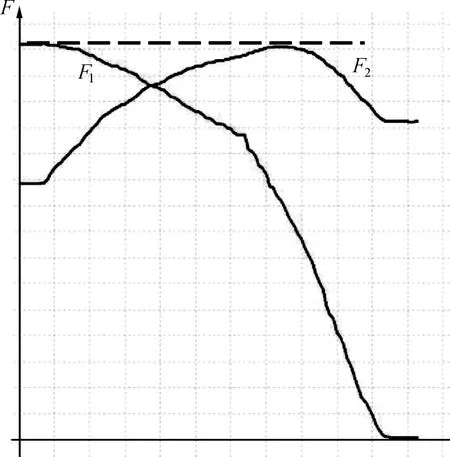
图4

2.2 应用平行四边形定则

对小球进行受力分析，它受到重力、拉力F1和拉力F2的作用。利用平行四边形定则，画出F1和F2的合力F合，F合与重力等值反向，保持不变。在保持F1和F2的夹角θ一定的情况下，画出拉力在不同方向的平行四边形(图5)，比较矢量线段的长短，可得出结论：将框架在竖直平面内绕左下端缓慢旋转90°，在此过程中拉力F1一直减小，拉力F2先增大后减小。

图5

2.3 运用画圆法

我们继续研究图5，由于F1和F2的夹角θ一定，在矢量三角形中，F1和F合间的夹角为π-θ，且F合一定，就联想到在同一圆中同弦所对的同一侧的圆周角相同。

如图6所示，画一个圆，表征F1、F2、F合的线段在同一外接圆上。由图6可知：拉力F1开始时为圆的直径，是最大值，然后逐渐减小；而拉力F2先增大，当F1处于水平方向时，这时F2就为圆的直径达到最大值(与F1的最大值相等)，然后又逐渐减小到mg。

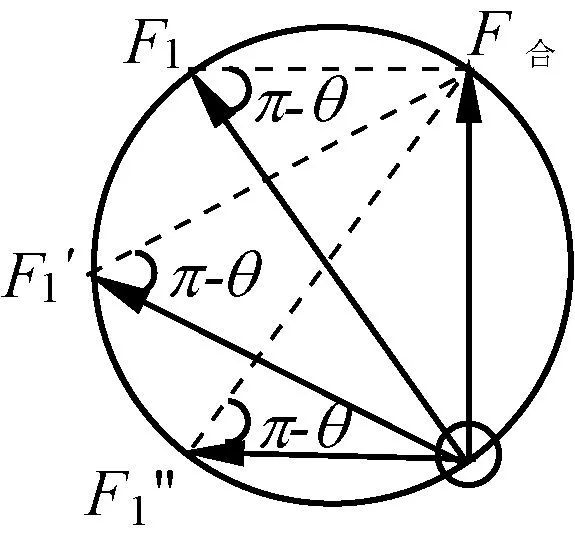
图6

2.4 运用逆向思维法

例1情境是合力不变、保持拉力F1和拉力F2夹角θ不变，F1和F2整体作逆时针旋转。现在我们可以采用逆向思维法，在拉力F1、F2方向不变的情况下，以O为圆心、F合大小为半径作1/4圆弧，让合力F合顺时针旋转至水平的过程中作出相应的平行四边形，从而得到如上所述的F1、F2大小变化关系(图7)。

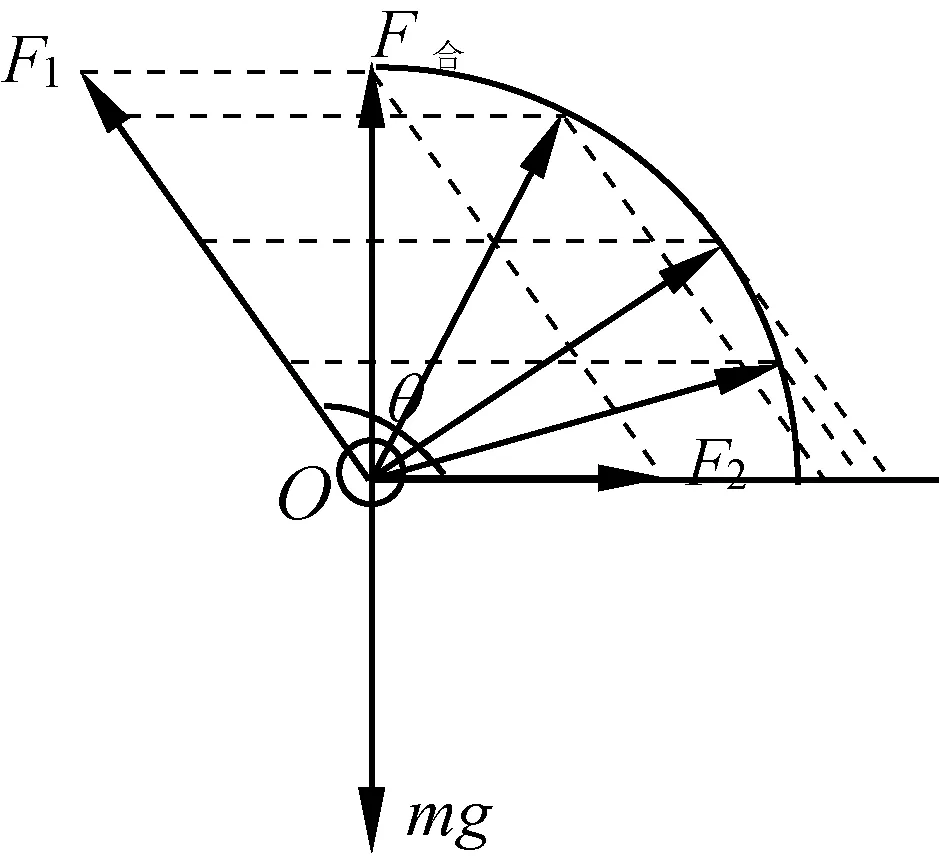
图7

2.5 应用正弦定理

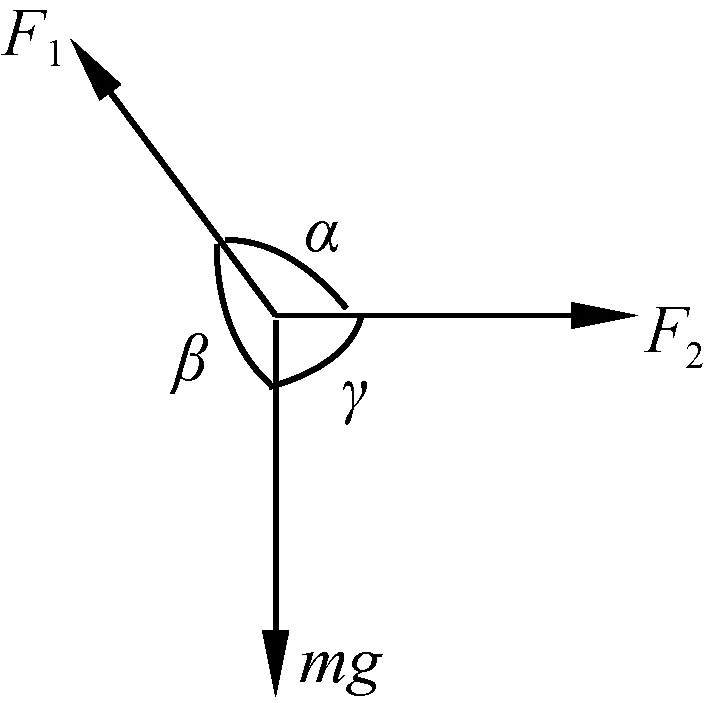
图8

3 结语

笔者以一道动态平衡题为例，用一题多解的方式让学生经历理论与实验相结合的探究过程，让学生深刻理解与掌握处理动态平衡问题的方法。教师以提升学生的认知能力为目标，以物理方法为中心，积极调控概念与知识的学习，从而达成不断优化的教学设计与精妙的解题思路。