SOLO分类理论在高中物理复习中的应用①
——以“圆周运动”为例
李国榕 唐 政 张念依 邓楚楚 林 琪 叶晴莹
(1.福建师范大学物理与能源学院,福建 福州 350117;2.福建省福州市金山中学,福建 福州 350008)
无论对于哪一学科而言,复习课都是教学的重要组成部分,运用科学有效的教学方法,能更好地培养学生的核心素养、提高学习效率。在同一个班级中,出现学生学习水平不平衡是正常现象,教师在复习课时可以根据学生的不同学习水平采取不同的教学方法,提高学生的复习效率,但如何将学生的水平进行划分又是教师在教学过程中要面对的难题。
中学物理教育应注重对学生科学思维能力的培养,针对不同学习水平的学生采用合适的教学方法是提高学生学习能力的关键。将SOLO分类理论运用于复习课的教学中,有助于教师分析学生学习水平层次,建立最近发展区,提高学生的学习能力。
1 SOLO分类理论简介
SOLO(Structure of the Observed Learning Outcome)分类理论由澳大利亚心理学家比格斯(J.B.Biggs)率先提出,可译为“可观察的学习结果的结构”,他将学生的学习结果由低到高分为五个层次水平。
(1)前结构水平:面对问题时学生无法理解、解释或者答非所问。
(2)单点结构水平:学生能从问题中找到一个解题条件,直接从该单一条件得出答案。
(3)多点结构水平:学生能够找到多个解题条件,联想到相关的知识,但不能将这些知识进行有机整合。
(4)关联结构水平:学生能够从多个角度对问题进行分析,能将各种有效信息结合起来思考,解决较为复杂的问题。
(5)拓展抽象水平:学生能够将接触过的问题迁移到新的情景中,并且能够得到具有开放性的结论,概括出更抽象的本质属性,使问题本身的意义得到拓展。
这五个水平层次体现了学生对事物的理解阶段:我不理解它——我知道了一个方面——我知道了大多数——我知道它们是怎么结合到一起的——我明白这个可以在多种情况下运用。
2 SOLO分类理论在“圆周运动”复习课中的应用
SOLO分类理论将学习者的学习水平划分成为层级结构,意味着学习者的学习水平是由低级向高级、形象到抽象逐步发展的。教师可依据学生的学习表现判断学生处在哪个层次水平,从而设计物理教学,本文以鲁科版必修二第四章“圆周运动”的复习课为例。
2.1 前结构水平
在学习完“圆周运动”后,教师要想了解学生的学习水平,可以先通过基础知识开始,向学生提问:什么是匀速圆周运动?若有学生连这个问题都回答不出来,或者回答根本就与匀速圆周运动无关,教师可判断该学生处于前结构水平。
教师可以从基本概念入手,帮助学生建立基本的知识体系。首先可以列举一些生活中圆周运动的实例:摩天轮、过山车、月球绕地球运转等,再引出匀速圆周运动的定义:在任意相等时间内通过的弧长都相等的圆周运动叫做匀速圆周运动。通过实例与图像相结合,让学生逐渐建立起圆周运动的基本概念,顺利将学生推向更高的学习水平。
2.2 单点结构水平
处在单点结构水平的学生,在物理学习上主要表现为:能用一个相关知识点解释物理现象,对现象进行简单分析,但分析过程会出现前后矛盾。例如对于匀速圆周运动,有些学生则会抓住“匀速”二字,从而认为匀速圆周运动是匀速运动,表明学生处在单点结构水平,这一类型的学生思维单一,不会从多角度思考问题。
对于这种学习水平的学生,在教学中可以适当地对学生进行引导,可提示学生:速度是矢量,既有大小又有方向,“匀速运动”是指速度大小和方向都不变的运动,而匀速圆周运动是曲线运动,速度大小不变,但速度方向不断改变,所以匀速圆周运动的速度是变化的。
2.3 多点结构水平
学生对待物理问题能从多个角度出发,提取相应的物理量,但不能将这些物理量整合起来解决问题,下面以一道例题为例予以说明。
例1:如图1所示,光滑圆轨道半径为R,轨道AB光滑,轨道BC水平长度为s,动摩擦因数为μ,为使小球能够通过圆轨道的最高点D,小球从AB上下滑的高度至少为多少?

图1
对于这类临界问题,学生能解决以下几个问题:(1)在AB段只有重力做功,在BC段摩擦力做负功;(2)能正确分析小球在圆周的最低点、最高点的受力情况;(3)能够用语言或者公式描述动能定理。但仅仅是简单罗列,不能将它们结合起来解决问题。
处于多点结构水平的学生能提取的知识较为零散,教师要着力于帮助学生进行知识的迁移,建立知识之间的联系,让学生的知识形成网络、融会贯通。
2.4 关联结构水平
处于该水平的学生在物理学习上主要表现为:能从物理问题中提取全部或大部分有效信息,有条理、严密地解决问题。当处于此层次水平的学生遇到上述例题时,能够给出小球恰好能够通过最高点时的速度大小,判断出小球从轨道由静止下滑到圆的最高点的过程中各力做功的情况,会应用动能定理解决问题。
教师不仅要求这类学生会做题,还应要求学生建立物理模型,以提高学生的思维水平。对于上述圆周运动临界问题,当小球通过最高点时,会出现以下两种临界状态:
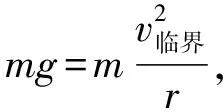

图2


图3
处于关联结构水平的学生在教师的帮助下,不仅能正确建构物理模型,还能发现单轨道模型只适用于绳拉球的情况,管道模型也可应用于杆拉或压球的情况,能举一反三,朝更高水平层次发展。
2.5 拓展抽象水平
拓展抽象水平是学生思维发展的最高层次,学生能够将复杂的实际问题转化为物理模型,能提出自己的观点。例如在上述例题中,小球在圆轨道上升或者下降时,学生就会产生疑问:既然向心力只能改变线速度的方向,那么又是什么力改变了线速度的大小呢?
学生提出的问题涉及物体在切向方向所受的合外力和切向加速度,虽然高中物理教学对这一知识点没有作要求,但是对于处在拓展抽象水平的学生,教师却可以以此为契机,引导学生更深入地理解变速圆周运动。如图4所示,当小球向上运动到圆弧的D点时,受到轨道的支持力N和重力mg,根据力的平行四边形定则,可以得到结论:合外力F合并不指向圆心。此时引导学生将F合正交分解,得到指向圆心的力F向和与圆周相切的力F切(图5),不难发现F向为向心力,F切产生了切向加速度。当F切与线速度方向相反,该力将使小球减速上升。教师还可以让学生自行分析小球沿圆弧向下的运动,从而深入理解切向加速度,解决学生内心的困惑。
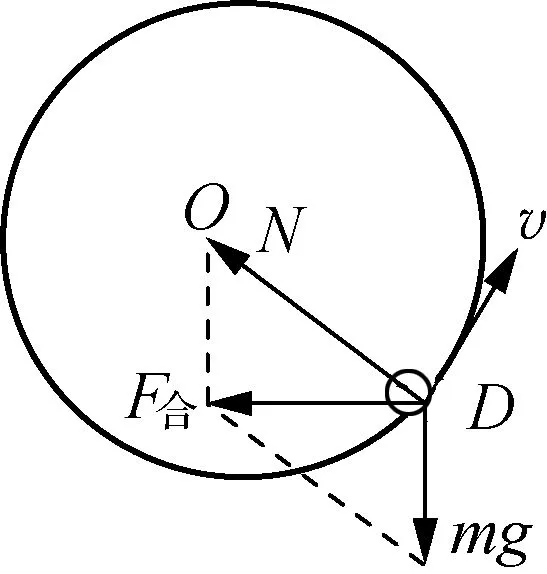
图4
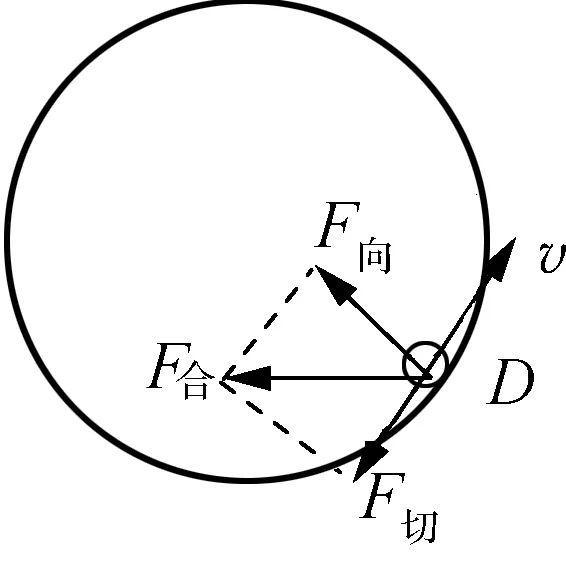
图5
处于拓展抽象水平的学生对物理学习有较大的兴趣,教师可对这些学生提出更高的要求,如参加物理竞赛。在实践操作中,将处于该水平的学生组班上课,由经验丰富、专业知识扎实的教师团队给他们上课,拓展物理教学的层次,例如在变速圆周运动的教学中向学生深入介绍切向加速度的求解及应用等。
3 结语
笔者以SOLO分类理论为指导,以“圆周运动”的复习课为例,对学生的学习水平进行了分析,并将该理论用于教学,初步的教学实践表明:将SOLO分类理论应用于高中物理复习教学是可行的。

