主控参数对中低速磁浮列车轨道响应的影响

黄良炜 刘 放

西南交通大学 成都 610031

0 引言

随着城市之间的交通状况变得愈来愈复杂，中低速磁悬浮列车因为其整体悬浮在轨道上运行，避免了因轨道接触产生的诸多问题，逐渐成为了城市轨道交通的新选择。而列车运行时的振动响应，一直是磁悬浮轨道交通的研究重点。

赵春发等[1-4]对磁悬浮车辆进行了大量的研究，分别以德国Emsland磁悬浮系统和德国Transrapid磁悬浮系统为原型，建立了磁悬浮列车的车/桥耦合动力学模型和高速磁悬浮车辆的车/轨垂向耦合的动力学模型，分别分析了当磁悬浮系统在2种支承梁结构下运行时的动力学响应特征以及磁悬浮车辆的随机振动响应。邓永权等[5]建立了磁悬浮列车的动力学仿真模型，得到了利用仿真模型可以较为准确地预测磁悬浮车辆的实际运行情况的结论。邹逸鹏等[7]将轨道高低不平顺作为外部激励输入高速磁悬浮列车的垂向动力学模型，得到了高速磁悬浮车辆垂向动力学响应。徐飞等[8]分析了中低速磁悬浮列车的运用场景。蒋海波等[10]分析了线路不平顺对磁悬浮列车动力学性能的影响，并得到了高频和低频时列车的运行状况。陆海英等[11]以电磁悬浮中低速磁悬浮系统为原型，建立了磁浮列车的耦合系统动力学模型，对中低速磁悬浮列车起浮时的振动响应特性进行了深入研究，并对电磁悬浮中低速磁浮列车运行中的失稳现象提出了解决方案。王波等[13]分析了2种不同磁轨关系对中低速磁悬浮列车动力学性能的影响，并验证了将悬浮控制模型替换为弹性阻尼模型的可行性。黎松奇等[14]对处于静态悬浮状态的磁悬浮列车进行了研究分析，并得到了车/轨的主要参数对列车垂向动力学响应的影响。

上述研究为工程实践提供了一定的帮助，但在对磁悬浮列车的动力学响应进行分析时，并未考虑到电磁场的主动控制。本文将基于中国中低速磁悬浮列车建立列车的垂向动力学模型，并引入悬浮电磁场的主动控制，仿真分析在综合考虑悬浮电磁场主动控制参数以及谐波轨道不平顺激励作为外部激励输入的情况下，中低速磁悬浮列车轨道响应的动态特性。

2 轨道不平顺激励分析

系统内部的自激振动以及外部的激扰振动是引起磁悬浮列车振动的2个主要来源。其中外部的激扰主要形式是轨道不平顺。轨道不平顺有多种类型，既包括具有随机特征的不平顺，也包括具有固定特征的局部不平顺。本文的主要研究内容为磁悬浮列车的垂向动力学性能，故采用轨道的高低不平顺作为输入激励来分析磁悬浮列车的垂向动力学性能。综合考虑局部线路不平顺的特征描述，认为其轨道高低不平顺波形可表述为规则波形。用数学公式描述，可认为其不平顺近似于正弦曲线，即

式中：A为谐波不平顺幅值，λ为谐波不平顺波长。

中低速磁悬浮列车系统对轨道线路的制造安装精度要求一般在8 mm以下，故谐波不平顺幅值取为8 mm。

3 动力学仿真模型建立

根据多体系统动力学理论，将磁悬浮列车各个部件均视为刚体，建立单节车辆的垂向动力学模型，由1个车体、5个悬浮架和20个电磁铁共26个刚体组成。动力学仿真模型三维图如图1所示，简化拓扑图如图2所示。

图1 动力学仿真模型三维图

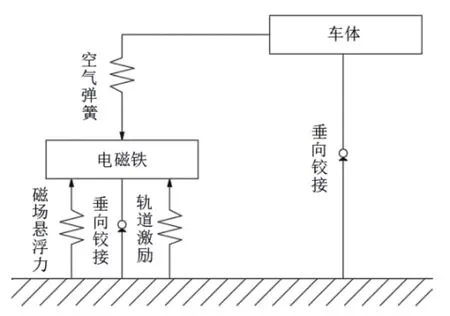
图2 简化拓扑图

单节车辆垂向模型可以简化为二自由度系统。假设各部件为刚体，得出磁浮车辆的垂向系统动力学方程为

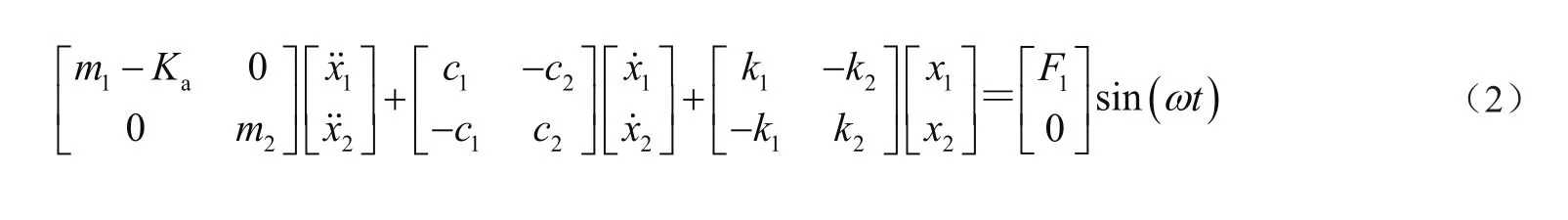
式中：m1、m2分别为电磁铁、车体的质量总和，Ka是电磁场加速度反馈系数；x1、x2分别为电磁铁、车体的垂向位移；k1、k2分别为控制悬浮电磁场、空气弹簧的垂向刚度总和；c1、c2分别为控制悬浮电磁场、空气弹簧的垂向阻尼总和；F1＝sin（ωt）为轨道高低不平顺施加到电磁铁上的激励。

4 单因素对磁浮列车动力学性能的影响

本文首先针对电磁场模型中的3个参数K、Kv、Ka对列车摇头，点头以及侧滚3个自由度角加速度的影响进行了单因素分析

4.1 K参数的影响

为了探究K参数对列车摇头、点头以及侧滚3个自由度角加速度的影响，本文中在保持控制系数Kv和Ka不变的情况下，选取3组不同的K值进行了仿真试验。其中K1～K3数值逐渐增大，截取列车运行平稳后的一段仿真结果，得到K参数分别对列车摇头、点头以及侧滚3个自由度角加速度影响的结果图，如图3～图5所示。由图可知，K对于车辆的侧滚角加速度的振动幅值有一定的抑制效果，但并未改变侧滚角加速度的振动波形。此外K对于车辆的摇头以及点头角加速度影响并不显著。

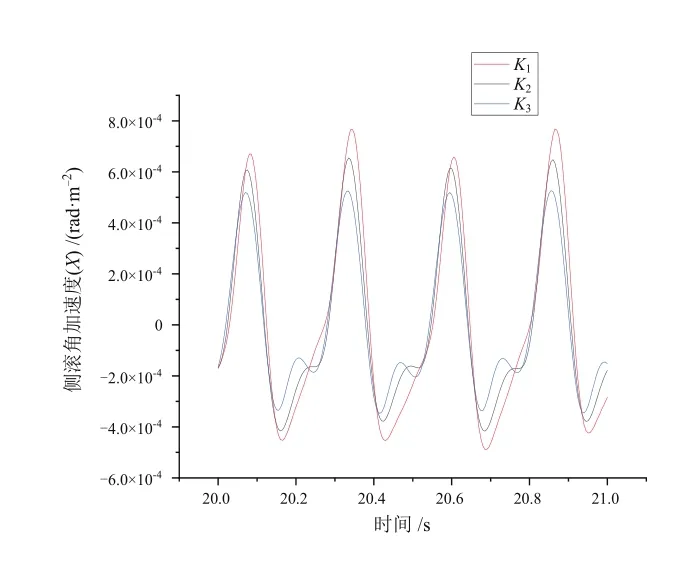
图3 K参数对侧滚角加速度的影响

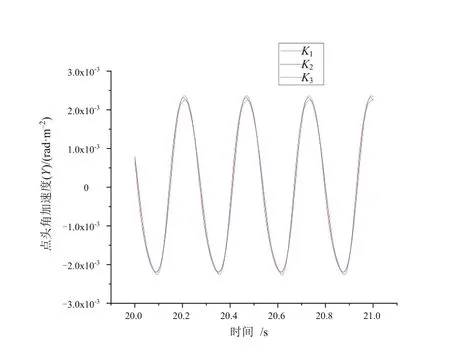
图4 K参数对点头角加速度的影响

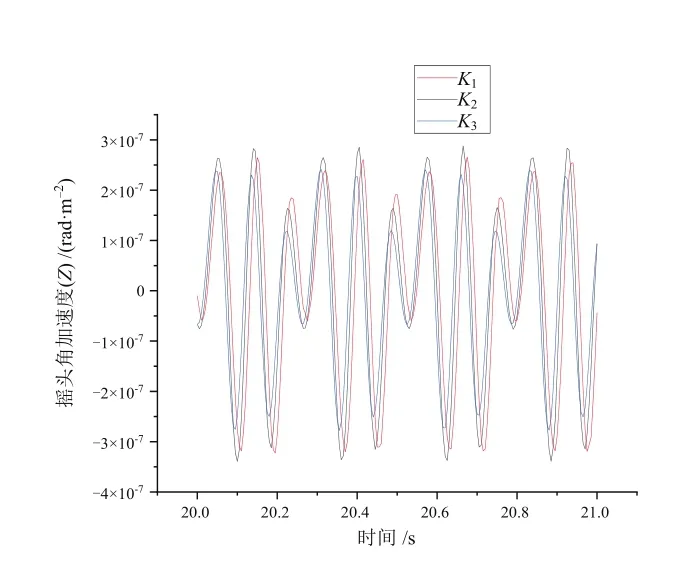
图5 K参数对摇头角加速度的影响

4.2 Kv参数的影响

与研究K参数过程相同，选取3组不同的Kv，Kv1～Kv3由0逐渐增大。仿真结果如图6～图8所示。Kv参数对于列车摇头、点头以及侧滚3个自由度角加速度影响微乎其微。

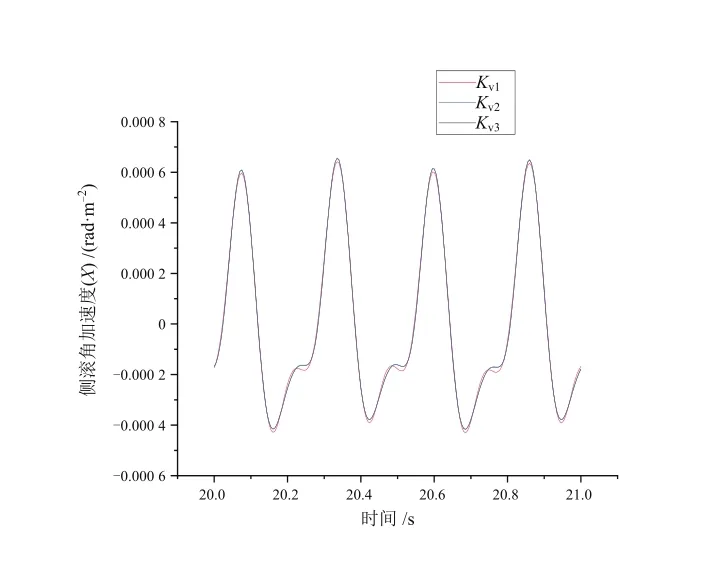
图6 Kv参数对侧滚角加速度的影响

图7 Kv参数对点头角加速度的影响

图8 Kv参数对摇头角加速度的影响

4.3 Ka参数的影响

与上述研究过程相同，选取3组不同的Ka，Ka1～Ka3由0逐渐增大，仿真结果如图9～图11所示。

图9 Ka参数对侧滚角加速度的影响

图10 Ka参数对点头角加速度的影响

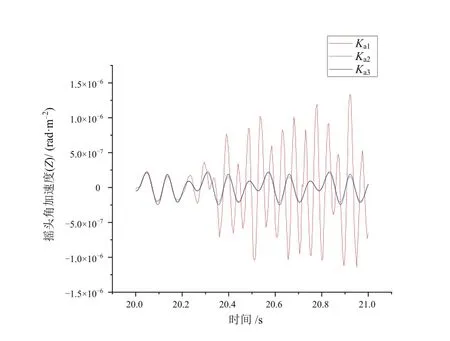
图11 Ka参数对摇头角加速度的影响

如图9和图11所示，由仿真结果可知，当Ka由0逐渐增大时，列车的侧滚角加速度和摇头角加速度的振动受抑制效果明显。如图10所示，列车的点头角加速度并不受Ka参数变化的影响。

5 多因素对磁浮列车动力学性能的影响

根据前面单因素对动力学性能的影响分析可知，Kv参数对磁浮列车摇头、点头以及侧滚3个自由度角加速度的影响微乎其微，故主要分析了K和Ka2个参数共同作用时对磁浮列车摇头、点头以及侧滚3个自由度角加速度的影响，通过仿真试验得到如图12～图14所示的仿真结果。

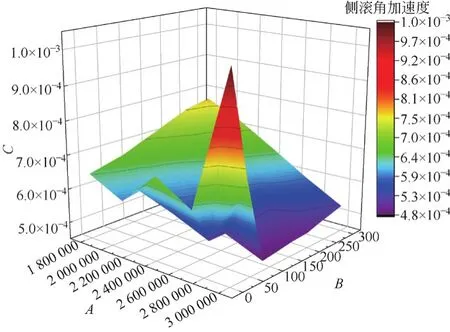
图12 K和Ka共同作用时对侧滚角加速度的影响

图13 K和Ka共同作用时对点头角加速度的影响

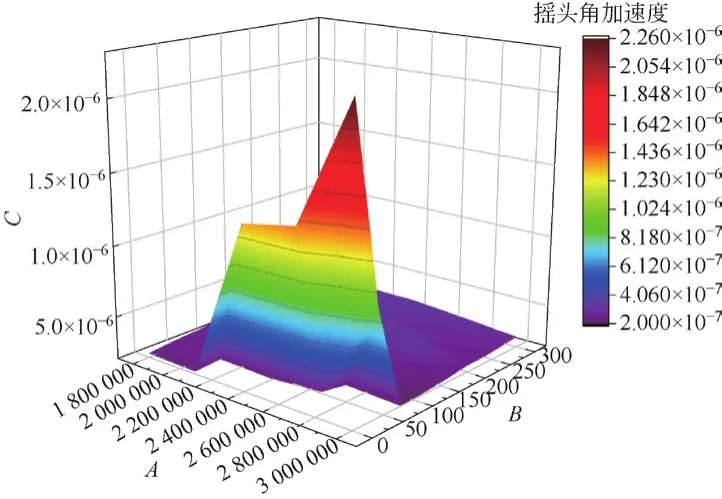
图14 K和Ka共同作用时对摇头角加速度的影响

由仿真结果可知，侧滚以及摇头角加速度峰值都出现在K最大、Ka最小的地方，而点头角加速度则正好相反；当Ka值超过一个阈值后摇头角加速度基本不会受到K和Ka参数变化的影响；对于点头角加速度，曲面呈现出两面高、中间相对低的现象；而侧滚角加速度则表现为随K的减小、Ka的增大逐渐增大的趋势。综上所述，为了得到相对较好的动力学响应，电磁场在进行主动控制的时候，使Ka值大于一个阈值的同时，K值以及Ka值均不宜过大也不宜过小，保持在适当的范围为好。

6 结论

基于Simpack多体动力学仿真软件建立了中低速磁悬浮列车的仿真模型，将轨道谐波不平顺作为外部激励输入动力学仿真模型，分析了弹性阻尼系统中3个参数K、Kv、Ka对列车摇头，点头以及侧滚3个自由度角加速度的影响，通过仿真分析得出以下结论：

1）参数K主要影响侧滚以及摇头角加速度的幅值，并未影响侧滚以及摇头角加速度的波形。对于参数Kv，3个自由度的角加速度基本不受Kv的影响。而参数Ka则主要影响侧滚以及摇头角加速度的波形。

2）参数K和参数Ka共同作用的时候，为了保证得到较好的列车动力学响应，电磁场进行主动控制的时候，参数K和参数Ka的调整应该适当，不宜过大也不宜过小。