Cutoff对FitzHugh-Nagumo方程行波解最小波速的影响

吴 琼,潘超红

(南华大学 数理学院,湖南 衡阳421001)

0 引 言

FitzHugh-Nagumo方程

f(u)=u(1-u)(u-a),a<0,

(1)

是Hodgkin-Huxley模型的简化，该方程最初由霍奇金研究尖峰沿神经传播而产生的[1]。方程(1)在物理、生物、数学、现实生活中都有很多实用的价值。其中黄建华[2]研究了在Neuman边值条件下，空间离散的方程(1)的渐近行为，并证明了在不变区域存在整体吸引子和吸引集。在此基础上，黄建华利用有限差分格式，对方程(1)同时离散时间和空间变量，获得了离散模型吸引子存在的条件[3]。石丹青[4]运用Lyapunor稳定性分析了方程(1)的稳定性，并且在非齐次边界条件下，证明了方程(1)整体解的存在性和稳定性。在现代科学技术中，为解决科学、工程科技中出现的非线性问题，余梦兰[5]应用同伦摄动理论求出了方程(1)的同伦摄动近似解。在现象学上，P.Carter[6]使用奇异摄动技术构造入侵前沿，研究了不稳定流形以及前推和后推前沿的变化，描述出相位上不稳定稳态的滑移动力学。最近，方程(1)也可用作一些行波解的优化问题，B.Karasozen和M.Uzunca[7]比较了对流FHN最优控制的适当正交分解，得出FHN最优控制的适当正交分解是最准确、最快的。对于一些特殊情况下的FitzHugh-Nagumo方程，例如带有记忆的半线性抛物方程，研究了进行错误分析的一种反馈控制技术的数值方法[8]。

FitzHugh-Nagumo方程也存在一些行波解。C.B.Tabi[9]对方程(1)的行波系统进行了定性分析，运用LS(least square)解法，CPP(catalytic pyrolysis process)解法，与李群分类法分别得到了不同种类的周期解，显式行波解[10-11]。

在诸多生物现象中，种群、密度等会出现突然地跳跃或者截断，因此考虑cutoff对方程的影响是有现实意义的[12-16]。cutoff函数是被E.Brunet and B.Derrida[12]引入来研究模型的波动，当低于某一个临界值时，会降低在区域中所有点的振幅。 在反应扩散系统中，常常引入cutoff来模拟方程行波解传播，cutoff的作用是选择一个单一的速度，该速度在ε→0时，由于截止引起的速度变化取决于完整的反应项。当将cutoff函数作用在反应项上时，这个系统的传播面的特性会发生改变。对于任何cutoff，无论多么小，都起着速度唯一选择的作用，随着cutoff的去除，行波解最小速度接近有限。 D.A.Kessler[17]考虑Refs结构稳定性，以(lnε)-2接近其波速极限值，得到选定速度对cutoff的依赖性非常显著。

本文在Brunet[12]的基础上考虑cutoff对方程FitzHugh-Nagumo行波解最小波速的影响。证明了最小波速的存在性是与ε有关，通过对三个区域行波解的光滑匹配，并进一步获得了波速改变量与ε的精确表达式。

1 主要结果

考虑cutoff在FitzHugh-Nagumo方程中对行波解最小波速的影响，因此反应项转变为

u(1-u)(u-a)Θ(u-ε)，

这里Θ(u-ε)是Heaviside阶跃函数。接下来考虑如下反应扩散方程

ut=uxx+f(u)Θ(u-ε)

(2)

经过如下变量替换

z=x-ct，u(z)=u(x-ct)=u(x,t)，

这里的c是未加cutoff的最小波速，方程(2)就变为常微分方程

u″+cu′+u(1-u)(u-a)Θ(u-ε)=0

(3)

利用Heaviside阶跃函数性质，方程(3)可以改写为

(4)

接下来通过如下三个区域来考虑方程(4)的解的渐进行为

情况一、Ⅰ区：系统(4)的第一个方程的线性方程为

u″+cu′-au=0，

(5)

并设它的解为u=e-μz。由该方程组的特征方程为

μ2-cμ-a=0，

因此方程(5)的通解为

情况二、Ⅱ区：这区间最小波速受ε的影响，假设它的最小波速为cε，因此线性化后的方程为

u″+cεu′-au=0，

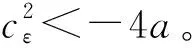
该方程特征方程的两个虚根

则线性化方程的通解为

情况三：Ⅲ区：该区域方程为

u″+cu′=0。

齐次线性微分方程的通解为u=A0e-c0(z-z0)。

接下来我们将对三个区域的行波解进行光滑匹配，因此Ⅰ区和Ⅱ区、Ⅱ区和Ⅲ区在边界处对应的函数值和导数值应该相等。

为了使得Ⅰ区和Ⅱ区的解匹配，我们获得

(6)

式(6)中两个方程作比值：

为了使得Ⅱ区和Ⅲ区的解匹配，我们获得

(7)

将式(7)中两个方程作比值得

(8)

把式(8)代入式(7)得

由

得到

其中