某工程场地剪切波速特征探讨

李义兵

(1.上海勘察设计研究院(集团)有限公司，上海 200093；2.上海环境岩土工程技术研究中心，上海 200093)

1 引言

剪切波速是结构抗震设计中的重要物理量。基于剪切波速，可对场地土类型进行定量划界、评价土体的液化性能、定量计算土工地震反应[1～3]。

本文基于某工程的地质特征，分析了剪切波速测试结果的基本特征，为地震评价提供基本依据。

2 工程地质特征

某工程位于镇江市，包括多栋多层及高层住宅，高层建筑采用剪力墙结构。根据勘察报告，场地土自上而下包括：①素填土；②1粉质粘土;②2粉质粘土;③1粉质粘土;③2粉质粘土;③3粉质粘土;④含碎石粉质粘土;⑤1全风化火成岩;⑤2强风化火成岩;⑤3中风化火成岩，具体特征见表1。典型工程地质剖面如图1所示。

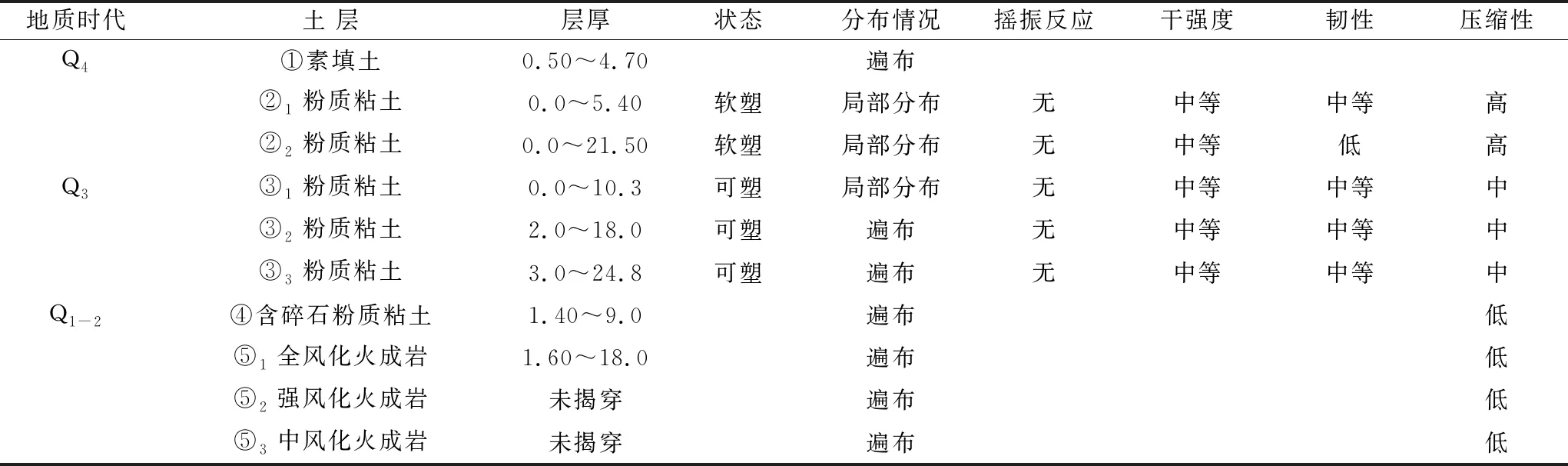
表1 各土层特征描述

表1中，⑤1全风化火成岩、⑤2强风化火成岩、⑤3中风化火成岩，主要矿物成分有石英、长石及长石风化物、少量云母及闪长石等，岩体基本质量等级Ⅴ～Ⅳ级。

3 剪切波速测试成果

按照相关规程，本次共完成22 个孔的波速测试工作，完成测试孔工作量及技术参数如表2所示。部分钻孔的剪切波速与深度关系如图2与图3所示，所有钻孔的剪切波速数据如图4所示。

基于剪切波速测试数据，可反算得到各土层的剪切波速平均值，见表3。本场地覆盖层厚度<50 m，根据建筑抗震设计规范[1]，单孔场地类别判定结果如表4所示。

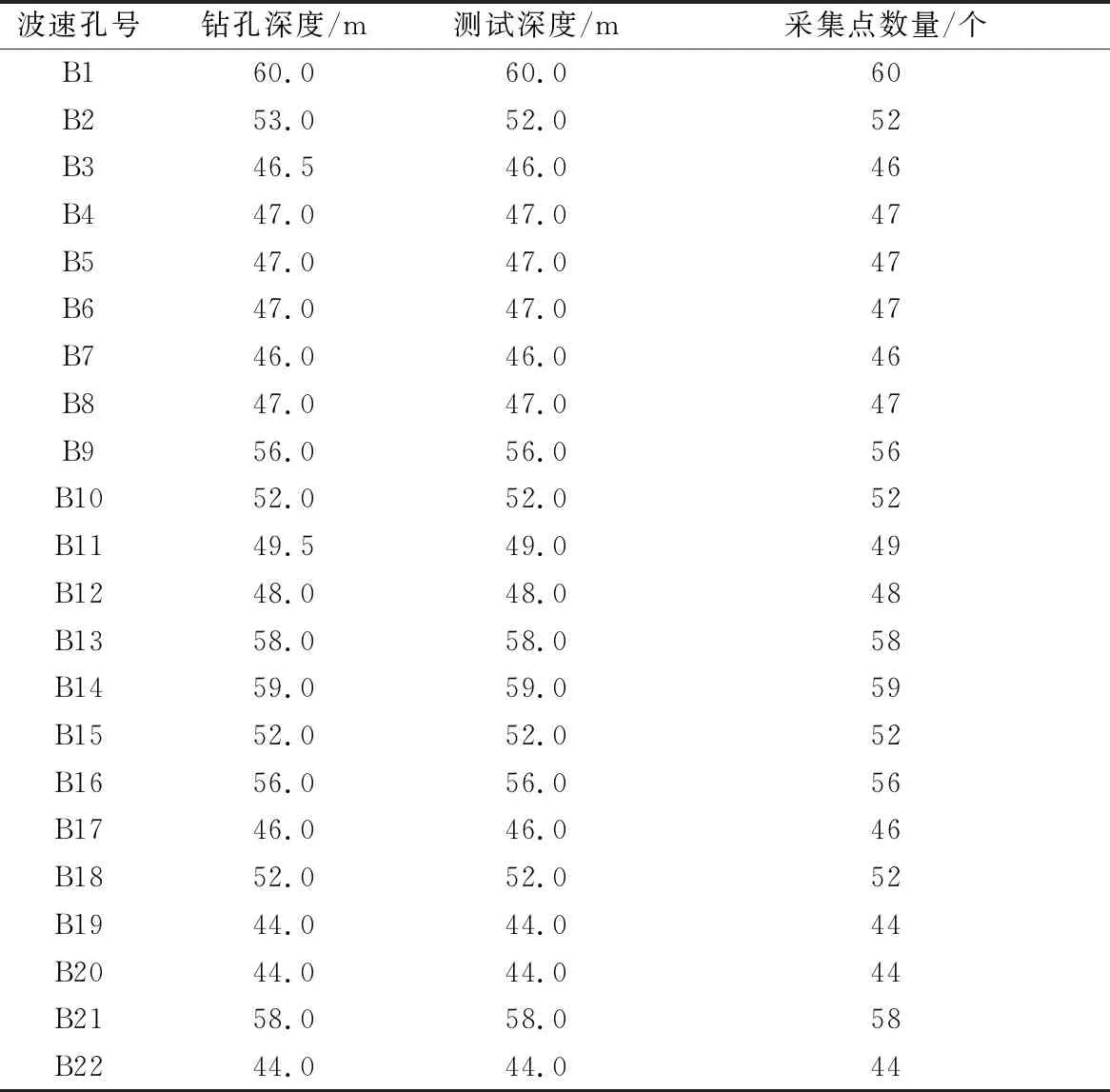
表2 波速测试孔技术参数

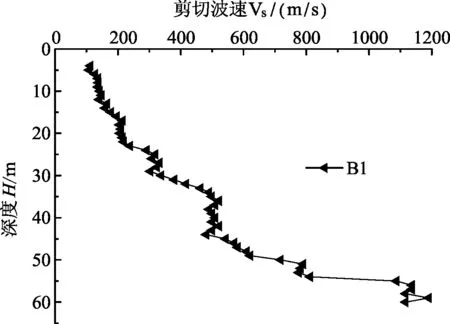
图2 B1孔波速测试成果

图3 B21孔波速测试成果

图4 所有测孔数据分布

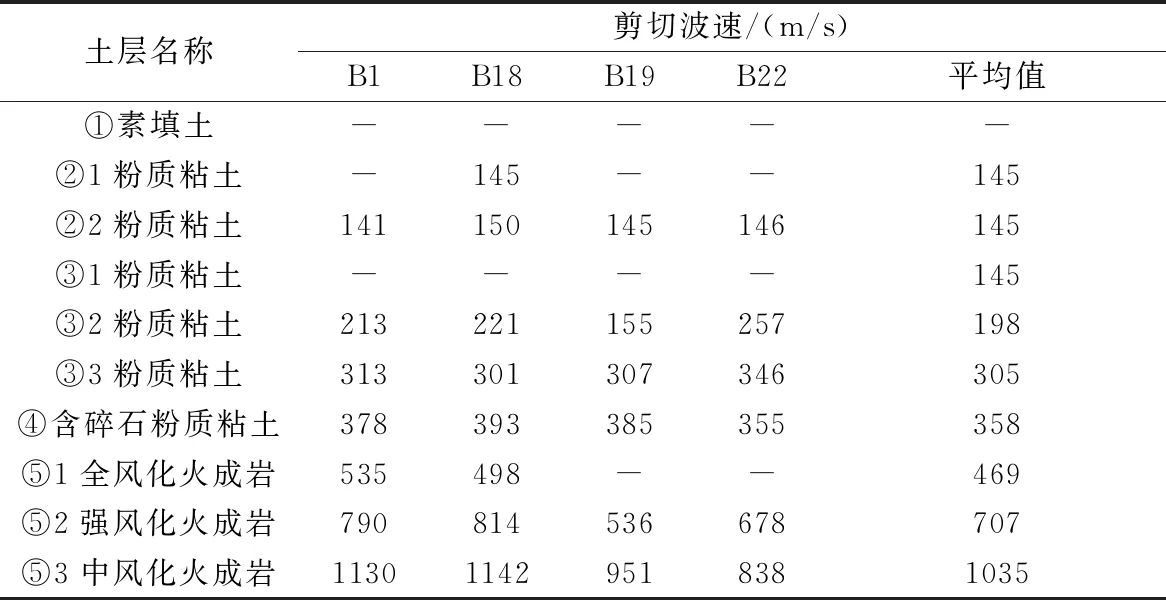
表3 各土层剪切波速一览

4 剪切波速与深度关系

一般地，可采用下列3种常见模型对土层剪切波速与埋深之间的关系进行数学回归拟合[4～9]：

线性函数模型：Vs=aH+b

(1)

一元二次函数模型：Vs=cH2+dH+f

(2)

幂函数模型：Vs=gHi

(3)

基于各土层剪切波速测试数据，通过数学拟合得到三种模型的反演参数，见表5所示。其中R2表示校正决定系数，可反映总体回归效果的优劣。各土层剪切波速Vs与深度H的相互关系如图5～10所示。

可见，对于工程所在场地的③1粉质粘土、⑤1全风化火成岩来说，采用幂函数模型模拟剪切波速与深度相互关系的精度较高；对于③2粉质粘土、③3粉质粘土、⑤2强风化火成岩、⑤3中风化火成岩来说，采用一元二次函数模型模拟剪切波速与深度关系的精度较高。这些规律对同地区场地剪切波速的预测具有一定的指导意义。

表5 各土层剪切波速一览

图5 ③1粉质黏土剪切波速与深度关系

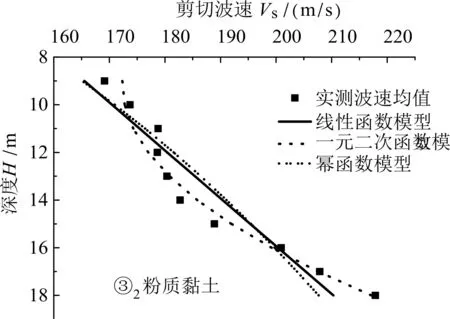
图6 ③2粉质黏土剪切波速与深度关系

5 结语

以镇江市某工程场地为例，在分析工程地质特征的基础上，对各土层剪切波速的实测值进行了分析，获得了抗震中的场地类别。并基于常见的三种函数模型对各土层剪切波速与深度的关系进行了数学回归拟合，结果表明所在场地的③1粉质粘土、⑤1全风化火成岩采用幂函数模型模拟剪切波速与深度关系的精度较高；对于③2粉质粘土、③3粉质粘土、⑤2强风化火成岩、⑤3中风化火成岩采用一元二次函数模型模拟剪切波速与深度关系的精度较高。这些规律对同地区场地剪切波速的预测具有一定的指导意义。

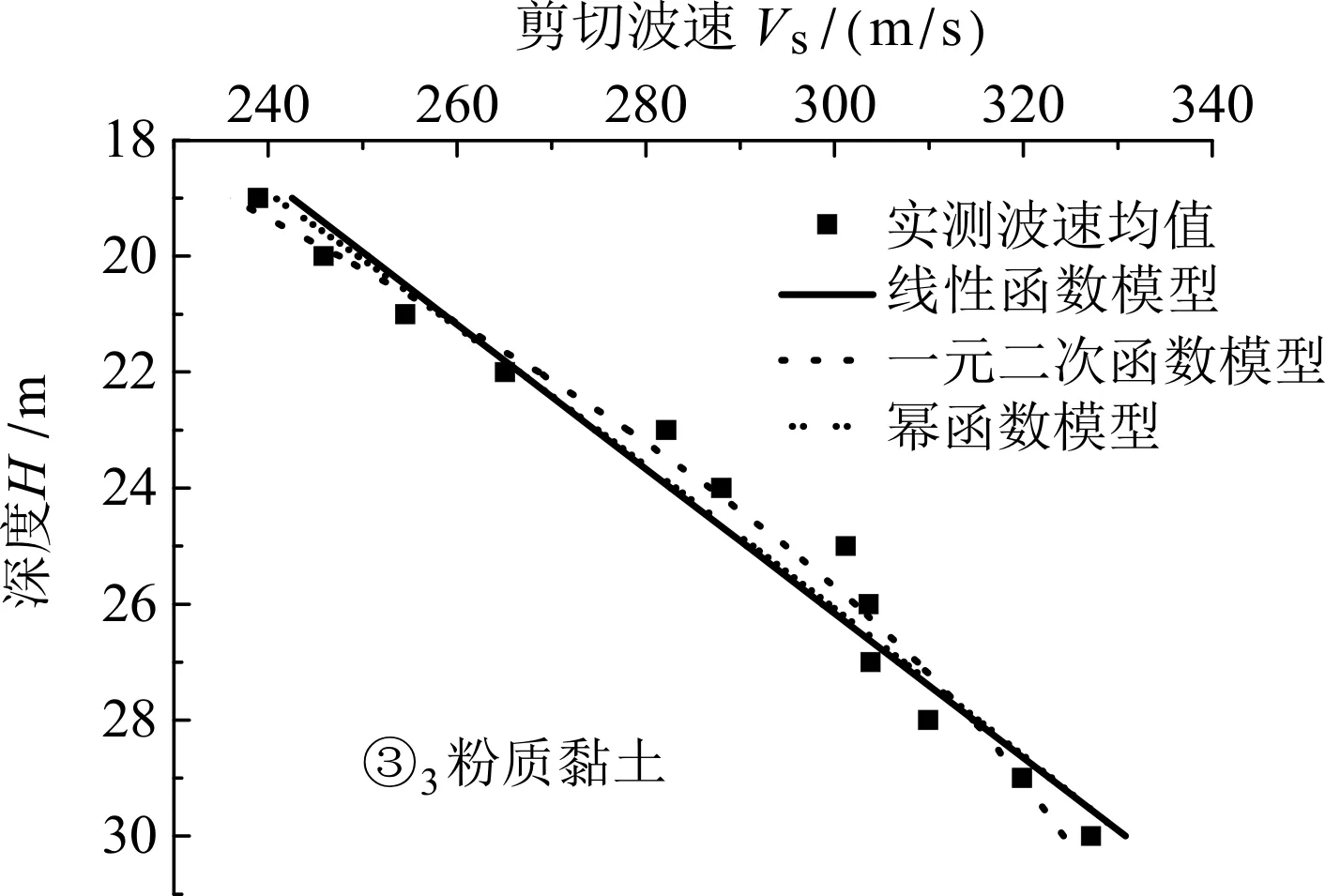
图7 ③3粉质黏土剪切波速与深度关系

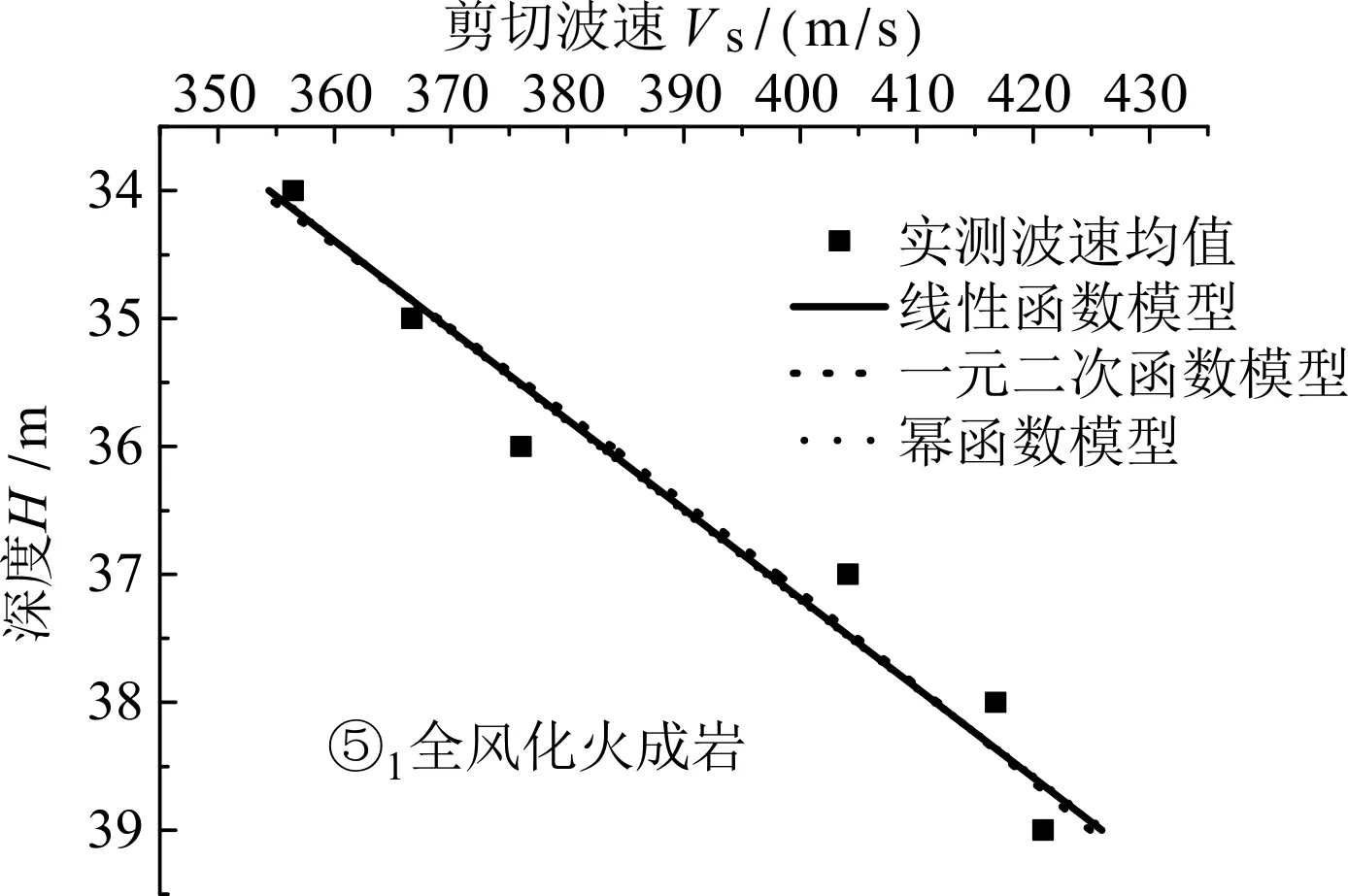
图8 ⑤1全风化火成岩剪切波速与深度关系

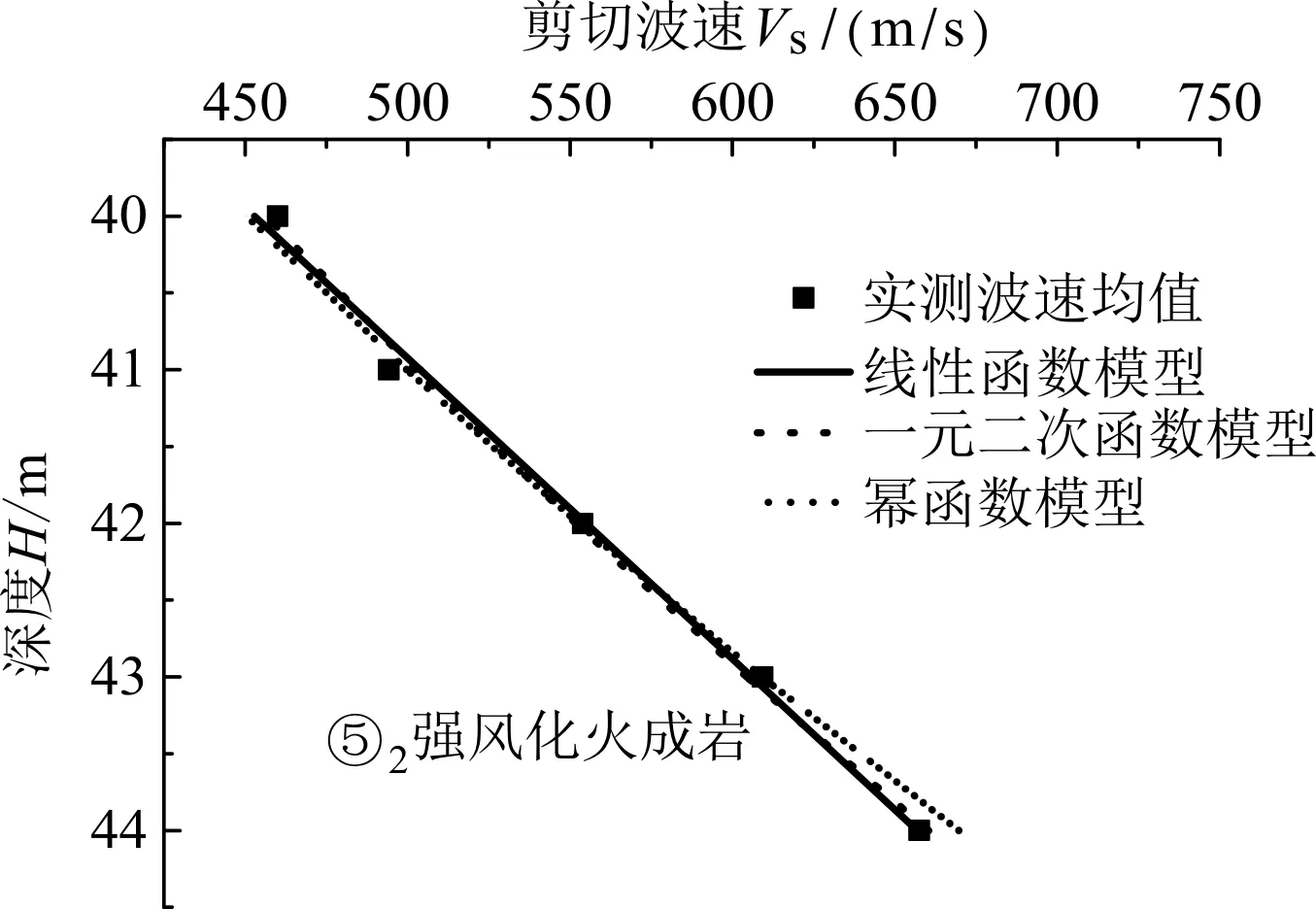
图9 ⑤2强风化火成岩剪切波速与深度关系

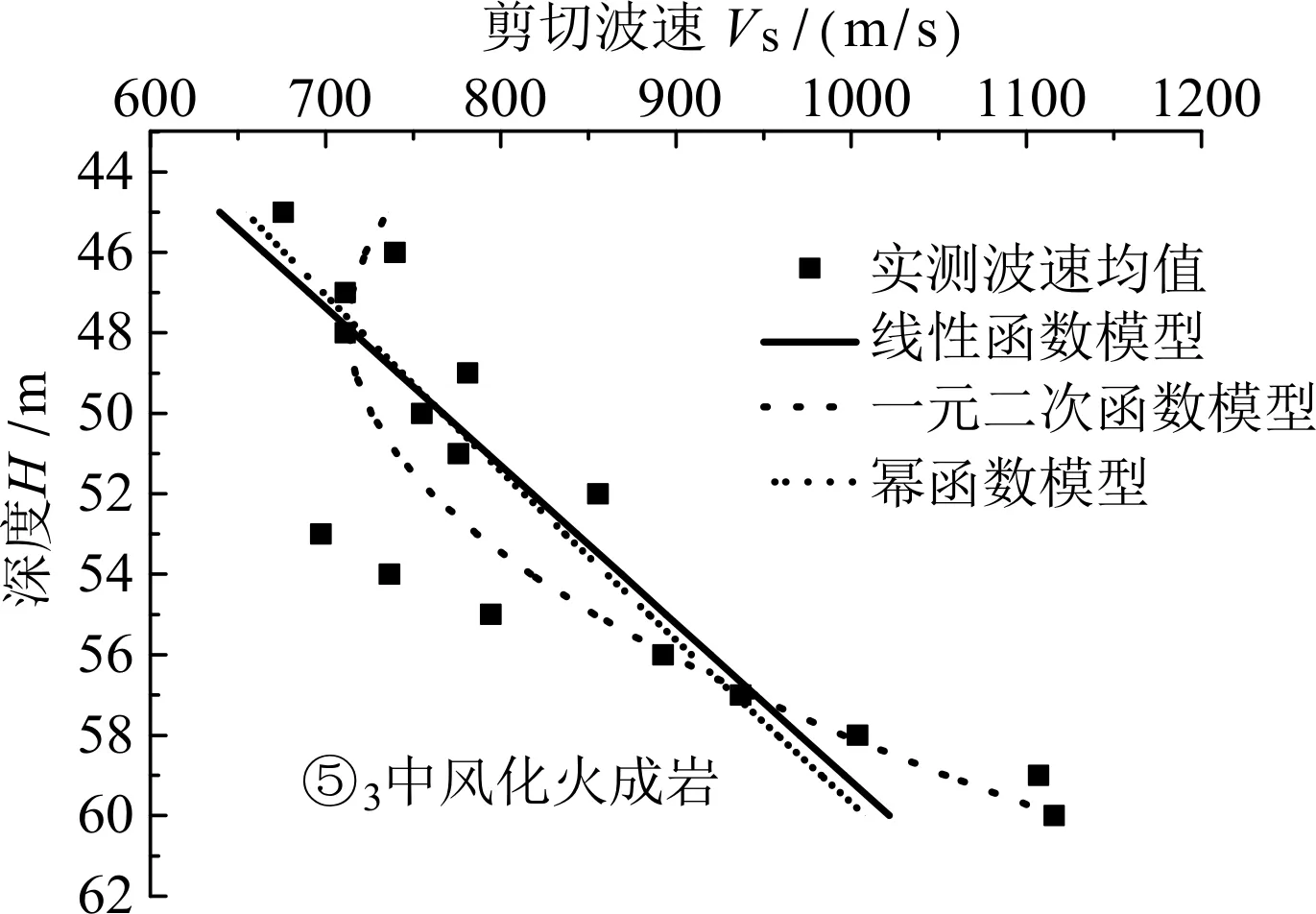
图10 ⑤3中风化火成岩剪切波速与深度关系