关联交叉口延误计算模型研究
刘庆广,顾玉牧,林培群
(1. 江苏航运职业技术学院 运输管理与经济学院, 江苏 南通 226010;2. 华南理工大学 土木与交通学院,广东 广州 510640)
0 引 言
交叉口评价指标是衡量交叉口运行情况的重要依据[1]。很多学者都对交叉口评价指标进行了深入研究,尤其是对单个交叉口延误及排队长度的研究相对比较成熟[2-3]。单交叉口的研究一般对交通流运行情况进行了适当的简化,假设交通流始终按照固定的速率驶入对应车道,但对于关联交叉口,实际交通流到达情况是由上游交叉口配时方案所决定的。例如,随着关联交叉口(周期相同)相位差的改变,车道对应的延误、排队长度等也相应变化:当采取绿波协调控制时,延误和排队长度将显著下降,而传统的交通模型无法体现这一过程。因此,部分学者开始研究关联交叉口的评价指标求算。王进等[4]、姚荣涵等[5]以交通波理论为基础,建立了同周期相邻交叉口的最大排队长度模型,同时提出了“时空协调指数”的概念,分析了时空协调指数与路段流量、路段长度、配时方案、最大排队长度等多元关系;王进等[6]基于交通波理论,建立了考虑上游信控方式的延误模型。但是,利用交通波理论建立排队长度模型和延误模型存在一定缺陷;S. B.KERNER[7]通过大量数据统计提出了三相交通理论,当交通流量超过一定阈值时,速度与密度呈现出离散的状态,此时,传统交通波理论不再适用;杨少辉等[8]、曲昭伟等[9]、姚荣涵等[10]提出,传统交通波理论采用格林希尔治速度-密度模型,这与实际观测数据存在一定偏差,需要大量数据进行分析矫正。笔者选择传统稳态交通理论为基础,建立关联交叉口“相位差-延误”模型,求解过程清晰简明。同时,可有效避免交通波理论存在的问题对延误计算的影响。
1 基本原理
相位差-延误计算模型基于经典Webster延误模型,考虑对象为关联交叉口,其特点是周期相同,存在相位差。因此,下游交叉口进口道的交通流实际上是周期性地按照上游交叉口各相位依次放行到达,所以,延误计算应该包含相位差这个参数。该模型有别于传统的延误计算模型,一定程度上可以解决传统延误模型无法随相位差变化,相应计算关联交叉口进口道延误的缺陷。
记Tm(tm,Nm)为排队车辆的时空点位坐标。其中,tm为当前时刻,Nm为排队车辆数。如图1,关联交叉口的车流并非按照相同流率驶向下游,而是绿灯启亮后,先按照饱和流率驶向下游;当排队车辆完全消散后,按照当前相位流率驶向下游。
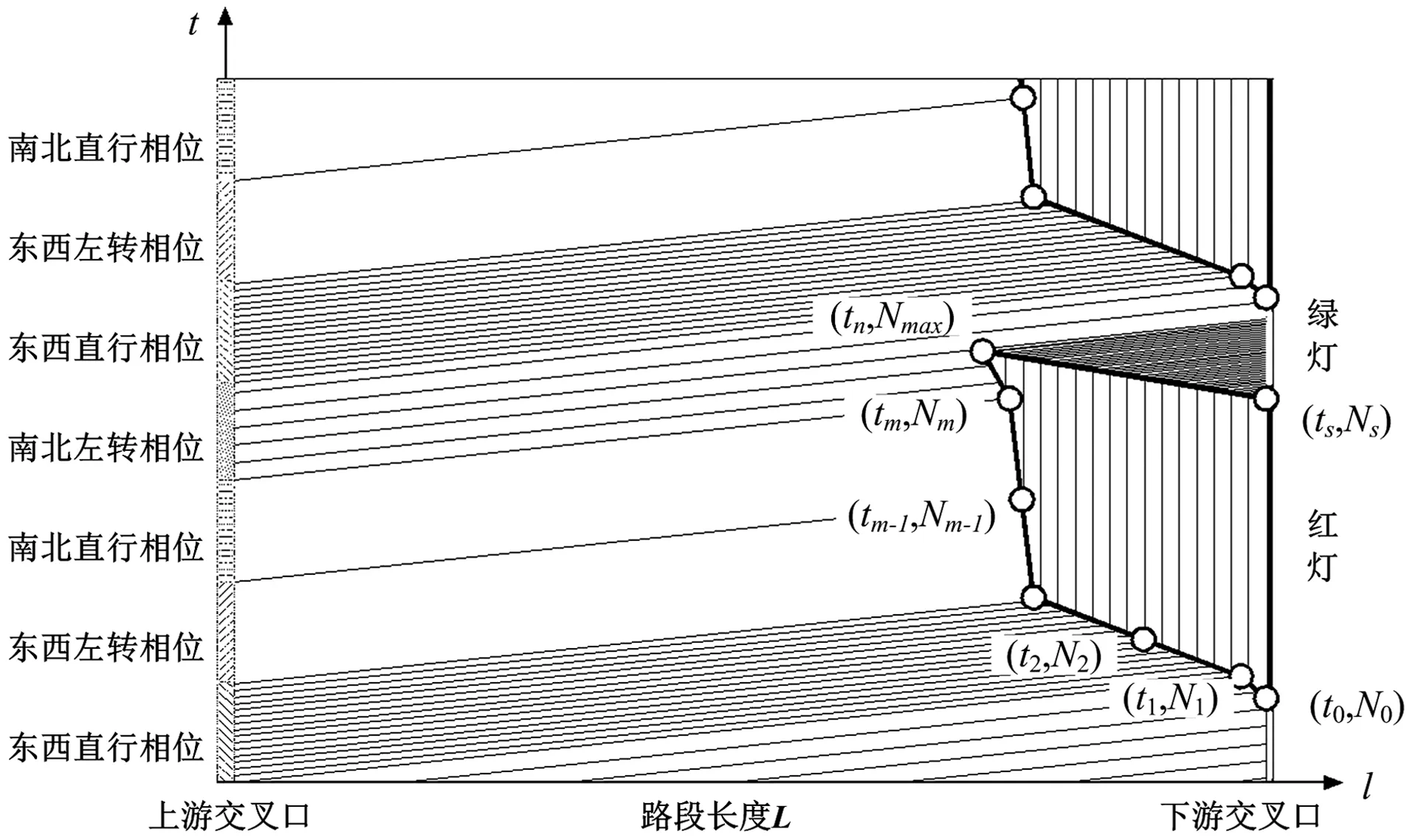
图1 关联交叉口车辆排队演化过程
以图1为例,上游交叉口与下游相关联的流向组(东西直行+南右转、南北左转+南右转)按照不同的交通流率驶向下游西进口;与下游无关联的相位(东西左转、南北直行)则按照不受信号灯控制流向组车流(南右转)的流率驶向下游交叉口西进口。
类比传统交通稳态理论可知,一组空心圆圈连线(t0,N0)→(t1,N1)→(t2,N2)→…→(tm-1,Nm-1)→(tm,Nm)→…→(tn,Nmax)→(ts,Ns)与下游交叉口纵轴围合成的多边形面积即为一个周期内的总延误。
2 计算模型推演
2.1 分阶段流率计算
如图2,上方坐标轴表示上游交叉口车流按照相序分阶段不同流率驶向下游交叉口;下方坐标轴表示下游交叉口按照上游交叉口分阶段流率达到以及自身相位放行形成到达-消散过程。其中,θi是0-1变量,当前车流驶向下游交叉口时定为1;η为下游对应车道流量占总流量比重;qi为上游第i个流向流率;tRi为红灯时长;Si为当前放行的受控流向饱和流率;tGi为绿灯时长;qJ为不受控流向流率。
根据Webster公式可知,计算排队车辆完全消散时长tSi:
(1)
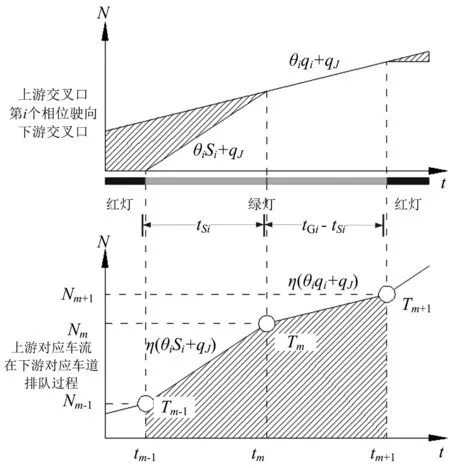
图2 绿灯时间内下游交叉口车辆排队过程
因此,上游交叉口第i个相位绿灯时长内驶向下游交叉口的车流分两个阶段,按照不同速率驶向下游:①tSi时长内车道车辆以θiSi+qJ流率驶出;②(tGi-tSi)时长内车道车辆以θiqi+qJ流率驶出。
综上,上游交叉口按照不同相位分时段驶向下游交叉口的流率如图3。
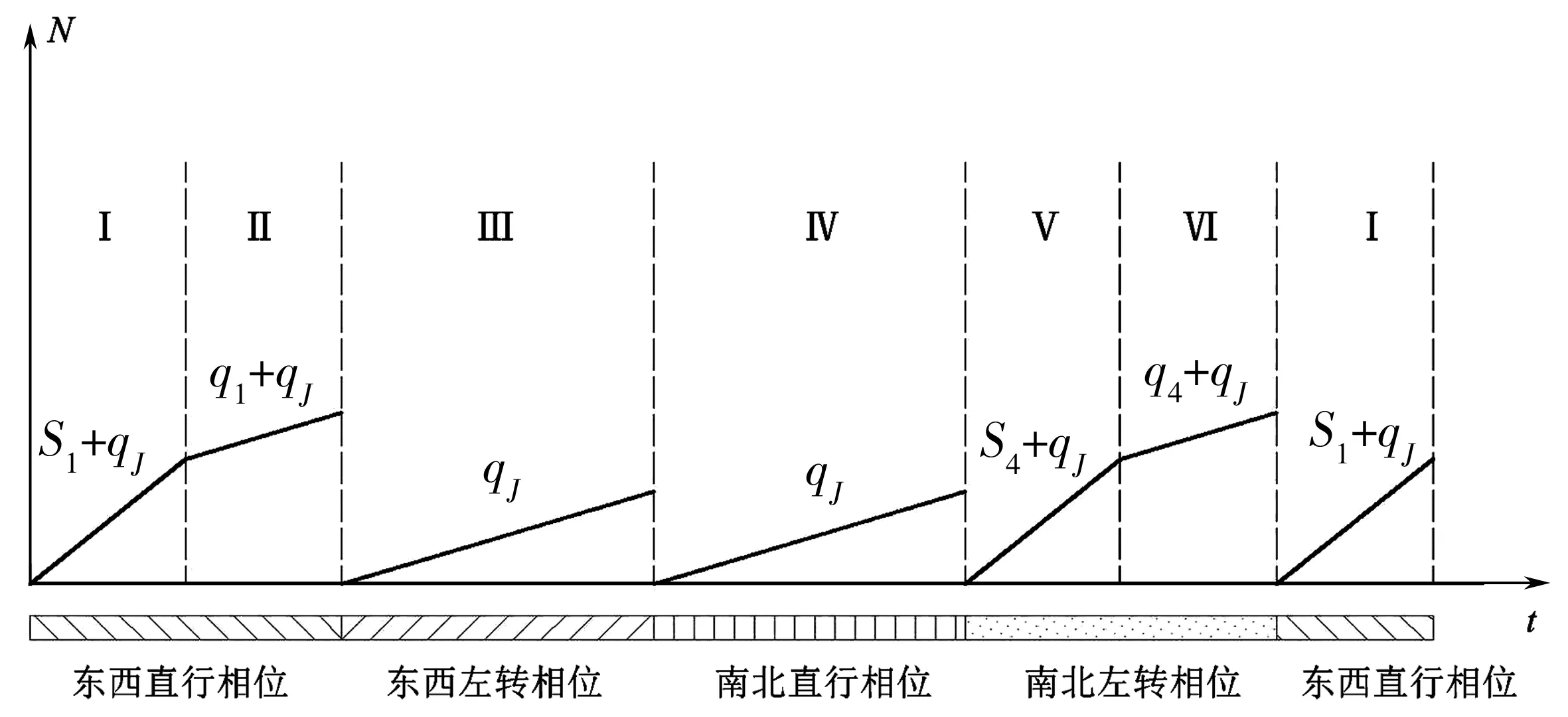
图3 上游交叉口车流分阶段驶向下游交叉口过程
即图1中围合区域时空空心圆圈中(t0,N0)→(t1,N1)→…→(tn-1,Nn-1)均可通过图2和图3的推算获得。
2.2 最大排队车辆数计算
如图4,计算图1中完全消散点位(tn,Nmax)。
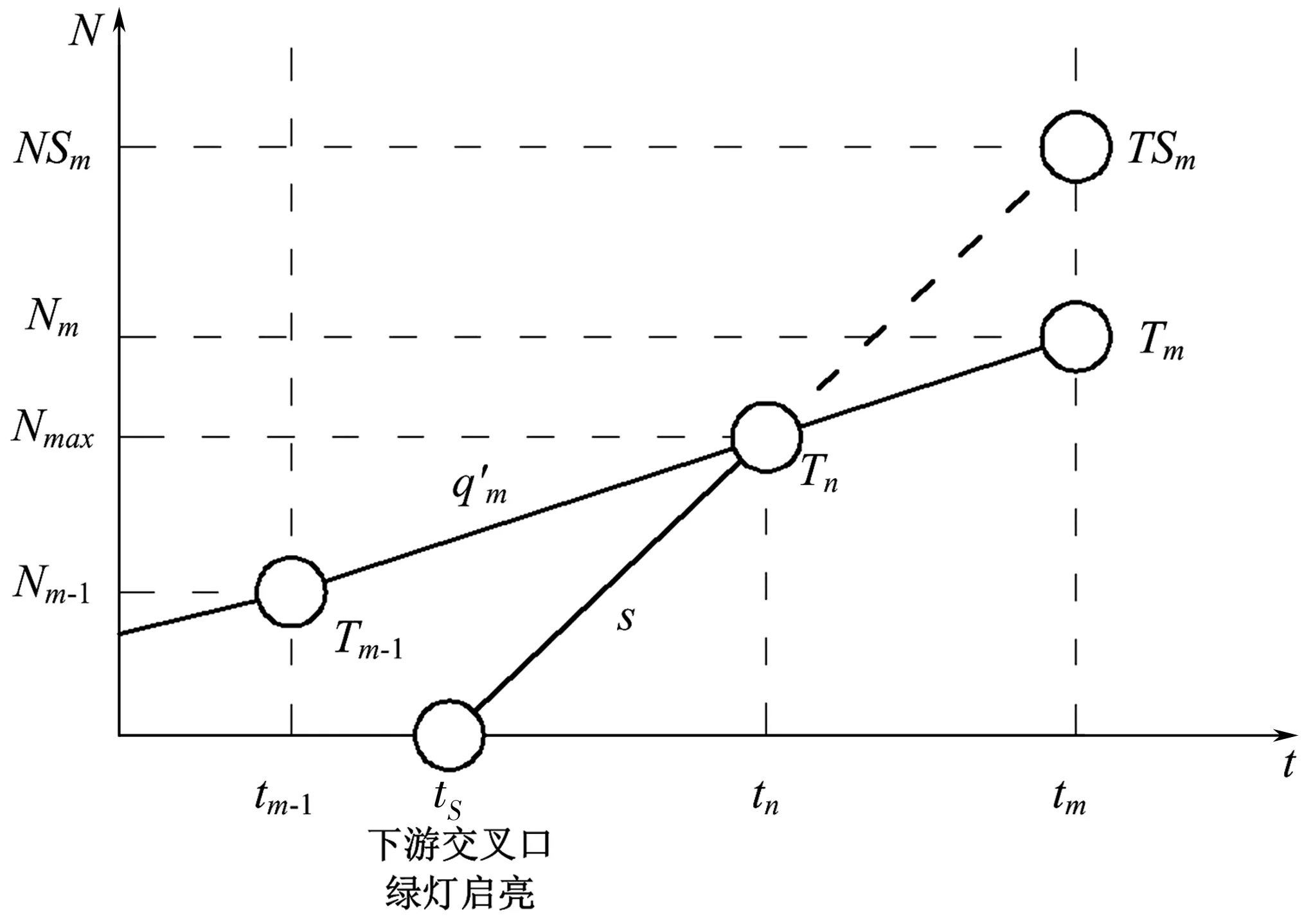
图4 最大排队车辆数计算示意
图4中,到达流率q′m是不断变化的,q′m=η(θiSi+qJ)或q′m=η(θiqi+qJ)。因此,需要逐步演化当前状态,来计算最大排队长度。具体计算过程如下:
步骤1:当前时间区域内排队车辆是否完全消散。计算方法如式(2):
(2)
若NSm 步骤2:此时NSm≥Nm,排队车辆完全消散。计算当前最大排队车辆数。首先求解到达函数和消散函数的交点,如式(3): Nm-1+q′m·(tn-tm-1)=S·(tn-tS) (3) 求解式(3)得式(4): (4) 步骤3:求解对应最大排队车辆数Nmax=S· (tn-tS)。 图1中围合区域面积与一个周期内车辆到达数的比值,即为关联交叉口的平均延误。计算公式如式(5): (5) 式中:qC为一个周期内计算车道(组)的到达流量。 利用交通微观仿真软件VISSIM验证模型,比对仿真结果与模型计算结果,如图5。VISSIM仿真参数设置如表1。 两相邻交叉口停止线间距离为400 m;饱和流率约为1 625 pcu/h(通过在停止线上设置车辆检测器,测多组饱和流率取均值);相位差数值以5 s为间隔,即相位差分别取0,5,10,…,120 s。 图5 VISSIM仿真交叉口 表1 VISSIM仿真各参数设置 相邻交叉口流量及其配时方案如图6、图7。图7 中,共同周期为120 s,黄灯3 s。 图6 关联交叉口流量 图7 关联交叉口配时方案 为了清晰的解释相位差-延误模型,笔者以下游交叉口西进口直行车道红灯启亮时刻处于80 s为例计算下游交叉口Ⅱ东进口直行车道平均延误。 3.2.1 时间区域及对应流率计算 根据式(1)可知,图3中时间区域Ⅰ和Ⅱ时间长度分别为: tⅡ=tG1-tS=60-36=24 s 直行车道车流占总进口道比例为: η=450/(300+450+150)=0.5 因此,对应阶段的交通流率为: QⅠ=0.5×(1 625+200)=912.5 pcu/h QⅡ=0.5×(600+200)=400.0 pcu/h 以此类推,可以获得上游交叉口时间分区,如表2。 表2 上游交叉口阶段划分及对应流量 3.2.2 车辆排队时空点(红灯)的演化计算 t0=78 N0=0 t1=80 N1=N0+ηqJ·(t1-t0)= 0+0.5×(200/3 600)×2=0.56 t2=110 N2=N1+ηqJ·(t2-t1)= 0.56+0.5×(200/3 600)×30=0.89 t3=118 N3=N2+η(S+qJ)·(t3-t2)= 0.89+0.5×[(1 625+200)/3 600]×8=2.92 t4=120 N4=N3+η(q4+qJ)(t4-t3)= 2.92+0.5×[(100+200)/3 600]×2=3.00 3.2.3 车辆排队时空点(绿灯)的演化计算 根据2.2节的公式计算绿灯亮起后的车辆排队消散直至绿灯结束的时空坐标。 综上,红灯期间排队过程和绿灯期间消散过程如图8。 图8 下游交叉口时空演化 3.2.4 平均延误计算 根据式(5)计算关联交叉口平均延误值: Nmax·(tn-tS)/2=496.95 s 此时VISSIM仿真结果为33.40 s,结果较为吻合。 3.2.5 交通仿真与模型计算比较 按照3.2.1~3.2.4节方法推演不同相位差下的结果,仿真间隔选择5 s,比较交通仿真与模型计算结果,验证相位差-延误模型的可行性和有效性。具体结果如图9。 图9 交通仿真与相位差-延误模型延误结果比对 如图9,直行车道延误平均相对误差为4.64%,平均绝对误差值为1.4 s;左转车道延误平均相对误差为3.25%,平均绝对误差值为1.8 s。利用交通波理论推演关联交叉口平均相对误差值一般在6.0%左右[6]。笔者方案推演结果更加接近交通仿真结果。主要原因是交通波理论需要根据实际情况选择合适的公式修正,而交通稳态理论模型相对简明清晰,便于计算。 此外,通过对比可以发现,在峰值上延误的偏差较大,这主要是由于当相位差设置极为不合理时,车道会出现排队过长等情况,车辆运行行为更加复杂,使得仿真延误值会比计算值略大一些。 通过分析关联交叉口之间的交通流运行特点,创造性地将相位差等参数引入到关联交叉口延误计算模型中,动态反映关联交叉口的信号方案、流量流向等对延误的影响,弥补了Webster延误模型在关联交叉口延误计算上的不足。模型的计算值与VISSIM仿真结果较为接近,可定量分析关联交叉口运行的延误情况。后续将对模型峰值延误比仿真峰值延误低等问题进行更加深入的研究。2.3 计算关联交叉口平均延误
3 关联交叉口相位差-延误模型验证及分析
3.1 仿真建模
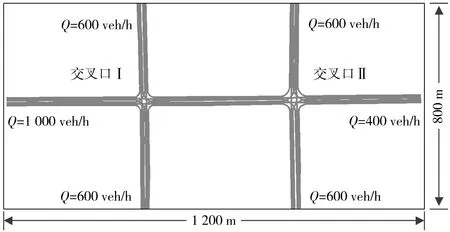


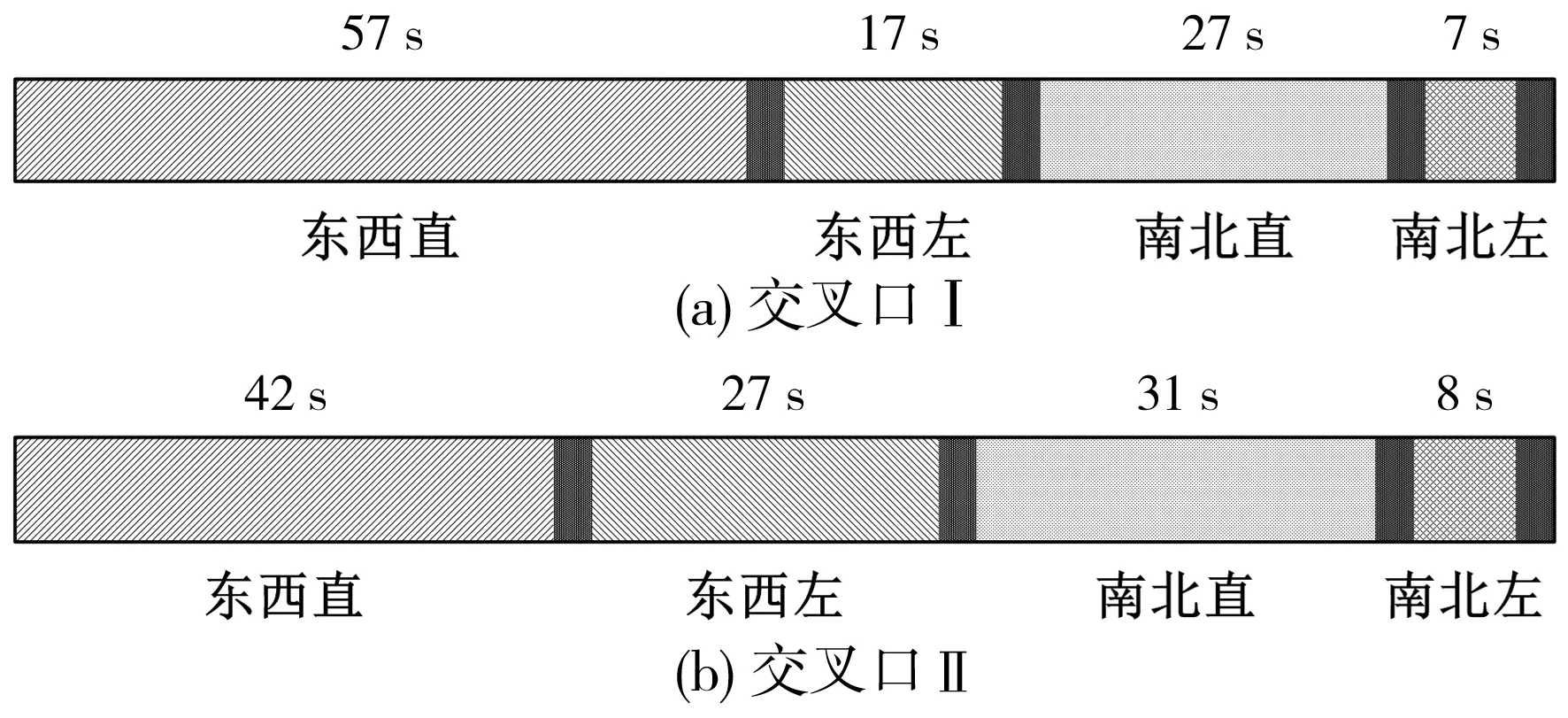
3.2 相位差-延误计算模型计算

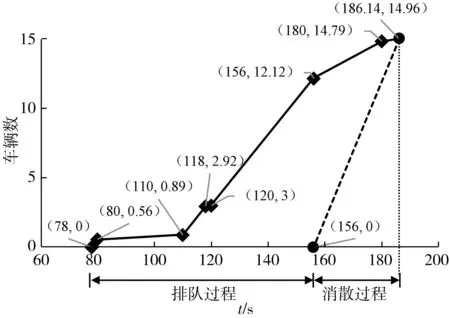
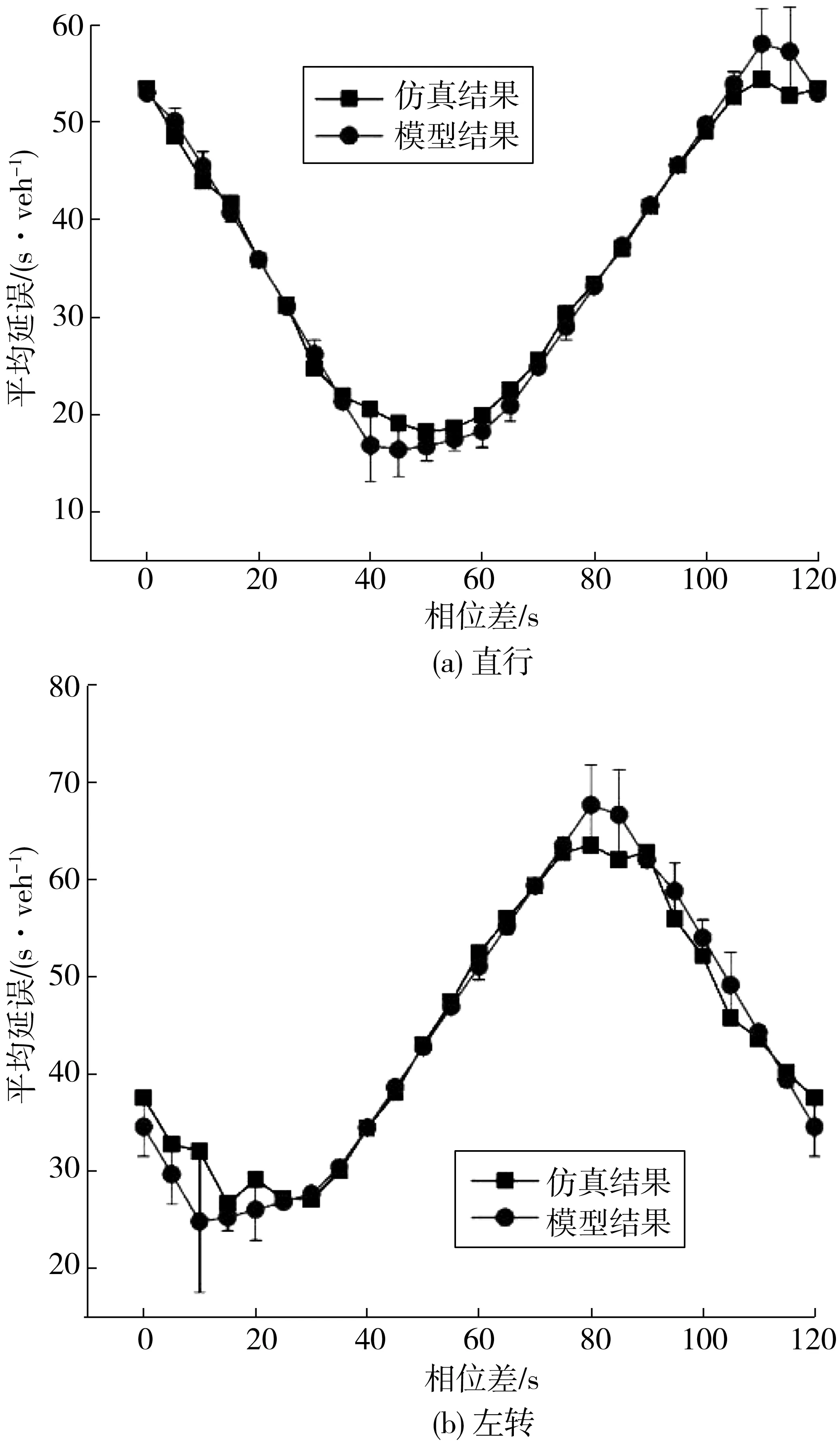
4 结 语

