城市轨道交通快慢车方案线路通过能力研究

王晓潮，周 鲁，金 华，田 梦

(1. 广州地铁设计研究院股份有限公司，广东 广州 510010；2. 北京交通大学 交通运输部综合交通运输大数据应用技术交通运输行业重点实验室，北京 100044)

0 引 言

快慢车技术是通过加开在部分客流较少的中间站不停车快速列车，以此解决长距离出行的速度问题，同时兼顾客流可达性的一种方法。该方法解决了运营中客流在空间上不均衡分布带来的车站负荷不均衡问题，是实现均衡车站负荷的重要技术之一，适用于具备越行条件的线路[1]。对于车站负荷不均衡线路，采用站站停运营组织模式会造成列车旅行速度偏低、长距离出行时间增加等问题，会阻碍运营综合效益提高。例如：西安地铁2号线钟楼站、会展中心站、小寨站客流集散量约占全线的42%；广州地铁5号线珠江新城、五羊邨、滘口、小北和广州火车站集散客流占全线客流的39%[2]。

快慢车运营组织虽可减少长距离出行时间，同时兼顾客流可达性，但会增加运营组织复杂程度，并因采用非平行运行图而影响线路通过能力[3-4]。这种因非平行运行图造成的能力损失是对快慢车运营组织的重要评价指标之一[5]。故有必要对快慢车方案线路通过能力进行深入分析。

针对快慢车通过能力的研究主要可分为两大类：① 通过绘制运行图以获得线路通过能力，例如：赵欣苗等[6]、和扬[7]、黄林尧[8]、姚赛君[9]，这些学者通过建立运行图模型，在给定条件下通过算法求解获得运行图，从而获得线路通过能力；② 通过对问题进行抽象后，采用经验公式对线路通过能力进行计算，例如：赵源等[10]、张乾睿等[11]、魏玉光等[12]、张泽英等[13]。第1类方法可获得运行图，据此计算准确的通过能力，但需建立复杂模型；而采用经验公式计算更适用于规划阶段分析。但采用经验公式存在其普适性较差现象，关键参数难以直接获得。例如：文献[10]以发生越行的快慢车在始发站间隔作为参数进行通过能力计算；文献[11]则通过重复出现的最小快慢车-车组合周期进行通过能力计算；文献[12]提出了将停站作业虚拟为闭塞区间新方法，但同样在计算中使用了快车发车间隔和被越行慢车数等参数。此外，文献[13]粗略计算了通过能力，仅考虑了一次越行情况。

关键参数的确定过程通常会对通过能力计算带来不便。笔者采用越行站最小到-到、发-发间隔、最小追踪间隔及快慢车停站方案等易得参数对快慢车方案下线路通过能力进行计算；并结合实例，对越行站数量及位置对快慢车方案下线路通过能力进行分析。

1 前提假设

笔者针对快慢车方案下线路通过能力的计算模型做出以下假设：

1)仅存在车站越行；

2)快车每不停站通过1个站，相比慢车节约固定时间t节约，其值为停站时间加起停附加时分；

3)慢车最多被两列快车越行；

4)快慢车列车型号一致，仅停站方案不同；

5)列车区间运行时间为定值；

6)快慢车比例仅考虑1∶1、 1∶2、 2∶1等。

假设1)考虑到城市轨道交通多为地下线路，且站间距较短，多为双线，而区间越行需有3线或4线区段，多见于区域轨道交通和国家干线铁路[14]，因此只考虑车站越行；假设2)基于文献[15]，在对相同速度等级列车因停站产生的速度差异进行研究，指出对于列车类型相同的快、慢车而言，时间差异主要由停站时间及制动和启动时间差异造成，并给出了如假设2)结论；假设3)考虑到快慢车模式下在发车密集时，会出现快车越行慢车的情形[16]，然而由于城市轨道交通线路较短，且越行站待避会大大降低慢车旅行速度[17]，故实践中通常不会出现两次以上越行；假设4)～6)则是根据城市轨道交通快慢车运营实践得到的合理假设。

2 线路通过能力计算

线路通过能力采用的基础参数及符号如表1。由于快车每不停站通过1个站，相比慢车节约t节约min，因此从i站到j站，快车能节省nijmin。若i站为慢车站，则认为在该站节省时间由i站两边区间平分，j站同理。

2.1 无越行

无越行情况下，线路通过能力计算较为简单，只受追踪间隔及快车停站方案影响，如图1。根据假设快慢车运行时间差为n1mmin。快、慢车比例在为1∶1、 1∶2、 2∶1情况下的线路通过能力可通过周期时间乘以快慢车组合列车数，再除以快慢车组合最小周期时间确定，计算如式(1)～(3)：

(1)

(2)

(3)

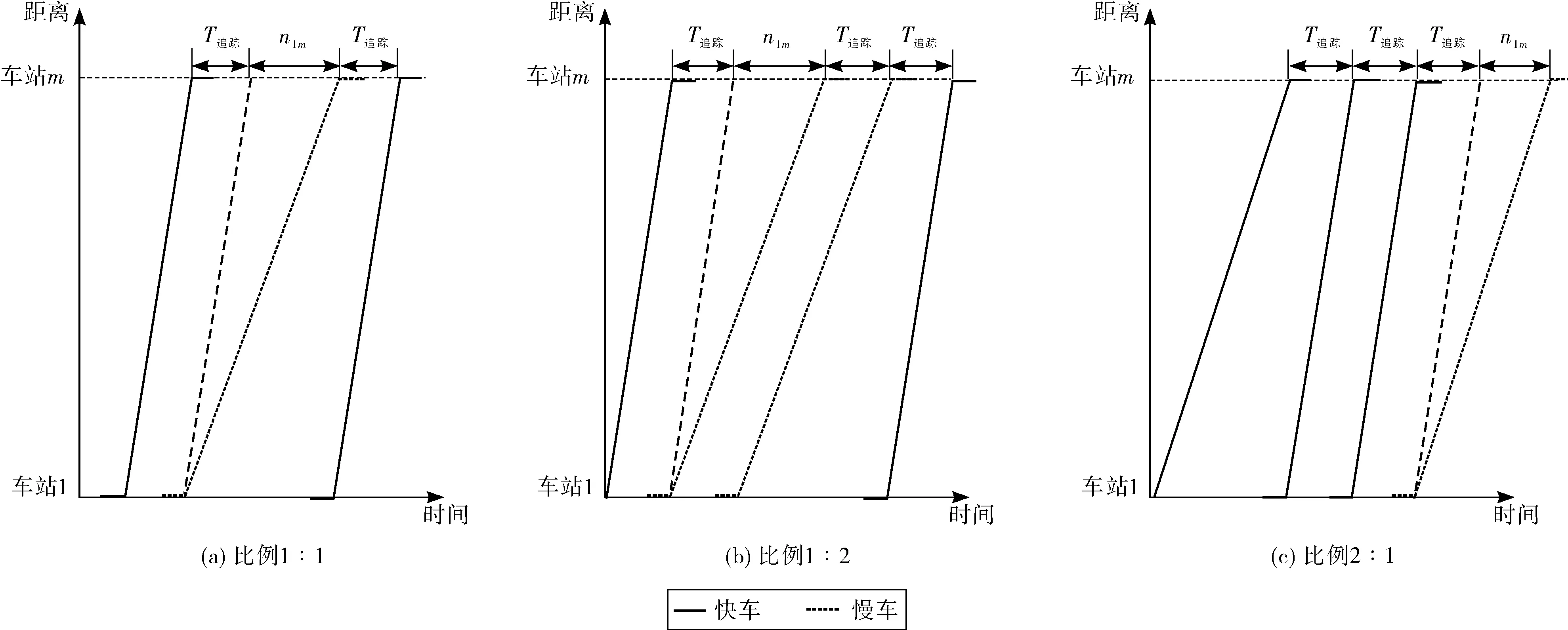
图1 无越行情况下线路通过能力计算

2.2 一次越行

对于发生一次越行情况，即慢车只被一列快车越行，则需分别讨论快慢车比例为1∶1、 1∶2、 2∶1这3种方案的通过能力计算。

快慢车比例为1∶1方案的线路通过能力如图2。与无越行相比，额外考虑了越行时间，慢车发车与到达时间可根据越行时刻推算得到。能力瓶颈点可能发生在车站m与车站1。故在越行一次时线路通过能力计算如式(4)：

(4)

图2 快慢车比例1∶1方案在越行一次时线路通过能力计算

快慢车比例为1∶2方案的线路通过能力与1∶1方案类似。加入了一趟慢车，由于只有一个越行站，因此加入的慢车不会被越行，考虑到无越行慢车最早发车时刻可能受前序慢车影响，也可能受前序快车影响，则需分别讨论，如图3。越行一次时线路通过能力计算如式(5)：

(5)

快慢车比例为2∶1方案在1∶1方案的基础上增加了一列快车，由于快车仅可能与前后慢车发生冲突，因此越行一次时线路通过能力计算只有一种可能，如图4。其计算如式(6)：

(6)

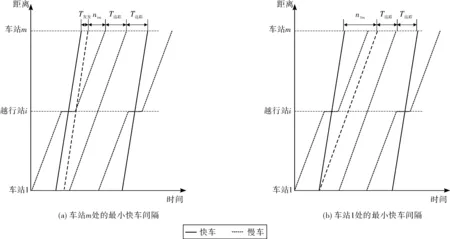
图3 快慢车比例1∶ 2方案在越行一次时线路通过能力计算

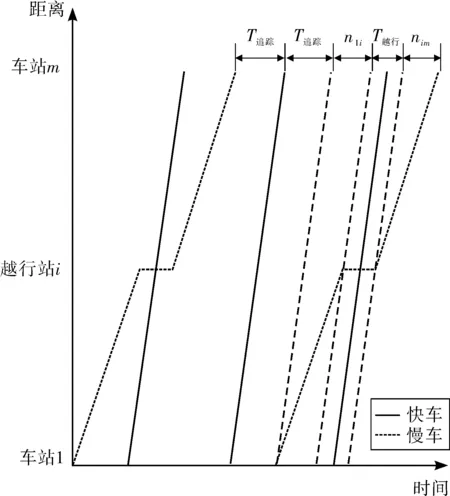
图4 快慢车比例2∶1方案在越行一次时线路通过能力计算

2.3 二次越行

对于二次越行情况，即慢车同时被两列快车越行，则需分别讨论快慢车比例为1∶1、 1∶2、 2∶1这3种方案的通过能力。

快慢车比例为1∶2的方案，快车越行两列慢车，能力瓶颈点可能发生在车站m与车站1，如图5。对于图5(a)，在车站m处慢车与第一列慢车间隔为t1=T发发+njm；第二辆慢车在快车经过越行站i后发车，第一辆慢车在快车经过越行站j后发车，因此慢车间隔t2至少为nij，此外还需要满足最小追踪间隔要求，因此t2=max{nij,T追踪}。图5(b)车站1处的通过能力计算类似，其中两列慢车的间隔时间为t′2=max{nij,T追踪}，快车与最近一辆慢车的间隔时间为t′1=T到到+n1i。故在越行两次时线路通过能力计算如式(7)：

(7)

图5 快慢车比例1∶2方案在越行两次时线路通过能力计算

对于快慢车比例1∶1方案，在两次越行时，线路通过能力如图6，慢车被两列快车越行，快车越行两列慢车。由于越行站固定，对于给定的慢车，快车只能在固定位置越行。故越行两次时线路通过能力计算如式(8)：

(8)

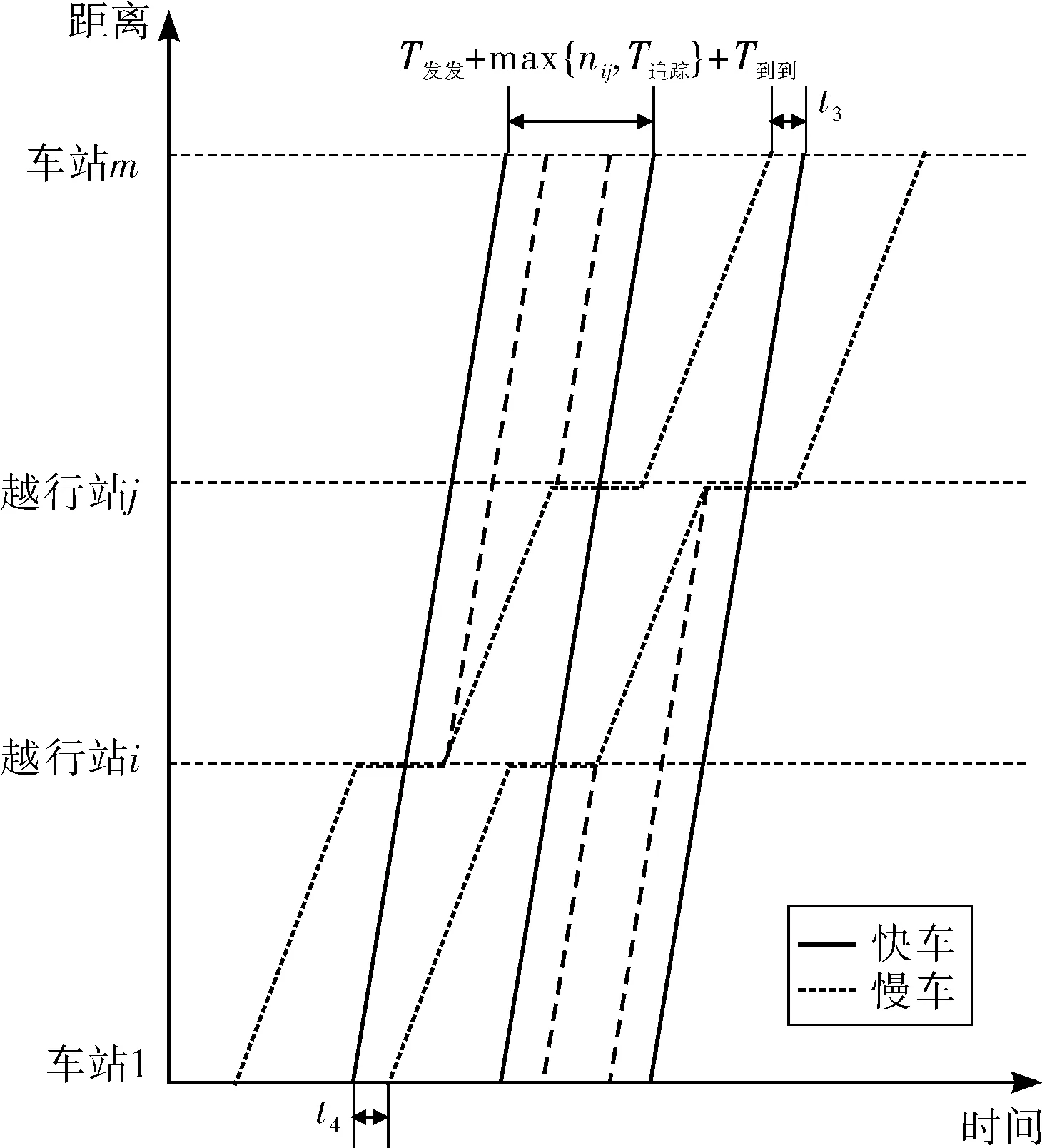
图6 快慢车比例1∶1方案在越行两次时线路通过能力计算

此外，考虑到慢车与快车间的安全距离，要求t3、t4均大于T追踪，其计算如式(9)、(10)：

t3=T发发+max{nij,T追踪}+T到到-T发发-njm≥T追踪

(9)

t4=T发发+max{nij,T追踪}+T到到-T到到-n1i≥T追踪

(10)

对于快慢车比例为2∶1方案，能力瓶颈点可能发生在车站m与车站1，如图7。其对应线路通过能力计算如式(11)：

(11)

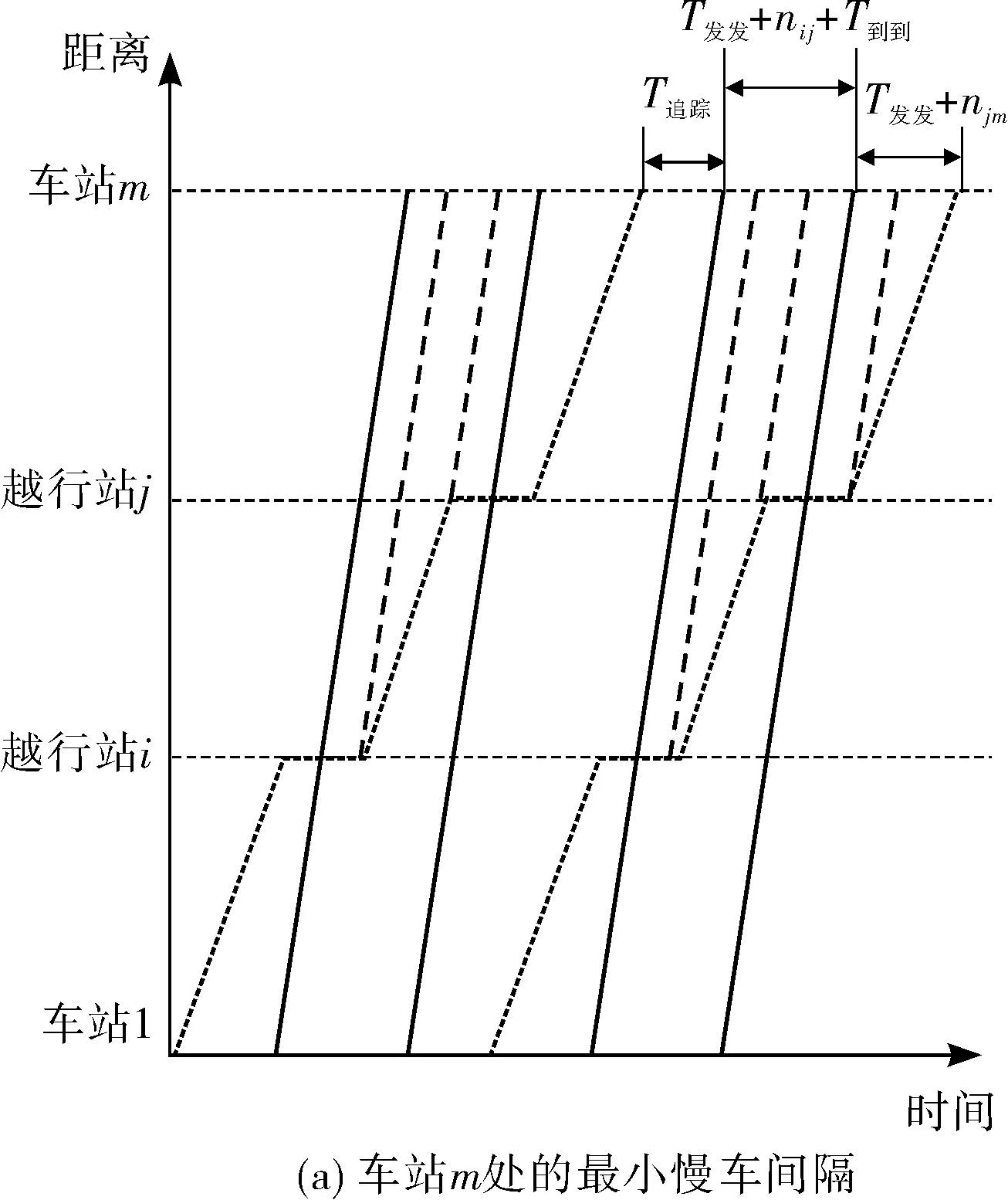
图7 快慢车比例2∶1方案在越行两次时线路通过能力计算

3 越行站设置影响分析

基于前文探讨越，笔者以福州某地铁线路为背景进行案例分析。该线路共有14个站，慢车站为第4、6、7、9、10站，在慢车站快车不停车通过，其中：第7、9、10站为越行站。最小追踪间隔为2 min，快车与慢车在越行站的最小到达间隔T到到= 1.5 min，最小发车间隔T发发=1 min，快车每次不停站通过节约时间t节约=1 min。

3.1 越行站数量对线路通过能力影响分析

越行站数量主要影响慢车被越行次数。以快慢车比例1∶1为例，在无越行条件下，快慢车组合最小周期时间为2T追踪+n1m。相较一次越行最小周期时间增加t1增加如式(12)；相较二次越行增加的时间t2增加如式(13)。

(12)

(13)

由此可发现：越行会减少因快慢车停站差异引起的周期时间增加，这部分时间受慢车站数量及慢车站与越行站位置分布影响，但是越行本身会增加周期时间，该时间受T发发、T到到影响。其余比例规律类似，不再赘述。考虑到T发发、T到到与T追踪的差距不会超过1 min，而每减少1个慢车站对最小周期时间影响，都可减少1 min的最小周期时间，故通常情况下增加越行就可减少最小周期时间，增加通过能力。此外因越行次数有限，额外增加越行站只会增加越行位置选择，不一定能保证得到更好的通过能力。

以福州线为背景进行测试，分别求得快慢车比例为1∶1、1∶2、2∶1的方案在无越行站、单一越行站、双越行站和三越行站情况下的线路通过能力如表2。为方便比较，并未取整，其中对于单一越行站情况，假设第9站为越行站；双越行站情况，假设第7、 9站为越行站；三越行站情况，由于最多二次越行，因此分别计算第7、 9站为越行站，第7、10站为越行站及第9、10站为越行站时的通过能力，取其中最大值；站站停方案按照最小间隔2 min发车。表2中：出现“*”的数据意味着通过能力在增加越行站后没有随之增加。其中快慢车比例2∶1方案在单一越行站情况下采用越行方案通过能力为15.65对/h，反而小于无越行站时的方案，故采用无越行方案；快慢车1∶1方案在双越行站情况下若采用两次越行方案，约束(10)检验不通过，会产生冲突，因此依旧按照单一越行站情况进行安排，其最大线路通过能力等同于单一越行站情况下能力。对于三越行站方案，只有快慢车1∶1方案由于在第7、 9站为越行站时无法满足越行约束(10)，而在第7、10站为越行站时可二次越行，增加了通过能力，其余方案下三越行站通过能力均无增加。

表2 线路通过能力统计

该结果印证了提出越行站数量对通过能力影响规律，可得到如下结论：① 当越行站数量小于最大允许越行的次数时，只要越行站位置合适且快慢车停站方案差异较大，有很大可能可增加通过能力；② 当越行站数量超过允许越行次数时，增加越行站只是提供更多越行位置选择，不一定能增加通过能力，边际效益降低；③ 快慢车方案相比站站停方案会显著减少线路通过能力，而在3种常见快慢车模式中，快慢车比例1∶2的方案通过能力最大。

3.2 越行站位置影响分析

在线路通过能力计算中经常出现多个能力瓶颈点。快车越行两列慢车时，慢车间的追踪间隔可能由最小追踪间隔确定，也可能根据越行时刻确定，体现在计算公式中用max{nij,T追踪}计算周期时间。能力瓶颈点可能在车站1发车时决定，也可能在车站m列车到达时决定，体现在计算公式中用max{T发发+nim,T到到+n1i}或max{T发发+njm,T到到+n1i}计算周期时间。故在选择越行站时，应该根据max函数中两边时间最相近的原则进行位置确定。对于单一越行站，需要设计越行站使得T发发+nim与T到到+n1i尽可能相等，考虑到T发发与T到到一般相差不大，因此应尽量让越行站两边的慢车站数量相等。对本案例中的线路而言，应该选车站7为越行站，此时的max{T发发+nim,T到到+n1i}最小，为4 min。

对于双越行站而言，同样需要使得两端终点站与相邻越行站之间的慢车站数量尽可能相等；此外因两个越行站过于接近会增加慢车额外停站时间，以保持慢车间安全间隔，故对于两个越行站之间的慢车站数量要尽量使得nij≥T追踪成立。对本案例中线路而言，应选择车站6、9作为越行站。采用改进后的越行站设置，可得到新的线路通过能力如表3。由表3可看出：单一越行站情况下，快慢车比例为1∶1方案的通过能力从17.14对/h上升到了21.82对/h；双越行站情况下，快慢车比例为1∶2方案的通过能力从22.5对/h上升到了25.71对/h。

表3 越行站改进后线路通过能力统计

4 结 论

笔者通过分类讨论得到了快慢车比例为1∶1、1∶2、 2∶1的3种方案在无越行站、单一越行站和双越行站情况下的线路通过能力计算公式。通过结合案例及对计算公式分析，得出如下结论：

1)增加越行站在一定程度上可增加通过能力，但不是越多越好；

2)在3种常见快慢车开行列车比例方案中，快慢车比例1∶2的方案通过能力最大；

3)越行站应根据被其分割线路中慢车站的数量进行确定而不是距离。合理设置越行站使得两端终点站与最近越行站之间慢车站数量尽可能相等，对于两个越行站情况，适当增加它们之间的慢车站数量，则可增加线路通过能力。