基于钻孔高压压水试验非线性流模拟计算错动带渗透参数*
周志芳 王 哲 李雅冰 沈 琪 李思佳 陈 朦
(①河海大学地球科学与工程学院,南京 211100,中国)(②生态环境部南京环境科学研究所,南京 210042,中国)
0 引 言
在工程项目建设过程中,往往需要开展大量水文地质、工程地质工作,为工程设计及安全施工提供决策依据(王洪波等,2018)。其中:压水试验已被广泛应用于岩土工程、水利水电工程和采矿工程等工程项目中(黄震等,2014;杨志斌等,2018),随着我国高坝枢纽工程和高水头电站的兴建,工程地质问题愈发突出(王启国等,2018;赵伟华等,2018),高压压水试验变得愈加重要。由于高压压水试验过程中会施加很高的水压力,且往往伴随着很大的渗流速度,这种情况下很容易出现非线性渗流。目前,生产实践中主要根据达西流公式计算水文地质参数,该方法不能满足高水头、高流速环境下的工程需要(黄勇等,2013),因此非常有必要对高压压水试验过程中出现的非线性渗流展开研究。
目前为止,Forchheimer方程和Izbash方程已被广泛应用于描述非线性渗流运动,前者有明确的理论基础和物理意义(Whitaker,1996);后者为经验公式。两种方程均能较好地表征非线性渗流运动(Chen et al.,2015)。很多学者对非线性渗流情况下的压水试验进行了研究(孟如真等,2014;毕宏伟等,2018;黄勇等,2018)。Quinn et al.(2011,2020)注意到压水试验过程中可能出现的两种非线性渗流运动,并提出了一种基于雷诺数的方法来提高非线性情况下渗透系数计算结果的可靠度。Zhang et al.(2013)开展了不同围压条件下裂隙岩体内非线性渗流试验,研究表明两种非线性方程均能很好地描述试验过程中出现的非线性渗流规律,并量化了非线性系数b。刘明明等(2016)对现行规范公式进行了拓展,建立了基于Forchheimer方程的裂隙岩体非线性参数计算公式。Zhou et al.(2018)结合现场试验,研究总结了高压压水试验的典型类型曲线,通过考虑不同的P-Q曲线来确定适当的渗透系数。周志芳等(2020a)将线性流情况下渗透系数K的倒数作为非线性系数a,在此基础上提出一种非线性系数b的计算方法,但这种确定a的方法可能存在一些问题。以上研究都是在稳定流的前提下,这些方法往往不能充分利用试验过程中的全部数据,无法反映试验过程中任意时刻下水头和流速的变化情况,因此求得的参数存在一定的局限性。
对于非稳定非线性渗流也有一些学者进行了研究。Wen et al.(2008a,2008b,2009,2013)充分研究了定流量抽水试验情况下非稳定非线性渗流的解析解与数值解,包括有无渗漏、完整井与非完整井等各种边界条件,并进行了理论分析。Wang et al.(2015)基于Izbash公式推导了微水试验的非稳定非线性流数值解,在此基础上研究了试验过程中非线性参数对水头的影响。Li et al.(2020)基于Izbash公式得到了变流量情况下非稳定非线性流的数值解,并对参数的敏感性进行了分析。这些非稳定非线性流的研究大都基于定流量或变流量抽水试验,而对于高压压水试验情况下阶梯水头的非稳定非线性研究鲜有报道。
综上所述,尽管对于高压压水试验的非线性参数的计算方法已有一定程度的研究,但仍存在一些不足。本文基于Forchheimer方程建立了基于高压压水试验的阶梯水头非稳定非线性渗流数学模型,并通过有限差分的方法得到其数值解,进一步对非线性参数进行了讨论,在此基础上结合工程实例反演得到错动带的非线性参数,对该方法进行了验证。
1 参数确定的原理
1.1 高压压水试验的渗流模型及其数值解
现场高压压水试验系统如图1所示。在钻孔内施加阶梯压力的水头,会形成一个倒置的降落漏斗。有如下假定:该系统中错动带均质各向同性,厚度处处相等、保持不变,产状水平且侧向无限延伸;错动带中的渗流为非线性流且流向是水平的;试验前天然状态下潜水面保持水平,且该系统为完整井并以阶梯压力注水。根据以上假设条件,高压压水试验过程中地下水运动的数学模型为:

图1 高压压水试验系统示意图Fig.1 The schematic diagram of high-pressure packer test system
(1)
h(r,0)=0
(2)
h(∞,t)=0
(3)
h(rw,t)=H(t)
(4)
式中:r为径向距离(m);t为压水时间(min);v(r,t)为t时刻径向距离r处的流速(m·min-1);h(r,t)为t时刻径向距离r处的水头(m);μ*为错动带的储水系数;M为错动带的厚度(m);rw为钻孔半径(m);H(t)为阶梯水头(m),可由h=Δp/γw换算得到,其中,γw为水的容重,即1MPa的压强可近似等于100m的水头h。
由于高压压水试验过程中,压水孔附近有很高的水头和渗流速度,这种情况下往往会出现非线性渗流,因此可采用非线性方程进行表征。因为Izbash方程为经验公式,且在描述径向非线性流问题上有一定局限(Wen et al.,2011),而Forchheimer方程具有明确的物理意义,所以本文采用后者来描述高压压水试验过程中的非线性渗流,Forchheimer方程可表示为:
(5)
式中:β和k均为非线性参数,其中,β表示非线性流中的惯性系数(min·m-1),k可表示错动带的表观渗透系数(m·min-1)。值得注意的是,当β等于0时,式(5)即为达西定律,此时k就等于错动带的渗透系数。
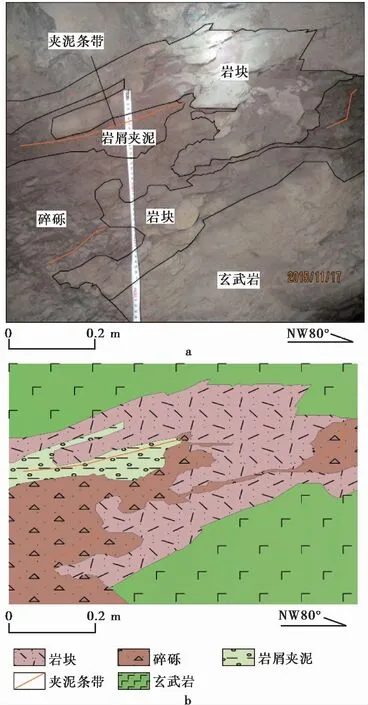
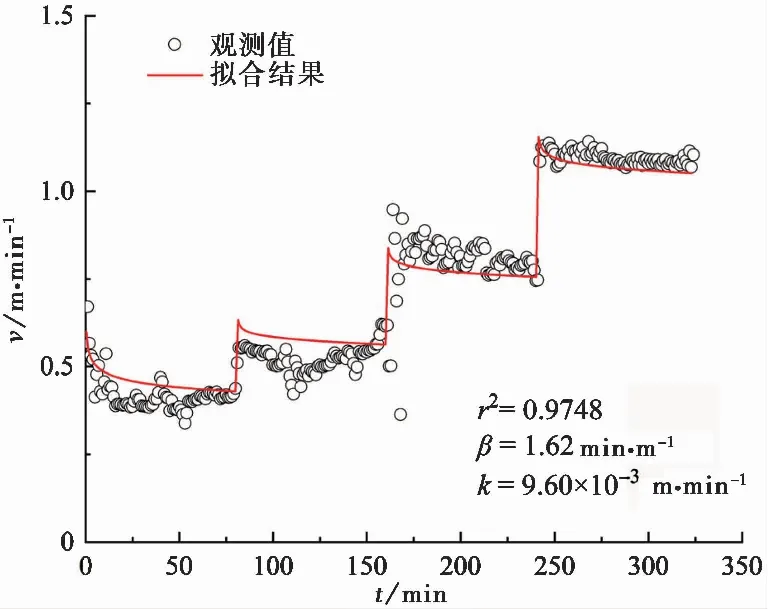
本文采用有限差分的方法对方程求解,首先在空间r上进行离散化,使用足够大的径向距离re来近似表示无穷远,即当r=re时,此处的水位变化约等于0。设节点个数为N,对空间域[rw,re]进行离散,ri表示第i个节点处的径向距离,rw ri=(ri-1/2+ri+1/2)/2,i=1,2,…,N (6) 由图1可知,在压水井附近的水位变化较大,距离压水井越远则水位变化越小,这种情况下需要在水位变化大的地方设置更加密集的差分网格,采用取对数的方式,有: i=0,1,…,N (7) 控制方程式(1)的差分格式为: i=1,2,…,N (8) 式中:hi和vi分别为在节点i处的水头和流速。根据式(5)可解得流速的表达式为: (9) 用差商近似代替导数,可得: i=2,3,…,N (10) i=1,2,…,N-1 (11) 在边界处的表达式为: (12) (13) 将式(10)~式(13)代入式(8),可以得到常微分方程式(8)的求解格式。当式中的各项参数已知,可通过Matlab软件进行编程求解任意时刻和径向距离处的水头及流速值。若已知试验观测数据,则可通过配线法或反演方法对参数进行求解,由于配线法过程中匹配点的选取存在一定的人为误差,在后文实例应用中将采用反演求参的方法。 求解上述问题过程中需要的水文地质参数主要有非线性参数β和k及错动带的储水系数μ*,有学者研究表明(Sen,1989),非线性渗流对错动带的储水系数μ*几乎没有影响,且μ*的变化范围一般在1×10-3~1×10-5之间,所以后文中主要针对非线性参数β和k进行讨论。为方便讨论,现对上述公式中的变量进行假设赋值,如表1所示。给定的高压压水试验阶梯水头压力值如图2所示。 表1 变量赋值表Table 1 Variable assignment table 图2 高压压水试验过程中的压力假定值Fig.2 The assumed pressure schedule of the packer test 非线性参数β和k对水头和流速变化的影响如图3、图4所示。为验证本文数值解的准确性,取β=0将上述数值解退化为达西流情况下的解,并与定水头注水条件下的达西流解析解进行比较(Jacob et al.,1952),如图3a所示。可见两种方法的计算结果基本一致,说明本文中的数值解是可靠的。 图3 非线性参数β和k对水头变化的影响Fig.3 The influence of nonlinear parameters β and k on the change of water heada.β对水头变化的影响;b.k对水头变化的影响 由于高压压水试验过程具有施加阶梯水压的特点,在升压时间节点前后任意径向距离处的水头具有明显的跳跃式增加,随后缓慢增加最终趋于稳定,且β或k越大其突变增量越小。由图3a可知,当r和k保持不变时,在某一压力阶段情况下,随着β的增加,该径向距离处的水头逐渐减小,这是因为β增大使得每米水头变化所需的时间增加,且β越大将会使得高压压水试验更早地接近稳定状态(图4a),所以较大的β会导致整个高压压水试验期间的水头总体减小。由图3b可知,当r和β保持不变时,在某一压力阶段情况下,k越大同样会导致试验期间的水头变化越小,可通过式(5)进行解释,β和v保持不变的情况下,k越大则说明水力梯度越小,进而对应位置处的水头也越小。另外,从图3b中还可以看出,k越大,试验达到稳定状态所需的时间也越短。 图4 非线性参数β和k对流速变化的影响Fig.4 The influence of nonlinear parameters β and k on the change of flow velocitya.β对流速变化的影响;b.k对流速变化的影响 总体来看,图4中流速的变化与图3中水头的变化有相似之处,整个高压压水试验过程中,在升压时间节点前后任意径向距离处的流速同样有明显的跳跃式增加,随后逐渐减小最终趋于稳定,且β越大或k越小其突变增量越小。在某一压力阶段情况下,从图4a中可以看出,当k和r保持不变时,试验过程中的流速v随β的增加而减小;同样地,从图4b中可以看出,当β和r保持不变时,试验过程中的流速v随k的增大而增大。非线性参数β和k对流速的影响均可通过式(5)进行解释,k和∂h/∂r不变的情况下β增大会导致流速v减小,β和∂h/∂r不变的情况下k增大会导致流速v增大。综上所述,如果不考虑试验过程中非线性参数的影响,仍按照达西流公式进行计算,将无法得到合适的水文地质参数,将会高估错动带中的水头,进而高估结构面抵抗渗透破坏的能力,最终对工程稳定性产生影响。 以白鹤滩水电站坝址区为例,选定白鹤滩水电站坝址区两侧山体内的C2层间错动带为对象进行现场高压压水试验,对本文给出的方法进行验证并确定该错动带的非线性参数。 坝址区两侧山体内的玄武岩中广泛发育有缓倾角、贯穿性的层间错动带,且部分错动带位于水库蓄水位以下,对地下厂房渗漏和坝址区整体渗透稳定性有直接影响(周志芳等,2020b)。白鹤滩水电站地下厂房开挖后,进一步证实坝址区水文地质条件复杂,亟需对错动带的水文地质参数进行研究。C2错动带主要出露于左岸厂房主变交通洞和截渗洞,错动带因构造错动而形成,其内部物质成层性较为明显。地下水侵蚀形成次生泥,厚度1~4cm,错动带内物质较为破碎和松散,多发育有岩屑夹泥和碎砾,其中岩屑宽度1~12cm,碎粒宽度5~50cm。由于夹泥和岩屑夹泥多近水平方向发育,垂直结构面方向上的透水性减弱,同时由于上下两盘围岩较为破碎,破碎带宽度多形成节理或劈理构造,透水性增强,因此围岩裂隙常见滴水或线状流水。以左岸厂房C2截渗洞处错动带为例,其出露情况如图5所示,可见其出露展布起伏变化较大,总体厚度为20~40cm,各充填物在错动带中的成层状特征不明显,部分错动带中含有岩块透镜体。错动带中夹泥含量较少,岩屑和碎砾发育较为紧密坚硬,黏土含量较低。 图5 左岸厂房C2截渗洞C2错动带照片及示意图Fig.5 The photo and schematic diagram of C2 staggered zone at the interception tunnel of the left bank planta.C2错动带照片;b.C2错动带示意图 本文选择揭露了C2错动带的CZK57钻孔组进行高压压水试验,钻孔组位于左岸尾闸通气兼安全洞,钻孔采用水钻钻进工艺,共计完成3个试验孔,孔口地面高程为636.6m,相应的试验孔编号依次为CZK57-0、CZK57-1、CZK57-2。钻孔完成钻进后,采用高压清水进行洗孔处理,并对钻孔内情况进行钻孔电视记录。根据钻孔电视记录和钻孔岩芯编录成果,钻孔中C2错动带出露深度及各钻孔位置如图6所示。 图6 CZK57钻孔组布置及剖面示意图Fig.6 The layout and profile diagram of CZK57 boreholea.CZK57钻孔现场布置图;b.CZK57钻孔布置剖面图 将CZK57-1作为压水孔,其余两个钻孔作为观测孔。高压压水试验采用梯级升压法,针对该次试验制定了4级压力的试验规程,即0.5MPa(80min)→0.7MPa(80min)→1MPa(80min)→1.5MPa(83min),按照该过程逐级升压。为保证施加的水压能全部作用在错动带内,钻孔清洗完毕后、试验开始前在错动带附近安装了止水栓塞。试验过程中,采用流量表和全自动压力探头分别记录试验孔处的流量和压力等数据,试验结果如图7所示。由图7可见,升压时间节点前后试验孔处流量有明显的跳跃式增加,各级压力阶段下试验孔内的流量呈减小趋势且减小的速率也越来越小,最终趋于稳定,试验结果与前文中理论分析部分相吻合。 图7 高压压水试验过程中流量及压力变化情况(CZK57-1)Fig.7 The changes of flow rate and pressure during the packer test(CZK57-1) 根据高压压水试验结果可以反演得到C2错动带的非线性参数,本文以PEST反演为例进行介绍,PEST参数估计方法的基础为Marquardt-Levenberg算法,其原理为将模型计算值与实测值的误差建立为差异函数,将参数优化问题转化为求取目标函数最小值的问题。操作步骤如下,首先要处理实测数据,由于观测值为压水孔处的流量Q(L·min-1),应将其换算为流速v,根据v=Q/(2πrwM)可换算得到井径处的流速,并将观测值保存至数据文件。其次,需要获得模型计算值,用Matlab编写由式(8)及式(10)~式(13)组成的数值解求解程序,进而可以计算得到估计值。然后,编写PEST程序计算所需的模板文件、控制文件和指令文件,其中控制文件是PEST的核心,应在该文件中设置好待优化参数个数、初始参数取值和优化参数的取值范围等信息。最后运行PEST程序进行参数反演,可以得到最优的参数结果。计算过程中涉及到的常量与表1内数值相同,设定β和k的初始值分别为2.0min·m-1和1.0×10-2m·min-1,取值范围分别为[1.0×10-3,1.0×103]min·m-1和[1.0×10-4,10.0]m·min-1,反演及拟合结果如图8所示。 图8 试验孔流量观测值与拟合结果Fig.8 The measured flow rate of the test borehole and the fitting results 在上述给定参数初值和取值范围内,经PEST反演后得到C2错动带非线性参数β=1.62 min·m-1,k=9.60×10-3m·min-1,其拟合相关系数r2=0.9748,结果表明高压压水试验过程中错动带内的确发生了非线性渗流,且本方法能得到较好的计算结果。从图8可以看出,拟合曲线与实际观测值具有相似的变化规律,拟合效果较好,局部曲线会与实测数据有一些偏离,可能的原因为:现场试验的地质条件往往比较复杂,较高的水压力会带走错动带内一部分充填物,透水介质的内部结构会发生一定的变化,则其渗透系数或非线性参数会发生改变,通常情况下透水介质的渗透性会增大,使得实测流速v增大,进而导致拟合曲线与实测数据有一些偏差,在后两个压力阶段实测流速v略高于估计值,但总体上来看反演及拟合结果是可靠的。 将本文反演得到的k、β换算成周志芳等(2020a)中的a,b分别为a=1/k=62.5s·cm-1,b=β/k=60.8s2·cm-2,结果与该文献方法确定的非线性参数的几何平均值a=43.36s·cm-1、b=30.63s2·cm-2比较接近,由于该文献方法是预设的a值,然后根据4个压水阶段的流量稳定值计算求得b,而本文方法利用了整个试验过程中的所有流量数据点(图8),因此本文方法得到参数结果更加精确、可靠。 本文采用有限差分的方法得到了高压压水试验情况下错动带中非线性渗流的数值解,在此基础上分析了非线性参数对水头和流速的影响,并结合现场高压压水试验反演得到了错动带的非线性参数。主要结论如下: (1)将本文得到的数值解(取β=0)与定水头注水条件下的达西流解析解进行比较,发现两种方法的计算结果基本一致,可以说明本文数值解是准确可信的。 (2)由于高压压水试验施加阶梯水压的特点,在升压时间节点前后水头h和流速v均有明显的跳跃式增加,随后逐渐趋于稳定。当非线性参数k和径向距离r保持不变时,非线性参数β越大则整个高压压水试验过程中的水头h和流速v都越小;当非线性参数β和径向距离r保持不变时,k越大则整个高压压水试验过程中的水头h越小、流速v越大。另外在高压压水试验情况下,较大的β和k均会使得试验能更快地达到稳定状态。 (3)白鹤滩水电站现场高压压水试验验证表明,试验过程中错动带内的确存在非线性渗流,且根据本文推导的非线性流数值解,采用PEST反演的方法能得到较好的计算及拟合结果,该方法利用了整个试验过程中的所有流量数据点,因此得到参数结果更加精确、可靠。白鹤滩水电站C2错动带的非线性参数β=1.62min·m-1,k=9.60×10-3m·min-1。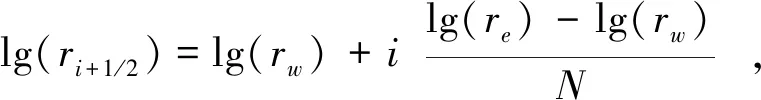

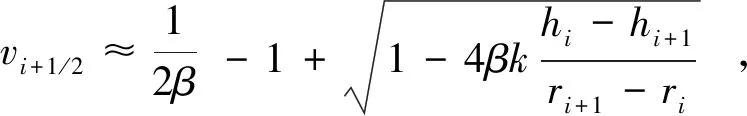
1.2 非线性参数的讨论




2 工程实例
2.1 工程概况
2.2 试验方案及数据


2.3 非线性参数的确定
3 结 论

