基于无味变换的边坡可靠性分析

向子林，许晓亮，黄闻捷，陈将宏

(三峡大学 a. 水利与环境学院；b. 三峡库区地质灾害教育部重点实验室；c. 电气与新能源学院，湖北 宜昌 443002)

由于边坡工程岩土体力学参数及破坏模式的随机性和复杂性，可靠性分析逐渐成为了边坡稳定评价及工程设计的另一主要途径和参考依据[1-2]。

目前，在边坡可靠性分析方面的研究大致可以分为两类[3]。一类是边坡单一破坏模式的单元可靠性分析，如：祝玉学等[4]研究了岩质边坡双滑面破坏模式的可靠性计算方法；Low[5]提出了基于Excel的可靠指标计算新算法，并将结果用于岩质边坡单滑面破坏的可靠度分析，采用Beta分布描述黏聚力和摩擦角的分布，采用截尾指数分布描述张裂缝中充水深度系数的分布。第二类是多滑面或多个失效模式的边坡体系可靠性分析，如郑智洋等[6]利用双折减系数法对多滑面边坡稳定性进行分析和研究；谭晓慧等[7]采用Ditle-vsen窄界限公式估算了岩质边坡各失稳模式组成的串联体系的可靠指标；Jimenez-Rodriguez等[8]提出了采用不相交的割集来分析楔体多失效模式的体系可靠度问题，并采用顺序条件重要抽样方法计算体系可靠指标。

与此同时，在传统的一阶可靠度分析方法(first-order reliability，FORM)、蒙特卡洛法(Monte Carlo method，MCS method)、响应面法(response surface methodology，RSM)的基础上，新的边坡可靠性分析方法也不断得到了丰富和发展，如随机有限元法[9]、重要抽样法[10]、copula积分法[2,11]，分别在变量相关性描述、高效抽样、功能函数逼近方面做了有益的探索。上述方法中，蒙特卡洛法作为计算失效概率最直接的方法，其计算精度高，已被广泛应用，但当需要大量抽样时，蒙特卡洛法的计算效率较低，特别是对于复杂系统的多维相关变量及非线性问题的求解；此外，工程中比较常用的中心点、验算点等一阶可靠度分析方法通常需要将相关非正态变量进行独立化和标准化[12]，增加了计算的近似程度与复杂程度。

因此，有必要进一步探究具有更大灵活性、更高计算效率和更强非线性处理能力的边坡可靠性分析方法。无味变换[13-16]是利用变量的均值和协方差来近似其非线性转换后变量统计特性的方法，相对于蒙特卡洛及一阶可靠度分析方法等，具有计算效率高、精度高(均值、协方差传播精度均可达到二阶以上)、不依赖于分布类型以及应用方便(无需求解非线性方程的Jacobi矩阵[14]，甚至无需知道非线性方程的显式方程)等优点，能够较好地处理高维抽样及非线性传递问题，已在自动控制、导航制导、人工智能等领域得到成功的应用[13]。笔者将无味变换引入到边坡可靠性分析之中，给出了基于无味变换的边坡可靠性分析方法，开展了算例边坡的可靠度指标和失效概率计算，并通过不同方法结果的对比分析，阐述所提出方法的合理性和适用性。

1 基于无味变换的边坡可靠性分析方法

1.1 无味变换原理介绍

传统线性化方法的基本思路是对非线性映射做某种线性近似，然后再运用各种线性近似的方法进行分析，相比较于传统的线性化方法，用有限的参数来近似随机变量的概率特性要比近似任意的非线性映射函数更为容易，而且用更少的计算量可以达到更高的精度。基于此，Savin等[15]、Julier等[16]提出了无味变换(unscented transformation，UT)，其核心在于借助有限个特征点的信息来近似表达n维随机变量的整体信息(概率密度函数)。

假设有随机变量x的均值矩阵为mx，协方差矩阵为Vx，随机变量y是关于x的函数，通过式(1)所示方式进行映射。

y=f[x]

(1)

式中：f为非线性映射。基于此可计算出y的均值矩阵my和协方差矩阵Vy。

依据无味变换原理[15-16]，对于n维随机变量x，可用2n+1个σ点来近似其概率密度函数信息，在n维空间中的σ点Xi(i=1,2,…2n)的定义为

X0=mx

(2)

(3)

(4)

(5)

式(3)和式(4)中协方差矩阵Vx需要进行平方根分解；式(5)中λ为尺度参数，其计算方式为

λ=α2·(n+k)-n

(6)

式中：α是小于1的正数，表示由于阶数的变化而对σ点集的收集造成的影响，依据文献[16]，为将阶数的影响降至最低，取α=10-3；常数k的确定方式为

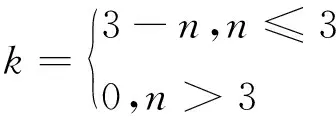
(7)

式中：n为随机变量个数。

基于计算得到的σ点，通过式(1)的非线性映射可对上述σ点进行非线性转换。

Yi=f[Xi]

(8)

然后利用非线性转换后σ点的权值来计算出随机变量y的均值my和协方差矩阵Vy。

(9)

(10)

式中：Wi为第个i点的权值；Wi(m)为用来计算均值的权值；Wi(c)为用来计算协方差矩阵的权值，其计算式为

(11)

(12)

Wi(m)=Wi(c)=1/[2·(n+λ)]，i=1,2,...，2n

(13)

式中：当服从高斯分布时，η可以取2[15]；式(3)～式(13)为变尺度无味变换的计算方法；当α=1、η=0时，对应为标准无味变换方法。

1.2 基于无味变换的边坡可靠性分析步骤

无味变换计算效率高，运用方便[13]，能够用有限的数据点信息近似整体概率分布信息，且不依赖于变量的分布类型，可用于边坡工程的可靠性分析。此时，通过确定抗剪强度参数黏聚力c和摩擦角φ等随机变量的均值、方差，并借助FS=f(c，φ,…)映射关系(即功能函数)，便可得出安全系数FS的均值方差，进而计算边坡的可靠度指标β及失效概率Pf。图1给出了基于无味变换的边坡可靠性分析方法的技术路线，其主要实施步骤：1)分析选定对边坡可靠性更为敏感的参数作为随机变量，如通常将边坡土体的黏聚力c和摩擦角φ作为随机变量[11]；2)根据参数黏聚力c和摩擦角φ的均值、方差及相关系数ρcφ，计算得到随机变量的均值矩阵和协方差矩阵；3)利用Step2得到的协方差矩阵进行平方根分解，并结合均值矩阵和引入的尺度参数，计算得到2n+1个σ点，见式(2)～式(7)；4)建立目标边坡计算模型，同时，将Step3得到的2n+1个σ点代入模型，并开展二维极限平衡计算，通过搜索最危险的滑面，得到2n+1个安全系数FS的值，见式(8)；5)利用权值的定义和λ、η等参数，分别得出2n+1个FS的均值和协方差的权值，见式(11)～式(13)；6)根据Step4得到的2n+1个FS值，并结合Step5计算得到的权值，分别借助式(9)、式(10)计算得到FS的均值和方差；7)借助可靠度指标的定义(均值与标准差的比)直接计算边坡可靠度指标β值，同时，可借助失效概率与可靠度指标的关系进一步计算相应的失效概率。

图1 基于无味变换的边坡可靠度分析方法Fig.1 Slope reliability analysis method based on

2 算例分析

2.1 均质边坡算例

算例1为软土层上的均质边坡[17]，典型剖面见图2，图中各层土体的参数见表1，且分布类型为正态分布[17-18]。借助Slide软件，采用简化的Bishop法进行极限平衡计算，得出坡体参数采用均值时的安全系数为1.165，安全系数与最危险滑面的位置均与Cho[18]计算(FS=1.164)非常接近。

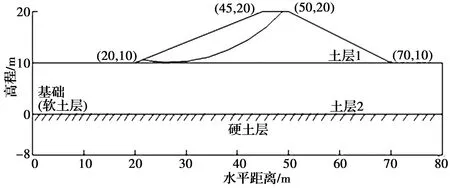
图2 均质边坡计算剖面Fig.2 Calculation section of homogeneous

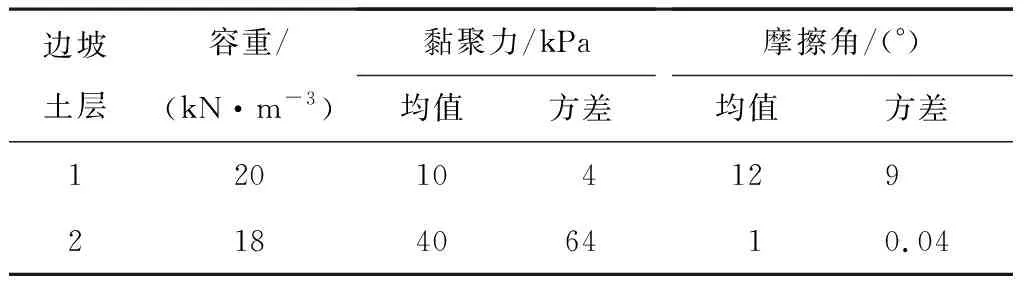
表1 算例1边坡土体参数统计特性Table 1 Statistical characteristics of soil parameters of slope in example 1

在不考虑边坡土体黏聚力c和摩擦角φ的相关性时，根据表1土体参数黏聚力c和摩擦角φ的均值和方差，计算得到个9个σ点，并利用Slide开展二维极限平衡计算，从而得到9组安全系数，如表2所示，进而通过无味变换的边坡可靠度分析法得到算例1中边坡的失效概率为19.66%，与相应蒙特卡洛法(MCS)和一阶可靠度分析(FORM)验算点法得到的失效概率计算结果基本一致，相对误差在6%以内，如表3所示。

表2 算例1的σ点和安全系数Table 2 σ point and safety factors in example 1

表3 坡体c和φ独立时失效概率结果对比Table 3 Comparison of failure probability results when c and φ of the slope are independent

在考虑边坡土体抗剪强度参数间相关性时，表4为给出不同c和φ的相关系数ρcφ条件下分别采用无味变换法及蒙特卡洛(MCS)模拟得到的边坡失效概率。由于边坡主要的破坏模式(最危险滑面)均出现在土层1，土层2参数对于边坡稳定性及可靠度结果几乎没有影响，计算中土层2中c和φ的相关系数与土层1保持一致。综合表3和表4可知，在ρcφ由负到正的过程中，边坡失效概率明显增大，土体黏聚力c和摩擦角φ的相关性对坡体可靠性分析结果影响显著，这与一般结论相吻合[11,20]。

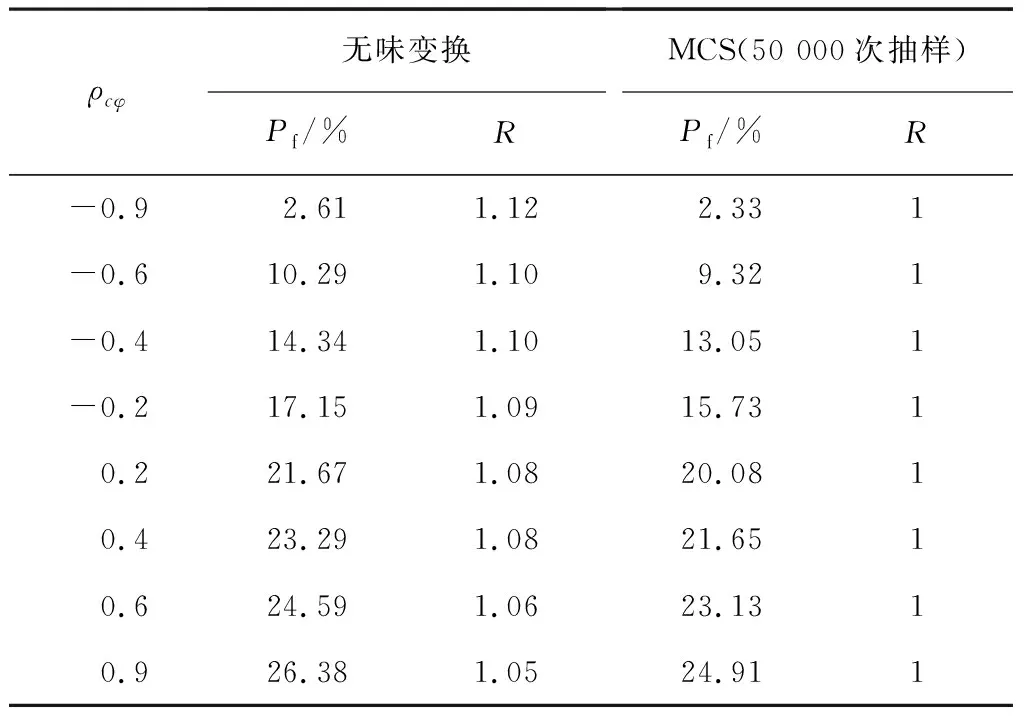
表4 考虑不同相关系数的失效概率Table 4 Failure probability considering different correlation coefficients

此外，表4还给出了以MCS的失效概率为基准值的当量比值R，其结果介于1.05～1.12之间，且随着c和φ的负相关性逐渐增强(ρcφ逐渐减小)，R值逐渐增大，即无味变换法的相对误差δ(δ=|R-1|×100%)不断增大，而当c和φ呈现正相关关系时，R≤1.08，即相对误差均在8%以内。进一步分析可知，造成上述误差变化的主要原因在于失效概率量值的差异性，失效概率量值较大时，两种方法结果的差异性越不显著，反之，引起的相对误差较大。可见，本例中，在较低失效概率(Pf<15%)时，可靠性分析结果对计算方法的选择比较敏感。

2.2 分层边坡算例

算例2为一个分层边坡，计算剖面见图3，边坡土层参数见表5，不确定参数服从正态分布[21]。采用抗剪强度参数均值，应用简化的Bishop法得出相应的坡体安全系数为1.509。

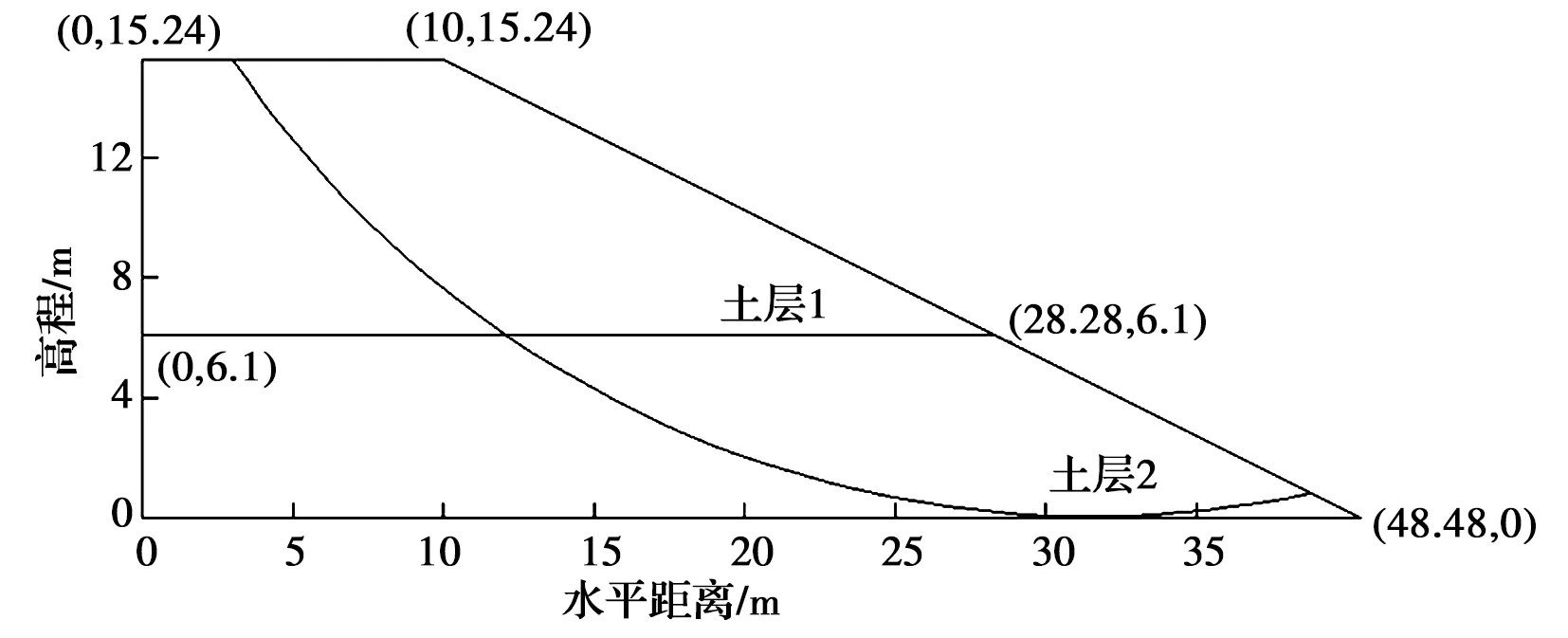
图3 分层边坡剖面

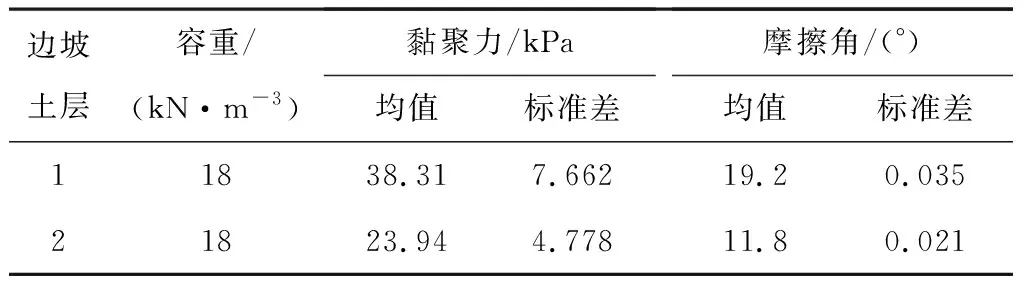
表5 算例2土体层数统计特征Table 5 Statistical characteristics of soil layers in example 2

本例中，两层土坡共涉及抗剪强度参数黏聚力c和摩擦角φ等4个变量，依据表6中相关系数及各变量的均值和方差获取相应的均值矩阵及协方差矩阵，进而确定出9个σ点，得出基于无味变换的边坡可靠度指标β，见表6。

为分析两种方法结果的差异性，表6中还给出了以文献[21]中MCS得出的可靠度指标为基准值的当量比值R，同时，图4给出了无味变换与蒙特卡洛法[21](MCS)计算结果的对比。分析发现，ρcφ越小，(负相关性越显著)R值越大，β>3时，相对误差整体超过了10%，但进一步结合图4和表5分析发现，本例中坡体安全系数达到1.509，整体可靠度指标较大，特别是当ρcφ越小时，β越大，相应Pf更低，与算例1所述相同，说明较低失效概率易增加不同计算结果的差异性。

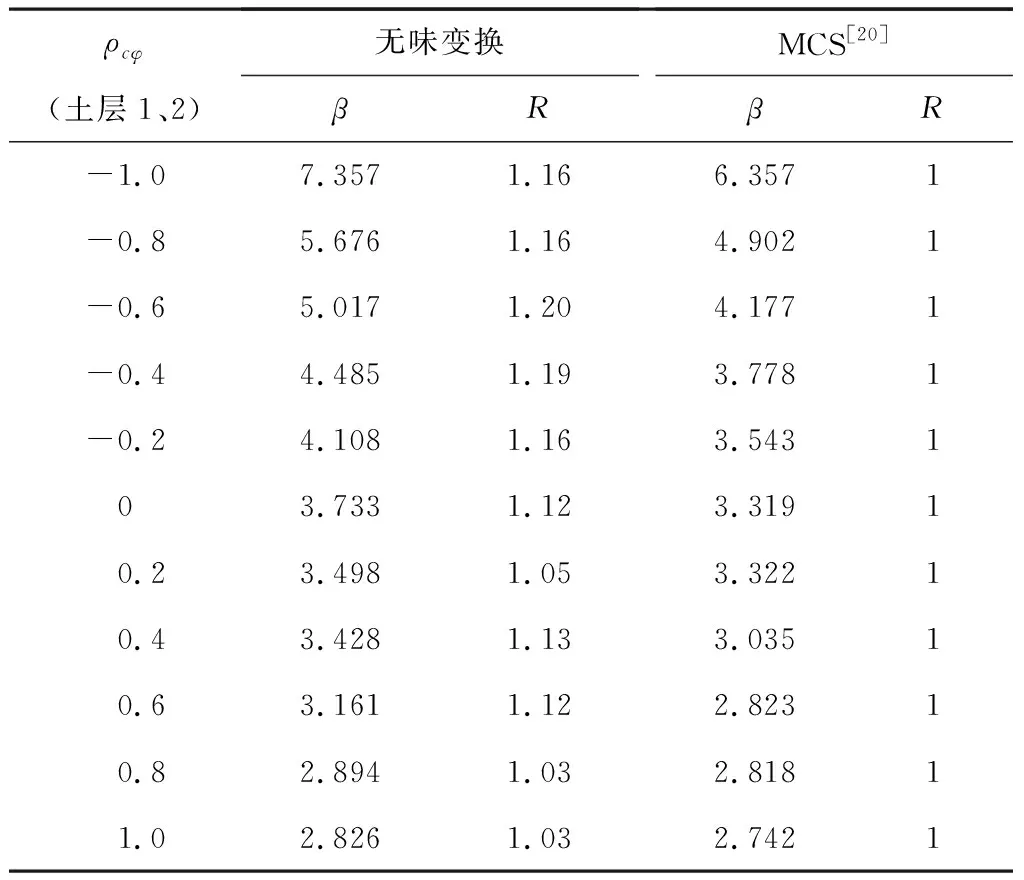
表6 考虑不同相关系数的可靠度指标Table 6 Reliability index considering different correlation coefficients

图4 无味变换及MCS的可靠度指标对比Fig.4 Comparison of reliability indexes between unscented

为进一步验证上述结论，通过不同程度地降低坡体土层c和φ的均值，即减小坡体安全系数，增大相应失效概率，得出了不同安全系数下无味变换法和MCS法的可靠度指标，见表7和图5。由表7和图5可见，边坡安全系数越小、可靠度越低时，相关系数的变化引起的误差波动越小，在β<1.5，即Pf>7%时，相对于MCS法，基于无味变化方法得出的误差均在5%以内，两种方法的计算结果差异性较小。

图5 不同安全系数下两种方法的可靠度指标对比Fig.5 Comparison of reliability indexes of two methods

可见，相对于稳定性较好的边坡，基于无味变换的边坡可靠性分析方法能更好地应用于较低可靠度β<1.5(较高失效概率,Pf>7%)的坡体分析中，而该类边坡往往是工程中更为关注的对象，进而体现了所提出的基于无味变换的边坡可靠性分析方法的适用性。

3 计算效率分析

为了更好地说明基于无味变换的边坡可靠性分析方法的计算效率，从花费的计算时间角度分别对算例1和算例2进行了分析。基于无味变换的边坡可靠性分析的计算时间由3部分组成：利用Matlab计算得到σ点的用时，利用σ点开展二维极限平衡计算，得到安全系数和利用无味变换法进行失效概率计算的用时。对于算例1和2，表8给出了以上各部分计算用时及总时间情况。

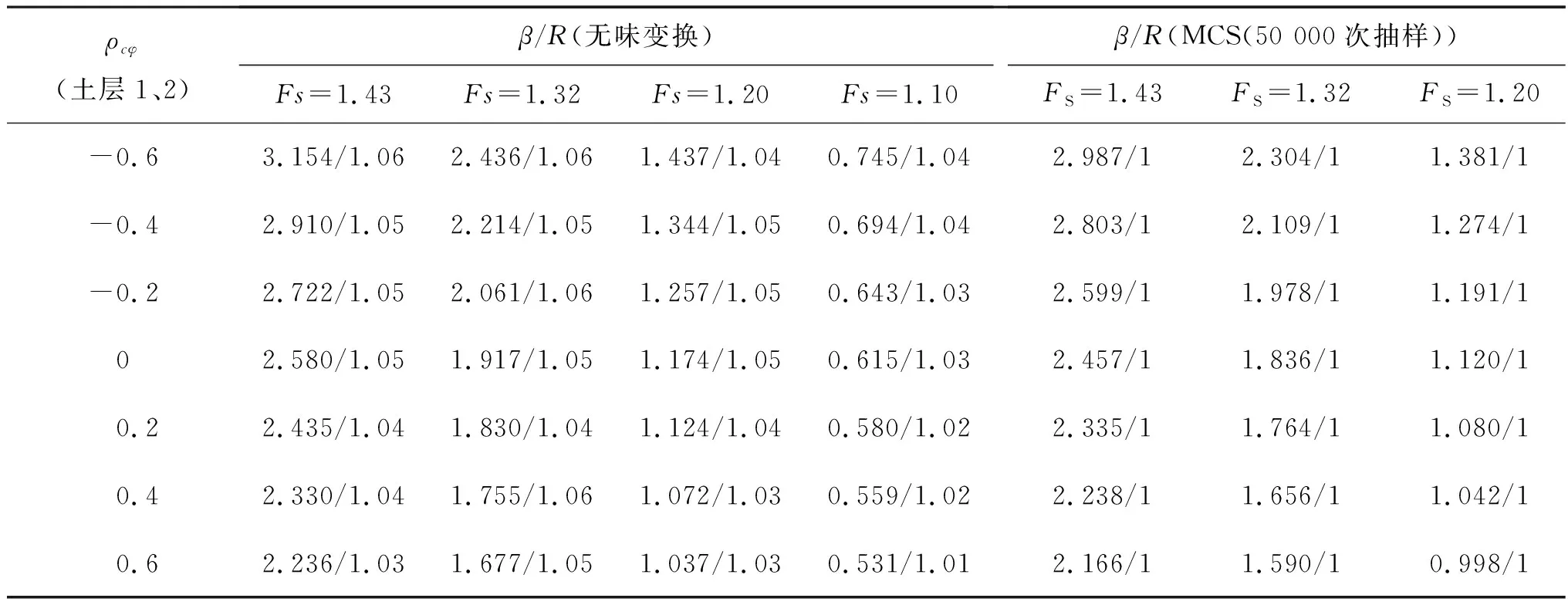
表7 不同安全系数及不同相关系数下的可靠度指标Table 7 Reliability index under different safety factors and different correlation coefficients

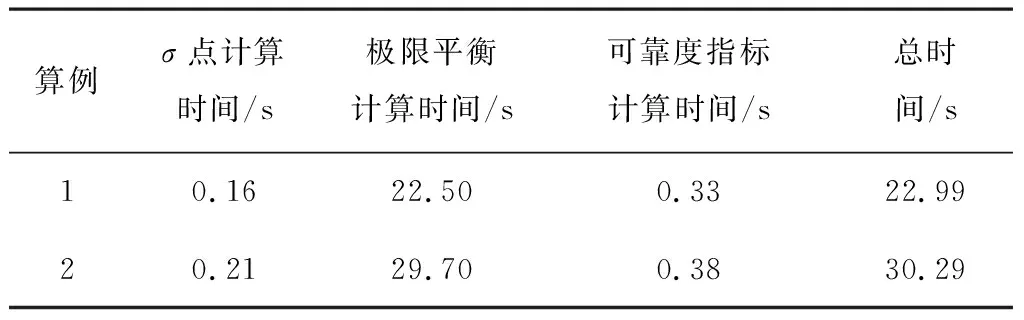
表8 利用无味变换进行边坡可靠性分析的时间Table 8 Time for slope reliability analysis from unscented transformation

同样，仍以蒙特卡洛法作为对比对象，由于该方法计算时间与计算精度均与抽样次数有关，一般需要进行20 000次以上的模拟才会收敛[22]，同时，抽样次数越多，计算精度越高，但耗时更长。故分别选取20 000次(所需最少计算次数)和500 000次的蒙特卡洛模拟与无味变换方法进行计算时间对比，两种方法均考虑变量相互独立的情况，且均在配置内存为8 GB、处理器为Intel(R)Corei7、CPU主频为2.00 GHz的计算机上进行，计算用时结果如表9所示。显然，两个算例中，相对于蒙特卡洛模拟，无味变换方法用时更少，效率更高，对于最少计算次数(20 000次抽样)和较高精度(500 000次抽样)的蒙特卡洛模拟，算例1(均质边坡)中，无味变换法用时分别减少了17.9%和58.95%，而对于非均质边坡(算例2)，无味变换法用时分别减少了8.21%和55.46%。

表9 无味变换和蒙特卡罗计算时间及次数对比Table 9 Comparison of calculation time and frequency between unscented transformation and Monte Carlo

4 结论

1)基于无味变换的边坡可靠性分析方法应用方便，不依赖于变量的分布类型，能够显著提高计算效率，对于有n个主控随机变量的功能函数，只需2n+1次计算。

2)算例结果显示，在低失效概率时(Pf≤7%)，基于无味变换方法的计算结果误差达到5%以上，可靠性分析结果对计算方法的选择较为敏感，直接采用基于无味变换的方法会引起对可靠性结果过高的估计；但对于工程中关注更多的较高失效概率(Pf>7%)的边坡，基于无味变换方法计算结果相对误差在5%以内，且相关系数的变化引起的误差波动较小，适用性好。

3)借助无味变换原理丰富了边坡可靠性分析方法，但针对低失效概率条件下计算误差较大的内在机理以及如何实现较高计算精度的问题，还需从推求具有更佳逼近效果的σ点入手展开进一步的探索，期待提出的基于无味变换的边坡可靠性分析方法有更多的关注与发展。