碰摩转子—油膜轴承系统的全局动力学研究

曾旭焱，侍玉青，刘军，郭遥

碰摩转子—油膜轴承系统的全局动力学研究

曾旭焱1, 2，侍玉青1, 2，刘军1, 2，郭遥3

(1. 兰州交通大学 机电工程学院，甘肃 兰州 730070；2. 甘肃省轨道交通装备系统动力学与可靠性重点实验室，甘肃 兰州 730070；3. 湖南工商大学 计算机与信息工程学院，湖南 长沙 410205)

考虑滑动轴承的非线性油膜力和转定子的碰摩力，建立了含碰摩故障的单盘转子-滑动轴承耦合系统动力学模型。运用四阶变步长的龙格-库塔-基尔法获得系统的非线性响应，利用Poincaré型的简单胞映射法对转子系统进行了全局动力学分析。研究结果表明：随着转子转速的增加，系统存在多个周期解共存以及周期解与混沌解共存现象。最后列举了转子系统在不良参数条件下，通过合理控制系统的初值条件而获得理想系统响应的运用。

转子−轴承系统；滑动轴承；转子动力学；碰摩；吸引域

随着我国高速列车的快速发展，旋转设备正不断朝着高速化、精密化的方向发展，要求转定子之间的间隙越来越小，这使得碰摩成为了转子研究的热点问题[1]，国内外学者针对转子碰摩课题已经做了大量基础性研究，取得了一系列的研究成果。WANG等[2−3]以油膜轴承支撑的Jeffcott 转子为研究对象，分别在对称和非对称油膜力下研究了碰摩转子动力学行为的影响，结果表明在非对称油膜力作用下，系统响应的混沌区域明显更宽，且混沌运动的演化规律将更加复杂。李同杰等[4]考虑齿轮副齿侧间隙以及滑动轴承的油膜力建立了滑动轴承−双转子−齿轮耦合系统的非线性动力学模型，研究发现滑动轴承的油膜对系统的混沌运动具有镇定作用，滑动轴承间隙和转子质量偏心如果设计不当会导致系统齿轮副产生单边冲击现象。目前转子系统的全局动力学分析方法可以分为解析方法和数值方法。其中对于解析方法比较著名的有Melnikov方法，JIANG[5]以一个含碰摩故障的Jeffcott转子系统模型为研究对象，提出了首先分段对系统各段方程的典型解及其稳态解和存在区域进行分析，然后在参数空间中将所得的稳态响应区域进行“拼装”而得到其共存特性的研究方法。但是转子系统属于强非线性系统，其故障类型多、求解难度大，目前尚未有统一的解析求解方法。而数值方法由于具有更强大的直观性和适用性，一直是转子系统全局动力学分析的研究重点。数值方法主要包括直接模拟法(点映射法)和胞映射法[6]，但点映射法需计算很长的时间才能得到系统中的全局动力学特性，而且计算精度低，因此亟需一些高效的数值方法来研究转子系统的全局动力学特性，而胞映射方法就是一种有效的分析转子系统全局动力学特性的方法。胞映射方法最先由Hsu[7]在20世纪80 年代初提出，但应用在较高维动力系统时，“胞”的数量非常大，占用内存空间大，计算速度慢。为此Levitas等[8−9]引入空间Poincaré截面映射，通过在状态空间的定相位面中形成胞空间，并在此空间运用简单胞映射方法对原动力系统进行研究，发展出了Poincaré型的简单胞映射法。周杜等[10]利用简单胞映射方法对一两自由度齿轮进行全局动力学分析，研究发现系统随着激振频率的变化存在多个周期运动共存以及周期运动与混沌运动共存现象。饶晓波[11]应用GPU并行计算方法，研究了碰摩转子系统在故障参数平面中的动力学行为及其参数关联关系，并利用简单胞映射方法探究了系统多吸引子共存现象。本文建立了一个非线性油膜力支撑含碰摩故障的单盘转子−滑动轴承耦合系统动力学模型，采用四阶变步长的龙格−库塔−基尔法对系统的分岔和混沌等非线性动力学行为进行研究，并利用Poincaré型的简单胞映射法分析转速对转子系统的全局动力学的影响，通过合理控制系统的初值条件而获得良好的系统响应，为转子的优化设计和良好运行奠定了基础。

1 系统的动力学模型

图1所示为含有碰摩故障的简化对称刚性支承转子—轴承系统模型示意图，其中，转子的两端的处和处采用对称结构的滑动轴承支撑，转子在轴承处的集中质量为1，在转盘处的集中质量为2，1和2分别为转子在转盘处和转子在轴承处的阻尼；

图1 转子系统动力学模型

1，2和3分别为轴瓦几何中心、转子几何中心和转子质心，1为转盘的质量偏心距；为转盘和定子之间的间隙；假设轴段为无质量的弹性轴段，为弹性刚度，k为定子径向碰摩刚度。

1.1 碰摩力

图2所示为碰摩示意图。图2中，为摩擦点法向与轴方向的夹角；为转子转盘中心的径向位移；P和P分别为法向碰摩力和切向摩擦力。

当大于等于时(即≥)，系统发生碰摩，此时P和P可以表示为：

假设摩擦符合库伦摩擦定律，将碰摩力分解到直角坐标系轴方向和轴方向，可以得到碰摩力在轴方向和轴方向的分量P和P，即：

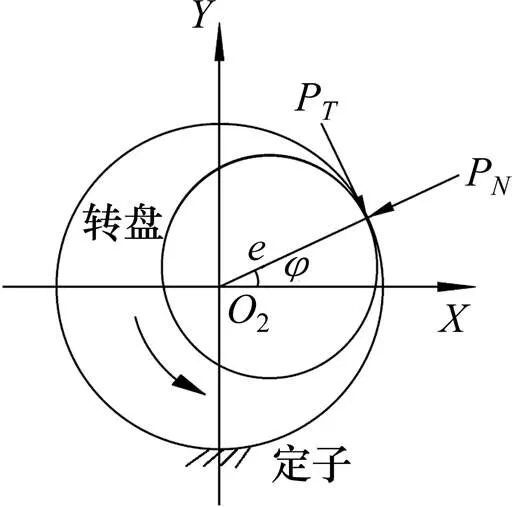
图2 碰摩示意图

1.2 油膜力

本文所研究的转子系统轴承的油膜力模型采用Capone短轴承油膜力模型[12]，该模型计算精度高且收敛性好。油膜压力满足雷洛方程：

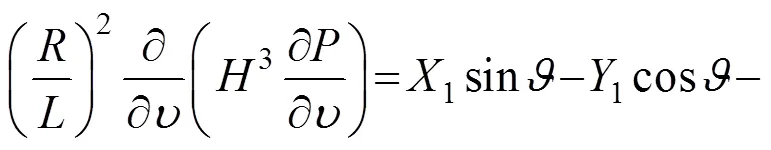
根据式(3)可得油膜压力：

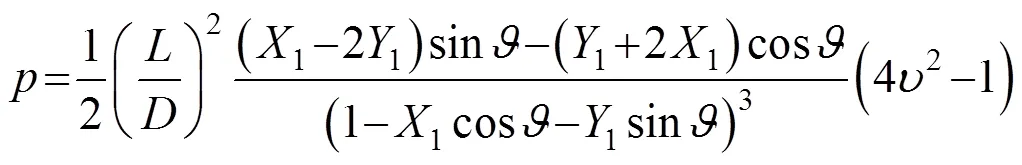
油膜力在和轴上的分量为：

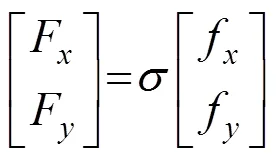
式中：为Sommerfeld修正系数。

其余各参数为：

其中：为润滑油黏度；为轴承宽度；为轴承直径；为油膜间隙；sign()为符号函数；1和1分别为轴承的轴瓦几何中心在轴方向和轴方向的径向位移。

1.3 系统的运动微分方程

引入无量纲量变换：=，x=X/，y=Y/，(=1,2)；其中，为转子角速度。根据转子动力学理论可建立系统的运动微分方程为：

式中：为重力加速度；F, F分别为轴承油膜力在轴方向、轴方向的分量，可参照式(5)。P,P分别为转子系统碰摩力在轴方向、轴方向的分量，可参照式(2)。

2 Poincaré型的简单胞映射

简单胞映射(SCM)方法的基本思想是将维连续的状态空间R离散化为有限个小的几何体(胞)，状态空间离散化而建立胞空间，而Poincaré型的简单胞映射(PCM)方法[13]是在状态空间的定相位面中形成胞空间，利用Poincaré映射将系统进一步转换为Poincaré截面上的点映射系统。采用Poincaré型的简单胞映射(PCM)方法，能够揭示非线性系统在状态空间各共存吸引子的吸引域存在范围，以及参数平面上吸引域拓扑结构的变换规律。对于深入研究系统的全局动力学特性，为系统的结构优化和控制提供理论依据具有重要意义。

3 系统的分岔及混沌分析

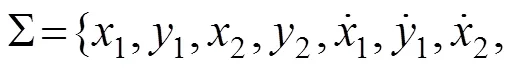
图3呈现了系统转盘在轴方向的无量纲位移随转子转速变化(200～3 000 rad/s)的分岔图，揭示了系统丰富的动力学特性。如图3所示，随着转子转速的增加，系统经历了拟周期运动、单周期运动、多周期运动和混沌运动。当=839 rad/s时，系统发生跳跃，由原来的P-1(P表示周期)运动跳变为P-2运动，此时系统存在P-1运动吸引域和P-2吸引域共存现象。当转速增加到=1 246 rad/s时，系统经周期倍化分岔由P-2运动转迁为P-4运动，随之又跳变到P-3运动，在此转速区域附近系统存在3种运动吸引域的共存现象。转速增加到=1 900 rad/s时，系统再次发生跳变，由P-3运动跳变到P-4运动，并随着转速持续递增发生倍周期分岔，由P-4运动转迁为P-8运动。转速增加到=1 972 rad/s时，系统经逆周期倍化分岔退化为P-4运动。转速继续递增至=2 354 rad/s时，系统由P-4运动经瞬态混沌运动过渡到P-5运动，此后随着转速递增，系统存在P-5运动吸引域和P-chaos(混沌运动)吸引域共存现象。当转速增加到=2 580 rad/s后，系统进入P-chaos运动，并随着转速的继续增加一直维持在混沌运动状态。

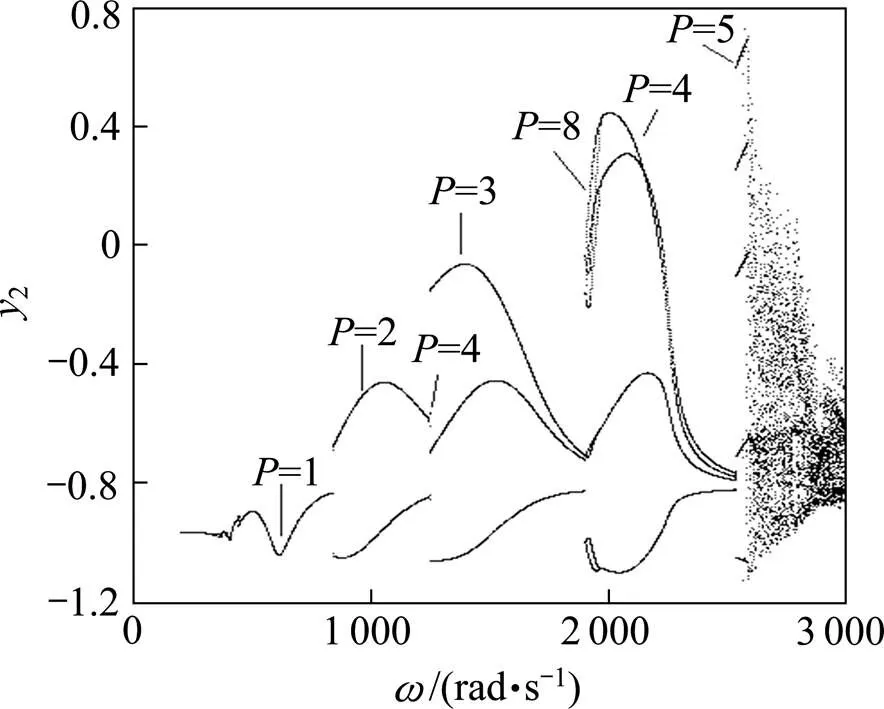
图3 系统的全局分岔图

4 系统的全局动力学分析

4.1 系统在σp相平面的全局动力学分析

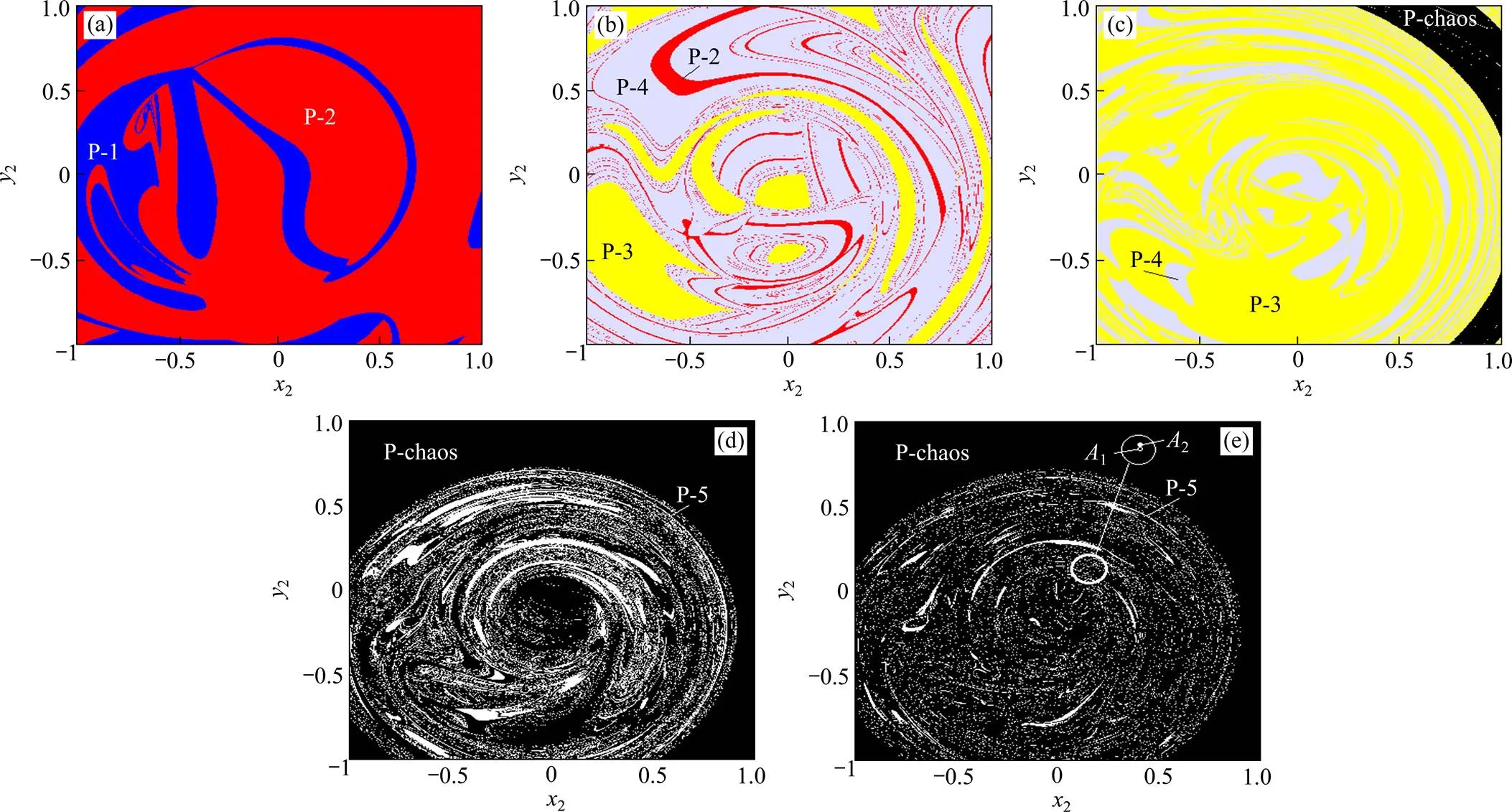
在相平面σ中，为了使研究范围竟可能较广，同时减小初始位置即发生碰摩的情况。取感兴趣的位移初态域：σ={(2,2)∈2|−1.0≤2≤1.0,−1.0≤2≤1.0}，将初态域划分为400×400个状态胞，对相平面σ进行胞映射。系统在σ相平面随转速变化的全局吸引域如图4所示，其中不同颜色表示不同的吸引域。图4(a)为转速839 rad/s时系统的吸引域，其中深色区域代表P-1运动吸引域，浅色区域代表P-2运动吸引域，由图可知深色面积区域大于浅色面积区域，此时P-1运动局部稳定性大于P-2运动。当转速增加到=1 246 rad/s时系统的吸引域如图4(b)所示，此时系统存在P-2运动吸引域、P-3运动吸引域和P-4运动吸引域共存现象，其中浅色P-3运动吸引域和灰色P-4运动吸引域占据了绝大部分面积。带状深色P-2运动吸引域镶嵌在灰色P-4运动吸引域中，这表示系统发生了倍周期分岔，由P-2运动倍化到了P-4运动。转速增加到= 1 900 rad/s时P-2运动消失，此时系统的吸引域如图4(c)所示，只存在浅色的P-3运动吸引域和深色P-4运动吸引域，并且P-3运动局部稳定性大于P-4运动。当转速增加到=2 534 rad/s时的吸引域如图4(d)所示，P-chaos运动和P-5运动在系统中共存，白色的带环状P-5运动吸引域嵌套在黑色的P-chaos运动吸引域中，此时P-5运动对初值非常敏感，极其容易失稳而进入P-chaos运动。转速继续增加到=2 575 rad/s时，系统的吸引域如图4(e)所示，环带状的P-5运动吸引域被P-chaos运动吸引域逐渐吞噬，并形成P-5运动吸引域岛，P-5运动稳定性进一步降低，随着转速的继续增加系统将向P-chaos运动过渡。

(a) ω=839 rad/s；(b) ω=1 246 rad/s；(c) ω=1 900 rad/s；(d) ω=2 534 rad/s；(e) ω=2 575 rad/s

4.2 系统在σq相平面的全局动力学分析

在相平面σ中，取感兴趣的速度初态域：，将初态域划分为400×400个状态胞，对相平面σ进行胞映射。系统在σ相平面随转速变化的全局吸引域如图5所示，其中不同颜色表代表的吸引域与在σ相平面一致。图5(a)为转速839rad/s时系统的吸引域，与在σ相平面相比，浅色区域代表的P-2运动吸引域面积超过深色区域代表的P-1运动吸引域面积，这表示此时在σ相平面，系统的P-2运动的局部稳定性将超过P-1运动。当转速增加到=1 246 rad/s时系统的吸引域如图5(b)所示，与在σ相平面相比，大部分浅色的P-3运动吸引域被灰色的P-4运动吸引域吞噬。转速增加到=1 900 rad/s时，此时系统的吸引域如图5(c)所示，与在σ相平面相比，增加了黑色的P-chaos运动吸引域。这表示与在σ相平面相比，速度对系统的稳定性影响更大，在系统转盘转速接近1的区域，为维持系统的稳定性可以调节系统转盘转速的初值以避开P-chaos运动吸引域区域。当转速增加到= 2 534 rad/s时的吸引域如图5(d)所示，与在σ相平面相比，白色的P-5运动吸引域面积被压缩到相平面的左下角与黑色的P-chaos运动吸引域面积交织呈一圆盘状。转速继续增加到=2 575 rad/s时，系统的吸引域如图5(e)所示，P-5运动吸引域面积被P-chaos运动吸引域逐渐吞噬，呈散状分布于P-chaos运动吸引域面积中。

(a) ω=839 rad/s；(b) ω=1 246 rad/s；(c) ω=1 900 rad/s；(d) ω=2 534 rad/s；(e) ω=2 575 rad/s

(a) Poincaré截面图；(b) 轴心轨迹图

5 应用举例

(a) Poincaré截面图；(b) 轴心轨迹图

6 结论

1) 建立了一个非线性油膜力支撑含碰摩故障的单盘转子−滑动轴承系统动力学模型，利用Poincaré型的简单胞映射方法研究了转子系统的全局动力学特性，发现系统存在单周期运动与多周期运动共存，多周期运动与多周期运动共存，以及多周期运动与混沌运动共存。

2) 分析了系统在2个感兴趣相平面内各种运动吸引域的位置，并通过应用举例说明，在系统理想运动的吸引域范围内选择系统的初值条件，可以获得理想的系统响应。这为转子系统的动力学优化设计提供了理论基础，对于在不良参数区域改善转子系统的动力学特性有着重要的工程意义。

[1] 马辉, 李焕军, 刘杨, 等. 转子系统耦合故障研究进展与展望[J]. 振动与冲击, 2012, 31(17): 1−11. MA Hui, LI Huanjun, LIU Yang, et al. Review and prospect for research of coupling faults in rotor systems [J]. Journal of Vibration and Shock. 2012, 31(17): 1−11.

[2] WANG Junguo, ZHOU Jianzhong, DONG Dawei, et al. Nonlinear dynamic analysis of a rub-impact rotor supported by oil film bearings[J]. Archive of Applied Mechanics, 2013, 83(3): 413−430.

[3] CAI D, XIAO H. Dynamic modeling and analysis of sliding bearing-rotor system with coupling rubbing faults [C]// 2016 Sixth International Conference on Instrumentation & Measurement, Computer, Communication and Control (IMCCC). IEEE, 2016: 163−166.

[4] 李同杰, 靳广虎, 朱如鹏, 等. 滑动轴承支撑下齿轮耦合转子系统弯扭耦合振动特性分析[J]. 中南大学学报(自然科学版), 2018, 49(3): 566−573. LI Tongjie, JIN Guanghu, ZHU Rupeng, et al. Nonlinear bending-torsional dynamics of geared rotor system supported by sliding bearing[J]. Journal of Central South University (Science and Technology), 2018, 49(3): 566− 573.

[5] JIANG J. Determination of the global responses characteristics of a piecewise smooth dynamical system with contact[J]. Nonlinear Dynamics, 2009, 57(3): 351− 361.

[6] 尹磊磊. 典型非光滑动力学系统分岔与多解共存现象研究[D]. 长沙: 湖南大学, 2014: 25−42. YIN Leilei. Research on the global bifurcations and coexistence of multiple solutions in typical non-smooth dynamical systems[D]. Changsha: Hunan University, 2014: 25−42.

[7] Hsu C S. A theory of cell-to-cell mapping dynamical systems[J]. Journal of Applied Mechanics, 1980, 47(4): 931−939.

[8] Levitas J, Weller T, Singer J. Poincare-like simple cell mapping for non-linear dynamical systems[J]. Journal of Sound and Vibration, 1994, 176(5): 641−662.

[9] Levitas J, Weller T. Poincare linear interpolated cell mapping: Method for global analysis of oscillating systems[J]. Journal of Applied Mechanics, 1995, 62(2): 489−495.

[10] 周杜, 乐源, 李高磊, 等. 两自由度齿轮传动系统全局动力学研究[J]. 动力学与控制学报, 2019, 17(6): 514− 519. ZHOU Du, YUE Yuan, LI Gaolei, et al. Study on global dynamic characteristic of two-degrees-of-freedom gear transmission system[J]. Journal of Dynamics and Control, 2019, 17(6): 514−519.

[11] 饶晓波. 基于GPU并行计算的旋转机械系统动力学参数关联关系研究[D]. 兰州: 兰州交通大学, 2018: 129− 141. RAO Xiaobo. The study of parameters incidence relation about the dynamics inrotary machine system based on the GPU parallel computation[D]. Lanzhou: Lanzhou Jiaotong University, 2018: 129−141.

[12] Adiletta G, Guido A R, Rossi C. Chaotic motions of a rigid rotor in short journal bearings[J]. Nonlinear Dynamics, 1996, 10(3): 251−269.

[13] 刘恒, 虞烈, 谢友柏, 等. 非线性不平衡轴承转子系统全局特性及其稳定性准则的研究[J]. 机械工程学报, 1999, 35(2): 62−66.

LIU Heng, YU Lie, XIE Youbai, et al. Research of global characteristic and stability rule of nonlinear unbalanced bearing rotor systems[J].Journal of Mechanical Engineering, 1999, 35(2): 62−66.

[14] 曹素兵. 转子系统碰摩的非线性行为研究[D]. 自贡: 四川理工学院, 2008: 26−72. CAO Subing. Study on nonlinear behavior of a contact- rubbing Jeffcott rotor system[D]. Zigong: Sichuan University of Science & Engineering, 2008: 26−72.

Study on global dynamic characteristic of rubbing rotor—oil film bearing system

ZENG Xuyan1, 2, SHI Yuqing1, 2, LIU Jun1, 2, GUO Yao3

(1. School of Mechanical Engineering, Lanzhou Jiaotong University, Lanzhou 730070, China;2. Gansu Provincial Key Laboratory of System Dynamics and Reliability of Rail Transport Equipment, Lanzhou 730070, China;3. College of Computer and Information Engineering, Hunan University of Technology and Business, Changsha 410205, China)

A dynamic model of the coupling system of single-disk rotor and sliding bearing including rub-impact fault was established, which considered the non-linear oil film force of the sliding bearing and the rubbing force of the rotor and stator. The fourth-order Runge-Kutta-Gill method with varying steps was used to solve the dynamic equation and obtain the model’s vibration response, and the global dynamics analysis of the rotor system was performed by using a simple cell mapping method of Poincaré type. The results show that: With the increase of the rotation speed, there are multiple periodic solutions coexisting and periodic solutions coexisting with chaotic motion. Finally, the application of the ideal system response is obtained by reasonably controlling the initial value conditions of the rotor system under the condition of bad parameters.

rotor-bearing system; sliding bearing; rotordynamics; rub-impact; domain of attraction

O322；TH133

A

1672 − 7029(2021)02 − 0494 − 08

10.19713/j.cnki.43−1423/u.T20200387

2020−05−11

兰州交通大学青年科学研究基金项目(2015019)

侍玉青(1988−)，女，甘肃民勤人，副教授，博士，从事非线性动力学及控制研究；E−mail：shiyq@mail.lzjtu.cn

(编辑 阳丽霞)