移动群智感知下的交通流速缺失数据恢复算法

张建宗，陶 丹

(北京交通大学 电子信息工程学院信息处理与人工智能研究所，北京100044)

1 引 言

随着社会的发展，机动车数量逐年增加，交通拥堵问题成为现代城市面临的主要问题.为了减轻城市路网的压力，对交通状态进行有效的评估显得尤为重要.近年来，我国大中城市在主要道路布置了大量交通传感器(比如：摄像机、环路感应器)进行交通状态监测，但这种方式部署困难且维护成本较高.随着移动终端处理器、内存等硬件设备的快速发展和提升，摄像头、麦克风、GPS、陀螺仪、加速度计等传感器嵌入到以智能手机、平板电脑为代表的移动智能终端中.在此背景下，人们提出了一种新型的感知模式——移动群智感知[1]，即利用城市中广泛存在的移动智能设备以及车辆，通过群体间有意识或者无意识的协作完成感知任务.由于移动群智感知模式下的感知节点分布广泛、移动灵活，因此被广泛应用在智能交通领域[2].其中，利用探测车数据进行城市规模的交通状态评估就是较为常见的一种应用[3].探测车是安装有GPS等信息采集设备的车辆，能够周期性的将车辆位置以及行驶状态上传至控制中心，基于此，能够利用某时间段内路段上的流速来表征交通状况.由于探测车在城市范围内的概率分布，因此当探测车数量足够大时，使得城市级的交通状态评估成为可能.另外，安装在探测车上的GPS设备的普及也极大的降低了系统成本.然而，受到探测车规模的限制，导致车辆在时空上分布不均匀，此时在使用探测车数据进行交通状态评估时存在着数据缺失，这是其应用于交通状态评估时的主要困难之一[4].

为实现对城市级交通状态的有效评估，得到完整的城市交通状态地图，需要对缺失的交通数据进行准确恢复.近年来积累了一系列利用探测车评估交通状况的研究成果.基于公交车数据，Herring等[5]提出了一种概率模型框架来预测主干道的行程时间分布，将交通状态建模为耦合隐马尔可夫模型以估计模型参数.然而，这种方法需要通过现场研究和大量探测数据进行训练.Zhu等[4]将出租车作为路况感知的探测车辆，随后分析路况数据在时空上的结构性特点，利用低秩矩阵填充技术推测出没有探测车经过的路段的路况信息，以此实现大范围的路况评估；然而该方法在数据缺失程度较大时数据恢复的效果不太理想.随着机器学习的发展，更多研究学者尝试学习数据特征以实现数据恢复.Zhang等[6]将图像超分辨率的概念应用于交通流量数据感知重建.Zhang等[7]利用卷积神经网络模型学习出租车交通流模式，进而预测下一时刻的交通流分布矩阵，然而，这些重建过程都是“网格化”分布节点的数据采样过程，与群智感知网络节点非均匀感知过程不尽相同.由此，本文研究利用有限探测车数据进行城市级交通状态评估，针对路网提取、交通流速矩阵获取以及缺失数据恢复等开展了一系列研究工作.

2 交通流速缺失数据恢复框架

如图1所示，为了实现城市级交通状态评估，本文提出了交通流速缺失数据恢复框架.探测车会实时的向接收中心发送其运行状态以及位置信息，本文以某一时段内某一路段的探测车速度表征交通运行状况.首先对数据进行预处理，删除冗余数据并清理停滞点，其次根据GPS数据获取道路中心点完成路网提取，再次对其进行时空划分，并计算细粒度下的交通流速，进而得到表征交通状况的交通流速矩阵.在此基础上，本文充分考虑数据间的时空相关性，改进压缩感知稀疏基进而完成交通缺失数据恢复，达到路况评估的目的.

图1 交通流速缺失数据恢复框架Fig.1 Traffic velocity missing data recovery framework

2.1 数据预处理

同一辆探测车在行驶过程中，GPS终端会周期性地将GPS数据发送到控制中心.由于设备或者噪声等影响而产生的错误数据会直接影响路网提取的精度，进而影响后续的交通状态评估.数据预处理是路网提取的前提，主要包括清除冗余数据与消除停滞点两方面.

2.1.1 清除冗余数据

由于数据传输误差，会造成越界数据的存在，常见的如车头方向超出[0°，359°]，或者GPS点超出研究地图的经纬度范围，对此类数据设置阈值范围进行清理.此外，数据中存在全部字段值均相同的情况，清除掉这些冗余的定位数据，以提升路网提取的效率.

2.1.2 消除停滞点

由于本文将出租车作为探测车进行研究，分析出租车运营特性可知，车辆在商场、车站等地常常停滞待客，或是乘客上下车也会造成数据变化微小，通常此类停滞点数据在整体数据中占比较大，且无法提供有效的路况信息，应当删除此类数据.同时，考虑到道路交叉口信号灯变化周期等情况，本文将连续5分钟车速为0的数据当成停滞点进行清除.

表1为部分预处理后的数据示例，经过数据预处理后，数据剔除率高达55.67%.

表1 部分预处理后数据示例Table 1 Samples of partial preprocessed data

2.2 路网提取

在城市交通地图中，由于探测车一般分布在道路上，而其他地方的探测车数据分布量较小，因此可以将研究区域划分为网格，并计算网格内探测车密度，设置合理的阈值筛选出作为道路主干道的网格，并拟合形成路网，以此达到路网提取的目的.这种基于探测车数据的路网提取方法不仅可以对现有的道路网络进行修正，还为后续的交通流速计算提供了基础.本文将路网提取分为道路中心点提取和道路中心点拟合两步.

2.2.1 道路中心点提取

基于网格思想，考虑到经纬度与现实距离的换算关系，同时考虑道路实际宽度，将GPS数据在空间维度以2×10-5°(约为2米)为边长进行网格划分，这样能保证较小的运算复杂度同时在形成路网时误差较小.

设定网格内轨迹点密度阈值Q1、邻域内网格数目阈值Q2和聚类半径E，当网格密度大于密度阈值Q1时则将此网格判定为路网网格，如果某路网网格E邻域内的总路网网格数量大于Q2，则通过聚类算法将E邻域内包含的网格转化为聚类点，聚类点坐标由邻域内所有路网网格决定.

2.2.2 道路中心点拟合

由于城市道路复杂多变，故本文采用了准均匀B样条曲线拟合方法，该方法能够在拟合过程中将首尾端点拟合到曲线上，得到实际路网形状的曲线.基于网格密度的路网获取如算法1所示.

算法1.基于网格密度的路网获取算法

输入：GPS数据集合I{p1，p2，…，pn}，密度阈值Q1、Q2和聚类半径E.

输出：路网矩阵R

1.以2×10-5°进行网格划分，得到网格矩阵N；

2.for网格矩阵中每个位置Nij；

3. 计算网格内GPS数据密度K；

4. 如果K大于Q1，则形成新的集合C，并计算坐标值；

5.end for；

6.return聚类点集合C={C1，C2，…，Cn}；

7.for聚类点集合C中每个网格Cij；

8. 计算网格质心坐标；

9.end for；

10.return网格质心坐标集合D={D1，D2，…，Dn}；

11.对集合D进行准均匀B样条曲线拟合；

12.return路网数据R

进行路网提取前后的对比效果如图2(a)、图2(b)所示.由图可以得出：通过筛选网格密度过低的网格，可以有效地清除主干道路以外的数据点和人迹罕至的小路数据，且道路形状保存较好.

图2 路网提取前后对比Fig.2 Comparison before and after road network extraction

2.3 时空划分

1)时间划分：由于城市道路状态在时间上变化频繁，因此在对道路进行状态评估时需要将其划分为一定的时间粒度进行研究.图3分别是以5分钟、10分钟和15分钟为时间粒度下的数据缺失情况.由图可知：虽然进行时间划分时时段越长数据缺失率越小，但过长的时间间隔不能及时反映交通状况的变化.因此考虑到路况变化周期，本文选取5分钟作为时间粒度.将一天时间划分为288(12×24)个时间片段，在以5分钟为时间粒度时，数据缺失率高达85.3%.

图3 不同时间粒度下数据缺失率Fig.3 Comparison ofthe levels of data missing at different time granularities

2)空间划分：对于一条道路来说，尤其对于距离过长、交通状态差别或变动较大的路段，难以用一个流速表征整条路段的信息.为此，本文将道路划分为若干个子路段，用子路段的流速能够更好地表示道路的交通状态.

考虑到城市路网中各道路被交叉口自然分割，形成存在一定拓扑结构的路段，本文将道路交叉口作为路段划分的自然分界点.对于长度大于0.5km的自然路段，利用公式(1)对其进一步划分为若干子路段，

n=(⎣L」+1)×2

(1)

其中，n为某一路段被划分的个数，L为路段长度，单位km.经过子路段划分后过长的路段被划分为长度在0.25～0.5km之间的子路段.

经过路段划分，将研究区域内的路网划分为了432个路段.由此完成了数据的时空划分.

2.4 流速计算

通常车辆在道路上的行驶速度能够直接反映道路的通行状况，因此本文将路段内车辆流速作为评价交通状态的指标.通常人们在计算交通流速时是通过计算某一路段内经过车辆的速度的平均值或是通过车辆的行驶轨迹与时间估计流速，但这种方法在样本极差较大时或是车辆数目较少时会带来较大的误差.因此本文区分两种典型情形并设计了一种自适应的流速估计方法.

1)样本数大于δ且极差大于μ，此时说明该路段内通过的车辆较多，但不同车辆间车速有着较大的差异.因此根据样本数据的奇偶性，利用公式(2)计算该路段内的流速的中位值.式中v为路段内流速，un为第n个车速数据.

(2)

2)样本数小于δ或者样本数大于δ且极差小于μ，此时说明了该路段内通过的车辆较少，或是车辆较多且不同车辆间的车速差别不大，使用公式(3)计算该路段内的流速.

(3)

自适应的流速估计方法采用均值计算的思想，设置参数在数据满足一定条件下使用中位值法以避免离群点的影响.本文随机节选8个路段计算其流速，图4为不同流速计算方法的结果对比.相比传统平均值法、中位值法，本文设计的流速计算方法更接近准确值，为后续的交通状态评估奠定了坚实的基础.

图4 不同流速计算方法的对比Fig.4 Comparison of different velocity calculation methods

通过数据预处理、路网提取、时空划分以及流速计算等一系列处理，得到了存在缺失的交通流速矩阵.交通流速矩阵示例如表2所示.这样，可以将探测车数据转化为交通流速矩阵，矩阵的行列对应着路网的路段和时段，由此可以更加方便地进行时空建模和数据恢复.

表2 交通流速矩阵示例Table 2 Sample of traffic velocity matrix

3 基于时空相关性的压缩感知数据恢复算法

皮尔逊相关系数是刻画变量之间关联性常用的参数，因此本文选取皮尔逊相关系数来揭示交通流速数据间的时空关联，对于二维向量存在：

(4)

实验选取了同一路段相邻7个时间片段和同一时段相邻的7个路段分别计算其相关系数，结果如图5(a)、图5(b)所示.分析图中数据可知：编号越接近的时段或路段其皮尔逊系数越大，路段(时段)间隔小于3时系数基本都在0.8以上，数据间有着强烈的时空关联性.

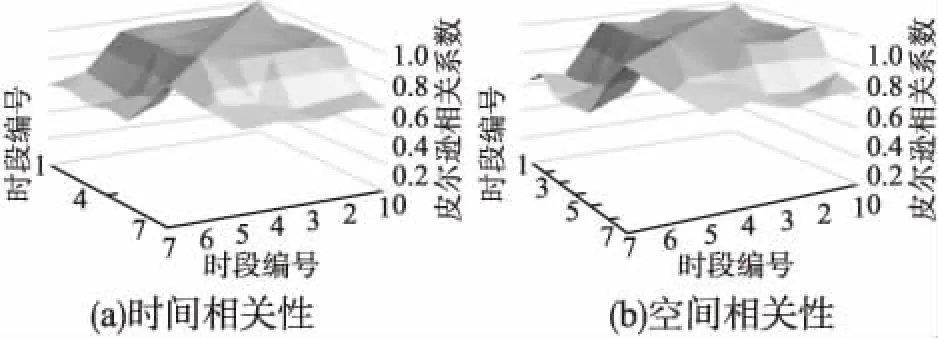
图5 时空相关性Fig.5 Spatio-temporal correlation

由于探测车数量有限，对数据进行时空划分后使得数据存在大量的缺失.近年来对探测车进行交通数据恢复时通常认为数据缺失是无规律的，然而通过分析上一章节得到的流速矩阵发现：矩阵中数据缺失存在着一定的规律.根据缺失数据的位置特点，将数据缺失情形分为以下3种：

1)随机缺失：交通流速缺失元素随机的分布在矩阵的各个位置.如果缺失的数据在流速矩阵中表现为分散的维度小于等于3(例如1×3、2×1)的行列矩阵，则将此类情形归为随机缺失.产生这种情况的原因可能是不同时段不同路段探测车的概率分布所致.

2)整块缺失：交通流速缺失数据导致流速矩阵中出现大块的空白情况，即缺失数据在流速矩阵中呈现为行列皆大于2(例如3×3、3×4)的子矩阵，则此类情况为整块缺失.产生此情况的原因可能是某一区域探测车长时间未覆盖.

3)行列缺失：交通流速矩阵中某行或某列数据连续缺失，表现为元素大于3的行矩阵或者列矩阵(例如4×1、1×5)，则此类情况为行列缺失.产生这种情况的原因可能是连续一段时间内没有探测车经过或是一段道路长时间未被探测车覆盖.

特别地，一些特殊情形可以划分为3种缺失情形的组合，不再赘述.

本文改进了压缩感知算法的稀疏基，以避免大范围数据缺失带来的影响，将缺失数据的预测问题建模成稀疏向量的恢复问题.在此，设计了一种基于时空相关性的压缩感知数据恢复算法STC-CS(Spatio-Temporal Correlation based Compressed Sensing).

交通流速往往在时间上平滑变化，即在两个相邻的时间粒度下交通流速值变化较小，因此设计时间稀疏基矩阵T：

(5)

则流速si在矩阵T下的投影为γt=Tsi，令φt=T-1，则流速可以稀疏表示为si=φtγt.

由于城市路网之间往往存在着一定的拓扑结构，这种拓扑结构揭示了数据间的空间相关性，因此设计空间稀疏基矩阵：

(6)

由上所述，分别从时空两个角度考虑设计了稀疏表示基，将其进行Kronecker积运算就可以得到交通流速的稀疏表示基：

φ=φt⊗H

(7)

则交通流速矩阵可以进行稀疏表示为：

si=φα

(8)

假设带有缺失的流速矩阵为si，定义矩阵W∈Rm×n表示S中是否缺失

(9)

假设完整的流速数据为S，则：

si=S⊙W

(10)

由上述公式可知，矩阵W的第i行表示时间序列中的数据是否缺失，而缺失数据的预测就是利用未缺失的数据作为测量值恢复原数据.由此设计观测矩阵：

(11)

如果矩阵ψi∈RMi×K在(m，n)处的值为1，表明第m个测量值是在第n个时段得到的.就可以得到观测矩阵：

(12)

令y表示si的观测值，则矩阵si观测向量可表示为：

y=ψφα

(13)

已知y、ψ、φ，就可以通过求解凸优化问题求解α，进而恢复交通流速数据.

4 实验仿真

本文基于移动群智感知思想，使用探测车数据进行路况评估.数据来源为东莞市1000辆出租车采集的约25万条数据(1)OpenData2[EB/OL].http：//www.openits.cn/openData2/604.jhtml.，时间跨度为10天，覆盖范围为经度23.0°～23.07°E，纬度113.7°～113.84°N，每条探测车数据包含车辆编号、位置、时间、车辆速度以及车头方向等信息.

本文设计了两组对比实验：随机缺失情形下不同数据缺失程度对比与50%数据缺失程度下不同缺失情形对比.实验与3D形函数时空插值修复法(3D-SHAPE)[8]、基于灰色GM(1，N)模型[9]、基于统计学的插值计算法(SI)以及最近邻算法(KNN)这4种方法进行对比.其中，3D-SHAPE是将数据的时空相关性加入到3D函数中进行数据恢复.基于灰色GM(1，N)模型是基于灰色残差GM(1，N)模型的数据修复算法.SI与KNN是依据相邻数据间关系进行数据恢复.

为了比较以上方法在本文实验数据集下的恢复结果，本文采用均方根误差(RMSE)、均绝对误差(MAE)、平均绝对值误差率(MAPE)作为性能评价标准.

1)随机缺失情形下的数据恢复效果

为了比较随机缺失情形下不同数据缺失程度的数据恢复性能，本文选取了数据缺失程度分别为30%、50%和80%的数据，并使用上述5种算法对缺失数据进行恢复.数据恢复性能如表3所示.

表3 不同缺失程度下数据恢复性能对比Table 3 Comparison of data recovery performances at different evels of data missing

分析可知：当数据缺失程度较小时，由于未缺失数据能够提供较多的信息，因此5种数据恢复算法都能够较为准确的恢复缺失数据.其中SI算法和KNN算法的恢复效果相较于其他3种算法略差.在数据缺失程度为50%和80%时，SI算法和KNN算法的恢复性能显著下降，而另外3种考虑数据时空特性的数据恢复算法恢复的交通流速数据更加准确，更接近实际中的交通流速数据.在数据缺失程度为50%时，3D-SHAPE算法、GM(1，N)算法和STC-CS算法的MAPE值基本相同，但在MAE与RMSE的表现上各有优势.当数据缺失程度进一步加大时，由于缺乏临近数据的支持，导致SI算法和KNN算法的性能表现变得更差.3D-SHAPE算法与GM(1，N)算法恢复效果略有下降，而本文所提的STC-CS算法由于是基于数据时空特征将数据稀疏表示，重构原始数据进而恢复缺失数据，因此恢复效果优于其他算法，仍然能够较为准确地恢复缺失数据.

2)不同缺失情形下的数据恢复效果

该实验将数据缺失程度统一设定为50%.随机缺失情形下的数据恢复效果与表3(b)实验条件、实验结果相同；整块缺失与行列缺失情形下，块/行列的规模和数目是随机的.表4为5种算法在3种不同缺失情形下的数据恢复效果.

表4 不同缺失情形下的数据恢复性能对比Table 4 Comparison of data recovery performances at different missing cases

通过分析可知：相较于整块缺失与行列缺失，随机缺失下由于缺失数据均匀分布，使得5种数据恢复算法的表现最好.行列缺失情形下本文所提的STC-CS算法的数据恢复效果相较于3D-SHAPE与GM(1，N)性能略优.在整块缺失情形下由于大块数据的缺失使得块中心位置的参考数据变少，导致5种数据恢复算法的误差变大，但相比较而言本文提出的算法恢复效果表现最佳，这是由于STC-CS算法将原始交通流速矩阵映射到其他维度，有效地避免了上述现象.

5 总 结

充分考虑探测车数据的时空特征，本文开展交通流速缺失数据恢复研究.设计了基于网格密度提取路网的方法，提出了自适应的路段流速计算方法，进而得到交通流速矩阵，基于数据时空特征改进了压缩感知的稀疏基实现有效数据恢复.一系列实验验证本文所提方法在缺失程度较大时能够有效地恢复缺失数据.