基于MATLAB一阶微分方程的仿真

任春年 李会荣 魏倩茹

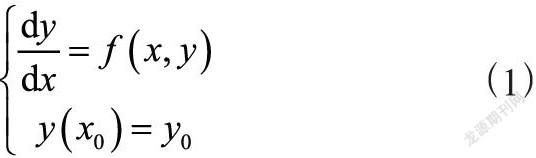
摘  要：为得到更加精确的求解微分方程数值解的方法，采用了显式欧拉法、隐式欧拉法、改进欧拉法以及四阶龙格库塔等方法与MATLAB软件中专有的ode45函数作比较，对用不同方法来求解微分方程的求解结果进行了研究，通过例证以及数据分析，得出在步长h任意时，四阶龙格库塔法的精准度、稳定性都要高于其他三种欧拉法，使在微分方程求解方法的选择上更具针对性。

关键词：微分方程;欧拉法;四阶龙格库塔法

中图分类号：TP391.9               文献标识码：A文章编号：2096-4706（2021）15-0160-03

Abstract： In order to obtain a more accurate numerical solution of differential equations， the explicit Euler method， implicit Euler method， improved Euler method and fourth-order Runge-Kutta method are compared with the special ode45 function of MATLAB software. The results of solving differential equations by different methods are studied. Through examples and data analysis， when the step h is arbitrary， the accuracy and stability of the fourth-order Runge-Kutta method are higher than the other three Euler methods， which makes the choice of differential equation solution method more targeted.

Keywords： differential equation; Euler method; fourth-order Runge-Kutta method

0  引  言

微分方程的理论和方法不仅广泛应用于自然科学，在数学研究领域内，通過深研相关文献可知，关于一阶微分方程的各种边值问题已取得不少的研究成果。文献[1-2]中表示欧拉法解微分方程时过程虽简单，但是误差较大。

本文利用显式欧拉法、隐式欧拉法、改进欧拉法、四阶龙格库塔等方法来对一阶微分方程进行求解，通过对比相关数据，分析以上各种方法求解一阶微分方程的优劣势，进一步提高一阶微分方程的求解效率。

1  常微分方程的基本概念

含有未知函数导数（或微分）的方程，称为微分方程，未知函数是一元函数的微分方程称为常微分方程，未知函数是多元函数的称为偏微分方程[3]。

一阶常微分方程初始问题：

其中x0为初始时间（已知常数），y0为初始状态，函数f（x，y）关于y满足利普希茨条件，保证初值问题解的存在且唯一。

2  欧拉法

欧拉法的主要思想是迭代思想，也就是逐次替代，从而求出所需要的解，而且还要达到一定的精准度。欧拉法分别有显式欧拉法（前向欧拉法）、隐式欧拉法（后向欧拉法）和改进欧拉法。如果微分方程的最本质的特征是方程中含有倒数项，那么数值解首要先消除倒数值，这个过程被称为离散化。

2.1  显式欧拉法

使用一阶前向差商代替微分[4]：

式中，h为时间步长。

微分方程的显式差分方程：

上式是关于y（m）向y（m+1）的递推形式，则可逐步求出y（1），y（2），y（3）…y（n）…，是关于y（m）的一个直接计算公式，既所求出的离散序列为该方程的数值解。

2.2  隐式欧拉法

使用一阶向后差商代替微分[5]：

微分方程的隐式差分方程：

在第m步迭代时，y（m-1），x（m）已知，y（m）为待求未知量，f（x（m），y（m））是关于待求未知量y（m）的函数，则方程是关于y（m）的非线性方程。通过非线性方程的迭代解法求出y（m）。则可逐步求出y（1），y（2），y（3）…y（n）…，所求出的离散序列为方程的数值解。

2.3  改进欧拉法

先用显式欧拉法求解m+1步的预测值：

再用m步微分值f（x（m），y（m））和k+1步预测的微分值f（x（m+1），y（m+1））的平均值来近似微分：

再用显式欧拉法校正k+1步的计算值：

综上所述，改进后的欧拉算法为：

上式就是关于y（m）向y（m+1）的递推形式，根据初始条件按照递推关系依次求出y（1），y（2），y（3）…y（n）…，所求出的离散序列为方程的数值解。

2.4  三种欧拉方法对比

微分方程数值解法的本质特征是使用数值积分实现向y的转换。显式欧拉法和隐式欧拉法都使用的是矩形数值积分方法，是一阶算法，截断误差为O（h2）;改进欧拉法使用的是梯形数值积分方法，是二阶算法，截断误差为O（h3）。

3  四阶龙格库塔法

欧拉法在求解方程时，随着步长的增加，欧拉法一阶算法精度下降很快。而龙格库塔法都是由合适的泰勒方法推导得到，使得误差为O（h5），其求解精度高，且易于编程。

四阶龙格库塔法的求解算法为式（10）所示。

四阶龙格库塔法的算法是关于y（m）向y（m+1）的递推形式，可以根据初始条件按照递推关系依次求出y（1），y（2），y（3）…y（n）…，則离散序列就是方程的数值解。

4  数值实验

4.1  MATLAB中微分方程数值中的函数

在求解微分方程的数值解时，ode是MATLAB软件中专有的求解微分方程的函数。在MATLAB中共有7个函数，分别是：ode45，ode23，ode113，ode15s，ode23s，ode23t和ode23tb。其中ode45采用了四阶-五阶Runge-Kutta算法，用四阶龙格库塔法提供候选解，五阶龙格库塔法控制误差。

4.2  数值举例

例1，求解一阶常微分方程：

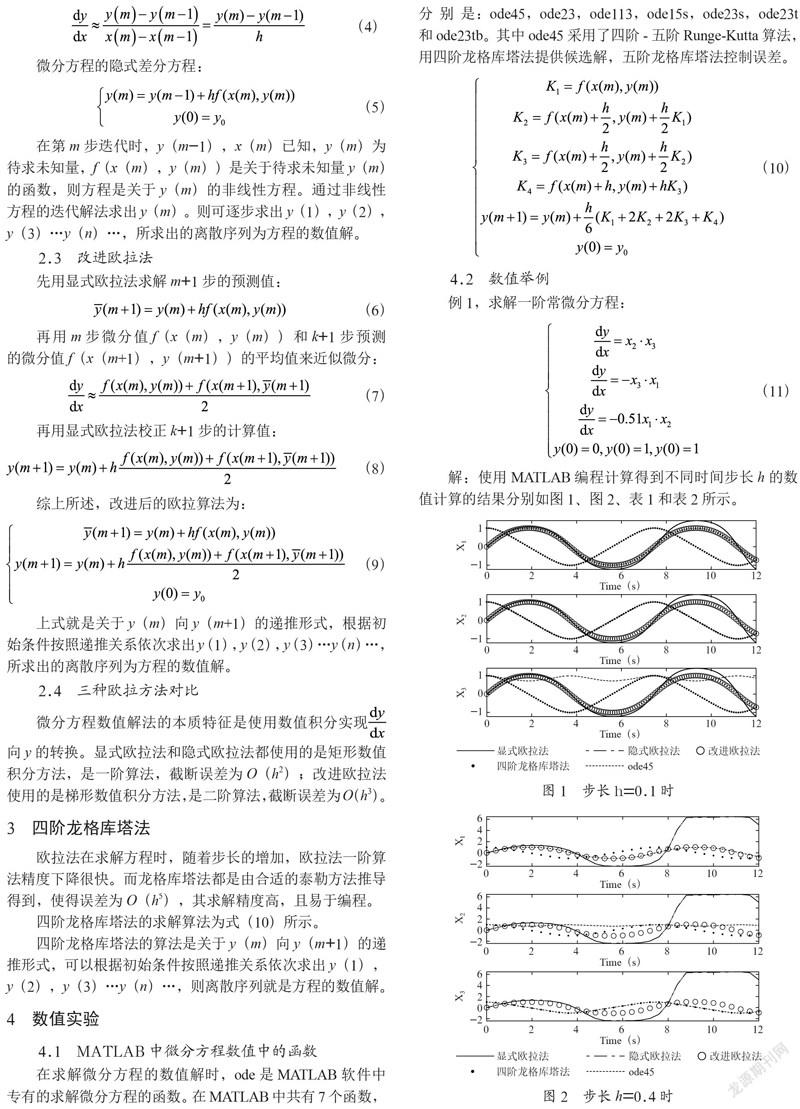
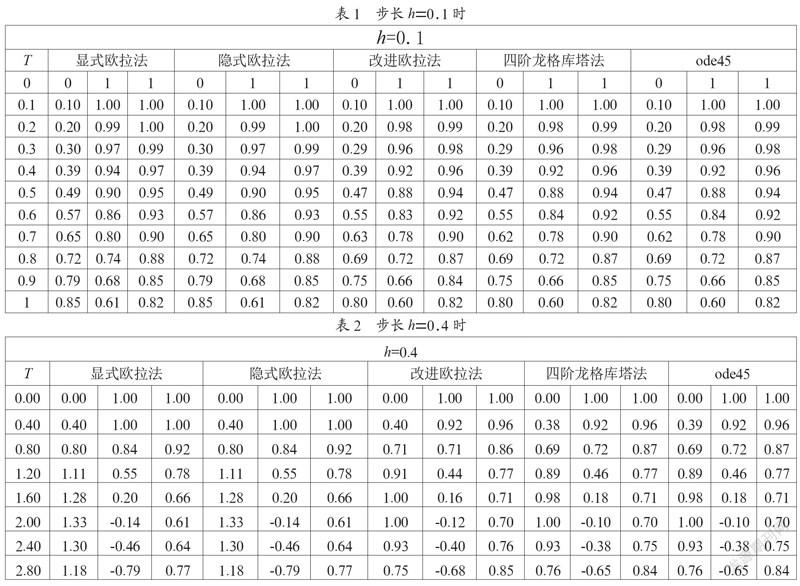
解：使用MATLAB编程计算得到不同时间步长h的数值计算的结果分别如图1、图2、表1和表2所示。

由例题数据分析可得，显式欧拉法计算量小，但精度低;而隐式欧拉法的计算远比显式欧拉法困难，但其计算稳定性好。改进欧拉法的精度高于前两者。

四阶龙格库塔法即使在步长h很大时，求解的精准度比MATLAB自带的ode45函数和改进欧拉法精度明显提高。四阶龙格库塔法相对于使用ode45函数最大的优势在于：可以将求解程序和模型描述文件融合起来，能够解决各类参数时变、多模型切换等问题。

5  结  论

通过上述例子可以直观地看到各种方法在解微分方程数值解时的优缺点，无论是显式、隐式还是改进欧拉法，精准度主要取决于区间的大小和步长h，当取得区间过大时，会出现前一部分区间的近似值偏差小，后一部分的结果偏差值较大。

四阶龙格库塔法比显式欧拉法、隐式欧拉法以及改进欧拉法的精准度更高，与MATLAB软件中的ode45函数相比有着更多的优势。

通过以上对比分析，在求解微分方程的数值解时，可以供读者快速便捷的选取合理的算法应用于计算，使微分方程在对实际问题的研究应用中更加高效快捷。

参考文献：

[1] 姜兆柠.常微分方程数值解的求解 [J].科技经济导刊，2019，27（17）：154-155.

[2] 刘相国，杨晓伟，王冬银.基于MATLAB的《常微分方程》教学研究 [J].西安文理学院学报（自然科学版），2020，23（2）：124-128.

[3] 王高雄，周之铭.常微分方程：第3版 [M].北京：高等教育出版社，2006.

[4] 梁春叶，王桥明，孙远通，等.微分方程数值解之欧拉法在MATLAB下的应用 [J].科技风，2021（10）：71-72.

[5] 贾新辉.基于微分方程模型信赖域子问题的改进欧拉法 [D].太原：太原科技大学，2017.

作者简介：任春年（1999.12—），男，汉族，陕西榆林人，本科在读，研究方向：数学与应用数学。

3780500338226