精确函数在IVIFS多准则决策中的应用

张燕丽, 占玉芬, 黄淑伟

(沈阳师范大学 软件学院, 沈阳 110034)

0 引 言

为处理不精确、不确定信息决策问题,1986年,Atanassov[1]提出了直觉模糊集的概念。1989年,Atanassov等[2]提出了区间直觉模糊集的概念,使隶属度和非隶属度由一个精确数变为区间数,这个概念在处理不确定信息时更为灵活。在实际应用中,这更符合人们的偏好,并且直觉模糊或区间直觉模糊更容易提供信息。因此,直觉模糊集和区间直觉模糊集理论被频繁地应用于决策领域[3-4]。基于区间直觉模糊集,Atanassov等[5-6]定义了其基本运算法则;Xu等[7-8]定义了区间直觉模糊集几何算子,如:加权几何集成算子(IIFWGA)、加权算术集成算子(IIFWAA),同时提出了一种基于精确函数和得分函数的多准则决策过程的直觉模糊集排序方法。此后,随着精度函数理论与多准则决策理论相结合,研究逐步深入,区间直觉模糊集的排序对于处理不完整和模糊信息发挥了越来越重要的作用。2007年,Xu[7]提出了通过比较区间直觉模糊集的得分函数和精确函数值大小,进而对区间直觉模糊集进行排序的方法。但Xu的方法未全面考虑区间直觉模糊集涉及的信息,所以存在较多排序失效或与实际情况不符的情形。因此,很多学者先后提出了一些不同的得分或者精确函数[9-14],但都存在排序失效的情况以及不合理之处。

本文首先介绍IFS和IVIFS基础知识;然后引入区间直觉模糊加权算术平均算子以及加权几何平均算子;接着介绍现有的得分函数以及精确函数,并且分析其中的不合理性,提出新的精确函数;最后用实例说明新提出的精确函数的有效性、可行性。

1 区间直觉模糊集的基本知识

设X是一个给定的非空论域,其上的一个区间直觉模糊集A被定义为以下形式:

A={x,uA(x),vA(x)|x∈X}

(1)

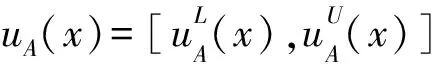
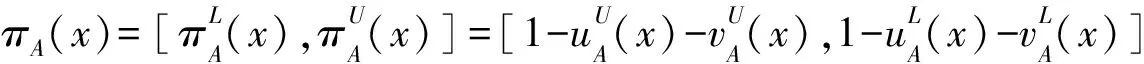
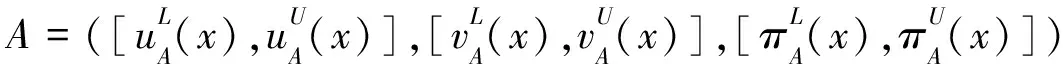
(2)

Ac={x,vA(x),uA(x)|x∈X}

(3)

为简化形式,记α=([a,b],[c,d])为一个区间直觉模糊集,其中0≤a≤b≤1, 0≤c≤d≤1, 0≤b+d≤1。区间直觉模糊加权算术平均算子[7]为

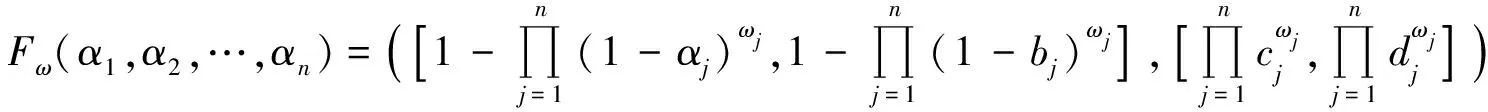
(4)

区间直觉模糊加权几何平均算子为

(5)

公式(4)侧重于群体影响,对个体对象的影响不敏感,相反,公式 (5)侧重于个体影响。

众多区间直觉模糊集学者先后提出了多种排序算法。2007年,Xu[7]依据得分函数以及精确函数给出了区间直觉模糊集的排序方法S(A) 和H(A),其A的得分函数S和精确函数H定义如下:

其中:S(A)∈[-1,1];H(A)∈[0,1]。通过得分函数进行排序,在得分函数相同的情况下,比较精确函数的大小进行最终的排序,但是这个方法未考虑到隶属度区间和非隶属度区间大小。

2008年,Ye[9]提出了精确函数M(A):

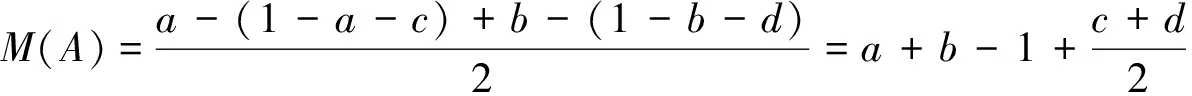
(8)

其中M(A)∈[-1,1]。Ye将区间直觉模糊值的犹豫度引入了精确函数,然而公式(8)中在精确函数隶属度、非隶属度大小不变的情况下,精确函数M与非隶属度区间的长度无关。

2010年,Nayagam等[10]介绍了新的精确函数L(A):

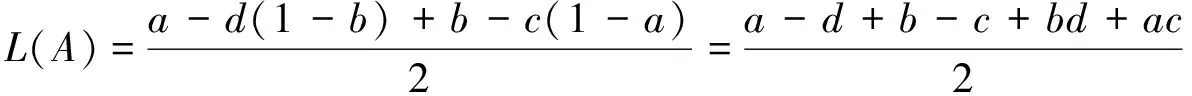
(9)

2016年,Sahin[11]定义了精确函数K(A):

(10)

2017年,Zhang等[12]定义了精确函数F(A):

2019年,Priyadharsini等[13]定义一个精确函数P(A):

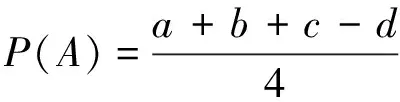
(12)

2 精确函数N(A)

结合Xu提出的得分函数S(A)和精确函数H(A),同时考虑到各方面信息对决策的影响以及隶属度和非隶属度的对比程度,本文提出一个新的精确函数N(A):

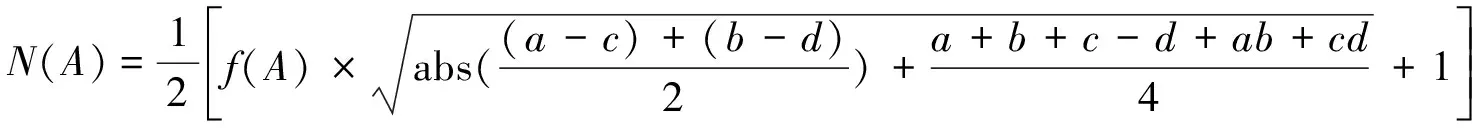
(13)

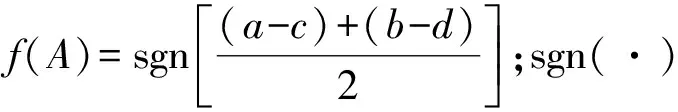
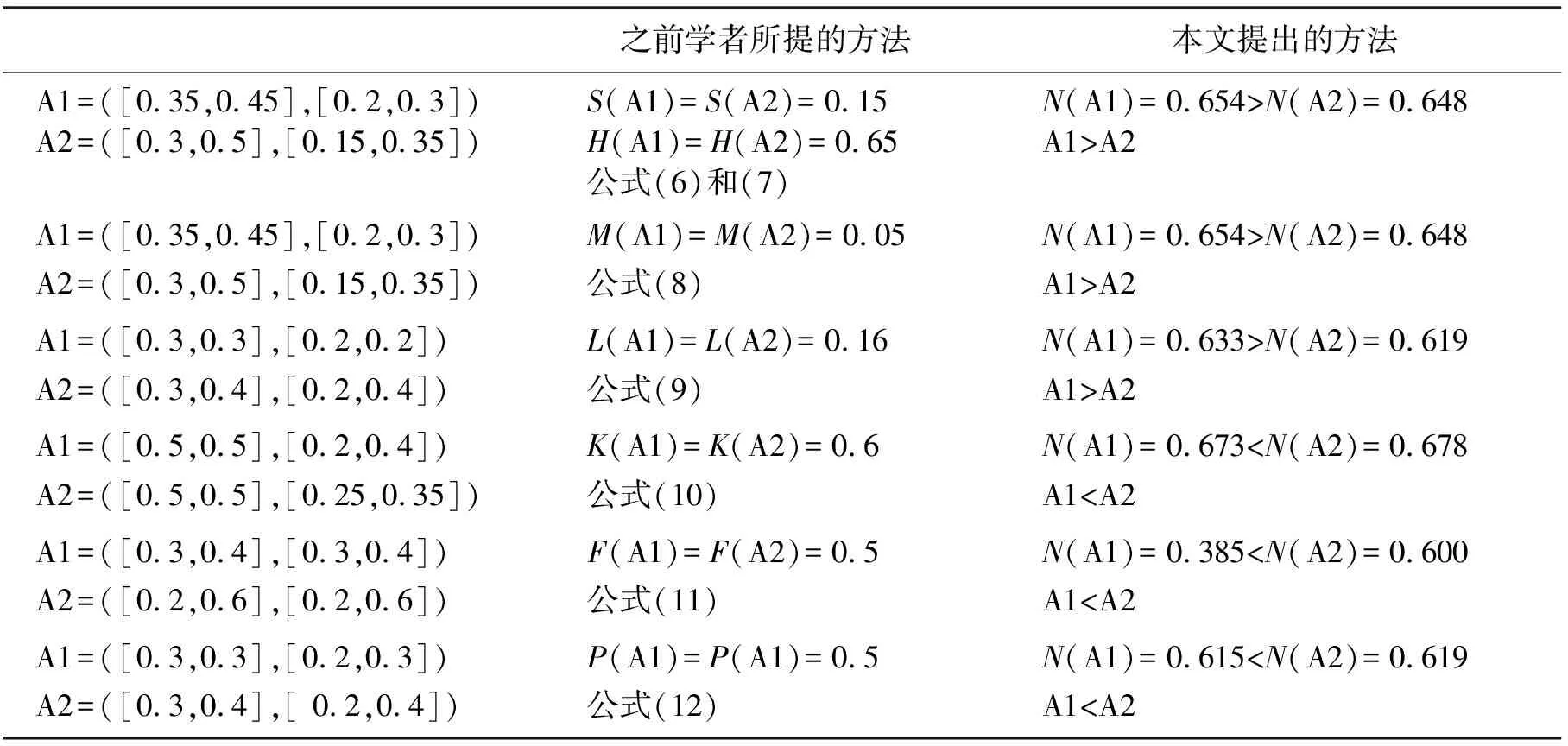
表1 各个排序方法的值Table 1 The values of each ranking method

3 决策步骤

综上,本文提出一种基于改进的区间直觉模糊集排序方法的多准则决策算法,具体步如下:

步骤1 对于某多准则决策问题,设C为准则集,C={Cj|j=1,2,…,n},决策者给出候选方案集A,A={Aj|j=1,2,…,m},决策者对候选方案Ai∈A(i=1,2,…,m) 关于准则Cj∈C(j=1,2,…,n) 进行测度,得到属性值为区间直觉模糊集rij=([aij,bij],[cij,dij])。其中,[aij,bij]表示决策者对于方案Ai关于准则Cj的支持程度的上界和下界,[cij,dij]表示决策者对于方案Ai关于准则Cj的不支持程度的上界和下界。将决策者给出的所有候选方案在各准则上的区间直觉模糊集组成一个决策矩阵为

R=(rij)m×n,i=1,2,…,m,j=1,2,…,n

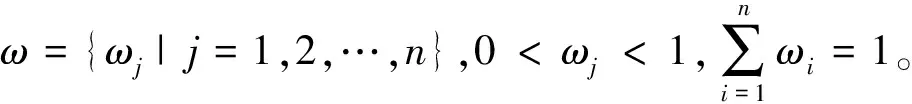
步骤3 为突出所有准则对于方案的决策作用,根据步骤1得到的决策矩阵和步骤2的权重值集合的结果,利用区间直觉模糊加权算术平均算子(4),求出决策方案Ai的综合属性值ri(i=1,2,…,m),此步结合准则权重将决策矩阵转成决策向量。其中

步骤4 利用本文提出的精确函数(13),依据步骤3得到的各备选方案的综合属性值ri求出各候选方案Ai(i=1,2,…,m)的精确函数值N(ri)。

步骤5 根据精确函数值N(ri)由大到小对备选方案排序,N(ri)值最高者所对应的备选方案为综合考量后的最佳方案。

4 实例分析

某投资公司根据3个评价准则(风险分析C1,成长分析C2,环境影响分析C3),对4家可供选择的企业(汽车公司A1,食品公司A2,IT公司A3, 武器装备公司A4)进行评估。假设3个准则的权重分别为W=(0.35,0.25,0.40)。该实例被Herrera等[16]和Sahin等[11]用来证明新提出排序方法的有效性,本文所有计算函数均采用开源的统计建模语言R语言编写。

决策者给出每个备选方案的区间直觉模糊集,如表2所示。

表2 备选公司在各准则的评价信息Table 2 Evaluation information of candidate companies in each criteria

利用公式(4)计算出4个备选公司的综合属性值分别为

利用新提出的精确函数公式(13),求出4个备选方案的精确函数值分别为N(r1)=0.375 0,N(r2)=0.718 0,N(r3)=0.672 0,N(r4)=0.725 0。因此,4个备选方案的排序为A4>A2>A3>A1,最优的方案为武器装备公司A4。

表3是Ye等计算该实例的结果。只有Zhang等[12]的F(A) 排序结果与本文新提出的精确函数N(A)得出的排序一致。由表2可见,在指标C1的区间值模糊集中,A4的隶属度比A1的隶属度大0.1,同时A4的非隶属度比A2的非隶属度小0.1;反过来,在指标C3中,A2的隶属度比A4的隶属度大,然而C3指标的权重值仅仅只比C1大0.05。根据上述的分析,备选方案A4(武器公司)比A2(食品公司)的得分稍高,在综合属性值r2和r4中,r2的非隶属度大于r4,隶属度基本保持一致,所以可以得出备选方案A4优于A2。

表3 各文献中的值和排序情况Table 3 The values and ranking in the literatures

5 结 语

本文针对现有的排序函数,包括得分函数和精确函数,分析了排序失效的情况或者不足之处后,提出了一个新的精确函数,采用侧重于整体影响的区间直觉模糊加权算术平均算子对区间模糊集的相关信息进行集合,进而根据新的精确函数对备选方案进行排序。通过实例分析比较,本文所提出的精确函数能够在一定程度上克服其他排序函数存在的不足,有利于做出更好的决策。