圆锥型水轮旋转现象的数学模型及其仿真

王贺元, 梅鹏飞

(沈阳师范大学 数学与系统科学学院, 沈阳 110034)

0 引 言

混沌的历史最早追溯到Poincare对三体问题的研究[1]。1963年,气象学家Lorenz[2]在研究局部区域小气候的数值实验中发现了混沌现象,从而开启了混沌研究的先河。Lorenz方程揭示的混沌现象引起了人们极大的研究兴趣,进而引发了探索热潮[3-9]。人们在研究Lorenz系统混沌行为的同时,一直都在探索设计与Lorenz系统对应的实验装置[9-13]。本文首先构建圆锥型水轮旋转的数学模型,其次探讨数学模型的动力学行为,进而解释和分析水轮的混沌旋转现象。

1 圆锥型水轮旋转装置

圆锥型水轮旋转装置由2个同轴等高的圆锥组成,圆锥间存在小的间隙,间隙之间加薄板,将公共顶点挖去,制作漏水的小孔,漏水率为k,注水器位于装置的最高点,注水率Q大小可以人工调节,圆锥的公共轴制作成可调节摩擦的转轴,整个装置与水平面有非零夹角φ,保证注水后水轮可以旋转。

2 圆锥型水轮的数学模型

2.1 建立质量守恒方程、力矩平衡方程

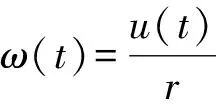
取水腔内控制体的体积为V,V内流体质量变化取决于顶部的注入、对流和底部的流出,在t时刻的变化为

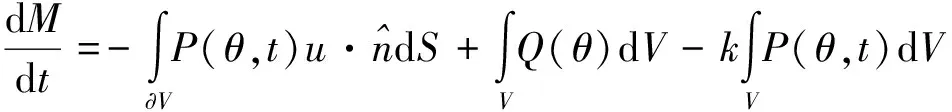
(1)

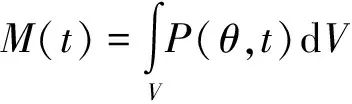
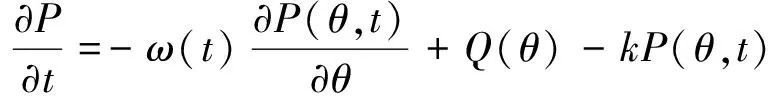
(2)

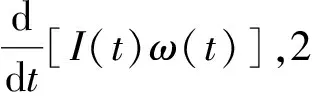
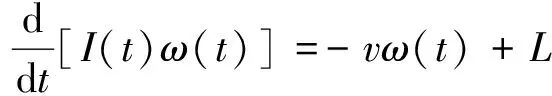
(3)

下面对转动惯量I(t)和重力矩L进行详细推导和计算。以旋转轴为轴建立如图 1所示坐标系。

图1 坐标系Fig.1 Coordinate syste

由于水腔微元水的质量分布密度为P(θ,t),设整个水轮间隙区域为Ω,取如图2中薄圆台型的一小段为水微元dv,则水腔内水微元质量为P(θ,t)dv,水轮中水的高度为z,变化范围为[0,h],在水微元形成的圆环形液面中小圆半径为r0,大圆半径为R0,水轮中水的转动惯量为

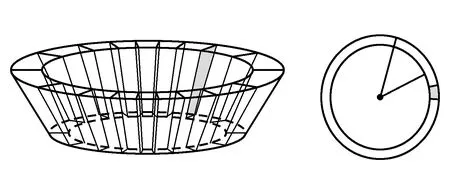
图2 水微元示意图Fig.2 Water micro element diagram

令A=(cot4β-cot4α)h5,则

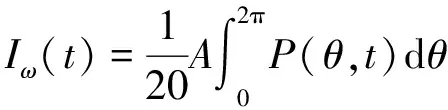
(4)

小微元体所受到的重力为P(θ,t)dv·g,这里g为重力加速度垂直于旋转轴的分量。根据力矩公式,可得微元的重力矩为P(θ,t)dv·g·rsinθ。水轮装置间隙区域Ω内水的重力矩为

令B=(cot3β-cot3α)h4,则重力矩:

因而力矩平衡方程(3)化为如下方程:

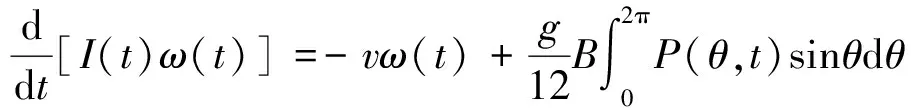
(5)

方程(2)和方程(5)即为圆锥型水轮旋转现象的数学模型。

2.2 数学模型的简化

由于圆锥型水轮的数学模型(2)和模型(5)是连续的,下面通过傅里叶展开简化模型(2)和模型(5),以便进行理论分析和数值仿真。对水质量分布密度P(θ,t)展开成傅里叶级数:

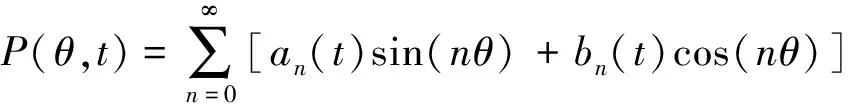
(6)

由于圆锥型水轮旋转时的水是对称注入的,因此对其中的注水率Q(θ)进行傅里叶展开有

将此式和式(6)代入方程(2)和方程(5)整理,利用待定系数法得

圆锥型水轮旋转轴水平时的方程与方程(7)取n=1时导出的结果相似,但在这种情况下,推导出的是对应粗糙近似真实的系统[14],所以对倾斜情况讨论时,只能通过一个无穷小的连续系统做出近似,代替有限大小的隔间。最初,水轮是空的,对应所有的n,都有an=bn=0。

由圆锥型旋转水轮中水的转动惯量为

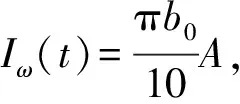
从而得

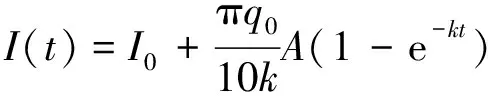
(8)

因此,总转动惯量I(t)随时间而变化,与水轮的转动速度没有关系,根据式(8)可知:当n=1时,方程组(7c)与其他方程模态解耦;当n≥2时其为高模态,只影响装置注水的细节,不影响水轮转动。从而可得动力系统是由如下3个方程耦合而成:

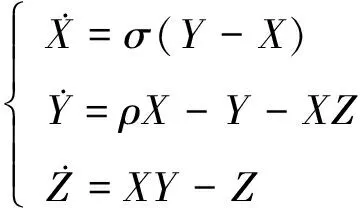
(9)

式(9)为圆锥型水轮旋转问题简化的数学模型。

3 数学模型动力学行为的仿真研究

取σ=4,模型系统的动力学行为随着ρ的大小变化而变化。图3为当0<ρ<300时的分叉图,图4为对应的最大Lyapunov指数图。当ρ=1.065 386,模型开始出现分叉;当ρ>16时,混沌开始出现,混沌区中在75.688<ρ<110时出现一个明显的周期窗口。

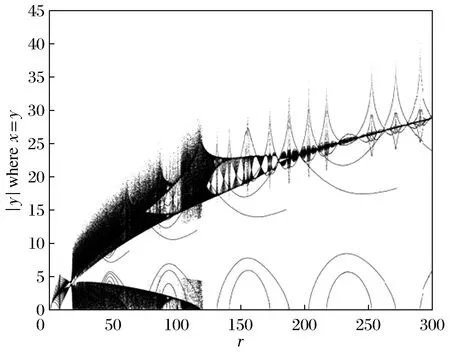
图3 σ=4时状态变量y的分叉图Fig.3 Bifurcation graph of state variable y when σ=4

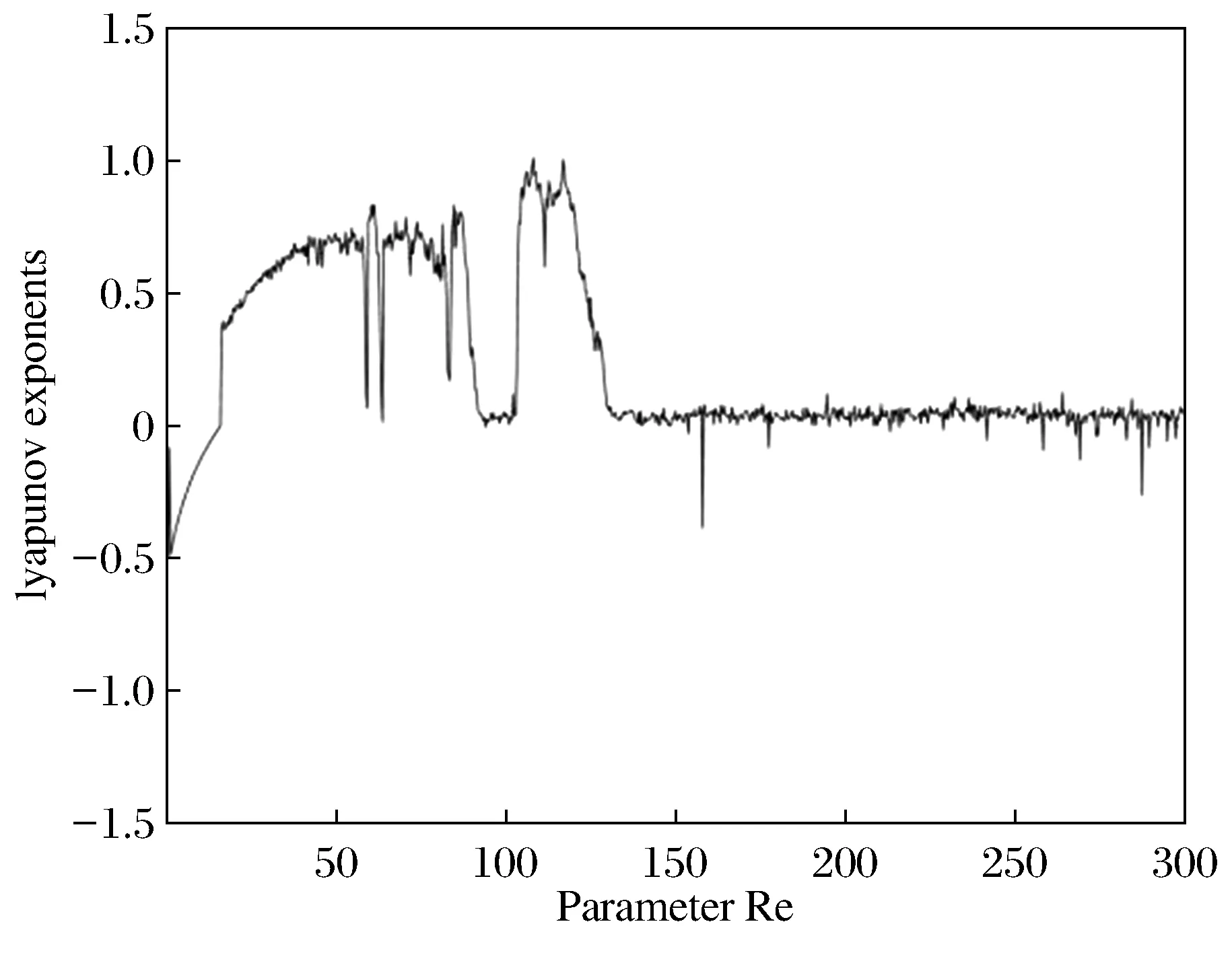
图4 σ=4时的最大Lyapunov指数Fig.4 The largest Lyapunov exponent when σ=4

从上述指标图的特征可以看出模型(9)在ρ>16时展现混沌状态。

4 结 语

本文利用微元法结合力学原理,通过傅里叶变换,推导出圆锥型水轮旋转现象对应的数学模型为三维非线性微分方程组。运用MATLAB软件绘制混沌指标图,展示了数学模型的混沌行为,进而对水轮混沌旋转现象给出了合理性的解释。