相容半连续格的序同态

陈必琴，姜广浩

（淮北师范大学数学科学学院，安徽淮北 235000）

0 引言

为研究计算机程序设计语言相关问题，Scott 在文献[1]中引入了连续格的概念.后来，赵东升基于文献[2]在[3]中提出了半连续格的概念.文献[4]为国内学者最早研究半连续格理论的文献，并引起了国内学者对半连续格的广泛关注.文献[5]借助于半素极小集给出了半连续格序同态扩张定理.文献[6]引入并研究了相容半连续格.受上述研究的启发,本文将引入相容半连续格的概念，并研究其性质，探讨其序同态.

1 预备知识

定义1.1[2]设I是格L的理想,∀x，y，z∈L,若x∧y∈I,x∧z∈I时,有x∧(y∨z) ∈I,则称I为L的半素理想，记Rd(L)={I：I是半素理想}.

定义1.2[6]设L是格,x，y∈L,若∀S∈Rd(L),supS存在,且y≤supS,有x∈S,则称x弱⇐y,记为x⇐wy（∀x∈L,令⇓wx={y∈L：y⇐wx}）.

定义1.3[6]设L是格,S∈Rd(L),若∃x∈L,使S⊆⇓wx，则称S为相容半素集，记Ic(L)={S：S是L的相容半素集}.

定义1.4[6]任一相容半素集都有并和交的格称为相容完备格.

定义1.5[6]在相容完备格L中,若x，y∈L,∀S∈Ic(L)，y≤supS,有x∈S，则称x相容⇐y,记为x⇐cy（令⇓cy={x∈L：x⇐cy}）.

定义1.6[6]若∀x∈L,有x≤sup ⇓cx,则称相容完备格L是相容半连续的.

定义1.7[6]设x∈L,B∈Ic(L),若B≠∅且满足：

（1）x≤supB；

（2）∀S∈Ic(L),若x≤supS,则∀b∈B,∃s∈S,使得b≤s,则B称为x处的相容半素极小集.

2 主要结论

（2）映射f：L1→L2称为保相容半素并,若f保序且∀S∈Ic(L1),f(supS)=supf(S).

定义2.2设L1,L2是相容完备格,映射f：L1→L2称为序同态,如果f，f-1保相容半素并，其中f -1:L2→L1是f的逆映射,定义f-1(b)=sup{↓a∈L1：f(↓a)⊆↓b}.

定义2.3设L1,L2是相容完备格,映射f：L1→L2称为保⇐c的,若a⇐cb可推出f(a) ⇐c f(b).

定理2.1设f：L1→L2,L1是相容半连续格,则f是序同态当且仅当f保相容半素并和⇐c.

证明设f是保相容半素并的和保⇐c的,只需证f-1保相容半素并.设S∈Ic(L)且s=supS,由于f-1是保序的,因此只需证f-1(s) ≤supf-1(S),任取u⇐c f-1(s),由f保⇐c,有f(u) ⇐c ff-1(s) ≤s=supS,则∃x∈S,使得f(u) ≤x,故有u≤f-1(x) ≤supf-1(S).又因为L1是相容半连续格,有f-1(s)=sup{u∈L2|u⇐c f-1(s)}≤supf-1(S),故f-1(supS)=supf-1(S),即f是序同态.

设f是序同态,只需证f是保⇐c的.设a⇐cb,又设S∈Ic(L) 且满足f(b) ≤supS,令s=supS,则b≤f-1(s)=f-1(supS).由于f-1保相容半素并,故有b≤sup(f-1(S)).又由f-1保序知f-1(S)是L1中的相容半素集,故 由a⇐cb知,∃x∈S,使 得a≤f-1(x),即f(a) ≤x.故f(a) ⇐c f(b).

定义2.4设L1,L2是相容半连续格,映射f：L1→L2称为保相容半素极小集,若∀a∈L1,当B是a的相容半素极小集时,f(B)是f(a)的相容半素极小集.

定理2.2设映射f：L1→L2保序,L1,L2为相容半连续格,则有等价条件:

（1）f保相容半素极小集；

（2）∀a∈L1,↓f(⇓ca)是f(a)的相容半素极小集；

（3）f保相容半素并,且∀a∈L1,有f(⇓ca)⊆⇓c f(a)；

（4）f是序同态.

证明（1）⇒（2）由L1是相容半连续格,∀a∈L1,⇓ca是a处最大的相容半素极小集.故由(1)有↓f(⇓ca)是f(a)的相容半素极小集.

（2）⇒（3）由条件知∀a∈L1,有f(⇓ca) ⊆⇓c f(a),故f保⇐c.又L2为 相容 半连 续格,故有f(a)=sup ⇓c f(a)=supf(⇓ca).设S∈Ic(L1),记a=supS,则由命题2.1 可知

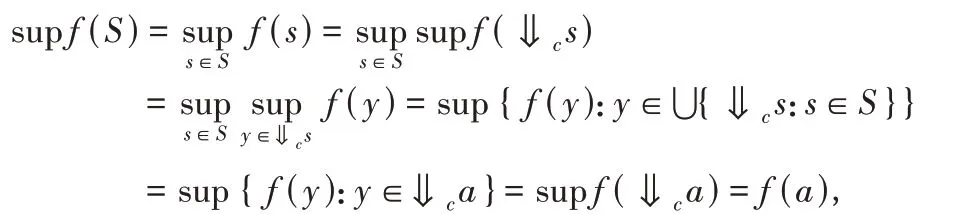
故f保相容半素并.

（3）⇒（4）显然.

（4）⇒（1）设a∈L1且B是a的相容半素极小集,由文献[6],有a≤supB且B⊆⇓ca.由f保⇐c，有f(B) ⊆f(⇓ca) ⊆⇓c f(a).又 由f保相容半素集,有↓f(B)∈Ic(L2);再 由f保相容半素并,有supf(B)=f(supB) ≥f(a).

推论2.1设L1,L2是相容半连续格,映射f：L1→L2保序,则f为序同态当且仅当f保相容半素极小集.

定理2.3设L1,L2是相容半连续格,映射f：L1→L2保⇐c,a∈L1,令f*(a)=supf(⇓ca),则f*是最大的,取值小于或等于f的保相容半素并和⇐c的映射.

证明（1）f*的定义是合理的.

（2）f*保相容半素并.∀X∈Ic(L1),由条件知f*保序,且f*(X) ∈Ic(L2).令z=supX,则

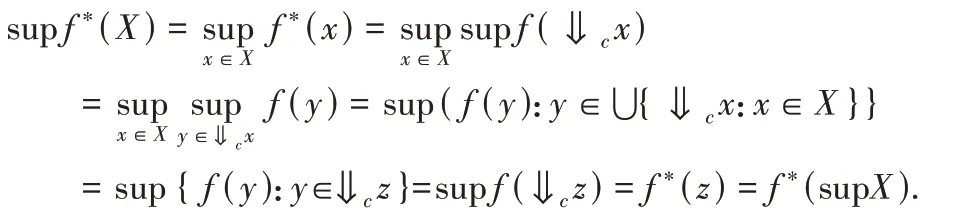
（3）f*保⇐c.∀a，b∈L1,a⇐cb,则∃m∈L1,使得a⇐cm⇐cb.由f*的定义知f*(m) ≤f*(b).设x∈⇓ca,由f保⇐c知f(x) ⇐c f(a) ⇐c f(m),故f(x) ≤f(a) ≤f(m),从而有f*(a)=supf(⇓ca) ≤f(a) ⇐c f(m) ≤f*(b).

（4）f*的最大性.由f*的定义可知f*≤f.若∃g≤f且g保相容半素并和 ⇐c,则 ∀a∈L1,g(a)=f(sup ⇓ca)=supg(⇓ca) ≤supf(⇓ca)=f*(a),即g≤f*.