基于围长约束与EMD的低错误平层LDPC码构造方法
袁建国,王宏森,张希瑞,范福卓,袁 梦
(重庆邮电大学 光通信与网络重点实验室,重庆 400065)
0 引 言
随着通信技术的日益发展,人们对通信可靠性的要求越来越高,而在实际的通信系统中,一定会存在干扰,所以需要使用信道编码技术提升通信系统的可靠性。1962年,Gallager发现了低密度奇偶校验(low-density parity-check, LDPC)码。LDPC码是一种能发现并纠正误码的信道编码技术,并且其纠错性能接近香农限[1-3],因而受到广大研究者的关注,并且应用于无线通信,深空通信,数字水印技术,快速数据存储系统,超高速光纤传输等方面[4],其实际意义和经济价值很大。目前,LDPC码也已经成为了5G编码方案的标准码之一。
LDPC码的错误平层问题是指在一定的高信噪比区域,误码率性能曲线的斜率突然减小甚至接近于0的现象。近年来,为了使LDPC码具有更好的纠错性能,许多研究者提出了一系列降低错误平层的方法。文献[5]提出了一种采用算术约束和小陷阱集约束的斜率序列来构造(3,k)LDPC码的方法,该方法构造出的LDPC码中不存在(5,3),(7,3),(6,2)和(8,2)陷阱集,降低了错误平层。文献[6]提出了在Tanner图中利用图覆盖消除校验矩阵中的陷阱集的方法。文献[7]提出了一种利用数列分割移位的方法来减少Tanner图中陷阱集的个数,从而达到降低错误平层的效果。文献[8]提出以平均围长为约束条件,逐列构造校验矩阵,以局部优化平均围长为目的构造LDPC码,使得LDPC码具有更低的错误平层,但是这种方法构造出的LDPC码中会存在一些连通性差的环,这同样也会影响码字的纠错性能。
针对LDPC码中的错误平层问题,本文将围长约束与额外信息度(extrinsic message degree, EMD)算法结合起来,提出了一种基于围长约束和EMD的低错误平层LDPC码构造方法。在该方法中,首先将围长约束与渐进边增长(progressive edge growth, PEG)算法进行结合,然后提升构成环的变量节点的EMD值,最后通过添加一个校验节点对校验矩阵中的环的连通性进一步提升,得到最终的校验矩阵H。仿真结果表明,利用本文提出的方法构造的LDPC码型,有效改善了在高信噪比区域的错误平层现象。
1 PEG算法简介
PEG算法是一种经典的随机构造方法[9]。该算法是在满足所需度分布的情况下,通过逐个添加校验矩阵中变量节点和校验节点之间的边,使得变量节点的局部围长最大,由此来构造出奇偶校验矩阵对应的Tanner图。在构造校验矩阵的过程中,设置合适的校验矩阵大小,以便灵活调整LDPC码的码长码率,再根据密度进化算法来选取合适的度分布,从而使构造出的LDPC码具有良好的纠错性能。其中,校验矩阵中各个节点的度分布定义为
(1)
(1)式中:dv表示所有校验节点与某一变量节点连接边数的最大值,即最大列重;dc表示所有变量节点与某一校验节点连接边数的最大值,即最大行重;λi表示校验节点与所有度为i的变量节点之间连接边数占Tanner图中总边数的百分比;ρi表示变量节点与所有度为i的校验节点之间连接边数占总边数的百分比。虽然PEG构造在添加新的边时能够保证当前边所在环的环长尽可能大,但是这仅仅是从局部进行考虑的,并不能从全局角度去优化校验矩阵中存在的环,这会导致校验矩阵中环结构比较复杂,特别是在码长较长情况下,各个环之间会存在大量的公共节点[10],又因为环是在译码过程中重要的信息传递路径,所以会在一定程度上降低迭代译码的性能。
2 基于围长约束与EMD的低错误平层LDPC码构造
2.1 LDPC码中围长的约束
本文将Tanner图中变量节点记为VN,校验节点记为CN。从任意VN出发,依次经过CN和VN,最后回到出发节点的路径称为环。记经过不同变量节点数量为d,则环长为l=2d。Tanner图中最短的环长叫作围长。通过一个变量节点的最短环长度称为变量节点的局部围长,校验矩阵的平均围长(girth average, GA)定义为[11]
(2)
(2)式中:k为第i个变量节点的局部围长的一半;lmax为所有变量节点的最大围长;gi(l)为局部围长为l的变量节点占总变量节点的百分比。
以PEG算法为框架,逐列进行校验矩阵的构造:首先,根据密度进化理论选取合适的变量节点度分布;然后,计算出各个度对应的变量节点个数,并根据各变量节点的度大小依次排列;最后,在构造各列矢量时,按照各个约束条件进行构造。在文献[8]中,其构造规则归纳如下。
步骤1设置校验矩阵的大小为(m,n),变量节点序号为i,且i=1,2,…,n,初始化i=n。
步骤2记循环生成第i个变量节点的次数为N,初始化N=0。
步骤3在符合设定度分布的条件下,随机生成第i个变量节点对应的列向量。
步骤4若i-n+1≤m,判断新生成的列向量是否与之前生成的列向量线性无关,若线性无关,执行步骤5,否则执行步骤3。
步骤5令N=N+1,利用(2)式计算当前节点的平均围长,并与之前记录的最大平均围长进行比较,并记录下较大值。
步骤6若N=C,令i=i-1,执行步骤7,否则执行步骤3。
步骤7若i=0,算法结束,否则执行步骤2。
该算法对于每个变量节点都构造了C个列矢量,对C的选取是一个比较困难的问题,若C过大,则算法复杂度会较高;若C过小,则构造出的LDPC码的局部围长也会较小。并且以这种方法构造出的LDPC码会存在环的连通性较差的情况。因而本文将对此算法予以改进。
2.2 提升校验矩阵中环的连通性
在LDPC码的迭代译码过程中,环作为消息传递的路径,对码字的纠错性能起着至关重要的作用。连通性差的环对LDPC码的迭代译码性能影响非常大,因而本文从增大环的连通性角度,提出一种降低LDPC码错误平层的改进构造方法。
环的连通性通常可用EMD或者近似环额外信息度(approximate extrinsic message degree, ACE)[12]来表示。对于额外信息度,有如下定理。
定理1对于变量节点集合L,如果存在仅与集合L只连接一次的校验节点,那么该校验节点称为集合L的外节点。集合L的外节点个数称为变量节点集合L的EMD值[13]。
ACE值是针对构成环的变量节点集合EMD值的近似计算,且ACE值是EMD值的上限值。所以用ACE值对环的连通性度量并不如使用EMD值更加精确,虽然EMD值计算会比ACE值计算复杂,但是在本方法中,仅需计算构成环的变量节点EMD值,并且可利用基于树图的环统计方法进行环统计,因此,二者的运算复杂度比较接近。对此采用EMD值来度量环的连通性。
构造(m,n)校验矩阵的算法流程图如图1。

图1 校验矩阵构造流程图Fig.1 Check matrix construction flow chart
首先,使用改进的算法构造(m-1,n)的矩阵H1,对H1中环的连通性进行局部优化。改进算法流程归纳如下。
步骤1设置矩阵大小为(m-1,n),设置平均围长阈值γav,EMD阈值η,变量节点序号为i,且i=1,2,…,n,初始化i=n。
步骤2在符合设定度分布的条件下,随机生成第i个变量节点对应的列向量。
步骤3若i-n+1≤m,判断新生成的列向量是否与之前生成的列向量线性无关,若线性无关,执行步骤4,否则执行步骤2。
步骤4利用(2)式计算当前节点的平均围长gav,并计算构成最小环的变量节点EMD之和,记录其和的值为ηi。
步骤5若gav≥γav且ηi≥η,令i=i-1,执行步骤6,否则执行步骤2。
步骤6若i=0,算法结束,否则执行步骤2。
此时,完成了对校验矩阵的围长约束和环的连通性初步优化。
然后,利用基于树图的环搜索方法遍历搜索H1中的所有不大于lth的环,并计算其中包含的变量节点EMD值和对应变量节点序号,并记录到列表φ中,再筛选出φ中的最小EMD值,并按照出现次数从多到少对变量节点进行排序,分别记为vmi,i=1,2,…。通过添加一个校验节点cm,将cm与vmi相连,判断是否存在长度小于γav的环,若存在,则删去连接的边,选择下一个变量节点相连,直到cm的度接近校验节点的平均度分布,得到一个n维行向量hm,此时进一步提升了构成环的数量较多的变量节点连通性。
(3)
最后,将H1和hm如(3)式所示进行合并,得到最终的校验矩阵H。
由于本文所构造的LDPC码码率为k=1-n/m,所以只要选取合适的码长n和校验节点数目m,就可灵活调整码长码率,得到能适用于不同系统且满足需要的LDPC码。
3 性能分析
3.1 仿真分析
根据本文所提出的一种基于围长约束和EMD的低错误平层LDPC码构造方法,分别构造了码长为3 024,码率为0.5和码长为1 200,码率为0.67的LDPC码,并进行了Matlab仿真分析,以此验证本文构造方法的性能。本文仿真条件:二进制相移键控(binary phase shift keying,BPSK)调制,加性高斯白噪声(additive white gaussian noise,AWGN)信道,置信传播(belief propagation,BP)译码,综合折中考虑纠错性能与译码复杂度,译码迭代次数选择50次。

图2 PGAE-LDPC(3 024,1 512)码与其他码的纠错性能仿真图Fig.2 Simulation diagram of the error-correctionperformance among the PGAE-LDPC(3 024,1 512) code and other codes
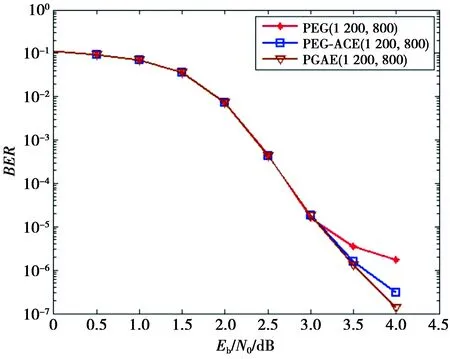
图3 PGAE-LDPC(1 200,800)码与其他码的纠错性能仿真图Fig.3 Simulation diagram of the error-correctionperformance among the PGAE-LDPC(1 200,800) code and other codes
本文根据密度进化算法,设定校验矩阵的度分布为λ(x)=0.383 54x+0.042 37x2+0.574 09x3,校验矩阵大小分别为m=1 512,n=3 024和m=400,n=1 024构造得到的PEG-GA-EMD(PGAE)-LDPC(3 024,1 512)码型和PGAE-LDPC(1 200,800)码型,与利用PEG算法得到的PEG-LDPC码型、利用PEG算法和围长约束得到的PEG-GA-LDPC码型以及利用PEG算法和ACE算法[14]得到的PEG-ACE-LDPC码型进行仿真对比分析。其误码率性能仿真对比图分别如图2和图3。
本文构造的码率为0.5的PGAE-LDPC(3 024,1 512)码和码率为0.67的PGAE-LDPC(1 200,800)码的围长均为8,由图2和图3分析可知,PGAE-LDPC(3 024,1 512)码在误码率为10-6时,相较于PEG-ACE-LDPC(3 024,1 512)码,净编码增益提升了大约0.04 dB,相较于PEG-LDPC(3 024,1 512)码,净编码增益提升了大约0.22 dB,相较于PEG-GA-LDPC(3 024,1 512)码,净编码增益提升了大约0.20 dB,在误码率为10-7时,本文构造的码率为0.5的PGAE-LDPC(3 024,1 512)码,相较于PEG-ACE-LDPC(3 024,1 512)码,净编码增益提升了大约0.25 dB;且在信噪比为2.2 dB时,PGAE-LDPC(3 024,1 512)码的误码率为4.64×10-8,PEG-ACE-LDPC(3 024,1 512)码的误码率为3.31×10-7,PEG-GA-LDPC(3 024,1 512)码的误码率为5.47×10-7,PEG-LDPC(3 024,1 512)码的误码率为7.30×10-7。本文构造的码率为0.67的PGAE-LDPC(1 200,800)码在误码率为10-6时,相较于PEG-ACE-LDPC(1 200,800)码,净编码增益提升了大约0.09 dB,相较于PEG-LDPC(1 200,800)码,净编码增益提升了大约0.77 dB。尤其是基于本文方法所构造的PGAE-LDPC(3 024,1 512)码和PGAE-LDPC(1 200,800)码不存在明显的错误平层现象,而其他几种LDPC码型存在明显的错误平层现象。
3.2 复杂度分析
从编码复杂度的角度来看,基于本文构造方法所构造的LDPC码相较于文献[8]基于围长约束构造的PEG-GA-LDPC码、文献[14]利用经典PEG方法构造的PEG-LDPC码和基于PEG与ACE构造的PEG-ACE码,具有相同的码长码率,且都是通过生成矩阵进行编码,四者的编码运算复杂度均是O(n2)。唯一不同的是,本文在构造校验矩阵的过程中,有一个额外的遍历搜索矩阵中连通性较差的变量节点的过程,这个过程在构造LDPC码的过程中只存在一次。在本文构造的码长为3 024的PGAE-LDPC(3 024,1 512)码和码长为1 200的PGAE-LDPC(1 200,800)码时,此过程的耗时分别仅为63.47 s和54.18 s,运算复杂度会有略微增加。综上分析可知,本文提出的构造方法与文献[8]和文献[14]相比,在仅增加可接受的运算复杂度情况下,纠错性能得到明显改善的同时,也进一步降低了其错误平层。
4 结 论
为了消除或降低高信噪比区域LDPC码存在的错误平层现象,本文提出了一种基于围长约束和EMD的低错误平层LDPC码构造方法,首先约束校验矩阵的围长,并初步提升构成环的变量节点EMD值,然后通过添加一个校验节点,再次提升构成环数量较多的变量节点的连通性,从而得到最终的校验矩阵。仿真结果表明,利用本文提出的构造方法所构造出的LDPC码型中不存在四环和六环,码字的纠错性能优于基于PEG算法与ACE相结合构造的同码长码率的码型,同样也优于PEG算法结合围长约束构造的同码长码率的码型。本文提出的方法,一方面保证了LDPC码围长足够大,另一方面提升了环的连通性,从而减小了小陷阱集出现的概率,特别是在高信噪比区域,有效地改善了LDPC码的纠错性能,并且具有较低的错误平层。

