基于改进LSSVR模型的移动节点定位技术研究

郭 悦，王红军

(国防科技大学 电子对抗学院，合肥 230037)

0 引 言

随着物联网的不断发展，人们日常生活中出现了越来越多基于物联网技术构建的应用。其中，精确的节点定位在物联网范围内具有广阔的应用前景，对人们生活质量的提高和基于位置服务具有重要的保障和支撑作用。概括地讲，物联网中的节点定位[1]，即通过参考节点的信息来定位未知节点，是解决特定环境中实体定位问题(如环境监测和入侵定位)的关键技术。参考节点即测量节点，可以通过配备的全球定位系统(global positioning system，GPS)系统获得测量节点准确的位置信息；未知节点即需要确定位置的目标节点。

物联网中的定位算法根据是否需要对节点间的距离进行测量，可分为基于测距和非测距的算法。测距算法通常需要硬件设备测得节点间的距离信息，利用该距离对未知节点进行定位。常用的测距方法包括基于信号到达时间差(time difference of arrival, TDOA)、基于接收信号强度指示(received signal strength indication, RSSI)、基于信号到达时间(time of arrival, TOA)以及基于信号到达角(angle of arrival, AOA)等。其中，基于RSSI的测距方法[2-3]由于较低的操作复杂度以及较低的成本而得到广泛使用。非测距定位算法主要依据网络中节点之间的连通性实现定位，包括近似三角形内点测试(aroximate point-in-triangulation test，APIT)算法[4]、质心算法[5]以及凸规划算法[6]等。

上述算法对于物联网中静态节点的定位已取得良好的效果，但是在物联网的实际应用中常常用到移动节点的位置信息，例如智慧物流、共享单车等方面，而现有的静态节点定位技术由于不能满足定位的实时性要求而不再适用。因此，关于移动节点定位方面的研究[7-8]逐渐发展为物联网领域的热点。近年来，大数据应用的需求，有力推动了最小二乘支持向量回归模型[9-10]的不断发展。最小二乘支持向量回归(least squares support vector regression, LSSVR)是一种基于结构风险最小化的有效机器学习技术，建立在统计学基础上，即使在样本较少的情况下也表现出良好的拟合性能，在性能预测、数据监测、辨识问题等方面都得到了广泛应用，尤其在物联网中，移动节点的定位方面更是取得了长足的发展。文献[11]中提出一种基于LSSVR回归建模实现未知节点定位的方法，综合考虑了移动节点定位的准确度与实时性，展现出良好的定位性能。文献[12]中提出一种基于接收信号强度指示(received signal strength indication，RSSI)高斯滤波的LSSVR物联网节点定位方法，通过高斯函数滤除掉具有较大误差的测距值，将相对精确的测距向量输入到回归模型中，估计出节点位置信息。该算法有效降低了节点的定位误差，但是由于RSSI测量值的高斯滤波过程，使得算法定位的实时性有所降低。

研究发现，在利用LSSVR模型对移动节点定位的过程中，回归模型的正规化参数以及核函数参数的选取会对定位性能带来很大的影响。基于以上所述，文献[13]中利用具有自组织、自适应以及自学习性特征的遗传算法(genetic algorithm, GA)对LSSVR模型的核函数参数和正规化参数进行优化，然而遗传算法编码工作相对复杂且搜索速度较慢；文献[14]在传统的LSSVR定位模型的基础上，根据部分采样点预测位置与实际位置的均方误差，构造适应度函数，利用粒子群算法(particle swarm optimization, PSO)[15-16]优化LSSVR的模型参数。虽然该方法展现出了较好的优化效果，但是由于粒子群算法的基本参数是固定的，因此，存在易陷入局部寻优的缺陷，导致难以获得全局最优解位置，进而对回归模型的定位性能产生影响。针对LSSVR定位模型参数优化方面的问题，在文献[14]中PSO-LSSVR定位算法的基础上，提出一种改进粒子群算法优化LSSVR(IPSO-LSSVR)模型的移动节点定位方法，通过自适应改变惯性权重和学习因子，来提高算法的收敛速度并避免陷入局部寻优，获得具有最优参数的定位模型，提高算法的定位性能。

1 LSSVR定位模型

最小二乘支持向量回归是基于结构风险最小化原理发展而来的一种有效的机器学习技术，通过拟合特征向量与输出值的非线性关系，得到表征输入向量与输出值关系的回归模型。在物联网移动节点的定位过程中，利用已知信息构建训练样本集，拟合距离向量与节点横纵坐标的非线性映射关系，构建LSSVR回归模型。然后，将移动过程中未知节点到各个测量节点的距离向量输入到回归模型，借助LSSVR模型实现移动节点的定位。因此，基于LSSVR模型的节点定位过程主要由4个主要阶段组成，包括训练样本集的获取、回归建模、未知节点的RSSI测距以及节点定位。其流程如图1，其中，(x,y)为未知节点的估计坐标。

1)训练样本集的获取。已知定位区域为二维正方形区域，使用边长为t的方格将定位区域网格化，从而获得N个网格交点的坐标Ai(xi,yi)(i=1,2,…,N)，在定位区域内部设置M个测量节点Bj(j=1,2,…,M)。根据Ai到Bj的距离dij，可以得到任意一个网格交点到各个测量节点的距离向量Ri=[di1,di2,…,diM]。通过距离向量和网格交点坐标(xi,yi)构造模型的训练样本集，表示为

(1)

2)回归建模。以求解X-LSSVR定位模型为例，利用LSSVR对样本集λx进行训练，基于最小化结构风险准则，构造并求解最优化问题，得到

(2)

(2)式中：φ(·)为非线性映射函数；μ为权重系数向量；εi(i=1,2,…,N)为回归模型的拟合误差；ε=[ε1,ε2,…,εN]为εi组成的误差向量；b为偏置值；γ(γ>0)为正规化参数。

图1 LSSVR定位算法流程图Fig.1 Flow chart of LSSVR localization algorithm

为了对上述优化问题进行求解，一般将其转化为对偶问题，构造Lagrange函数为

(3)

(3)式中，ai为拉格朗日算子，由KKT[17]条件对函数进行运算，最终得到矩阵方程的简化形式为

(4)

(4)式中：x=[x1,x2,…,xN]T；a=[a1,a2,…,aN]T，1=[1,1,…,1]T；I为单位矩阵；Ω代表N×N阶对称矩阵，其第i行j列的元素为

K(Ri,Rj)=φ(Ri)T·φ(Rj)，i,j=1,2,…,N

(5)

(5)式中，K(Ri,Rj)为核函数，由于径向基核函数[18]具有参数较少且预测性能好等优势，文中将其作为回归模型的核函数，表示为

K(Ri,Rj)=e-‖Ri-Rj‖2/2σ2

(6)

设Q=Ω+γ-1I且H=Q-1，通过对(4)式进行求解，可以得到

(7)

a=H(x-1×b)

(8)

因此，得到回归模型的拟合函数，即X-LSSVR的定位模型为

(9)

同理，Y-LSSVR的定位模型也可以通过对样本集λy进行训练来获得。

3)未知节点的RSSI测距。当未知节点在定位区域内移动时，测量节点首先测得来自未知节点的信号强度；然后，根据RSSI测距技术，得到移动过程中未知节点到各个测量节点的距离，并将组成的距离向量R作为LSSVR模型的输入。

4)节点定位。当定位区域内至少存在3个测量节点不在同一直线上时，便可以运用LSSVR模型进行定位计算。将上述步骤中获得的距离向量输入到回归模型的拟合函数X-LSSVR，Y-LSSVR中，估计出未知节点的坐标(x,y)，实现定位功能。

2 粒子群算法及其改进

粒子群算法是一种全局搜索算法，通过模拟鸟群觅食行为发展而来，在搜索空间中寻找最优解实现优化。与其他优化算法相比，具有实现简单、搜索效率高且参数较少等优势。该算法被广泛地应用于参数的优化，并展现出很好的性能。

2.1 标准粒子群算法

粒子群算法采用位置与速度的数学模型，假设在d维搜索空间中，第i个粒子的位置为Xi=(xi1,xi2,…,xid)，i=1,2,…,n，n为粒子总数，对应粒子速度向量为Vi=(vi1,vi2,…,vid)。每个粒子都代表着在搜索空间中优化问题的一个潜在解，且具有一个由优化的函数决定的适应值(ffitness)。在迭代过程中，粒子通过对自己的适应度值进行计算，不断更新其位置与速度向量，获得2个“极值”：①个体极值Pibest=(pi1,pi2,…,pid)，即粒子自身找到的最优解位置；②全局极值Gbest=(g1,g2,…,gd)，即整个粒子种群获得的最优解位置。

根据这2个最优解，粒子通过(10)式和(11)式进行速度和位置的更新。

Vik+1=ω×Vik+c1r1(Pibestk-Xik)+

c2r2(Gbestk-Xik)

(10)

Xik+1=Xik+Vik+1

(11)

(10)—(11)式中：k是当前的迭代次数；Xik，Xik+1分别为当前迭代和下一迭代次数下粒子的位置向量；Vik，Vik+1分别为当前迭代和下一迭代次数下粒子的速度向量；c1，c2为学习因子，一般取c1=c2=1；r1，r2为[0,1]的随机数；ω为惯性权重。

2.2 改进的粒子群算法

从标准粒子群算法可以发现，粒子易于聚集在个体极值位置和全局极值位置附近，使得种群的多样性逐渐丧失，产生趋同效应，出现早熟收敛现象；在迭代进行的后期阶段，粒子种群的搜索将变得停滞，并且很容易陷入局部优化，这使得粒子的搜索精度降低。由于粒子个体的搜索速度主要由学习因子c1，c2以及惯性权重ω决定，所以，论文从以下2个方面对粒子群算法进行改进，避免其出现早熟收敛以及局部寻优的现象。

1)惯性权重的改进。在粒子群算法中，惯性权重控制着粒子的运动惯性，因此，可以通过对ω进行调整来改变粒子的搜索能力。通常，较大的ω值意味着粒子的全局搜索能力较强，而较小的ω值则意味着粒子的局部搜索能力较强。传统的PSO算法中，一般将ω设置为定值1。为了使算法的全局与局部搜索能力更加平衡，获得更好的搜索性能，论文采用一种惯性权重的自适应调整方法，随着粒子适应度函数值的改变，惯性权重自动调整其大小，具体表述为

(12)

(12)式中：ωmin是最小的惯性权重值；ωmax则为最大的惯性权重值；f是粒子当前的适应度取值；favg和fmin分别是整个粒子种群当前适应度的平均值与最小值。

2)学习因子的改进。c1为自我学习因子，用于调节自身经验的权值；c2为社会学习因子，用于调节种群经验的权值。在传统PSO算法中，c1，c2为定值，导致种群过早地陷入局部收敛。为了使算法的收敛性能得以提高，方便获得全局最优解，在迭代初期，设置较大的c1值以及较小的c2值，使粒子的自我学习能力较大、社会学习能力较小，利于其飞行于整个搜索空间中；迭代后期，设置较大的c2值以及较小的c1值，这样，使粒子的社会学习能力较大、自我学习能力较小，有利于粒子向全局最优解位置飞行。由于c1，c2的值通常为(0.5, 2.5)，因此，论文将c1，c2设置为单调递减和递增函数，表示为

(13)

(13)式中，k和kmax分别为当前迭代次数与最大迭代次数。

3 基于改进PSO算法的LSSVR定位模型参数优化

根据LSSVR模型对移动节点进行定位的原理可知，回归模型中的核函数参数σ以及正规化参数γ的选取，将会对定位性能产生很大的影响。其中，正规化参数γ用来平衡模型的拟合光滑性和拟合误差最小化，核函数参数σ则对训练样本分布的复杂情况进行反映。因此，参数γ和σ的合理取值，有利于更好地拟合距离向量与坐标之间的映射关系，使得定位模型更加可靠。通常情况下，利用经验判断或网格搜索等方法对参数进行选择，但是存在费时费力以及很难获得最优模型的缺陷。为了避免参数取值的盲目性，论文采用一种改进的粒子群算法对模型参数进行迭代寻优，以获得具有优良性能的定位模型。

在运用改进粒子群算法对模型参数的优化过程中，适应度函数的合理构造尤为重要。为了降低参数优化的复杂性，文中将少数网格交点作为测试点，根据测试点定位误差的均方值进行适应度函数的构造，通过迭代优化，确定最佳参数值。具体的适应度函数表示为

(14)

(14)式中：(xi,yi) (i=1,2,…,L)为测试点的实际位置；Ri为测试点处的距离向量；fx，fy为优化建模参数建立的回归模型。

利用改进的粒子群算法对模型参数优化的具体步骤如下。

步骤1初始化粒子群算法中的粒子群规模(sizePop)、最大迭代次数(kmax)，ωmin以及ωmax等相关参数。同时利用回归模型中的正规化参数γ以及核函数参数σ随机产生粒子向量(γ,σ)，并初始化粒子的速度。

步骤2基于粒子向量建立的LSSVR定位模型，对每个粒子的最优位置进行搜索。迭代初始，将粒子个体的初始位置作为其个体极值位置，并记录该位置(Pibest)；利用(14)式对各个位置的适应度函数值ffitness进行计算，并且将函数值最优的位置记录为全局最优位置(Gbest)。

步骤3利用(12)式，(13)式计算每次迭代时粒子的惯性权重ω以及学习因子c1，c2，并通过(10)式和(11)式更新粒子个体的速度与位置。

步骤4粒子的评估。计算粒子在每次迭代时的适应度值，如果优于其经历过的最优位置的适应度值，则更新个体极值位置，否则不进行更新；同理，如果种群中适应度值最优的位置好于当前的全局极值位置，则将该位置设置为新的全局最优位置，否则保留之前的最优值位置。

步骤5检查是否满足终止条件。如果满足终止条件，输出当前最优解的位置，否则回到步骤3继续执行循环，直到满足误差要求或达到最大迭代次数，并最终输出所得到的全局最优值位置。

步骤6获得最优参数后，将其代入LSSVR模型中进行定位计算。

使用改进的PSO算法优化LSSVR定位模型参数的流程如图2。

图2 LSSVR定位模型参数优化流程图Fig.2 Flow chart of parameters optimization about LSSVR localization model

4 仿真实验及结果分析

定位算法的仿真实验在Matlab R2016a平台下进行。实验设置一个100 m×100 m的矩形定位区域，未知节点的运动采用随机waypoint移动模型[19]，且以一定速度在定位区域内移动。设置该移动节点的初始坐标为(20,80)，先后分别沿Y轴负方向以及X轴正方向做直线运动，节点的运动速度在[0，Vmax]变化，最大速度Vmax=2 m/s，测距误差因子为10%，测量节点数量设为4个，分布于矩形区域顶点位置，网格边长t=25 m。因此，获得除矩形区域顶点位置的网格交点坐标。粒子群算法参数分别设置为ωmin=0.4，ωmax=0.9，kmax=100，sizePop=20。

为了更加有效地评估本文算法的定位性能，引入传统的LSSVR算法以及PSO-LSSVR算法进行了相应的对比。定位误差的计算式[20]为

(15)

(15)式中，(xreal,yreal)，(x,y)分别表示未知节点的实际坐标与估计坐标。为了降低偶然误差等因素带来的影响，取运行1 000次实验的平均定位误差作为仿真结果。下面分别从算法的定位效果对比，测距误差以及运动速度对定位误差的影响，定位算法稳定性与实时性分析这几个方面阐述IPSO-LSSVR算法的优越性。

4.1 算法的定位效果

为了比较3种算法在定位区域中对移动节点的定位效果，通过仿真实验，获得了LSSVR算法、PSO-LSSVR算法以及本文提出的IPSO-LSSVR算法的定位跟踪效果图，分别如图3—图5。通过对比发现，相比于LSSVR与PSO-LSSVR算法，本文提出的改进算法对未知节点移动过程中的估计位置更加接近于其运动轨迹中的真实位置，因此，定位精度有了明显提高，对移动节点具有更好的定位跟踪效果。

图3 LSSVR算法定位效果Fig.3 Localization effect of LSSVR algorithm

4.2 测距误差对定位误差的影响

在实际的应用环境中，由于测距过程存在噪声等干扰因素的影响，导致测距结果存在误差。因此，为了使得实验更符合实际情况，在实际距离测量中增加高斯误差，表示为

di=dij(1+randn×μ)

(16)

(16)式中：dij为节点间的真实距离值；μ为测距误差因子，与测距精度有关；randn为服从标准正态分布的随机变量。因此，论文将(16)式的计算值作为节点间的测距结果，实验中通过调整误差因子μ达到改变测距误差的目的。图6显示了随着测距误差不断增长，3种算法平均定位误差的变化曲线。从图6中可以看出，在测距误差不断增加的情况下，3种算法的平均定位误差均逐渐增加，但总体趋势比较平缓。从平均定位误差大小来分析，传统LSSVR算法的平均定位误差为7～9 m，PSO-LSSVR 算法的平均定位误差略小，为5.5～7.2 m，然而本文所提改进算法的平均定位误差最小，为4.5～6 m。因此，本文改进算法在定位精度方面具备一定的优势，其平均定位误差相对于LSSVR算法降低了约25.9%，相对于PSO-LSSVR算法降低了19.7%左右。

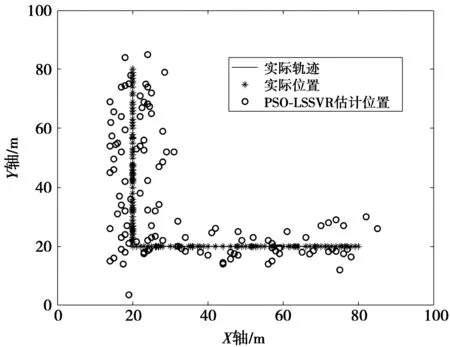
图4 PSO-LSSVR算法定位效果Fig.4 Localization effect of PSO-LSSVR algorithm

图5 IPSO-LSSVR算法定位效果Fig.5 Localization effect of IPSO-LSSVR algorithm

4.3 运动速度对定位误差的影响

由于本文是对物联网中移动节点定位方面展开研究，节点的运动速度必然会对定位误差产生一定的影响，因此，仿真时考虑了节点速度这一重要因素。定位误差随速度增长的变化曲线如图7，图7中显示了在节点的运动速度不断增加的情况下，3种算法平均定位误差的变化曲线。根据所得仿真图中的总体趋势，可以明显发现，随着节点运动速度的增大，3种算法的定位误差大体上均不断增加，即定位精度逐渐降低。与此同时，与传统的LSSVR算法以及PSO-LSSVR算法相比，本文提出的IPSO-LSSVR算法的平均定位误差总是最小，即定位精度更高。因此，当节点的运动速度在整个速度区间内不断增加时，与LSSVR以及PSO-LSSVR定位算法相比，本文提出的IPSO-LSSVR算法存在一定的优势。

图6 定位误差随测距误差增长的变化曲线Fig.6 Changing curve of localization error with range error increasing

图7 定位误差随速度增长的变化曲线Fig.7 Changing curve of localization error with speed increasing

4.4 算法稳定性分析

在移动节点定位过程中，定位算法的稳定性同样是对其进行评价的重要指标。因此，仿真时设置未知节点的初始坐标为(20, 20)，并且以1 m/s的速度沿X轴正方向做匀速直线运动。随着时间的推移，比较3种算法平均定位误差的变化情况，所得的仿真结果如图8。根据各个时刻3种算法平均定位误差的波动情况，发现LSSVR与PSO-LSSVR算法平均定位误差的浮动较大，表明这2种算法定位的稳定性有待加强，而本文提出的IPSO-LSSVR算法的定位误差曲线波动较小，稳定性较好。论文采用改进粒子群算法优化回归模型的正规化参数以及核函数参数，通过对PSO算法中的惯性权重和学习因子进行自适应调整，以及适应度函数的合理构造，降低了粒子种群陷入局部寻优的可能性，从而获得最优的模型参数，使得定位模型的拟合性能更好、抗噪能力更强，提高了算法的定位精度，增强了其稳定性。

图8 定位误差随时间增长的变化曲线Fig.8 Changing curve of localization error with time increasing

4.5 算法实时性分析

定位时间指一次定位的完成所消耗的时间，是评价移动节点定位算法的又一个重要标准，定位的时间越短，定位的实时性越好。为了衡量定位算法的实时性，表1中显示了3种算法的平均定位时间的估计值。从表1中不难发现，3种算法的平均定位时间均在0.15 s左右，其定位时间相差不大，在可接受的范围内，同时在定位算法的运行时间内，节点运动的距离相对较小，产生的误差基本可以忽略。由于回归模型的参数优化是在离线过程中进行的，因此，并没有增加实际过程中的定位时间，可以满足移动节点定位的实时性需求。

表1 定位算法的运行时间

5 结束语

移动节点定位作为物联网领域的热点问题之一，具有极强的研究价值。本文采用围栏定位方法，针对测量节点固定而未知节点以一定速度在定位区域内移动的情况，提出了一种改进粒子群算法优化LSSVR模型的移动节点定位方法。该算法首先通过对样本集进行训练获得LSSVR定位模型，然后自适应调整粒子群算法的惯性权重以及学习因子，降低陷入局部寻优的可能性，并将其应用于定位模型的参数优化。最后，将根据RSSI测距技术获得的节点移动过程中的距离向量输入到回归模型，得到未知节点的估计位置。仿真结果表明，与其他定位算法相比，本文提出的算法在满足移动节点定位实时性的同时，定位精度和稳定性都得到提高，表现出良好的定位性能。