论高中数学解题中代换法的应用

丁多利

(安徽省淮南市第二十一中学 232082)

高中数学中的代换类型较多，包括参数与常量之间的代换、参数之间的代换、参数与公式之间的代换等.代换法之所以能够进行，关键在于两者之间存在着数或逻辑上的相等关系.教学中为加深学生对代换法的深刻认识，牢固的掌握最重要的解题方法，应做好应用代换法解题的教学.

一、三角变换中代换法的应用

高中数学涉及很多三角恒等变换公式，如cos(α-β)=cosαcosβ+sinαsinβ、sin2α=2sinαcosα、cos2α+cos2α=1等，这些公式是进行代换的重要依据，因此，教学中应对三角恒等变换公式进行分类，要求学生采用对比法牢固的记忆，避免张冠李戴.同时，结合授课经验，优选经典的例题，与学生一起剖析解题过程，使学生能够掌握代换法的切入点，实现高效解题.

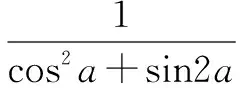
该习题属于三角函数中较为常规的题目，难度并不大.教学中引导学生认真分析要求了解分式的特点，积极联系所学知识进行合理的代换.如要求解分式的分子为1,很容易联想到cos2α+cos2α=1，通过代换后，则可转化为齐次式便可求解.

正确选项为C.

教学中通过引导学生分析该题目，使其认识到在解答三角函数相关的问题时一定不要忘记使用cos2α+cos2α=1进行代换.

二、常规函数中代换法的应用

对常规函数而言奇、偶函数、周期函数等存在等量关系，如f(x)=-f(-x)、f(x)=f(x+T)(T为周期)等.为使学生能够灵活运用常规函数中的等量关系进行巧妙的代换，顺利解答相关题目，应结合自身的教学经验设计代表性的问题，要求学生在课堂上思考解答，并做好解题经验总结，在以后的学习中遇到类似的问题，能够迅速的破题.

例2已知f(x)，g(x)分别是定义在R上的偶函数与奇函数，且f(x)-g(x)=x3+x2+1，则f(1)+g(1)=( ).

A.-3 B.-1 C.1 D.3

该题目难度并不大，解题的关键能够通过代换构建已知条件和要求解问题的关联.因为f(x)为偶函数，g(x)为奇函数，即，f(x)=f(-x)，g(x)=-g(-x)，显然可使用f(-x)-g(-x)代换f(x)+g(x).则可推出f(1)+g(1)=f(-1)-g(-1)，又因为f(x)-g(x)=x3+x2+1，则将x=-1代入f(-1)-g(-1)=-1+1+1=1，正确选项为C.

通过做该问题的求解使学生认识到，为顺利解答常规函数问题应注重常用等量关系的积累，并深刻理解，结合具体问题进行合理的变形与代换.

三、导数问题中代换法的应用

导数是高中数学的重要知识点，与其他知识联系紧密.部分习题常与基本不等式知识结合起来.解题时需要具体问题具体分析，巧妙的借助等量关系进行代换.教学中为提高学生运用代换法解答导数问题的意识，在解题中少走弯路，应注重为学生详细的讲解相关的例题，认真板书解题步骤，使其掌握代换法解题的相关细节.

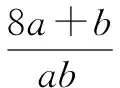
该题目是导数与不等式的结合习题，解题时需要从已知条件中挖掘隐含条件，而后通过等量代换，运用基本不等式公式进行求解.

又因为f′(1)=2a+b=2.

=5+4=9

当且仅当4a=b时，取“=”，因此，正确选项为B.

在课堂上为学生讲解该例题，使学生认识到“1”这一特殊的代换媒介，任何一个数或公式均可以看作其与“1”的乘积，或者分母为“1”，而后寻找与“1”相关的等量关系进行代换解题.

四、数列问题中代换法的应用

高中数学中还有一种特殊的代换关系，即，参数与公式间的代换.该代换关系虽然不难理解，但具有一定的技巧性.很多学生常因不会应用代换法而不能顺利的解答出相关习题，因此教学中应注重向学生展示相关的习题，并给予学生解题的引导，使其能够及时找到代换的突破口.

例4在等比数列{an}中，a1=2，a8=4，函数f(x)=x·(x-a1)·(x-a2)……(x-a8)，则f′(0)=( ).

A.26B.29C.212D.215

该题目数列与函数的综合题目，具有一定的技巧性，很多学生看到该题目后不知所措，事实上采用整体代换问题便可迎刃而解.令g(x)=(x-a1)·(x-a2)……(x-a8)，则f(x)=x·g(x)，则由导数知识可得f′(x)=g(x)+xg′(x)，则f′(0)=g(0)=(a1·a8)4=212，正确选项为C.

通过该习题的解答，使学生认识到解题时应认真观察给出的已知条件，构建参数与公式之间的等量关系，注重运用代换法进行解答.

高中数学部分习题应用代换法求解，可获得事半功倍的效果，因此教学中应做好这一重要方法的讲解，尤其围绕具体内容，选择不同类型的习题，为学生讲解带换法的具体应用，使其通过学习总结代换法的应用规律，充分把握其本质，在解题中做到游刃有余.