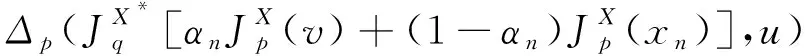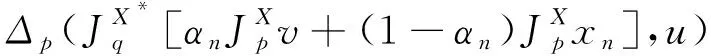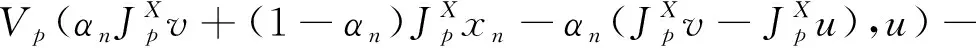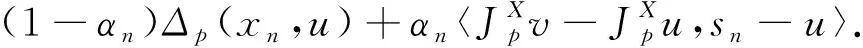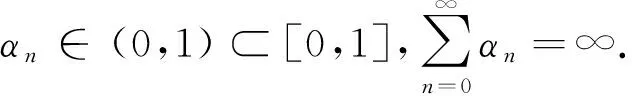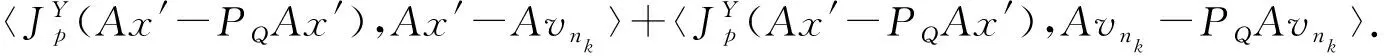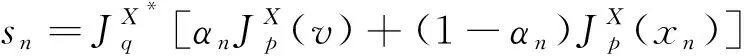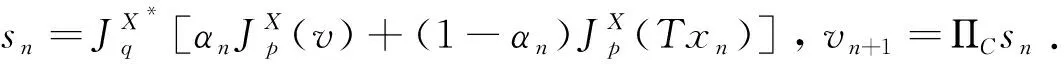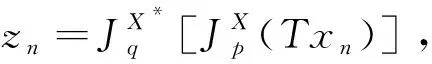Banach空间中分裂可行性和不动点问题的强收敛性

徐亚军 倪仁兴

(绍兴文理学院 数理信息学院，浙江 绍兴 312000)

1 文献综述

分裂可行性问题(SFP)是一个重要的非线性问题,它在一定条件下可与变分不等式问题(VIP)、不动点问题(FPP)等数学问题相互转化.SFP广泛应用于各种实际问题,如强放射治疗、信号处理和图像重建等问题.其研究成果已引起国内外学者们的高度重视[1].1994年, Censor和Elfving[2]两位学者首先在有限维Hilbert中提出SFP.虽然他们用多重投影法得到求解该问题的一个迭代序列,但是在每次迭代中都需计算矩阵的逆,使得计算变得复杂和困难.为了克服这一不足,Byrne[3]在2002年提出C—Q算法(梯度投影法).此后,C—Q算法成为一种研究SFP的主要方法.关于求解SFP的一些方法可参考文献[4-6].

非线性算子不动点迭代的早期成果是1922年Banach[7]提出的压缩映像原理.1953年,Mann[8]受Banach压缩映像原理的启发,提出了Mann迭代算法.1967年,Halpern[9]提出了Halpern迭代算法.1974年,Ishikawa[10]基于Mann迭代算法提出了两步迭代(Ishikawa迭代)算法.除此之外,还有许多基于这几种算法的其他算法[2-6].近几年来,人们对于非线性映射不动点的迭代计算越来越感兴趣[11-13].此外,还有许多学者在无穷维Hilbert空间中研究SFP[14-16].

以上文献中得到的许多结果都是建立在实Hilbert空间中.然而,在现实生活中多数数学问题都存在于Banach空间中.Banach空间比Hilbert空间更普遍.因此,在Banach空间中研究本课题十分有意义.到目前为止,在Hilbert空间中研究SFP解的强弱收敛定理已有较好的结果,但在一般Banach空间框架下的研究还较少.这是因为其研究相对较为困难,在Hilbert空间中一些性质在Banach空间中不再成立,如Hilbert空间中投影算子具有1-Lipschitz连续,正规对偶算子为恒等算子等性质.因此在Hilbert空间中处理分裂不动点问题的方法,一般并不适用于一般Banach空间.

最近,一些学者开始在Banach空间中研究SFP和FPP[17-19].值得指出的是,在文献[17]中,SFP的求解方法被推广到Bregman投影的情况下,Schopfer等人在p一致光滑的Banach空间X中引入了改进的C-Q算法,在X的对偶映射是弱到弱连续条件下,得到了弱收敛结果.本文的目的是在前人的基础上,利用Bregman投影构造一类迭代算法,用来逼近SFP的解.它同样也是左Bregman强非扩张映像的不动点,并得到了强收敛的结果.本文的扩展改进和完善了以上文献中的相关研究结果.

2 预备知识

本节主要回顾了度量投影,Bregman投影,左Bregman强非扩张映像等定义,给出了有关Bregman投影的一些性质,并且讨论在后续内容中会使用到的相关引理.

定义2.1[20]设f:E→R是一Gteaux可微的凸函数.关于f的Bregman距离定义为:

Δf(x,y)=f(y)-f(x)-(f′(x),y-x),∀x,y∈E

(2.1)

定义2.2[21]设非线性算子T:C→C,算子T的渐进不动点集定义如下:

(2.2)

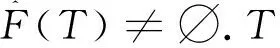
(2.3)

(2.4)

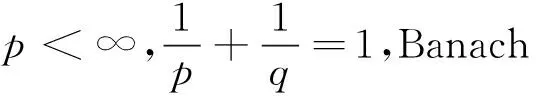
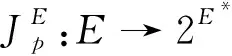
特别地,在p一致凸Banach空间中,度量和Bregman距离有下列关系[21]:

(2.5)

其中τ>0是一固定的数.

定义2.5[18]设C是Banach空间E的非空闭凸子集,度量投影定义为:

它是范数距离的唯一最小点,它可由下列变分不等式(VI)来表征:

(2.6)

类似于度量投影,Bregman投影定义如下:

它是Bregman距离的唯一最小点,同样,Bregman投影可以用下列变分不等式(VI)来表征:

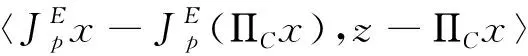
(2.7)

由上式得

Δp(ΠCx,z)≤Δp(x,z)-Δp(x,ΠCx),∀z∈C

(2.8)

根据文献[22],定义函数Vp:E*×E→[0,+∞)如下：

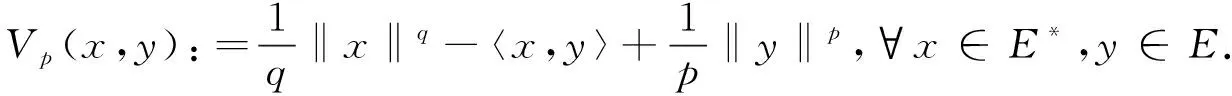
〈f′(x),y-x〉≤f(y)-f(x).

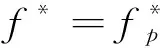
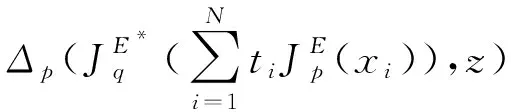
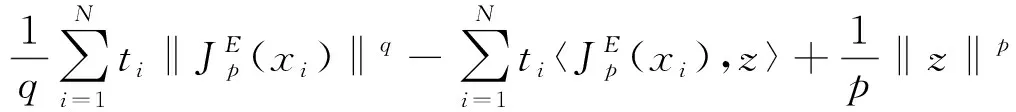
(2.10)

接下来的引理2.1,引理2.2和引理2.3在本文主要结果的证明中起到重要作用.

引理2.1[23]设E是q一致光滑的,x,y∈E,则存在mq>0,使得

‖x-y‖q≤‖x‖q-q〈Jp(x),y〉+mq‖y‖q.

引理2.2[24]设{an}是一个非负实数列，满足下列关系：

an+1≤(1-αn)an+αnσn+rn,

其中，(i){αn}⊂[0,1],∑αn=∞;(ii)limsupσn≤0;(iii)γn≥0,∑γn<∞.

则有an→0,n→∞.

引理2.3[25]设{an}是一个实数列,使得存在{n}的一个子列{ni},满足ani

amk≤amk+1,ak≤amk+1.

事实上,令mk=max{j≤k:aj

2015年,Shehu,Ogbuisi和Iyiola在文献[1]中,得到如下主要结果:

(2.11)

通过以上结论,很自然地能产生如下一个问题A:当迭代参数序列{θn}取θn≡1或θn≡0时,以上定理是否还成立?

3 主要结果—定理3.1和定理3.2及其证明

本节的目的是给出问题A的一个肯定回答.因此,得到以下两个定理:定理3.1和定理3.2.

(3.1)

(3.2)

下面分别给出定理3.1和定理3.2的证明.

证明记rn=Avn-PQ(Avn),由(2.7),对于∀u∈F(T)∩Γ,可得

(3.3)

这样由(3.3)和引理2.1可以得到

(3.4)

根据条件(iii),得到

Δp(xn,u)≤Δp(vn,u).

(3.5)

根据(2.8),(2.10)和(3.5)可得

≤αnΔp(v,u)+(1-αn)Δp(xn,u)

≤αnΔp(v,u)+(1-αn)Δp(vn,u)

≤max{Δp(v,u),Δp(vn,u)}

≤⋮

≤max{Δp(v,u),Δp(v1,u)}

(3.6)

情形1假设序列{Δp(xn,u)}单调非增,即存在n1∈N,使得{Δp(xn,u)}是单调增的.又因为序列{Δp(xn,u)}的非负性,根据单调有界定理知序列{Δp(xn,u)}是收敛的且

Δp(xn+1,u)-Δp(xn,u)→0,n→∞.

(3.7)

Δp(wn,ΠC(wn))≤Δp(wn,u)-Δp(xn,u)

≤Δp(vn,u)-Δp(xn,u)

(3.8)

≤αn-1L+Δp(xn-1,u)-Δp(xn,u)→0,n→∞.

(3.9)

同样地,由(3.4)知

(3.10)

(3.11)

(3.12)

由A的连续性,‖xn-vn‖→0可得xnk⇀Ax′,Avnk⇀Ax′.在(3.12)中令k→∞,可得‖Ax′-PQAx′‖=0.因此,Ax′=PQAx′,即Ax′∈Q.故证明了x′∈Γ.

Δp(sn,xn)≤αnΔp(v,xn)+(1-αn)Δp(xn,xn)→0,n→∞.

(3.13)

情形2 假设存在{n}的子列{nk},使得Δp(xnk,u)<Δp(xnk+1,u),∀k∈N.由引理2.3知存在一个非递减的序列{mk}⊂N,使得Δp(xmk,u)≤Δp(xmk+1,u)和Δp(xk,u)≤Δp(xmk+1,u).由单调有界定理知序列{Δp(xmk,u)}收敛.

综上所述,证明了文献[1]得到的主要结果:定理2.1[1]中的参数θn≡1时,由算法(2.11)生成的序列{xn}和序列{vn}都强收敛到x0=ΠΓ(v).

证明证明x′∈Γ过程同定理3.1的证明类似.此处不再证明.

Δp(zn,u)=Δp(Txn,u)≤Δp(xn,u).

(3.14)

因此,根据(2.10),(3.5)和(3.14)可得

(3.15)

下证xn→ΠF(T)∩Γ(v).记x0=ΠF(T)∩Γ(v),类似(3.6)证明得

接下来的证明过程与定理3.1中两种情形,情形1和情形2类似,不再详细证明.

综上,我们证明了文献[1]得到的主要结果:定理2.1[1]中参数θn≡0时,由算法(2.11)生成的序列{xn}和序列{vn}都强收敛到x0=ΠF(T)∩Γ(v).

注3.1定理3.1和定理3.2分别说明了文献[1]得到的主要结果:定理2.1[1]对θn≡1和θn≡0均成立.因此,我们的主要结果—定理3.1和定理3.2是对2015年Shehu,Ogbuisi和Iyiola[1]的主要结果—定理2.1[1]的拓展和补充.