基于时空效应的临河深基坑地表沉降规律分析

张 猛 陈 斌

(1.绍兴文理学院 土木工程学院，浙江 绍兴 312000；2.宁波工程学院 建筑与交通工程学院，浙江 宁波 315211;3.宁波市轨道交通集团有限公司，浙江 宁波 315101)

0 引言

基坑工程的“时空效应”是指在施工过程中，支护结构及周边土体变形随施工周期、坑底无支撑暴露时间、开挖空间尺度和深度的变化而发展的理论，特别是在软土地区，当深基坑临近河流湖泊时，使得地质条件更加复杂，开挖过程中的时空效应也变得更为明显.

有众多学者针对软土地区深基坑施工阶段时空效应变化规律开展了大量研究.刘建航等[1]结合上海基坑工程，提出了考虑时空效应预测围护结构内力计算的理论和方法.Wang等[2]收集了不同支护形式的基坑监测数据，分析得到了基坑的最大侧移及地表最大沉降的规律.刘爱华等[3]采用时空效应理论中的分区间、分时段等有效措施控制和减小了土体产生的最大位移.黄珏皓等[4]对宁波某基坑开挖过程进行模拟，分析在时间效应理论下支护结构的变形特点.胡之锋等[5]分析了某地铁基坑钢支撑滞后架设导致坑底无支撑暴露时间过长对地表沉降的影响规律.李伟[6]结合上海某地铁基坑现场监测数据，分析了沉降主要发生在土方开挖的过程中,且施工中时空效应较明显.

目前，针对软土地区临河深基坑基于时空效应的地表沉降变化规律研究较少，缺乏工程经验.本文以宁波市轨道交通5号线一期工程兴庄路站为工程背景，对软土地区临河深基坑进行重点分析，辅以对比5号线一期工程类似地质条件的非临河深基坑下应路站，从时间、空间角度，重点分析在开挖过程中，地表沉降监测点的变形发展规律及分析临河因素对地表沉降的影响.

1 工程概况

1.1 项目概况

宁波市轨道交通5号线一期工程兴庄路站为地下二层岛式车站，总体分二期施工，一期施工东基坑，二期施工西基坑.本文结合东基坑现场监测数据，重点分析地表沉降监测点的变形发展规律.

东基坑采用明挖顺作法施工，标准段深度16.5 m，端头井深度18.0 m.围护结构采用800 mm厚地下连续墙，标准段采用1道砼支撑+4道钢支撑，端头井采用1道砼支撑+5道钢支撑.标准段地连墙插入比为1.07，端头井插入比为1.14.标准段支撑横断面及参数见图1.

兴庄路站北侧为大叶界河，因主体结构距离河道最近约1.2 m(围堰后距离为7.5 m)，且河流宽度约15 m～20 m， 河水位一般低于地面0.0 m～2.0 m，水深约2.0 m，浮泥厚度约0.3 m～0.6 m.主体结构与大叶界河相对位置见图2.

1.2 地质条件

宁波软土具有高含水量、高孔隙比、高流变性、压缩性大、渗透性差等特点，这点与其他地区的软土特征相同，差别在于宁波软土抗剪强度变化范围更大[7].基坑开挖影响涉及土层主要物理力学参数详见表1.

表1 主要物理力学参数表

1.3 现场监测

东基坑全长约103 m，主体结构按照每块25 m左右，划分为4块，开挖采用分层分段从两端向中间开挖.

现将东基坑标准段施工过程分为九个工况，详见表2.由于现场监测数据是从架设完第一道砼支撑之后开始采集，因此没有工况一的变形曲线.东基坑监测平面图见图3.

表2 标准段工况概述表

2 地表沉降规律时空效应分析

深基坑本身是具有平面尺寸和立面深度的三维空间结构，加上时间的影响作用，可将开挖过程看成四维空间问题.基坑开挖破坏原有稳定状态，坑内外产生压力差，导致围护结构产生向坑内挤压移动态势，进而产生位移.同时围护结构的变形会导致周围土体应力发生重分布，在土体自重、软土流塑性的影响下，致使坑内外土体产生向下发展趋势，最终发生地表沉降[8].地表沉降在有无地面超载的情况下，变形特征迥异，同时由于主体结构靠近河流，临河因素可能主要由于软土层埋深的变化以及非对称荷载的作用影响围护结构顶端位移，进而影响地表沉降变化.

根据兴庄路站地表沉降监测点布设情况，选取代表性测点对深基坑地表沉降随时间、空间变化规律进行分析.

2.1 地表沉降随时间变化规律分析

临河侧地表沉降监测点(D1～D6)由于靠近大叶界河，因此垂直基坑走向只布设2组测点，非临河侧地表沉降监测点(D48～D55)垂直基坑走向均布设5组，测点间距分别为4 m、9 m、12 m、12 m、15 m，其中第一个间距是指首个测点距基坑主体结构的距离.结合测点布设情况，选取临河侧端头井D1测点、临河侧标准段中部D3测点及背河侧标准段中部D51测点进行分析，图4为地表沉降随时间变化图.

综上所述，对肺癌合并糖尿病患者实施目标性护理服务有助于降低手术风险事件发生，有助于提高患者的临床疗效、预后康复效果，保持血糖稳定，应用效果良好。

由图4可以看出：(1)开挖初期，地表沉降值变化较小，分析原因主要是第一道砼支撑及相邻钢支撑的约束.(2)随开挖的持续进行，除距离基坑较远处的D51-5测点外，其余测点沉降绝对值均不断变大.(3)沉降变化随底板浇筑完成形成强度可分为前后两部分.在施工进行到工况五时，随着第五道支撑的架设及结构底板的施作，施作时间较长，导致坑底无支撑暴露时间较长，这一阶段地表沉降速率明显变大，表现出明显的时间效应，到工况六底板浇筑完成，地表沉降速率逐渐变缓.

为进一步分析地表沉降基于时间效应的变化规律，对各个地表沉降监测点在不同工况下的沉降最大值进行拟合分析，拟合曲线图见图5.结合现场实测数据，可将地表沉降最大值发展模式拟合为多项式函数方式，表达式为：

y=0.008 3x2-2.134 2x+29.069 8

(1)

式中：x—开挖天数(d)；y—不同工况下地表沉降最大值(mm).

相关度R2=0.992 6，对比参考文献[4]中R2=0.990，本文拟合效果更好.从图5中可以看出，随工况的持续进行，地表沉降变化持续增大，在工况五、工况六底板施作过程中，地表沉降速率较快，占开挖阶段总变形比例也较大，底板的施作完成及产生强度后，地表沉降速率明显减小.基于上述现象，在保证底板强度的前提下，应尽量加快底板施工速度，减少坑底无支撑暴露时间，并通过减少周围施工扰动进一步约束围护结构变形，从而减小地表沉降.

2.2 地表沉降随空间变化规律分析

开挖过程中，平面尺寸、立面深度的大小都将影响主体结构本身及周边环境的变形.采用同济启明星深基坑支挡结构设计计算软件FRWS 7.0对围护结构分析计算.选取东基坑标准段进行分析，主动侧土压力采用朗肯主动土压力，被动侧基床系数采用“m”法计算，地面超载取20.0 kPa，地表沉降采用同济抛物线法计算，计算方法如下：

地表沉降范围：

x0=(H+D)·tg(45°-φ/2)

(2)

地表最大沉降：

(3)

Δδ=0.5(δw1+δw2)

(4)

各点沉降：

(5)

式中：H—开挖深度(m)；D—开挖面以下围护结构长度(m)；φ—土层内摩擦角；Sw—围护结构侧移面积(m2)；x—与基坑间距(m)；δw1、δw2—围护结构顶、底端位移(mm).

由上述计算公式可知，地表沉降值不仅与开挖深度、围护结构深度有关，还与围护结构位移有关.

在陈斌[9]统计的宁波轨道交通1、2号线13个车站基坑实测数据的基础上，加上本文前面分析的兴庄路站、下应路站实测数据，对地表沉降变形规律进行统计分析.

图6为统计的15个站点地表沉降最大值δvm与开挖深度H之间的关系图.由图6可以看出，δvm落于0.13%H与1.2%H之间，平均值为0.72%H.本次统计结果大于朱瑶宏[10]统计的宁波地区平均值(介于0.15%H～1.2%H，平均值约为0.69%H)，但差距仅为0.03%.

图7为统计的15个站点地表沉降最大值δvm与围护结构平均最大水平位移δhm之间的关系图.由图7可以看出，δvm落于0.6δhm与3.07δhm之间，平均值为1.67δhm.统计结果小于朱瑶宏[10]统计的宁波地区平均值(基本介于0.6δhm～3.07δhm，平均值约为1.72δhm).由统计结果对比可知，兴庄路站与下应路站对地表沉降的控制均较好，且兴庄路站控制效果好于下应路站.

为进一步分析地表沉降基于空间效应的变化规律，通过软件得到的设计计算位移、弯矩、剪力以及地表沉降结果图见图8.

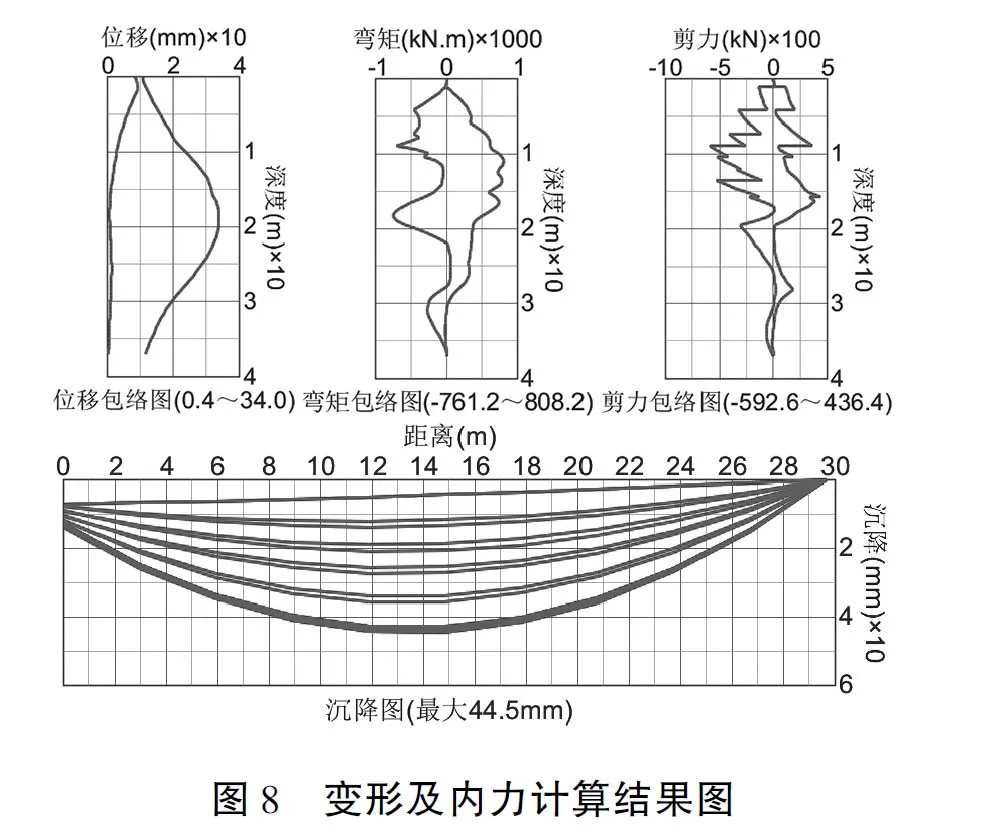
结合实测值与计算值对比可知：实测变形值远大于相应位置计算值，分析原因是软件计算时建立的是二维模型，未考虑随基坑开挖尺寸变化、拐角变化对变形的影响，同时围护结构变形时未考虑土压力持续发展时间效应.

选取地表沉降监测点D1、D3、D51，绘制地表沉降在不同工况下的变化图,见图9.

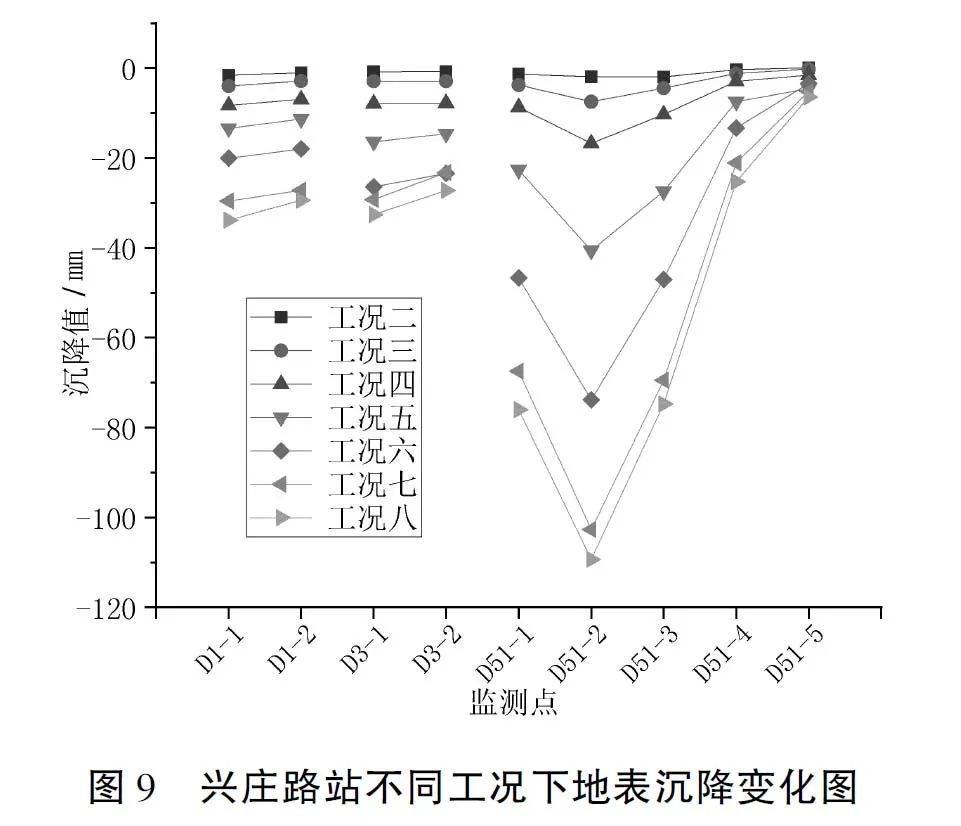
结合图9及地表沉降监测点位置可知：(1)背河侧标准段中部D51测点相较于临河侧端头井D1测点、临河侧标准段中部D3测点，D51测点沉降值最大，且最大值出现在距离基坑13 m处的D51-2处，最大值出现位置约为0.75 H，沉降值大于报警值.(2)背河侧沉降值明显比临河侧沉降值大.结合现场监测数据得出的临河侧标准段中部测斜点CX03围护结构最大水平位移为70.9 mm，背河侧标准段中部测斜点CX49最大水平位移为82.7 mm，分析出现两侧沉降差异的主要原因为，临河侧周边荷载较小，背河侧是住宅小区及城市道路，存在车辆、人群等不确定荷载，使得背河侧围护结构变形较大，从而导致背河侧地表沉降值增大.

2.3 临河因素对地表沉降影响分析

根据5号线一期工程类似地质条件的非临河深基坑下应路站实测数据，绘制不同工况下地表沉降变化图见图10，下面对比两个车站的监测数据来分析临河因素对地表沉降的影响规律.

选取下应路站北侧端头井D1测点、北侧标准段中部D6测点及南侧标准段中部D18测点.因兴庄路站大叶界河距主体结构最近距离仅1 m左右，临河侧地表沉降监测点垂直基坑走向只布设2组，其余侧均布设5组，下应路站测点均布设6组.

对比图9、图10可知：(1)除临河侧测点外，其余测点地表沉降最大值出现位置约为0.75 H，沉降变形曲线呈现“凹槽形”.(2)兴庄路站临河侧因河流对土体应力释放作用，以及临河侧外荷载较少、对基坑扰动小，地表沉降值明显小于背河侧，且沉降曲线并非呈传统“凹槽形”，而是随着与坑边距离的增大而减小.(3)临河因素可能主要由于软土层埋深的改变影响围护结构顶端位移，进而影响地表沉降变化.

3 小结

本文结合宁波软土地区临河深基坑兴庄路站现场监测数据，重点对开挖过程中地表沉降的变化规律进行分析.主要结论如下：

(1)将不同工况下地表沉降最大值发展模式拟合为多项式函数方式，在结构底板施作过程中，地表沉降速率较快，占开挖阶段总变形比例也较大，结构底板的施作完成及产生强度后，地表沉降速率明显减小，体现出典型的时空效应.

(2)地表沉降值不仅与开挖深度、围护结构深度有关，还与围护结构位移有关.地表沉降最大值δvm与开挖深度关系约为0.72%H，与围护结构平均最大水平位移关系约为1.67δhm.

(3)临河侧地表沉降值明显小于背河侧，且沉降曲线并非呈传统“凹槽形”，而是随着与坑边距离的增大而减小.临河因素可能主要由于软土层埋深的改变影响围护结构顶端位移，进而影响地表沉降变化.

(4)针对软土深基坑工程，应在保证底板强度的前提下，尽量加快底板施工速度，减少坑底无支撑暴露时间，并通过减少周围施工扰动进一步约束围护结构变形，从而有效减小地表沉降变形，降低对周围环境的影响.