拉萨市近50年极端气温的时间特征分析

鲁同所，王红宾，雷 阳，傅文雪，廖偲含，卫 东

（1.西藏大学理学院，西藏拉萨850000；2.中国科学院上海应用物理研究所，上海 嘉定201800；3.拉萨市气象局，西藏 拉萨850000）

0 引言

极端天气气候事件简称极端气候事件，是指某一气候要素的统计值或量值在特定的地区和时间段内严重偏离其平均态的事件，在统计学意义上属于小概率事件.20世纪以来，随着全球气候不断变暖，极端气候事件发生的频率也明显上升，由气候变化所引起的一系列问题备受公众瞩目，极端气候事件的加剧，对人类的生存环境、社会经济的发展、区域的生态环境产生严重的破坏和影响，相对于平均气候变化，极端气候事件的变化对自然环境和人类社会的冲击强度更大.因此，众多学者围绕极端气候事件开展系列科学研究［1-6］.

拉萨，西藏自治区政治、经济、文化和科研中心，也是西藏自治区的首府所在地，地处青藏高原的中部，喜马拉雅山脉北侧，平均海拔高达3 650 m，气温昼夜温差大；空气稀薄，降雨稀少，太阳辐射量大，生态系统的抵抗力、恢复力极弱，对极端气候的变化反应极其敏感.众所周知，2019年6月25—29日，拉萨连续5日平均气温超过22℃，首次达到了我国气候季节划分的夏季标准，标志着拉萨自1955年有气象记录以来首次“成功入夏”.并且拉萨市在6月下旬出现了30.8℃的高温天气，不仅打破当地高温历史记录，还是其气象观测史上第二次出现30℃以上的气温，若放在平原地区，这已经相当于40℃以上的火热高温，这次史无前例的异常天气事件，可能和北半球西风带大幅振荡以及全球变暖影响青藏高原有关.遗憾的是，目前还没有学者对拉萨市的极端气温进行系统研究.因此，本文基于1970到2018年间拉萨市监测到的气温数据，对其极端天气气候事件的时间特征进行分析，也探究深层原因.由此，我们希望这项工作能为拉萨当地居民、援藏职工、旅游爱好者、科研工作者更好地适应当地生存环境提供一定的帮助，也可以为决策部门建立高温、低温预警机制，制定相应的对人群的保护和公共卫生措施，预防自然灾害、保护和改善当地的生态环境提供一定参考.

1 数据来源及研究方法

1.1 数据来源

为了确保研究数据的连续性和研究结果的可靠性，本文采用拉萨市气象站（全名：拉萨市国家基本气象局，该气象局位于拉萨市中心，探测范围囊括整个拉萨市区，是拉萨市建立最早、基础设备最完善的气象站点，同时拥有时段最长、最完整的探测数据）1970—2018年近50年逐日最高气温、最低气温和平均气温数据，并且所有数据均经数传组工作人员严格的质量检查，剔除少数错误值与异常值.

1.2 研究方法

1.2.1 极端气候指数

极端气候指数是由世界气象组织在气候变化监测会议中提出研究极端气候变化的一套标准方法，由逐日气温和逐日降水数据计算而得，具有弱极端性、噪声低、显著性强等特点.本文主要基于16个极端气候指数进行了分析，如表1所示［7］.

1.2.2 变量分析方法

首先，对于极端气候指数的变化趋势，采用回归系数法来研究气候要素在长时间变化过程中的升降趋势，回归系数的正负表示变量的上升或下降趋势，回归系数为正，则表明变量随时间的变化呈上升趋势，反之，则表明变量随时间的变化呈下降趋势，再选取线性方程对序列变量进行拟合得出相关系数，相关系数r表示变量与时间序列之间的关联程度.它消除了温度的均方差对线性回归系数大小的影响，可以用于研究不同区域位置温度之间的长期变化趋势［8］.

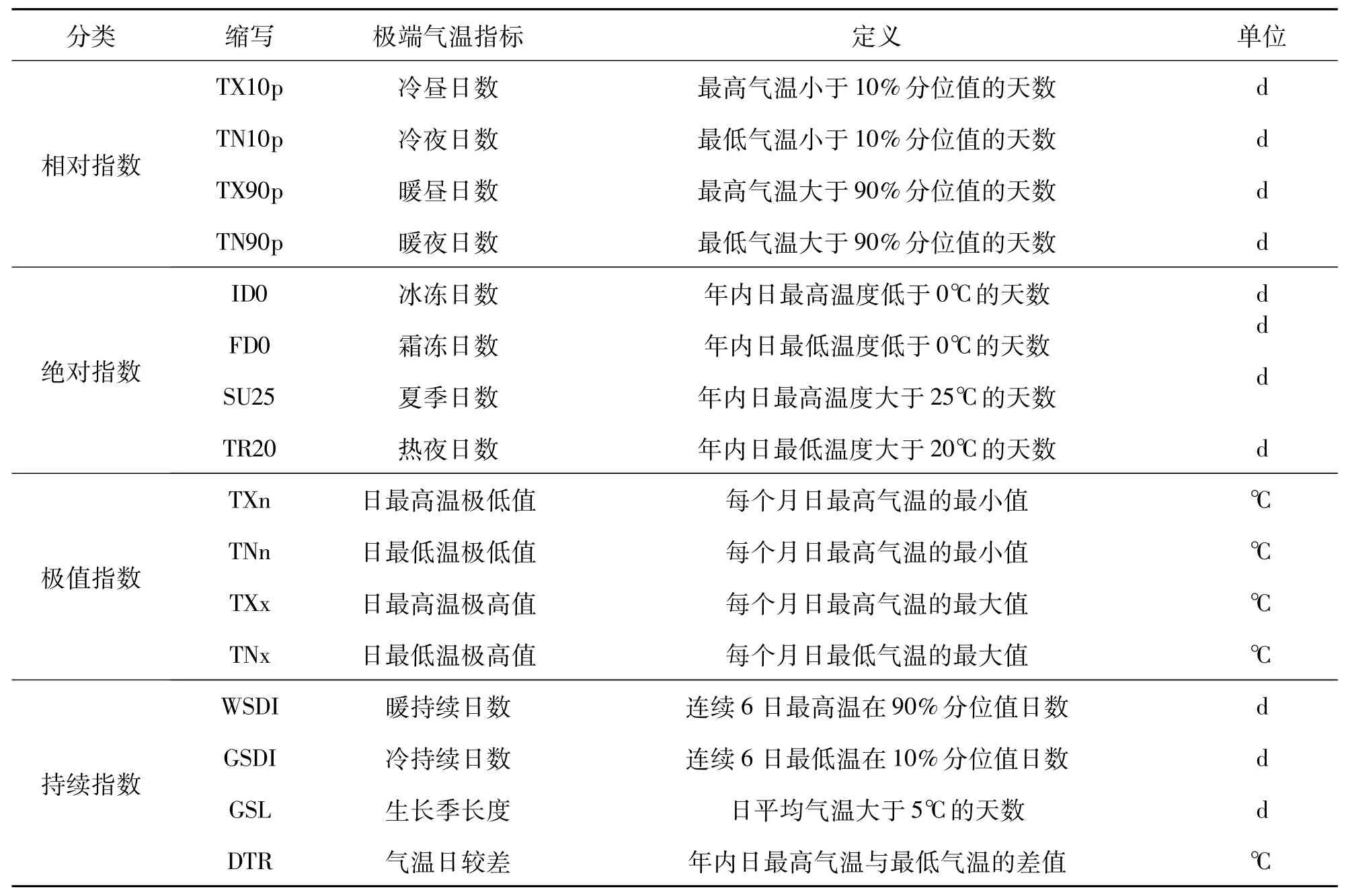
表1 极端气温指数定义Tab.1 Definition of extreme temperature index

其次，对于极端指数的突变节点，我们选用Mann-Kendall非参数检验法来确定变量随时间序列变化过程中的突变节点以及突变点前后的变化趋势，先选取显著性水平α=0.05，随后将UFK和UBK两条序列曲线与显著性水平α=0.05的临界线±1.96绘制在同一张图上，如果UFK和UBK的值大于0，则表明序列呈上升趋势，反之则表明序列呈下降趋势，当它们超过临界线时，表明上升或下降趋势显著，若UFK和UBK两条曲线出现交点，且交点在临界线之内，那么说明交点就是突变点，同时，此方法不需要样本数据遵循一定的分布规律，也不受少数异常值的影响，方便于计算［9］.

最后，为了得到极端最高、最低温度的变化周期，采用Morlet小波分析法对气温数据进行周期演变分析，并绘制小波变换等值线图和小波方差图，以此来反映气温在不同时间尺度的冷暖变化周期.相对于常规分析法而言，小波分析在时域、频域上具有很强的局部辨识力，可诊断出气温序列变化的多层次特征，从而得到周期变化在各个时间尺度上的详细信息［10］.

2 结果分析

2.1 极端气温指数时序变化趋势

为了研究拉萨市近50年来极端最高、最低气温和极端气温指数的变化趋势，我们对序列变量进行回归分析，由拉萨市极端气温相对指数（图1）、绝对指数（图2）、极值指数（图3）、持续指数（图4）的变化趋势图可以看出，近50年来拉萨市气温极值与其对应的极端气温事件变化特征明显，且波动较大，极端冷事件发生的频率随着时间序列的变化不断减小，而极端暖事件发生的频率恰恰与之相反.

由图5（a）和（b）知极端最高气温的变化总体呈波动上升趋势，极端最低气温的变化也呈现出波动上升趋势.极端最高气温的最大值为18.43℃，出现在2009年，最小值为14.71℃，出现在1978年，一元线性回归方程为：

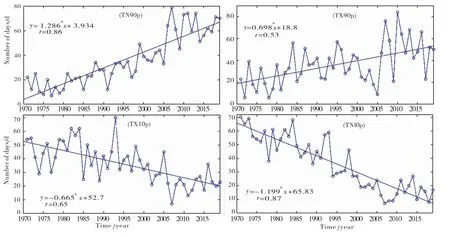
图1 拉萨市近50年极端气温相对指数变化趋势图Fig.1 Relative index change trend of extreme temperature during the recent 50 years in Lhasa

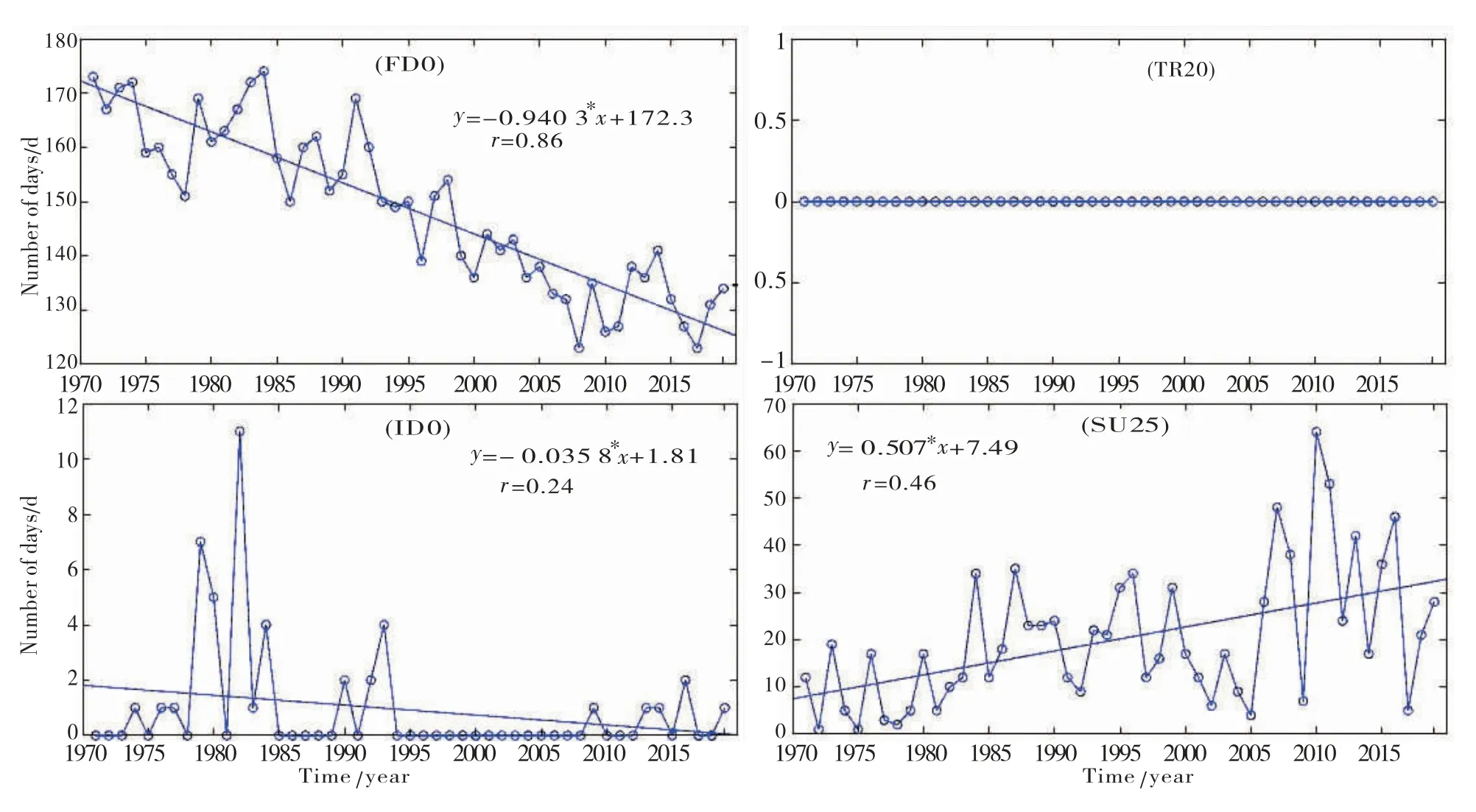
图2 拉萨市近50年极端气温绝对指数变化趋势图Fig.2 Absolute temperature index variation trend of extreme temperature during the recent 50 years in Lhasa

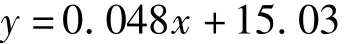
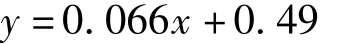
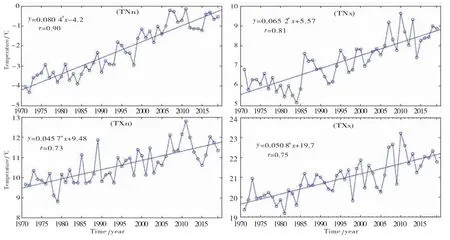
图3 拉萨市近50年极端气温极值指数变化趋势图Fig.3 Extreme index change trend of extreme temperature during the recent 50 years in Lhasa

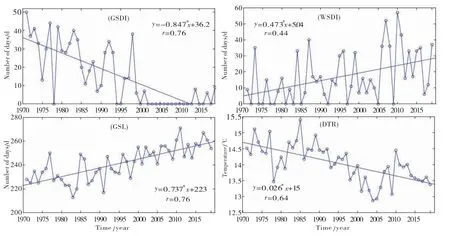
图4 拉萨市近50年极端气温持续指数变化趋势图Fig.4 Ongoing index variation trend of extreme temperature during the recent 50 years in Lhasa

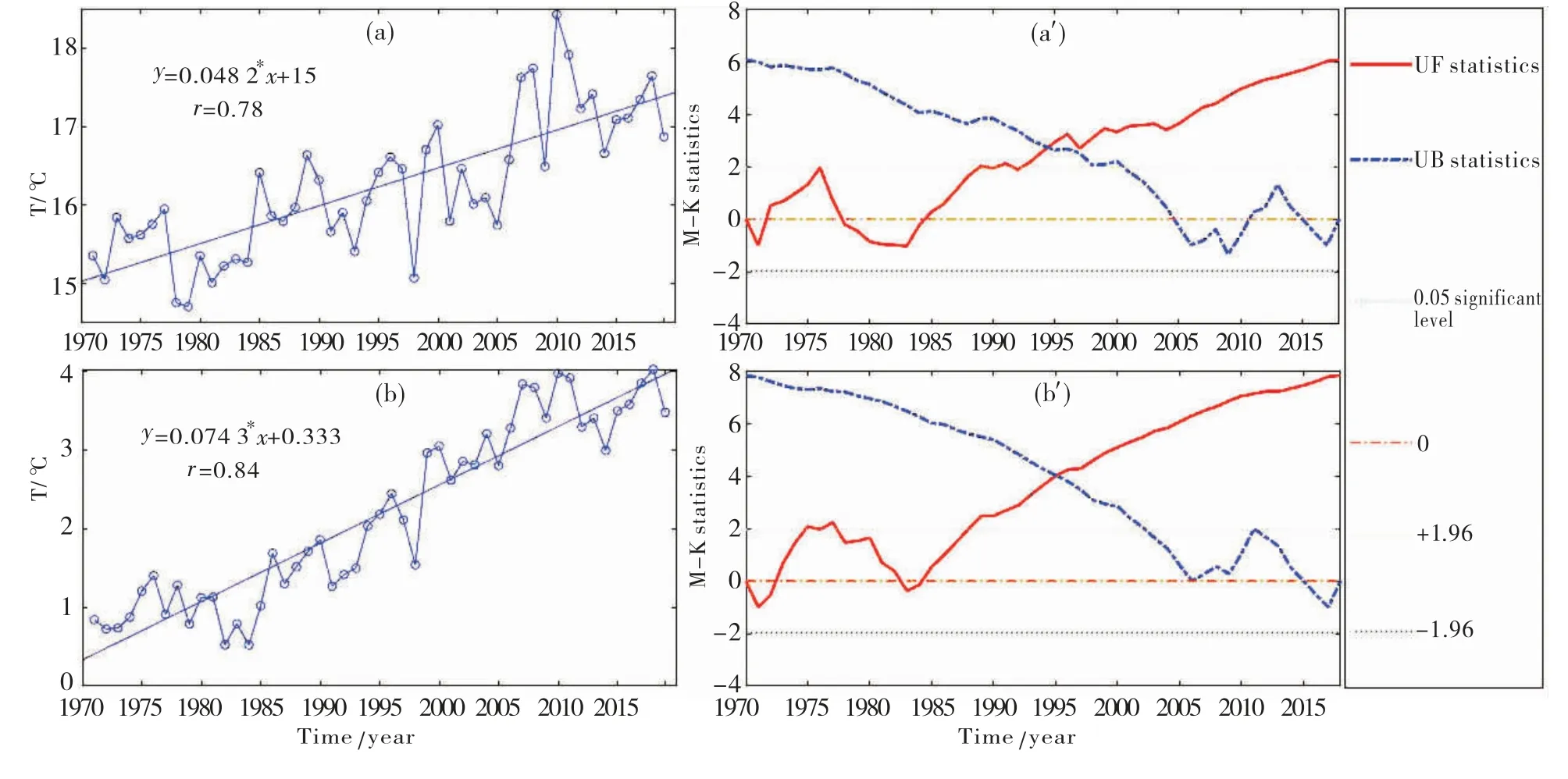
图5 拉萨市近50年日最低最高气温年平均变化趋势及Mann-Kendall检测曲线图［图a和a′表示日最高年平均，图b和b′表示日最低年平均］Fig.5 Annual average variation trend of the minimum and maximum temperature during the recent 50 years in Lhasa and the curve chart of Mann-Kendall mutation test［Fig.a and Fig.a′show the annual average value of daily maximum temperature，Fig.b and Fig.b′show the annual average value of daily minimum temperature］

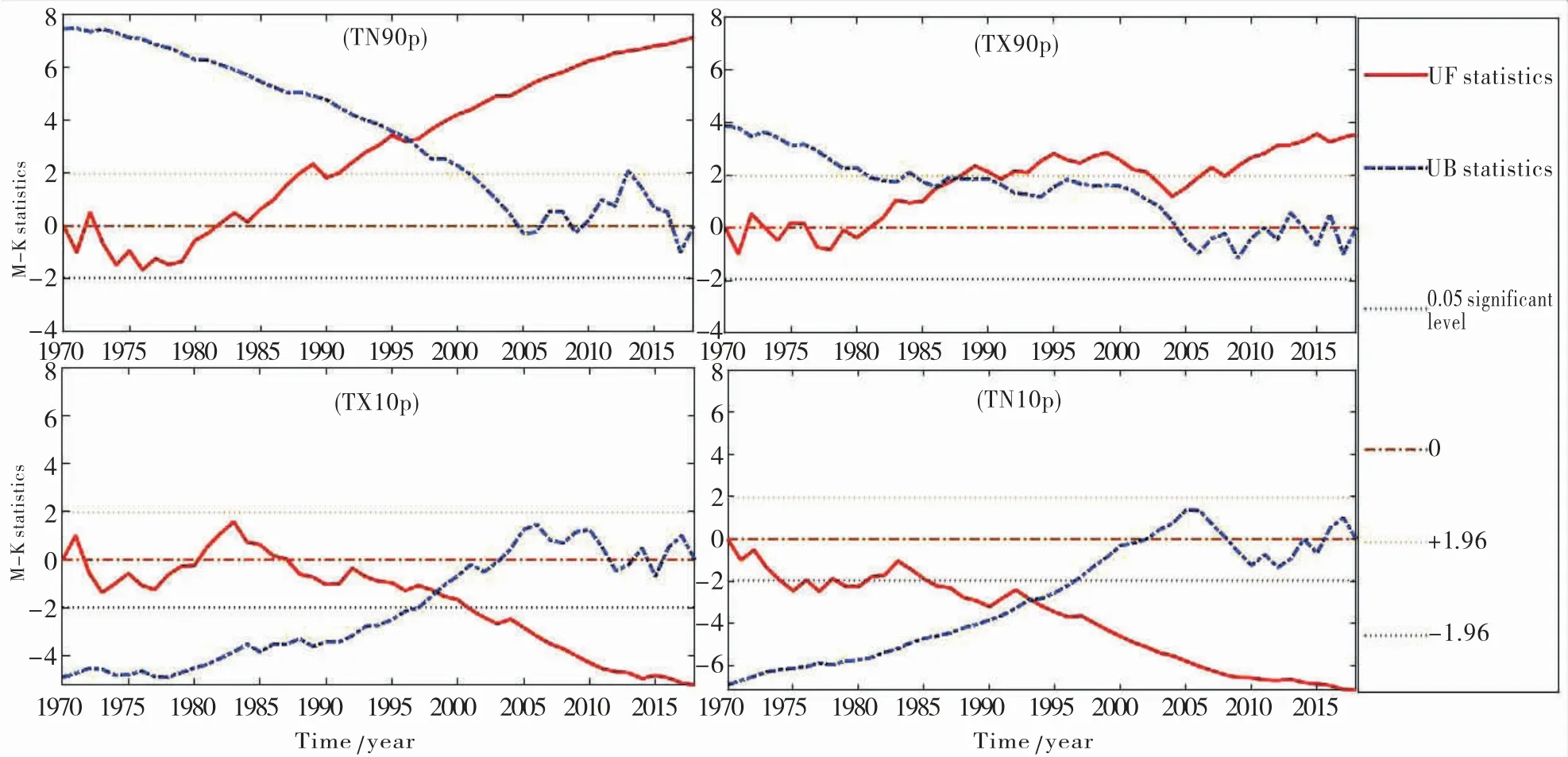
图6 拉萨市近50年极端气温相对指数Mann-Kendall检测曲线图Fig.6 Relative index curve chart of extreme temperature by means of Mann-Kendall mutation test during the recent 50 years in Lhasa

线性趋势变化率为0.48℃/10a（相当于0.048℃/a）.极端最低气温的最大值为4.03℃，出现在2017年，最小值为0.52℃，出现在1983年，一元线性回归方程为：线性趋势变化率为0.66℃/10a（相当于0.066℃/a），极端最高、最低气温的相关系数r分别为0.78、0.93，均通过了α=0.05的显著性检验，表明极端最高、最低气温的上升趋势显著.极端气温指数中冷昼日数TX10p、冷夜日数TN10p、霜冻日数FD0、冰冻日数ID0、冷持续日数GSDI、气温日较差DTR均呈现出下降趋势，下降趋势最显著的为TN10p、FD0、GSDI，下降极端气温指数的多年平均值分别为36.1 d、35.9 d、148.8 d、0.9 d、15.0 d、14.0℃，线性趋势变化率分别为-6.7 d/10a、-12.0 d/10a、-9.4 d/10a、-0.4 d/10a、-8.5 d/10a、-0.3℃/10a，相关系数r分别为0.65、0.86、0.86、0.24、0.76、0.64.暖夜日数TN90p、暖昼日数TX90p、夏季日数SU25、日最低气温极低值TNn、日最低气温极高值TNx、日最高气温极低值TXn、日最高气温极高值TXx、暖持续日数WSDI、生长季长度GSL均呈现出明显上升趋势，其中TN90p、TX90p、GSL、SU25上升趋势最为显著，上升极端气温指数的多年平均值分别为36.1 d、36.3 d、20.2 d、-2.2℃、7.2℃、10.6℃、20.9℃、16.8 d、241.3 d，线性趋势变化率分别为12.7 d/10a、7.0 d/10a、5.1d/10a、0.8℃/10a、0.7℃/10a、0.5℃/10a、0.5℃/10a、4.7 d/10a、7.4 d/10a，相关系数r分别为0.86、0.53、0.48、0.90、0.81、0.72、0.75、0.44、0.76，上述极端气温指数的相关系数均通过了α=0.05的显著性检验，表明极端气温指数上升或下降的趋势变化非常显著.

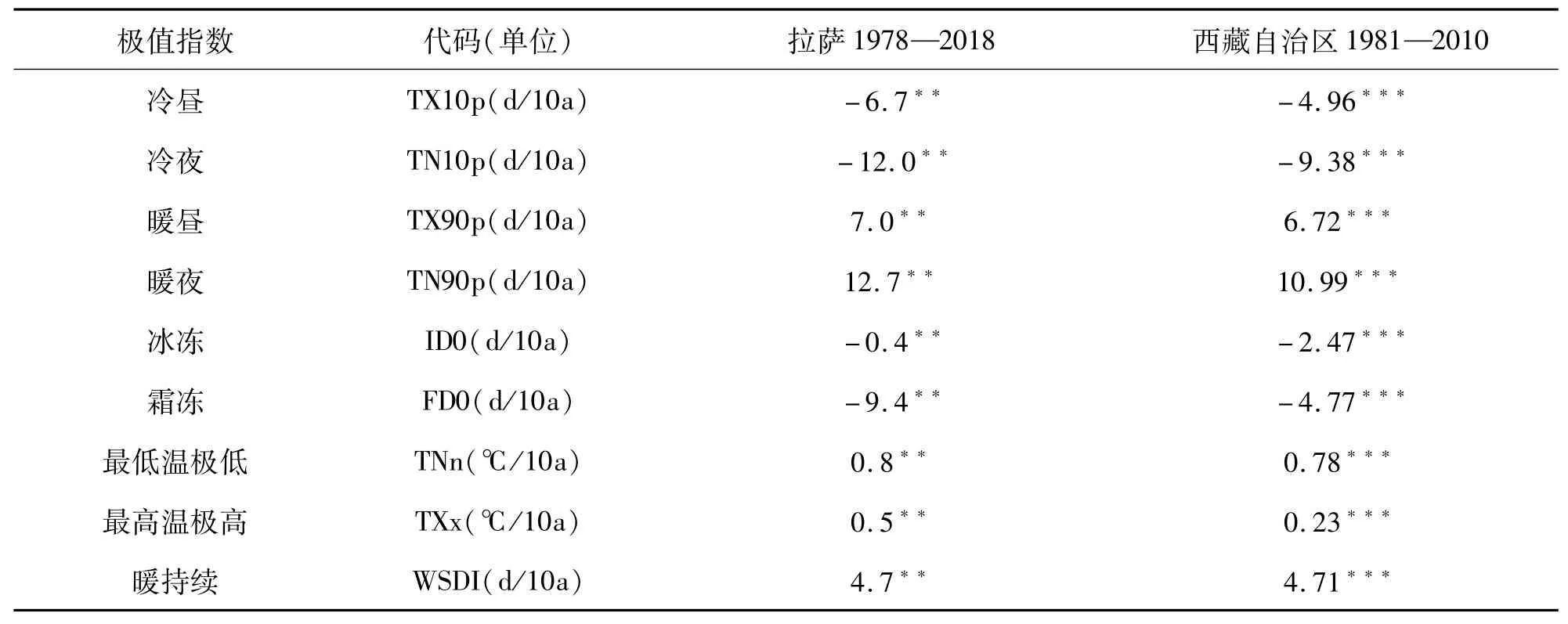
表2 拉萨极端气温指数变化趋势及其与西藏自治区的对比Tab.2 The trend of extreme temperature index in Lhasa and its comparison with Tibet autonomous region

将拉萨市极端气温指数线性趋势变化率的研究结果与杜军等［11］学者研究的西藏自治区极端气温指数的线性趋势变化率进行比较（见表2），发现其与西藏自治区极端气温指数的变化趋势基本一致，但是拉萨市极端气温指数的变化幅度（线性趋势变化率的绝对值）远大于西藏自治区极端气温指数的变化幅度，这也从侧面说明拉萨市的气温变暖趋势要显著于整个西藏自治区，对于造成这一差异的原因，主要是因为拉萨市是西藏自治区的省会城市，人口密度大，城市化进程加剧，受河谷地形和高原大气环流的影响，干旱而降雨量少，大风发生频率高［12］，轻、重工业比西藏其他地区相对发达，对环境造成的破坏也相对较大，影响了生态平衡，导致大气对环境的调节作用减弱.

通过对逐日最低气温进行分析处理，我们发现拉萨市近50年来的热夜日数（年内日最低气温大于20℃的天数）为0 d，这也符合拉萨市昼夜温差相差较大这一气候特点（日最低气温一般出现于晚上，且夜晚温度普遍较低），拉萨市地处高原，平均海拔3 650 m，空气稀薄，水汽、尘埃含量少，白天日照充足，太阳辐射强（稀薄的气体对其削减作用弱），地表吸热多、温度高，夜晚稀薄的气体对大地的保温作用弱，气温骤降，这也是拉萨市近50年来热夜日数为零的主要原因.

2.2 极端气温指数时序突变节点

运用Mann-Kendall非参数检验法，对拉萨市近50年来的日最高、日最低气温［图5（a′）和（b′）］和极端气温相对指数（图6）、绝对指数（图7）、极值指数（图8）、持续指数（图9）进行突变检验，并绘制出Mann-Kendall检测曲线图，检验统计量U的顺序、逆序变化曲线UBK和UFK的交点可能为突变点.由图5（a′）和（b′）可知极端最高气温趋势检测曲线在1994年出现交点，交点前后气温平均值分别为15.65℃、16.84℃，相差1.19℃，极端最低气温趋势检测曲线也在1995年出现交点，交点前后平均气温分别为1.26℃、3.24℃，相差1.98℃，但两者交点均在显著性水平α=0.05的两条临界线之外，表明极端最高、最低气温在时间序列上没有发生突变.

极端气温指数中暖（冷）夜日数在1996（1993）年出现交点，暖（冷）夜日数由偏少（多）期逐渐向偏多（少）期转变，霜冻日数在1995年出现交点，在交点之后呈现出递减趋势，日最低气温极低（高）值在1994（2000）年出现交点，日最高气温极低（高）值在1996（1991）年出现交点，极值气温均由相对偏冷期向相对偏暖期变化，但上述交点均在显著性水平α=0.05的临界线之外，表明以上极端气温指数在时间序列上均没有发生突变，而热夜日数TR20、冰冻日数ID0没有出现交点，因此也没有发生突变.

暖（冷）昼日数在1986（1987）年出现交点，暖（冷）昼日数由偏少（多）期向偏多（少）期转变，冷（暖）持续日数在1984（2002）年出现交点，冷（暖）持续日数减少（增多），夏季日数、生长季长度、气温日较差分别在1984、2001、1994年出现交点，且交点均在显著性水平α=0.05的临界线之内，表明以上极端气温指数在时间序列上均发生突变.

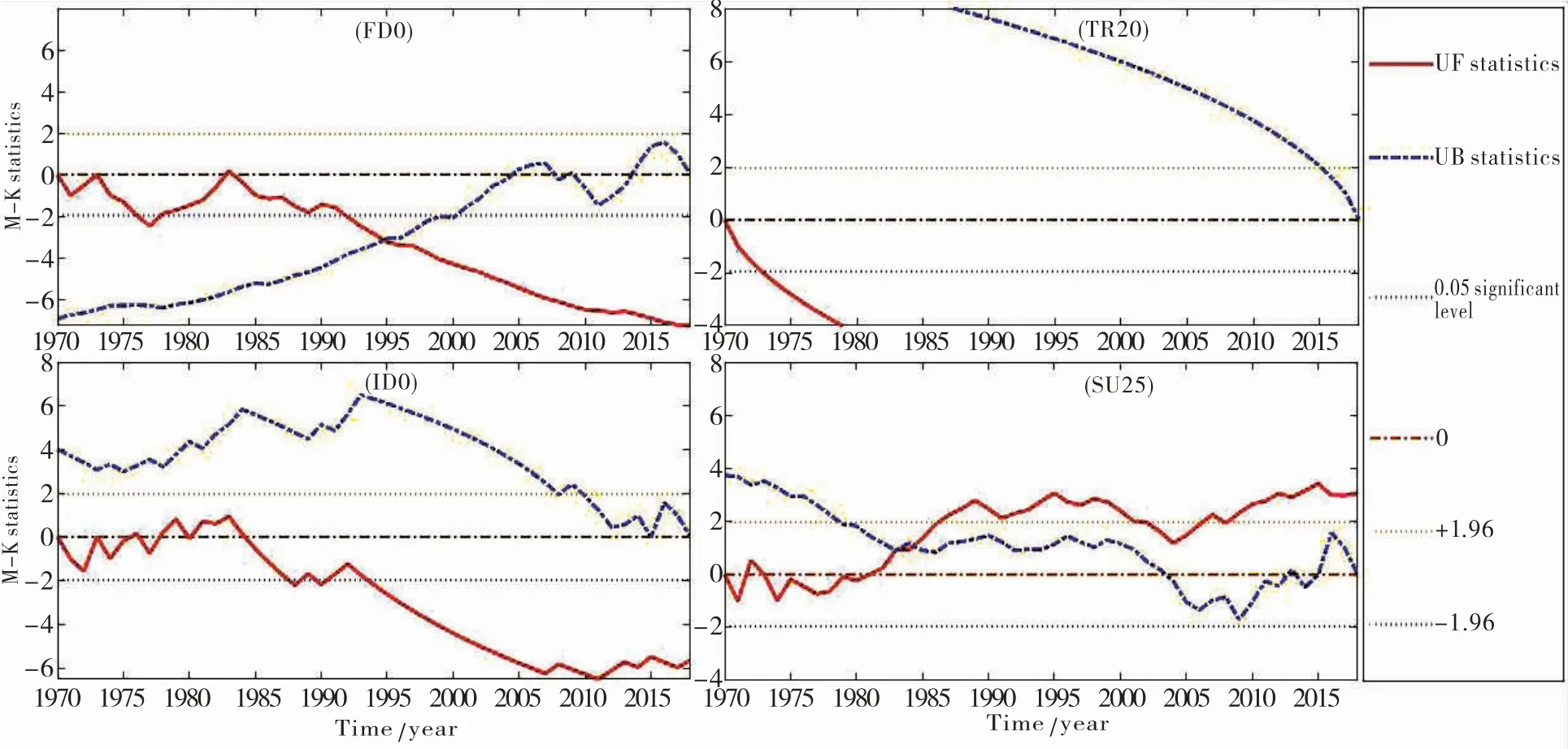
图7 拉萨市近50年极端气温绝对指数Mann-Kendall检测曲线图Fig.7 Absolute temperature index curve chart of extreme temperature by means of Mann-Kendall mutation test during the recent 50 years in Lhasa

2.3 极端最高、最低气温周期演变

运用Morlet小波对拉萨市年极端最高和最低气温数据进行周期演变分析，绘制了小波变换系数实部等值线图和小波方差图（图10）.小波实部等值线图反映出气温随着不同时间尺度冷暖交替变化情况，不同时间尺度对应的气温变化结构不同，许多小尺度的变化表现为镶嵌在较为复杂的较大尺度的结构当中.直观地显示出年平均气温的震荡周期变化特征较为复杂，实部图中颜色深浅和小波系数的大小来表示信号的强弱，正值说明气温偏暖；负值说明气温偏冷.年极端最高气温的小波系数实部等值线图显示出10年及以下的时间尺度，年极端最低气温变化周期较简单，突变点较少，波动极值点分布单一.10至20年尺度信号交替单一但震荡强度也较弱，说明气温在这一尺度多变但变化十分平缓；20至25年尺度的信号交替较为频繁震荡强度相对较强，说明气温在这一时间尺度上变化情况相对活跃；25至32年尺度信号交替频繁且强烈地震荡，说气温在此周期上出现明显的变化，故可初步推断其气温变化可能存在25至32年的周期.为了进一步明确主要周期，采用小波方差分析法，来分析气温随时间变化的主周期.由极端最高气温小波方差图可知，在28年出现明显的峰值，由此确定28年是拉萨年极端最高气温变化的主周期.

年极端最低气温的小波系数实部等值线图显示出3年及以下的时间尺度，年极端最低气温变化周期较简单，突变点较少，波动极值点分布单一.3至10年尺度信号交替非常频繁但震荡强度较弱，说明气温在这一尺度多变但变化比较平缓，可预测极端气温变化可能存在3到10年的周期.10至20年尺度的信号交替较为频繁震荡强度也较强，说明气温在这一时间尺度上变化情况相对活跃，初步推断其气温变化可能存在10至20年的周期.20至32年尺度信号交替频繁且强烈地震荡，说明气温在此周期上出现明显的变化，故可推断其气温变化可能存在25至32年的周期.为了进一步明确主要周期，采用小波方差分析法，来分析气温随时间变化的主周期.由极端最低气温小波方差图可知，在8、12、27年出现明显的峰值，由此确定8、12、27年是拉萨年极端最低气温变化的主周期.

图8 拉萨市近50年极端气温极值指数Mann-Kendall检测曲线图Fig.8 Extreme index curve chart of extreme temperature by means of Mann-Kendall mutation test during the recent 50 years in Lhasa

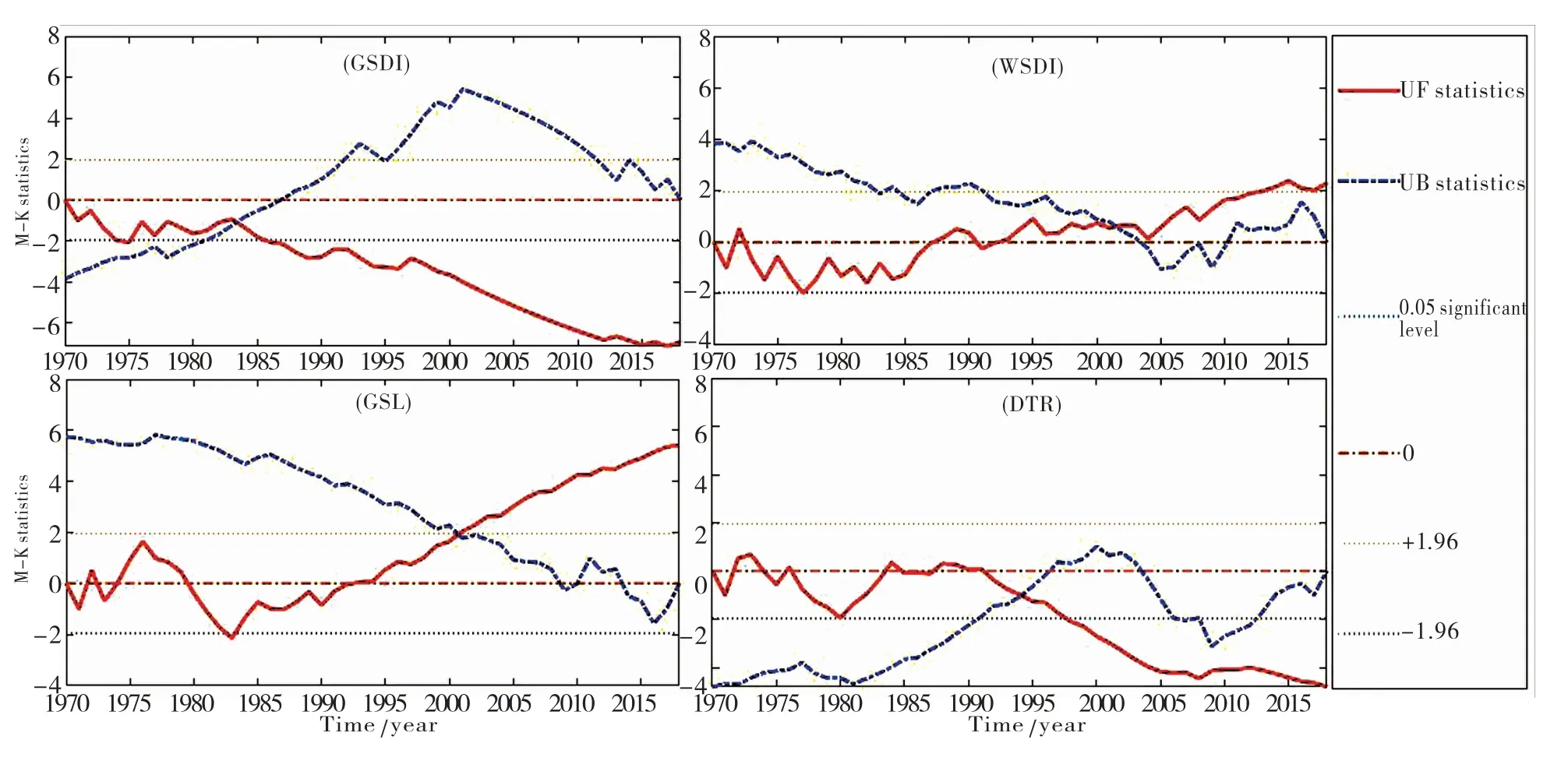
图9 拉萨市近50年极端气温持续指数Mann-Kendall检测曲线图Fig.9 Ongoing index curve chart of extreme temperature by means of Mann-Kendall mutation test during the recent 50 years in Lhasa

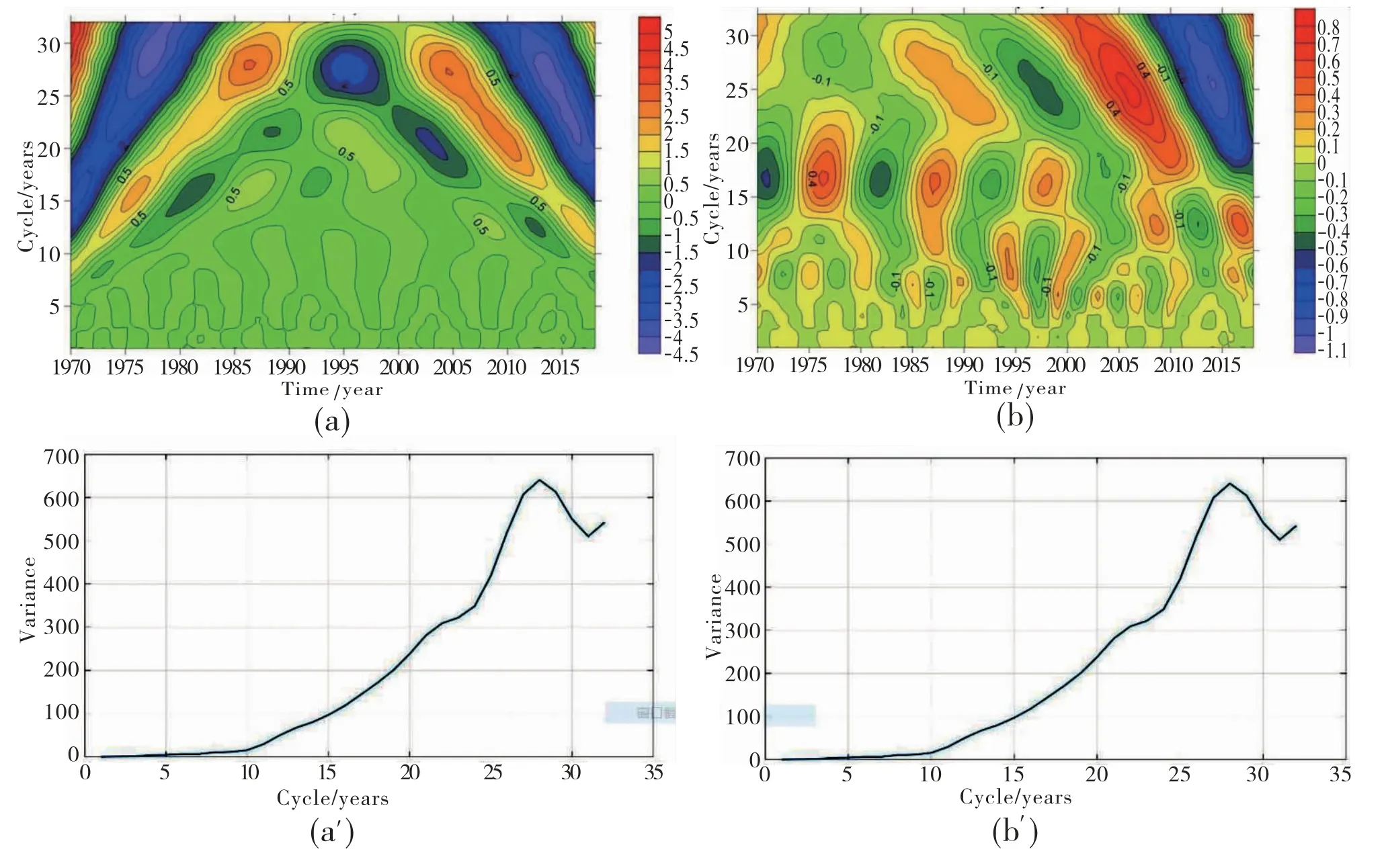
图10 拉萨市近50年日最低最高气温年平均小波分析图［（a）和（a′）：日最高年平均；（b）和（b′）：日最低年平均］Fig.10 Wavelet analysis chart of the annual mean minimum and maximum temperature during the recent 50 years in Lhasa［（a）and（a′）show the annual average value of daily maximum temperature，（b）and（b′）show the annual average value of daily minimum temperature］

3 结论与讨论

3.1 结论

本文基于拉萨市气象站点近50年来的逐日最高气温、最低气温、平均气温数据，采用一元线性回归分析、相关关系、Mann-Kendall非参数检验、Morlet小波分析等方法，分析了拉萨市极端最高、最低气温和极端气温指数在时间尺度上的年际变化趋势、突变节点、周期演变，最终得出了以下结论：

1）由回归分析可以看出，在10年际时间变化尺度上，极端最高、最低气温均呈现出波动上升趋势，升幅分别为0.48℃/10a、0.66℃/10a，其中极端最低气温上升的速率远大于极端最高气温上升的速率.极端温度偏高日数明显趋于增多，极端气温指数中的TX10p、TN10p、FD0、ID0、GSDI、DTR均呈现出下降趋势，TN90p、TX90p、SU25、TNn、TNx、TXn、TXx、WSDI、GSL均呈现出明显上升趋势.这与杜军研究的西藏自治区极端气温指数的变化趋势基本一致.但是，拉萨市极端气温的增幅要明显高于西藏地区，而且年平均气温变化与全球平均气温变暖趋势大体一致［13］，这也佐证了回归分析在研究极端气温变化过程中的可信性.

2）根据Mann-Kendall非参数检验可知，极端最高、最低气温趋势检测曲线分别在1994、1995年出现交点，且交点前后平均气温均相差1℃至2℃，但是交点都没有通过α=0.05的显著性检验，故极端最高、最低气温在时间尺度上没有发生突变.极端气温指数中的TN90p、TN10p、FD0、TNn、TNx、TXn、TXx虽然都在1991至2000年这一时间段内出现交点，但交点均在显著性水平α=0.05的临界线之外，所以以上极端气温指数在时间序列上均没有发生突变，而TR20、ID0没有出现交点，因此也没有发生突变.TX90p、TX10p、SU25、GSDI、WSDI、GSL、DTR均在1986至2002年这段时间内出现突变点，而且突变点前后极端气温指数的平均值相差甚大.这一研究结果与杜军、赵金鹏等［14］分别对西藏自治区和青藏高原极端气温变化的研究结果高度吻合，这也说明Mann-Kendall非参数检验法对于研究极端气温的突变情况有很大的适宜性，并且可信度极高.

3）小波实部等值线和小波方差图结果表明近50年来拉萨市年极端最低气温存在8、12、27年变化的主周期，拉萨年极端最高气温存在28年变化的主周期.

3.2 讨论

首先，利用多个极端气温指数，全面分析了拉萨市近50年来极端气温与其指数在时间尺度上的变化趋势，研究结果表明极端冷事件表现为下降趋势，极端暖事件表现为上升趋势，尽管还没有学者对拉萨市的极端气温变化进行系统研究，但是本文所研究的结果也基本符合青藏高原的气候变化特征［15-16］.

其次，根据拉萨市近50年来极端冷事件下降、极端暖事件上升的年际变化趋势，可以从侧面反映出拉萨市年平均气温逐渐升高这一事实，这也说明拉萨市在2019年6月出现高温，打破历史记录，也绝非偶然，甚至在未来，拉萨市年平均气温还可能会持续升高，不排除进一步刷新记录.

再次，影响拉萨地区极端气温和极端气温指数变化的原因甚多，不仅与特殊的地理位置有关，大尺度的大气环流对气温的变化也起着至关重要的作用.另外，地表覆盖面积的变化、CO2、CH4等一系列温室气体的排放都与气温变化有着紧密的联系［17］，其复杂的影响因素还需要更进一步的深入研究.希望将来掌握更多的气象要素，运用科学系统的分析方法，更好地探究拉萨地区气温变化的趋势和原因，同时也希望为研究青藏高原的气候变化提供一定的帮助.

致谢：感谢AliCPT项目组成员单位、阿里地区气象局等兄弟单位的大力支持.