求解约束优化问题的元胞混洗蛙跳算法及应用

张 强, 姜慧清, 王 颖, 郭玉洁

(东北石油大学 计算机与信息技术学院, 黑龙江 大庆 163318)

0 引 言

混洗蛙跳算法[1](SFLA: Shuffled Frog Leaping Algorithm)在求解优化问题时具有以下优势： 1) 采用多族群的种群结构, 使其能很好地求解具有不连续的、 非凸的、 存在局部最优等特点的复杂目标函数, 且易实现并行计算； 2) 采用多子群全局寻优和局部寻优相结合的模因进化机制, 使算法拥有较好的全局寻优能力和快速收敛效率, 已被应用于函数优化[2-3]、 车间调度[4]、 故障诊断[5]、 聚类问题[6]和图像处理[7]等多个领域。但SFLA在解决多模优化问题时也存在寻优精度低、 易于陷入局部最优的问题。许多学者在族群多样化[8-9]、 进化方式改进[10-13]和算法融合[14-15]等方面做了一些研究。分析其原因主要是由混洗蛙跳算法的分组方法与进化方式引起的。SFLA的分组是通过适应值降序排序后进行分组, 导致最后一个子群的青蛙都不如之前子群中的青蛙, 而SFLA的进化方式是先参照子群内最优青蛙, 再参照族群内最优青蛙, 这样最后子群的青蛙可能需要较多的进化计算, 并且最差青蛙进化公式中没有有效借鉴族群内其他青蛙的进化信息, 导致子群易于被限制在较小的寻优空间。元胞自动机[16](CA: Cellular Automata)是依据一定演化规则在离散时间维上同步演化的动力学系统, 能通过简单的局部转换规则模拟全局演化的复杂情况, 已广泛应用于社会、 经济和科学研究的相关领域[17-18]。目前元胞自动机理论与智能进化算法相结合方面的研究主要有元胞遗传算法[19]、 元胞微粒群算法[20]、 元胞蝙蝠算法[21]和元胞差分进化算法[22]等。Elbeltagi等[23]通过研究得知SFLA在求解一些离散和连续优化问题的成功率和寻优速度优于遗传算法、 模因算法和蚁群算法。笔者提出基于元胞自动机的改进混洗蛙跳算法(CA_SFLA: improved Shuffled Frog Leaping Algorithm based on Cellular Automata), 该算法利用元胞自动机的邻域结构和演化规则保持青蛙族群内个体的多样性, 利用改进的进化方式和混沌变异方式进化青蛙个体的3种状态, 进而平衡局部搜索和全局寻优的关系, 提高算法在搜索空间的寻优速度和精度。

1 基本混洗蛙跳算法

1.1 种群初始化

混洗蛙跳算法将每只青蛙看作待优化问题的一个解, 设定青蛙族群规模为P(P=mn), 其中m为子群个数,n为子群内青蛙个数, 最大进化代数T, 子群内部进化次数为t。

1.2 子群划分

计算每个青蛙的适应度f(X), 并按降序排序, 依据

Gk={X(j)k,f(j)k|X(j)k=

X(k+m(j-1)),f(j)k=f(k+m(j-1))}

(1)

将青蛙族群分成m个子群Gk, 每个子群内共有n个青蛙, 具体分组示意如图1所示。设定蛙群中适应值最好的青蛙为Pg, 其中X(j)k为第k个分组里第j个青蛙,j=1,2,…,n;k=1,2,…,m。

图1 蛙跳算法分组示意图Fig.1 Schematic diagram of leapfrog algorithm grouping

1.3 子群内青蛙进化

设定每个子群内最优解为Xb, 最差解为Xw, 利用

(2)

(3)

1.4 种群信息共享及算法终止条件

每个子群分别迭代指定次数后, 如果达到群体进化最大进化代数T或是满足寻优精度, 则输出结果; 否则将所有青蛙个体整合完成青蛙种群的信息共享, 继续执行子群划分、 子群个体进化直到满足算法终止条件。

2 元胞混洗蛙跳算法原理

2.1 元胞自动机的构成

在元胞混洗蛙跳算法中, 每个青蛙作为一个独立的元胞被放在元胞自动机的网格里。此时元胞混洗蛙跳算法可以由4元组A={Ld,S,N,f}定义, 其中元素定义如下。

1)Ld表示元胞空间。从理论上讲元胞空间的维数是任意的, 但随着维数的增加空间结构复杂度则越大, 在实际应用中常用的是二维元胞自动机(d=2)。

2)S表示元胞的状态。考虑到青蛙个体存在冬眠的生理现象, 笔者算法设定青蛙个体的元胞状态有生、 休眠和死3种状态, 分别用0、1、2表示, 在算法运行时进行初始化。

3)N表示元胞的邻域。常用的邻域模型有冯·诺依曼型、 摩尔型和扩展摩尔型(见图2)。笔者选用摩尔型邻域模型, 即每个元胞周围有8个元胞青蛙个体。

a 冯·诺依曼型 b 摩尔型 c 扩展摩尔型

2.2 元胞混洗蛙跳算法原理

2.2.1 个体状态演化规则

笔者算法利用元胞的邻域结构代替基本蛙跳算法的分组方法, 进而克服经典混洗蛙跳算法分组的缺点。文献[13]利用中心元胞邻域内个体的数量确定其状态, 而在求解具体应用问题时则需要根据优化问题的特征构建元胞个体的演化规则, 否则会由于不适合的演化规则而引发生命危机。设每个元胞具有“生”、 “休眠”和“死”3种状态。定义如下。

1) “生”状态。如果该中心元胞青蛙个体满足所有约束条件或邻域周围有满足约束条件的青蛙个体, 则状态设置为“生”状态。

2) “休眠”状态。如果该元胞青蛙个体不是邻域所有元胞中的最差青蛙, 本身不满足约束条件, 周围也没有满足约束条件的个体, 则状态设置为“休眠”状态, 当周围有满足约束条件的元胞青蛙时被复活为“生”状态。

3) “死”状态。如果该元胞青蛙是邻域所有元胞中最差的青蛙, 且不满足优化问题的约束条件, 周围也没有满足约束条件的青蛙个体, 则置为“死”状态。

算法运行初始时根据元胞青蛙个体的适应值设置相应的状态, 此时不考虑优化问题的约束条件。具体初始化方式如下： 1) 计算所有元胞青蛙个体的适应值平均值, 设置元胞青蛙个体适应值超过平均值的青蛙个体状态为“生”状态； 2)青蛙个体适应值小于平均值的个体设置前一半个体的状态为“休眠”状态, 剩下的个体设置为“死”状态。

2.2.2 个体进化方式改进

经典蛙跳算法子群最差个体在进化过程中没有有效借鉴族群内其他青蛙的进化信息, 导致算法在求解多维复杂优化问题时容易落入局部最优解。笔者所提元胞混洗蛙跳算法每次更新的是状态为“生”或是“死”的元胞青蛙, 将该元胞青蛙与其邻域内的元胞青蛙构成元胞混洗蛙跳算法的子种群, 这样该元胞会出现以下3种更新状态。

1) 状态1。该元胞的状态为“活”, 且该元胞是该子群的最优值且满足所有约束条件, 依据SFLA的进化方式是不需要更新的, 但社会学原理研究表明, 优秀个体的附近更易找到更优个体, 即局部最优青蛙个体附近有可能存在更优的青蛙个体。笔者借鉴鲸鱼算法通过模拟座头鲸在一个缩小的圆圈内绕着猎物游动, 同时沿着螺旋形的路径游动的捕食行为获取局部最优个体周围的更优个体, 按照

(4)

计算生成个体的适应值, 如果优于当前个体则替换。其中Xg(t)为全局最优青蛙所在的位置,D′=|Xg(t)-X(t)|,A=2α·r-α,p为[0,1]随机概率,l为[-1,1]随机概率。α在迭代过程中从2～0线性递减；r为[0,1]随机数组成的向量。

2) 状态2。该元胞的状态为“活”, 但本身不满足约束条件, 则可以根据邻域的满足约束条件的个体进行更新。首先选择中心元胞邻域内满足约束条件且适应值最小的青蛙个体作为子群里局部最优解Xb(t), 按照式(2)更新当前中心元胞个体的位置, 如果适应值有改善且满足约束条件, 则替换当前个体; 否则采用

(5)

更新个体。其中Xg(t)为族群最优青蛙所在的位置。

3) 状态3。该元胞的状态为“死”, 应用k阶Chebyshev混沌映射对个体进行映射, 如下

X(t+1)=cos(karccosX(t)),k≥2

(6)

其中k为偶数时产生的混沌映射序列随机性更好, 生成的青蛙个体新位置呈现遍历性和多样性, 可有效地在收敛区域以外空间搜索全局最优位置。

2.3 元胞混洗蛙跳算法流程

元胞混洗蛙跳算法流程如图3所示。

图3 元胞混洗蛙跳算法流程图Fig.3 Flowchart of cellular shuffled frog leaping algorithm

3 实验仿真

3.1 函数极值优化

为了深入研究SFLA_CA算法的性能(约束条件设置为元胞个体的适应值优于元胞邻域内所有个体的适应度平均值), 将其与SFLA[1]、 MSFLA(Modified Shuffled Frog Leaping Algorition)[10]、 MSFLA1[11]、 ISFLA[12]和MSFLA2[13]进行了比较。10个测试函数包括单峰问题和多峰问题。所有实验均在Intel(R)Core(TM)i7 8750H CPU双核处理器2.20 GHz和2.21 GHz上实现, 具有16 GByte内存物理地址扩展。所有算法均在Microsoft Windows 10 Professional环境下用MATLAB R2014a进行编码和实现。各算法的参数设置如下： SFLA_CA、 SFLA、 MSFLA、 MSFLA1、 MSFLA2和ISFLA的种群个数均设置为P=64, 分组个数为8, 子群内个体数为8, 每个算法分别计算20次取平均值。测试函数如表1所示, 每种算法分别对10个函数的500维进行优化对比, 性能对比结果如表2所示。

表1 10个典型优化函数

从表2可以看出, 对单峰函数F1-F3所提算法的寻优性能效果明显优于其他对比算法。对多峰函数F6和F8, 即使是500维优化也能找到全局最优解。对函数F4、F5和F7, SFLA_CA与MSFLA2的寻优效果相似, 但SFLA_CA的平均值和标准差要好一些。对F9和F10, SFLA_CA与其他改进算法相比, 寻优效果要好几个数量级。分析其原因： 1) 利用元胞自动机的邻域结构和演化规则可以降低算法的选择压力, 有利于保持寻优过程中青蛙种群的多样性, 增加迭代过程中寻找到更优个体的几率, 有利于避免算法陷入局部最优解； 2) 对“生”的个体利用螺旋方式在最优个体周围查找更优解加速了算法的收敛速度和计算精度； 3) 对“休眠”的个体在进化过程中借鉴了周围邻域的个体, 较好地平衡了个体进行局部寻优和全局探索； 4) 对“死”的个体则采用混沌策略增加了种群个体的多样性。

表2 500维函数优化性能对比

3.2 油田措施规划方案优化

实际油田生产过程中, 有些措施的有效期可能会影响下一年的产量, 即当年的投入效益会延续到下一年, 所以有必要对近几年的措施工作进行统一安排, 做到产出投入经济效益最大化。笔者以措施规划年(文中规划期为3年)的产出投入比f(X,Y)最大化为优化目标, 以每年的规划增油量、 增液量和增注量等为约束条件, 并考虑措施和受效增油递减率, 可得到模型的具体形式如下

其中N为井数目,L为措施数,M为措施年数,k为年份,Xij为第i口油井实施措施数j,Yij为第i口水井实施措施数j,aij为第i口井实施措施j的初始日增油,bij为第i口井实施措施j的初始日增注,cij为第i口井实施措施j的初始日增液,tij为第i口井实施措施j的有效天数,dij为第i口井实施措施j的本年有效天数,gij为第i口油井实施措施数j的递减率,hij为第i口水井实施措施数j的递减率,ck为第k年的油价,ek为第k年的吨油成本、rk为第k年的吨水费用、uk为第k年的吨液费用,pijk为在第k年的第i口井实施措施j的单价,H是油井年度增油目标,J是水井年度增油目标,Q为年度增液目标,R为年度增注目标,α为误差百分比,Lij为油井或水井的措施上限数,Mij为第i口井实施措施数j的月份, [S,E]为实施措施月份的区间,vk-1为规划前一年的措施对当年增油量的影响,qk-1为规划前一年的措施对当年增注量的影响,zk-1为规划前一年的措施对当年增液量的影响, 计算方法即第k-1年实施某项措施的有效期dij减去第k-1年措施有效天数tij, 再乘以每天的增油量或是增液量或是增注量。

结合某采油厂3年的措施规划工作, 可规划的措施油水井共用3 283口, 每年所采取的措施及工作量上限及施工安排的月份如表3所示, 应用SFLA_CA、 SFLA、 MSFLA、 MSFLA1、 ISFLA和MSFLA2求解油田措施模型, 算法的参数设置如同3.1节, 实验结果如表4所示。

表3 措施上限及实施月份

从表4的实验对比结果可知, 对于最优值、 最差值和平均值, 笔者所提的SFLA_CA优化结果最好。主要原因是该优化问题的编码方式是将3283口井及措施的月份作为变量, 所以需要优化的维数较高, 而笔者算法在求解高维问题时具有较快的收敛速度和寻优精度。

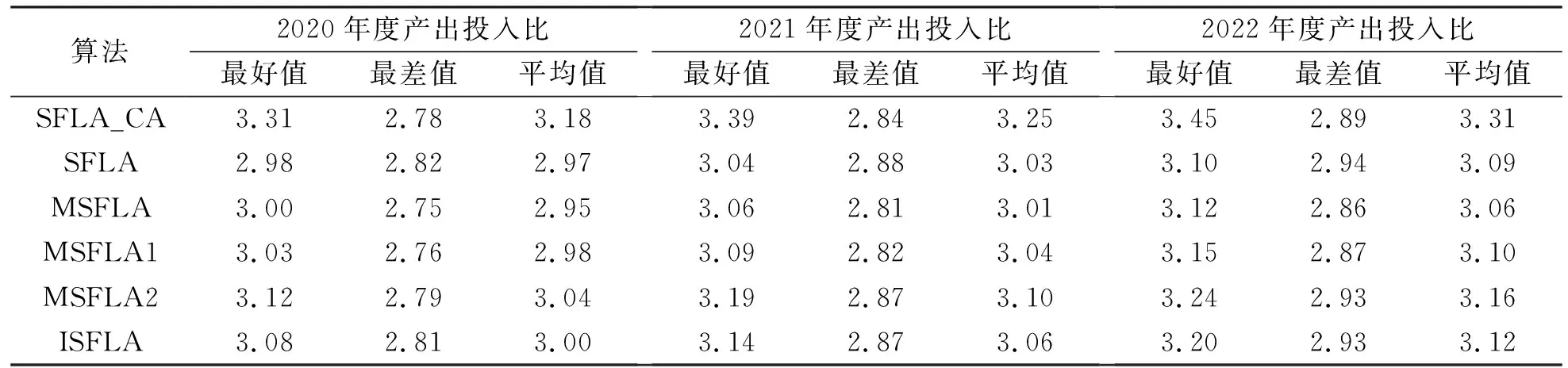
表4 6种算法年度产出投入比结果对比

4 结 语

笔者基于元胞自动机的优势提出一种求解约束优化问题的元胞混洗蛙跳算法, 通过对3种不同状态的个体实施不同的进化规则加速寻优性能, 并通过个体状态演化规则完成个体状态的转变, 降低了算法的选择压力, 保证了寻优过程中蛙群的多样性。通过经典基准函数测试和油田措施规划方案优化效果对比, 可知笔者算法对求解高维优化问题具有很好的适应性。