改进的PSO-VMD算法及其在管道泄漏检测中的应用
张 超, 侯 男, 路敬祎, 王 闯
(东北石油大学 a. 人工智能能源研究院; b. 黑龙江省网络化与智能控制重点实验室, 黑龙江 大庆 163318)
0 引 言
管道运输作为能源存储与使用的常用手段, 具有运输成本低、 适用性强等优势, 但管道存在设备老化以及人为破坏等多种外部因素, 管道泄漏时有发生, 甚至对人们的生命财产安全造成伤害[1]。为了避免或降低管道泄漏事故的发生, 对管道泄漏检测技术的研究非常必要。目前常用的去噪方法主要有傅里叶变换、 小波变换等, 但这些方法不能依据信号自身的特点自行确定对应的分解条件, 在先验经验的影响下会产生误差而导致精度下降。Huang等[2]提出了一种称为经验模态分解(EMD: Empirical Mode Decomposition)的自适应信号处理技术, 该方法能较好地处理非线性和非平稳信号。但是, EMD存在端点效应和模态混叠的弊端, 使信号分解效果不理想。Smith[3]在经验模态分解方法的基础上提出了一种新型自适应的时频分析方法----局域均值分解(LMD: Local Mean Decomposition)。LMD虽然可以对信号进行滤波, 但是解调过程会导致信号出现突变。
Dragomiretskiy等[4]提出VMD(Variational Mode Decomposition)算法, 是一种自适应信号处理方法, 可有效克服EMD算法的端点效应和模态混叠问题。预设尺度k和惩罚因子α对分解效果有很大的影响, 而人为经验设定的k过大或过小通常会导致过分解或欠分解现象;α越大模态分量带宽越小; 反之,α越小模态分量的带宽就越大。由此可知VMD参数的设置决定是否能准确提取出信号的有用信息。为减少人为设置参数可能导致的不良影响, 蒋丽英等[5]采用粒子群优化算法对VMD算法的最佳影响参数组合[k,α]进行搜索, 利用参数优化后的VMD算法分解采集的齿轮数据, 并应用到齿轮故障特征参数提取。
笔者采用粒子群优化算法对VMD参数组进行寻优处理, 而粒子群算法在后期容易收敛缓慢, 陷入局部最优, 无法得到较为准确的结果。针对上述问题, 笔者提出了一种利用混沌算法、 Sigmoid函数改进PSO(Particle Swarm Optimization)优化VMD的改进算法, 能得到k和α的最优解, 然后利用VMD对仿真信号进行分解, 分别计算仿真信号的概率密度函数(PDF: Probability Density Function)和每个模态分量的PDF之间的欧氏距离, 根据相似性大小选择主要模态分量进行重构, 从而消除噪声的干扰。通过算法仿真和管道数据实验分析, 结果表明改进的PSO-VMD算法具有较好的去噪性能, 并验证了该方法在管道泄漏检测中应用的可行性。
1 变分模态分解基本原理
VMD算法将输入的信号进行模态分离处理后, 每个IMF(Intrinsic Mode Function)分量的带宽和频率中心由连续迭代确定, 由k个IMF分量组成集合uk={u1,u2,…,uk},k=1,2,…,k, 获得的每个IMF分量具体步骤如下:
1) 利用希尔伯特变换, 计算每个uk的解析函数, 得到与其对应的边际谱;
2) 通过指数混合调制到估计的中心频率, 将每个模态uk的频谱转移到对应的基带;
3) 由解调信号的高斯光滑度和梯度平方准则方法估计带宽大小。
上述步骤获得的约束变分问题为

(1)

(2)
其中*为卷积;f为分解的主信号;ωk={ω1,ω2,…,ωk}为其各自对应的中心频率; ∂t为对函数求时间的导数;δ(t)为单位脉冲函数。
在求解约束问题时, 需要考虑惩罚因子α和用λ(T)表示的拉格朗日乘子这两项。将引入的两项结合得到扩展的拉格朗日表达式如下
通常采用乘法算子交替方向解决上述问题, 对uk+1,ωk+1,λk+1不断迭代优化求取扩展拉格朗日表达式的“鞍点”。
对信号进行VMD分解的具体步骤如下:
2) 执行循环, 令n=n+1, 更新uk和ωk

(4)

(5)
3) 更新乘法算子λ
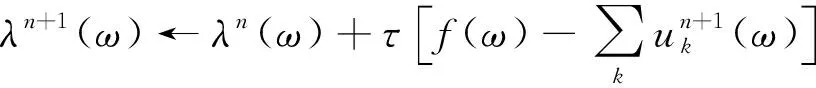
(6)
2 粒子群优化算法
粒子群优化算法是在人类对鸟类捕食行为研究的基础上得到的一种进化计算方法[6]。粒子群优化算法作为一种启发式智能算法, 整个群体由d维搜索空间中移动的N个粒子组成[7], 第i个粒子在空间中的位置表示为Xid=(Xi1,Xi2,…,Xid), 第i个粒子历史最优位置表示为Pid=(Pi1,Pi2,…,Pid), 全部粒子群历史最优位置表示为Gid=(Gi1,Gi2,…,Gid), 第i个粒子的历史速度表示为Vid=(Vi1,Vi2,…,Vid)。
在每次迭代过程中, 粒子通过个体极值和群体极值更新自身的速度和位置, 更新公式如下
Vid(t+1)=ωVid(t)+c1r1(Pid(t)-Xid(t))+c2r2(Gid(t)-Xid(t))
(7)
Xid(t+1)=Xid(t)+Vid(t+1)
(8)
其中ω为惯性系数,c1和c2为加速系数, 代表认知系数和社会系数。r1和r2为[0,1]之间服从均匀分布的两个独立随机数。由式(7)和式(8)可以看到, 参数ω、c1、c2的取值对粒子的更新速度和位置有很大的影响。文献[8]表明当惯性权值较大时, 粒子搜索能力增强, 局部细调能力减弱; 反之, 当惯性权值较小时,粒子的局部开发能力增强, 探测能力减弱。适当调整加速因子不仅便于粒子实现快速搜索, 提高全局搜索能力, 同时利于局部的精细化, 获得更好的全局最优解[9]。由此可见, 选取恰当的参数是研究和改进粒子群优化算法性能的关键。
3 改进的PSO算法
3.1 混沌算法
混沌是一种看似比较凌乱, 但实际却是非常有规则的运动[10], 具有遍历性、 随机性和规律性等特性。混沌算法的主要思想是先将种群进行混沌优化, 再将其映射到原解所在的空间范围内。混沌优化后使结果跳出局部最优, 并且收敛速度加快。笔者主要使用混沌算法对粒子群的加速因子进行初始优化, 使其跳出局部最优, 加快寻优。混沌有很多动力学模型, 笔者采用一维非线性映射模型Logistic映射[11]
Y(t+1)=μY(t)(1-Y(t))
(9)
其中Y(t)是自变量,μ是控制变量, 当μ=4时, 系统处于完全混沌状态, 式(9)产生的序列为混沌变量。
3.2 Sigmoid函数
Sigmoid函数常被用于神经网络的激活函数, 将变量映射到(0,1)之间

(10)
Sigmoid函数拥有平滑的上下边界域, 当x<-9.903 438时,f(x)=0; 当x≥9.903 438时,f(x)=1。
3.3 优化PSO参数
对粒子群中的加速因子进行混沌优化, 映射到原解空间为
c1s=(0.5-0.9)(i-j)/i+0.9
(11)
其中i=20为最大迭代次数,j为当前迭代次数,c1s为加速因子终值。
式(11)是在区间[0.5,0.9]上变化的单调递增函数, 代入到混沌映射模型式(9)中变成一个在[1,0.36]上的递减函数, 经过反复仿真实验可知, 式(11)代入混沌映射模型后乘上常数θ=2得到
c1=4.0θc1s(1-c1s)
(12)
其中常数θ=2, 使c1数值由2递减至0.72时, 算法可以获得最优的适应度值
c2s=(0.9-0.5)(i-j)/i+0.5
(13)
c2=4.0θc2s(1-c2s)
(14)
其中c2s为加速因子终值,c2原理同c1。这样的改进可使粒子在迭代初期,c1值较大,c2值较小, 有利于粒子增强全局搜索能力; 随着迭代次数的增加,c1值变得较小,c2值变得较大, 这样有利于局部的细节化, 使粒子局部搜索能力增强。因为在收敛后期个体极值影响变小, 全局极值影响加大, 所以这两个函数能更加细化这一影响。
采用Sigmoid函数优化惯性权重, 即

(15)
由式(15)可见, 在迭代初期,ω值为1, 随着迭代次数的不断增加,ω逐渐减小, 最后减小到0.5。当惯性权值较大时, 粒子全局搜索能力增强; 迭代后期, 惯性权值较小时, 粒子的速度不断减小, 局部开发能力增强, 有利于粒子局部搜索的精细化。
4 改进的PSO-VMD-ED算法
VMD对信号进行分解前, 需要人为经验设定预设尺度k和惩罚因子α, 而参数组合[k,α]对信号分解效果有很大的影响。通过对上述算法的研究, 笔者采用混沌算法和Sigmoid函数改进PSO算法, 再利用改进的PSO优化VMD参数, 而PSO在对VMD参数进行寻优搜索时需要确定一个适应度函数, 粒子通过与新粒子适应度值作比较以更新粒子位置, 笔者选取包络熵作为适应度函数。零均值信号f(j)(j=1,2,…,N)的包络熵EP如下

(16)
其中Pj为a(j)的归一化形式;a(j)为信号f(j)经Hilbert解调后得到的包络信号。包络熵反应了信号的稀疏程度, 如果得到的IMF分量所含噪声越多, 则信号的稀疏程度越小, 包络熵值就越大; 如果IMF分量的噪声越少, 规律性越强, 则信号的稀疏程度越大, 包络熵值也就越小。包络熵值最小的一个分量为含有故障特征信息的最佳分量。
当第i个粒子处于某一位置Xid时, 计算此位置条件下VMD处理得到的所有IMF分量的包络熵值, 将最小包络熵值称为局部极小熵值minEP。改进的PSO-VMD算法流程图如图1所示。

图1 改进PSO优化VMD算法流程图Fig.1 Flow chart of improved PSO optimization VMD algorithm
改进的PSO-VMD算法基本步骤如下:
1) 初始化粒子群;
2) 令个体极值和全局极值为粒子初始位置;
3) 更新惯性权重、 加速因子以及速度模型;
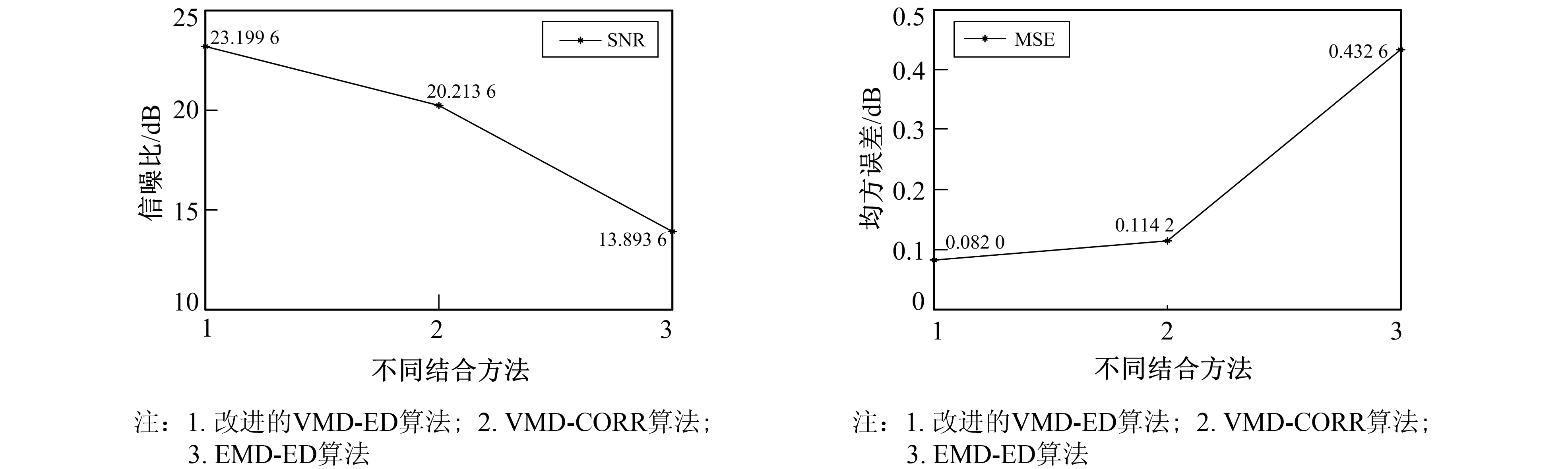
4) 在不同粒子位置下对信号作VMD处理, 计算每个粒子的适应度值minEP, 比较适应度值大小, 求出个体极值Pbestd, 若y(Pid) 5) 计算全局极值Gbestd, 若y(Pbestd) 6) 判断是否达到了设定的最大迭代次数, 若满足则输出全局最优位置及适应度值, 算法结束; 否则, 跳转到步骤3)。 信号滤波即降噪, 主要利用有用信号和噪声信号在时频域分布的不同特性进行筛选并剔除背景噪声信号, 达到增强有用信号的目的。振荡幅度是信号的一个重要特性, 而概率密度函数包含了信号分解模态的完整特征信息。因此, 需计算原始信号与每个模态的PDF, 通过相似性测量方法评估分解模态与原始信号的PDF之间的相似性, 故选用欧氏距离的几何测量方法。 欧氏距离是易于理解的一种计算距离的方法, 指在M维空间中两个点之间的真实距离, 或向量的自然长度。在二维和三维空间中的欧氏距离就是两点之间的实际距离。M维空间中A点与B点之间的欧氏距离可表示为 (17) 其中A点坐标为(a1,a2,…,an),B点坐标为(b1,b2,…,bn)。 利用各模态分量与原始信号的概率密度函数之间的欧氏距离表示其与原始信号的相似程度L, 如下 L(i)=D[P(x(t)),P(Hi(t))] (18) 其中P为概率密度函数(PDF),H为本征模态函数(BLIMF: Band-Limited Intrinsic Mode Function)。 当坡度显著增加时, 表明在该BLIMF之后发生的相似性迅速降低。将θ定义为相邻两个BLIMF之间的最大斜率 θ=max|L(i)-L(i+1)|,i=1,2,…,(N-1) (19) 通过比较仿真信号与VMD各模态分量的PDF之间的欧氏距离, 以ED增量最大的两个相邻模态分量作为有效分量选取的转折点, 将ED突变最大及其之后的模态分量都视为噪声信号。这样的选取方法可以筛选出真正的有效模态, 达到去噪的效果。 为了验证改进算法的有效性, 选取含各分量为5 Hz,50 Hz,200 Hz 3个频段的余弦信号作为原始信号并加入噪声强度为20 dB的高斯白噪声进行仿真分析, 仿真信号为 f(x)=1.2cos(10πt)+cos(100πt)+0.6cos(400πt)+λ (20) 原始仿真信号如图2a所示, 其中, 由改进的PSO-VMD算法得到的最优解带宽参数α=4 000, 预设尺度k=5, 信号采样频率为1 000 Hz, 对该信号进行分解, 经VMD分解后得到的5个模态分量结果如图2b~图2f所示。VMD分解后得到的5个IMF分量的频谱曲线如图3所示。 图2 原始复合信号和VMD分解得到的5个模态Fig.2 Five modes obtained from the original composite signal and VMD decomposition 由图3可知, VMD算法具有很强的中心频率捕获能力, 从式(20)可知, 该复合信号的中心频率分别为5·2π Hz, 50·2π Hz, 200·2π Hz, 对应图3中前3个模态分量的频谱曲线图的峰值: 5·2π、 50·2π、 200·2π。 图3 VMD分解得到的5个IMF分量的频谱曲线Fig.3 Spectrum curves of five IMF components obtained by VMD decomposition 加噪后的仿真信号经VMD分解, 得到了5个模态分量, 分别计算加噪后的仿真信号和5个模态分量的幅值概率密度函数, 如图4所示。 由图4可以看出, 不同模态分量的概率密度函数差别很大, 为了进一步比较各个成分间的差别, 分别计算VMD各个模态分量的PDF和加噪后仿真信号的PDF之间的欧氏距离, 如图5所示。 图4 加噪仿真信号和VMD模态分量的概率密度函数Fig.4 Probability density functions of the noisy simulation signal and VMD modal components 由图5可以看出, 前3个模态分量的欧氏距离明显小于其他分量, 这与仿真信号的构成相符合。根据式(17)~式(19)选取增量最大的两个相邻模态分量作为有效分量选取的转折点, 因此, 选择前3个有效模态对信号进行重构。类似地, 采用文献[12]中提出的基于VMD与相关系数的去噪方法(VMD-CORR: Variational Mode Decomposition-Correlation Coeffificient), 将EMD自适应分解后得到的k作为VMD的参数, 输入人为经验设定α值, 设置阈值为0.3, 选取相关系数大于0.3的有效分量进行重构, 对加噪后的信号进行去噪。采用Komaty等[13]提出的基于EMD与欧氏距离的去噪方法(EMD-ED), 对仿真信号先进行EMD分解, 再与欧氏距离结合, 选取有效模态进行重构。为全面地评估以上方法的性能, 笔者分别计算以上方法重构信号的信噪比(SNR: Signal Noise Ratio)和均方误差(MSE: Mean Square Error), 结果对比如图6、 图7所示。 图5 VMD各模态分量的PDF的欧氏距离Fig.5 Euclidean distance of PDF for each modal component of VMD 信噪比又称讯噪比, 指系统中信号与噪声的比例, 定义为 (21) 其中PS和PN分别为信号和噪声的有效功率。当SSNR=0, 此时信号平均功率与噪声平均功率相等, 信号可靠性极低; 当SSNR<0, 此时噪声超过信号功率的1/10, 即信号已淹没在噪声中。 (22) 从图6可以看出, VMD-CORR算法和EMD-ED算法对信号去噪后的信噪比分别为20.213 6 dB、 13.893 6 dB, 而笔者提出的改进VMD算法可以提高信号的信噪比, 达到23.199 6 dB。从图7可以看出, VMD-CORR算法和EMD-ED算法对信号去噪后的均方误差分别为0.114 2 dB、0.432 6 dB, 笔者改进的VMD算法的均方误差则最小, 为0.082 0 dB。故改进后的算法能有效去除信号中的噪声, 去噪效果优于未改进的VMD-CORR算法以及EMD-ED算法, 得到了较为理想的去噪效果。 图6 SSNR对比图 Fig.6 SSNR contrast diagram 为了验证笔者算法的有效性, 将此算法应用到实际管道上, 并与VMD-CORR算法以及EMD-ED算法做对比实验。笔者的实验数据采用天然气管道泄漏检测模拟实验平台, 该实验平台的管道长160 m, 管径为DN50, 管壁厚1 cm, 管道上设置了多个泄漏点, 各泄漏点间距为10 m, 由4分球阀连接。其中气体压力为0.5 MPa, 流量60 m3/h。检测实验平台如图8所示。笔者采用Labview编程环境对数据采集, 用于收集管道数据的采集卡是NI-9215采集卡, 采样频率为3 kHz。通过迅速切换球阀开关模拟管道泄漏, 图9为实验室采集到的泄漏数据。 图8 天然气管道泄漏检测模拟实验平台Fig.8 Natural gas pipeline leak detection simulation test platform 管道原始信号一般为复合信号, 且存在大量的背景噪音, 笔者将采集到的管道原始信号作为改进后的PSO-VMD的输入信号, 得到最优解k=5,α=1 563, 再作为VMD-ED的输入参数, 分解后各个模态分量的欧氏距离如表1所示。 表1 管道原始信号模态分量的欧氏距离 根据各模态分量概率密度函数的欧氏距离, 由式(17)~式(19)可计算出第3个分量与第4个分量之间的增量最大, 选取增量最大的两个相邻模态分量作为有效分量选取的转折点, 因此选取第1、2、3个模态分量, 对管道信号进行重构, 并计算重构信号的信噪比和均方误差作为性能评价指标。计算改进算法与VMD-CORR算法以及EMD-ED算法的管道重构信号的信噪比和均方误差, 其对比图如图10和图11所示。 图10 SSNR对比图Fig.11 MMSE contrast diagram 由图10可以看出, VMD-CORR算法和EMD-ED算法的重构信号的信噪比分别为13.511 0 dB、 13.353 6 dB, 而改进的VMD-ED算法重构信号的信噪比显著提高, 为20.441 8 dB。由图11可以看出, VMD-CORR算法和EMD-ED算法的重构信号的均方误差分别为0.060 6 dB、 0.061 7 dB, 均高于改进算法的0.027 3 dB。图10、 图11的SNR和MSE的结果对比, 验证了笔者提出的改进算法可以有效提高信号的信噪比, 降低均方误差, 能较好地处理复杂的管道信号, 验证了其在管道泄漏检测中的有效性。 针对VMD算法分解后有效模态分量选择困难以及去噪效果不理想等问题, 笔者采用一种改进PSO算法的VMD参数优化方法, 有效获取了参数组[k,α], 并与欧氏距离结合, 筛选有效的模态分量, 进行信号重构。通过对仿真信号和实验室管道采集信号进行试验, 结果表明该方法相较于其他算法, 有效提高了信号的信噪比, 且均方误差较小, 去噪效果更为显著, 验证了该方法在长输管道泄漏检测中应用的可行性。但此算法对VMD参数组优化所需时间较长, 可以根据该问题进行下一步研究。
5 实验与分析
5.1 改进PSO-VMD-ED算法的仿真实验分析




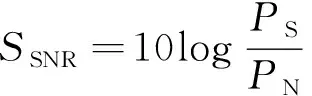


5.2 改进算法在管道泄漏检测信号中的应用



6 结 语

