改良式线性回归方法的企业信用评估机制

谢兆贤, 陈哲奇, 陆思诺, 黄沈权

(1. 曲阜师范大学 a. 软件学院; b. 物理工程学院, 山东 曲阜 273165; 2. 温州大学 机电工程学院, 浙江 温州 325027)

0 引 言

信用评分是指根据客户的信用历史资料, 利用一定的信用评分模型, 得到不同等级的信用分数。根据客户的信用分数, 授信者可以分析客户按时还款的可能性。据此, 授信者可以决定是否准予授信以及授信的额度和利率。虽然授信者通过分析客户的信用历史资料, 可以得到同样的分析结果, 但利用信用评分却更加快速、 客观, 更具有一致性。信用评分方法对贷款的信用风险进行评价, 以区分“好”或“坏”的信用贷款, 起因是当时美国的一些金融机构及直销公司在信用监管上出现了问题。对是否提供贷款或提供商品给申请人, 都是由信用分析人员对申请人进行分析和判断后做出决定。由于当时正处在第2次世界大战, 大批的信用分析人员都参军了, 信用分析人员极度缺乏。为此, 这些公司就组织信用分析人员将他们在进行信用分析时的一些基本准则汇编成册, 供没有经验的分析人员参考使用。当时, 美国有些银行开始进行一些有关信用评分方法的试验, 目的是提供一种可以处理大量信贷申请的工具。1956年, 工程师Fair和数学家Lsaac共同发明了著名的FICO(Fair Isaac Company)评分方法, 包含财务(FI: Finance)和控制(CO: Controlling)两个模块。并成立了Fair Isaac公司, 为世界上第1家提供信用评分数学模型的公司。1958年, Fair Isaac公司发布了第1套信用评分系统， 其客户大多数是金融机构以及直销公司。为了方便计算生活中的信用问题, 信息统计学家建立了信用评分模型。信用评分模型是一种传统的信用风险量化模型, 利用可观察到的借款人特征变量计算出一个数值(得分)代表债务人的信用风险, 并将被检测者归类于不同的风险等级。对个人客户而言, 可观察到的特征变量主要包括收入、 资产、 年龄、 职业以及居住地等； 对法人客户而言, 包括现金流量、 财务比率等。

信用评分技术用于甄别申请者的好坏, 并且评估各自的潜在风险, 在社会信用体系当中扮演着重要角色。对于构建信用评分系统过程, 有人以大数据技术挖掘历史信贷数据中的高价值特征, 进行鉴别高风险申请者[1-2]。

在现实生活中, 越来越多的事情会存在关联, 也就是事情与人的信用相关, 发展出以下几个问题。首先, 银行卡信用。银行对一个用户需要进行信用评估, 通过对客户的信用评估可以确定该客户的贷款额度, 还款期限等。这里的信用度计算值具有重要意义, 例如： 当一个客户长期拖欠欠款并且被证实无力偿还银行贷款时, 银行将减少对该客户的借款信用度, 直到他将欠款还清。

其次, 淘宝卖家信用。网购过程中, 淘宝会选择性的筛选质量好的产品, 并且将消费者对产品的评价进行整合, 通过大数据对卖家评分, 以便向消费者提供质量好与口碑好的卖家, 从而可以让消费者有更好选择。淘宝客服通过数据的整合和处理, 按照好评率给卖家进行评分, 该评分也在一定程度上体现了卖家信用。

最后, 信用资产。基于Liu[3]提出的具备自对偶性的可信性测度, 提出模糊条件在险价值(FCVaR)的应用。不仅对模糊市场的信用风险资产管理进行研究,而且给出信用风险的控制和资产优化组合的模糊规划方法,以供信用资产管理者采用[4]。

个人信用因为受到他人的主观意愿影响, 在进行信用评估时将会遇到很多问题, 例如： 移动电信数据的个人信用。然而, 企业信用比个人信用受到他人主观意愿的影响小很多, 因为企业针对的客户有限, 并不会因为无关系客户的评价而受到影响。因此, 企业信用的评价便显为更加可行与重要。

所以, 笔者对市场空白的企业信用度评估提出一种新的方法。通过对于制造型企业信用度的重新评估, 将信用这一抽象的概念具体化, 提出一个有效的信用度计算方法, 进行信用评估。通过改良式的线性回归法, 将制造型企业信用的好坏通过数值直观体现。笔者将传统的线性回归方法应用于直接计算企业的信用度过程, 并提出一些新的理解改进线性回归法, 有效应用于企业信用度的计算。通过具体数值的体现, 有效评估一个企业是否是信用优良企业, 对于社会发展具有重大意义与价值。

1 问题定义

假设一个制造公司的信用度是个可计算的值, 则其将受到制造公司的各个因素影响, 相关定义说明如下。

1) 制造历史。

定义1 制造历史。是指企业从刚成立开始, 所有从该企业出产的材料以及设备的情况。

定理1 残次品δ。在制造历史的过程中, 会出现残次品δ值, 表明是否影响生产因素的情况。当历史残次品越大, 意味着生产情况越差。通过企业的制造历史评判分数(x1)可以反映出企业的制造水平。假设企业制造历史的初始评分ν1max, 如果企业出现制造劣质的残次品, 导致企业的制造历史评分下降, 则每当出现有一次残次品时, 将企业制造历史下降评分(ν1)设定为2分, 表达式如下

x1=ν1max-δν1

(1)

例如： 假设企业制造历史的初始评分为100分, 一个企业在1个月内出现2次制造残次品的情况, 则制造历史评分下降到96; 若在下个月再次出现1次制造残次品的情况, 则该企业的制造历史评分(x1)下降到94分。

2) 供货(是否出现过延迟交货)。

定义2 供货。是一种合作方式, 根据进货和售出争取中间的差价, 是价格实现自身功能时对市场经济运行所产生的效果, 是价格的基本职能的外化。

(2)

3) 社会评价参数。

定义3 社会评价参数。是指所有客户对一个企业某一个产品的评价值, 此参数是一个常数, 是所有客户评价汇总的体现。其参数由客户进行打分, 网站对所有客户的分数进行综合, 得出一个常数参数。

定理3 社会评价参数σ。在企业间进行交易时, 不同的交易结果会导致社会或企业间的评价发生变化, 对这些评价评级评分, 得出平均值从而算出社会评价参数。社会评价参数σ越高意味着企业的社会口碑越好。

4) 企业的生产能力。

定义4 企业生产能力。是指在计划期内, 企业参与生产的全部固定资产, 在既定的组织技术条件下, 所能生产的最大产品数量, 或能处理的原材料数量。生产能力是反映企业所拥有的加工能力的一个技术参数, 它也可以反映企业的生产规模。

定理4 将一个企业的生产能力用分数定义, 将企业的生产能力初始评分定为ν3max分, 如果企业的生产能力由社会评价σ参数决定, 即表达式如下

x3=ν3maxσ

(3)

5) 服务满意度。

定义5 服务满意度。指出售后的服务, 即在商品出售所提供的各种服务活动后, 得到的反馈满意状况。其中包括了设备或材料的维修, 设备使用的技术指导, 设备材料的退货服务等。

定理5 售后服务时间μ。在企业完成被需求的订单后, 企业会被要求提供售后服务, 会出现企业售后服务时间μ, 当企业的售后服务时间越长, 说明企业提供的售后服务越好。将一个企业的客户服务满意度用分数(x4)定义, 假设服务满意度的初始评分(ν4max), 如果企业的售后服务时间每高于或低于市场平均售后服务时间(t)%, 则将企业的服务满意度评分上升或下降, 将服务满意度变化评分ν3设定为0.3分, 表达式如下

x4=ν4max+100×0.3(μ-t)/t

(4)

例如某企业的社会服务满意度评分为60分, 该企业售后服务时间为30 d, 市场的平均售后服务时间为20 d, 则该企业的客户满意度则为75分。

6) 材料价格的变化。

定义6 材料价格的变化。指的是企业对于同一物料或设备的定价在不同的时间内变化。

定理6 价格变化率κ。企业对物料价格进行调整时, 会出现一个和市场该物料的平均价格的差值(τ), 用价格变化差值除以物料市场平均价格, 可得到该物料的价格变化率κ, 价格变化率象征着物料价格在一定期间内变化的程度, 价格变化率越高则说明物料价格的变化越大, 这样对企业的信誉将有影响。将一个企业的物料价格用分数(x5)定义, 假设服务满意度的初始评分(ν5max), 将物料价格每变化1%物料价格变化评分(ν4)设定为2分, 表达式如下

x5=ν5max-2κ

(5)

2 模型与算法

2.1 线性回归模型

在统计学中, 线性回归(Linear Regression)是利用称为线性回归方程的最小平方函数对一个或多个自变量和因变量之间关系进行建模的一种回归分析。这种函数是一个或多个称为回归系数的模型参数的线性组合, 这些回归系数之间都有较强的联系性。当只有一个自变量的情况称为简单回归, 大于一个自变量情况的叫做多元回归(这反过来又应当由多个相关的因变量预测的多元线性回归区别, 而不是一个单一的标量变量)。线性回归模型常用于探讨连续结果与自变量之间的关系; 也可以使用二进制结果[5-6]。为了实现常态假设, 研究人员经常进行任意的结果转换。Eppinga等[7]在2017年使用基于秩的逆正态变换探索了身高与剥夺之间的关系。线性回归模型在讨论有较强联系的一个或多个因素的影响方面有很大的作用, 但文中的各个数据并没有非常强的联系[8]。他们互相影响但是没有起到决定性的作用, 于是笔者对线性回归模型进行了优化。

通过计算平均值的方法, 将一个企业的制造历史评分、 供货历史评分、 满意度评分、 生产能力评分和价格评分进行求平均值, 得出一个计算企业信用度平衡值π, 表达式如下

π=(x1+x2+x3+x4+x5)/5

(6)

2.2 模型

2.2.1 模型的符号与说明

2.2.2 回归分析

回归分析研究的主要对象是客观事物变量之间的统计关系, 它是建立在对客观事物进行大量试验和观察的基础上, 以寻找隐藏在不确定现象中的统计规律性的方法, 是在掌握大量观察数据的基础上, 利用数理统计方法建立因变量与自变量之间的回归关系函数表达式(称回归方程式)研究变量间相互关系的密切程度、 结构状态及进行模型预测的一种有效工具。

如果变量x1,x2,x3,…,xp与随机变量y之间存在着相关关系, 通常就意味着每当x1,x2,x3,…,xp取定值后,y便有相应的概率分布与之对应。随机变量y与相关变量x1,x2,x3,…,xp之间的概率模型为

y=f(x1,x2,…,xp)+ε

(7)

其中f(x1,x2,x3,…,xp)为变量x1,x2,x3,…,xp的确定性关系,ε为随机误差项。由于不同的因素之间的关系是错综复杂的, 一种因素的影响很难用有限个变量准确说明, 随机误差项可以概括表示, 由于人们的认识以及其他客观原因的局限而没有考虑的各种偶然因素。当概率模型式(1)中回归函数为线性函数时, 有

y=β0+β1x1+β2x2+…+βpxp+ε

(8)

其中β0,…,βp为未知参数, 常称它们为回归系数。当变量x个数为1时, 为简单线性回归模型, 当变量x个数大于1时, 为多元线性回归模型。

2.2.3 回归建模的过程

在实际问题的回归分析中, 模型的建立和分析有几个重要阶段, 如下以经济模型的建立为例。

1) 具体社会问题。问题应由多个因素构成, 这几个因素之间互相关联, 不同的因素之间互相作用互相影响, 可以对问题的结果造成不同的结果导向, 同时不同的因素所占用的权重也不尽相同, 有时影响较小的因素会被选择性剔除。

2) 根据研究的目的设置指标变量。回归分析模型主要揭示事物间相关变量的数量关系。首先要根据研究问题的目的设置因变量y, 然后再选取与y有关的一些变量作为自变量。在一般情况下, 希望因变量与自变量之间具有客观因果关系。尤其是在研究某种有可能互相影响导致结果不同的情况下, 必须根据具体的研究目的, 利用线性回归理论结合客观知识, 从定性角度确定某种经济问题中各因素之间的因果关系, 使结果更加准确。

3) 收集、 整理统计数据。回归模型的建立是基于回归变量的样本统计数据, 其中包括了所有可能对实验有影响的数据长期观察而得到的较为稳定的一般数据。当确定好回归模型变量后, 就要对这些变量收集、 整理统计数据。数据的收集是建立问题回归模型的重要一环, 是一项基础性工作, 样本数据的质量如何, 对回归模型的水平有至关重要影响。

4) 确定理论回归模型的数学形式。当收集到所设置的变量数据后, 就要确定适当的数学形式描述这些变量之间关系。绘制变量yi与xi(i=1,2,3,…,n)的样本散点图是选择数学模型形式的重要手段。一般把(xi,yi)所对应的点在坐标系上标出, 观察散点图的分布状况。如果n个样本点大致分布在一条直线的周围, 可考虑用线性回归模型去拟合直线。

5) 模型参数的估计。回归理论模型确定后, 利用收集、 整理的样本数据对模型的未知参数给出估计是回归分析的重要内容。最常用的未知参数估计方法是普通最小二乘法。普通最小二乘法通过最小化残差平方和而得到参数的估计值。即

minRRSS=∑(yi-hat(yi))×2

(9)

6) 模型的检验与修改。当模型的未知参数估计出后, 就初步建立了一个回归模型。建立回归模型的目的是应用其研究具体问题, 但如果直接应用这个模型做预测、 控制和分析不够慎重。因为这个模型是否真正揭示了被解释变量与解释变量之间的关系, 必须通过对模型的检验才能决定。统计检验通常是对回归方程的显着性检验, 以及回归系数的显着性检验, 还有拟合优度的检验, 随机误差项的序列相关检验, 异方差性检验, 解释变量的多重共线性检验等。如果一个回归模型没有通过某种统计检验, 或通过了统计检验而没有合理的经济意义, 就需要对回归模型进行修改。如果其中一个因素的显着度较小, 则必须对这个因素进行深入分析, 讨论这个因素的数据是否错误或无意义, 并对这些数据进行再次整合、 回归, 如果结果依然不变, 则选择删除这个因素, 并对剩下的因素重新计算, 得到新的方程, 通过再次显着性等检验, 直到得出完整而且正确的线性回归方程。

7) 回归模型的运用。当一个具体问题的回归模型通过了各种统计检验, 且具有合理的意义时, 就可以运用这个模型进一步研究具体问题。例如, 经济变量的因素分析应用回归模型对经济变量之间的关系做出了度量, 从模型的回归系数可发现经济变量的结构性关系, 给出相关评价的一些量化依据。通过模型分析, 可以从得到的结果中分别对于问题的构成因素分析和对问题未来的决策进行预测。

在回归模型的运用中, 应将定性分析和定量分析有机结合。这是因为数理统计方法只是从事物的数量表面去研究问题, 不涉及事物的规定性。如果要研究事物的本质就必须依靠专门学科的研究, 通过这个模型在实践中是否具有实用性才能下定论, 具体的模型建立如图1所示。

图1 回归模型建立Fig.1 Regression model establishment

3 模型计算和分析

模型分析使用IBM SPSS Statistics 24软件作为分析工具, 电脑处理器为Intel(R) Core(TM) i5-6300HQ CPU @ 2.30 GHz 2.30 GHz, 内存为8.00 GByte。

3.1 传统线性回归模型

假设一个制造公司的信用度是一个可以计算的值, 则其将受到制造公司的各个因素影响, 其中包括制造历史, 供货历史和生产能力, 顾客满意度以及价格变化, 通过以上5个因素, 就可以得到一个关于信用度的线性回归方程式, 如果将信用度设为P, 可得到

p=β0+β1x1+β2x2+β3x3+β4x4+β5x5+ε

(10)

通过计算可得到不同的关于工厂信用度的结果, 通过信用度计算结果和对样本企业的信用口碑评价横向对比, 可得出一个信用范围, 即在该范围内, 企业信用被分为优, 良, 差3个等级。一般将评分为100～85的企业评为优企业, 84～70之间的企业定义为良企业, 将信用度低于70的企业定义为差企业。

笔者采用SPSS(Statistical Product and Service Solutions)线性回归方法, 通过仿真手段, 对得到的十家企业的制造历史(是否有过残次品)、 供货、 生产能力、 材料的价格变化、 售后服务、 和进行评估, 根据该公司不同时期的表现进行打分, 最终汇总成一个信用度, 如表2所示。将数据导入SPSS软件进行处理, 得到结果列于表3。

表1 符号说明

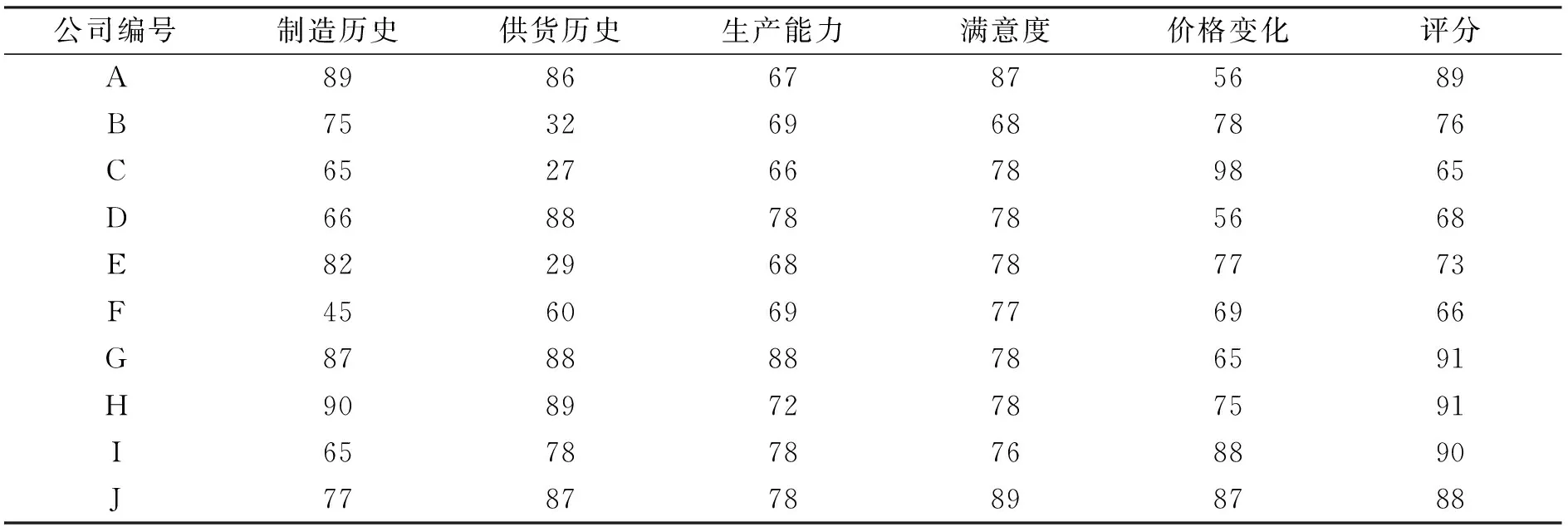
表2 企业信用的评分

从表3可知, 标准差估值的误差为4.418, 可以看出公式的误差较小, 可作为信用度的评估标准。

表3 传统线性回归模型摘要

相关系数R的绝对值为0.968, 决定系数R2为0.937, 表示自变量所能解释的方差在总方差所占的百分比, 取值越大说明模型的效果越好。调整后的R2为0.859, 但所占的百分比仍然是一个较大的值, 因此说明这些数据对于信用度计算有重要意义。

从表4可知, 回归系数检验在方差分析结果中F=11.950, 该方程的显着性的绝对值为0.016, 一般认为, 显着性小于0.05时, 方差不具有齐性, 说明变量存在差异, 适合回归； 线性回归的平方和的总计为1 116.1。

表4 传统线性回归ANOVA方差检验表

表5的标准化系数B, 代表了在该回归方程中, 各个变量对因变量的解释力度。从表5中的标准化系数可以看出, 显着性检验是对系数的显着性的检验, 对常量的显着性为0.285, 因此可以看出对常量存在的假设是正确的, 从而可以看出β1=0.345,β2=0.292,β3=0.187,β4=-0.293,β5=0.096,ε=38.689关于企业信用度p的表达式如下

表5 传统线性回归系数表

p=0.345x1+0.292x2+0.187x3-0.293x4+0.096x5+38.689

(11)

3.2 改良型线性回归模型

通过对原始的线性回归模型的修改, 得到关于信用度新的计算方法, 表达式如下

p=β0+β1x1+β2x2+β3x3+β4x4+β5x5+ε+β5π

(12)

同时对原企业信用评分表格进行修改, 得到结果列入表6。将数据导入SPSS文件, 得到结果列入表7。

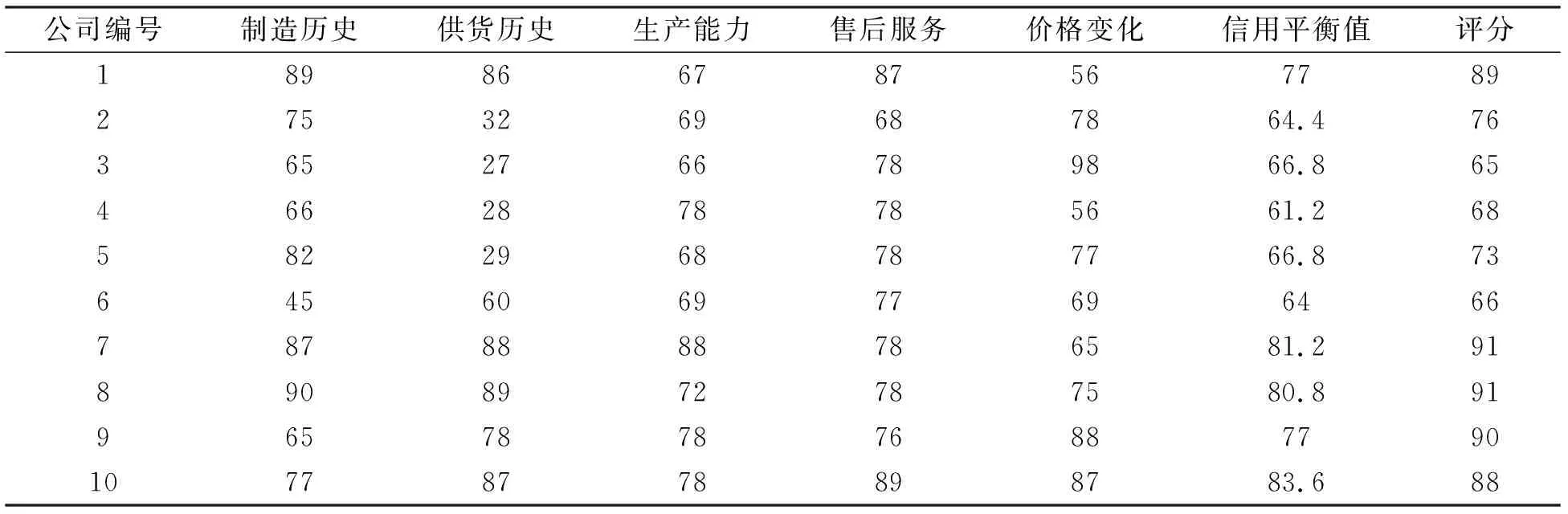
表6 引入信用平衡值后企业信用评分表

表7 改良线性回归模型摘要

其中供货历史因素被认为是无关变量, 被系统排除。所以得到新的方程式, 表达式如下

p=0.053x1-0.105x3-0.585x4-0.196x5+1.459π+38.689

(13)

经回归系数检验, 修改后的线性回归与表4一致, 具备一致性。可以推断出在引入企业信用平衡度后变量依然存在线性关系, 仍然可以进行回归分析。

由于企业信用平衡度是由以上5项的平均值得到的, 在失去供货历史的情况下无法得到, 在表8中, 企业信用平面度的权重显着性仅为0.013, 远小于其他影响因素。权重显着度越低说明该因素对最终的计算结果影响越小, 企业平衡信用度也可以作为一个无关变量删除。因此最终决定将制造历史、 生产能力、 售后服务和价格变化作为影响企业信用度的计算因素, 将他们统计为表9, 将表9中的数据导入SPSS软件进行计算, 得到表10～表12的结果。

表8 改良线性回归系数表

表9 影响企业信用度因素表

表10 二次改良线性回归模型摘要

从表10中得知, 标准差估值的误差为3.865, 误差较小, 可以作为信用度的评估标准。相关系数R的绝对值为0.805, 决定系数R2为0.648, 表10中的值虽然小于表3中的值, 但是由于他们均大于0.5因此依然具有计算意义。表明这些数据对信用度计算有重要意义。从表11中可知, 回归系数检验, 在方差分析结果中,F=11.950, 该方程的显着性的绝对值为0.023。一般认为, 显着性小于0.05时, 方差不具有齐性, 说明变量存在差异, 适合回归； 线性回归的平方和的总计为1 116.1。由表12可以看出, 制造历史、 生产能力、 售后服务和材料价格的显着性均较强, 因此他们可以作为体现企业信用度的计算因素, 通过它们的权重系数β1=0.470,β2=0.629,β4=0.325,β5=0.109,ε=-34.859, 关于企业信用度p的表达式如下

p=0.47x1+0.629x2+0.325x4+0.109x5-34.859

(14)

表11 二次改良线性回归ANOVA方差检验表

表12 删去平衡常数回归系数表

3.3 传统线性回归模型与改良线性回归模型对比

对比传统的线性回归方法, 在添加新的参数信用平衡值后, 相关系数R、 绝对系数R2和方差显着性并没有发生变化。因此, 优化的结果可作为一种新方案。同时, 在传统线性回归系数表中, 供货历史系数的标准化系数权重偏高, 但它所对应的权重显着性确是所有因素中最小的。由此推断出供货历史参数, 于计算企业信用度的准确性, 存在较大的负面影响。在新建立的方程消除原先的方程可能产生一定的错误, 体现出供货历史是一个无关变量。当选择将这个变量除去, 会使内容更加严谨, 优化了方程, 使结果更加具有说服力。笔者改良的线性回归法, 由于信用平衡度所占的权重显着度过小, 因此对方程进行再一次精简。对传统线性回归模型所需要的5个要素进行了优化, 最终得出以制造历史、 生产能力、 售后服务和材料价格为影响因素的企业信用度计算方法, 减少计算复杂性。

4 结 语

笔者通过线性回归的方法计算出企业信用度, 将线性回归法进行了改进, 使线性回归法计算的企业信用度更加真实。

通过模拟发现, 线性回归在变量选择和分类效果方面都具有优势。此外, 将笔者的模型应用于制造型企业的信用评分中, 通过现实生活中真实的企业数据实证分析, 检验整合模型在实际应用中的效果。研究结果显示, 整合模型在实际应用中有很好的表现。需要说明的是, 笔者所提出的模型虽然主要应用于制造型企业信用评分中, 但是仍可以扩展到多个地区的信用评分模型, 也可以应用到多源数据融合的分类建模问题。