基于Logistic算法的考研成绩变量预测方法

李 楠, 郝文佳

(桂林理工大学 环境科学与工程学院, 广西 桂林 541006)

0 引 言

从历年研究生考试的报名情况看, 报考硕士研究生的学生人数持续增加, 2018年我国研究生报名人数为238万人, 2019年为290万人, 比上一年增加52万人, 中国研究生教育已经进入了新的历史发展阶段[1]。考研成绩的预测可以预估考生的考试成绩, 并为考研的下一个程序阶段做准备。由于考研成绩与多个成绩变量有关, 因此为了保证考研成绩结果的预测精度, 需要提出一种高精度考研成绩变量预测方法。

教育部在2012年发布了考研成绩的相关报告, 对考研成绩统计工作产生了深远的影响。但对考研成绩数据的预测和研究工作起步较晚, 相关研究文献较少。目前对考研成绩变量预测方法的研究成果主要包括多变量GM(1,N)灰色模型成绩预测方法、 正交核最小二乘法成绩预测方法和权重分配组合模型成绩预测方法等。然而在成绩变量预测问题的研究上仍存在缺陷有待改进, 例如仅凭学生的单一成绩数据对考研成绩进行预测、 历史数据的获取来源过于单一等[2]。为解决上述传统方法存在的问题, 在前人研究已取得重大成果的基础上进一步探索, 笔者提出了基于Logistic算法的考研成绩变量预测方法, 该方法主要立足于Logistic算法, 即回归分类模型, 与传统的分析手段不同, 其将考研成绩变量的诸多影响因素按照不同的逻辑层次进行划分, 凸显出不同层次影响因素的主次效应, 得出更加精准的考研成绩变量预测结果。

1 考研成绩变量预测方法设计

考研成绩变量预测方法在设计过程中引入了Logistic算法, 并以该算法的运行原理为基础构建对应的回归分类模型。以某学生的历史学习数据以及历年考研的成绩数据作为初始数据, 通过模型的运算得出考研成绩变量的变化规律, 结合考研成绩变量的影响因素得出最终的成绩变量预测结果, 并实现该预测方法的设计目的。

1.1 收集历年考研成绩数据

历年考研成绩数据的采集是为了获取研究所需的学生基础信息数据以及历史成绩数据, 其中学生的基础信息数据包括学生的学号、 年龄和性别等, 由于信息系统中学生信息的精确度较低, 不能满足技术要求, 因此运用python工具编写一个网络爬虫程序, 通过学生的身份证号在相关平台上进行历史数据信息的抓取, 并从抓取到的文件中对此次研究中需要使用的信息数据进行解析, 最终获取到可以满足成绩变量预测方法研究要求的学生历史信息数据[3]。经过历年考研成绩数据的收集, 得出的考研学生基础数据的部分采集结果如表1所示。

表1 考生基础数据属性表

学生的历史成绩数据方面, 从教务部门获得该学院所有专业多个学年的成绩排名数据, 去除与此次研究无明显关联的字段属性, 得出学生历史成绩数据属性结果, 如表2所示。

表2 学生成绩数据属性表

除了上述学生对象的历史成绩数据外, 还需要对历年的考研平均数据进行收集与统计, 并以采集整理完成的结果作为考研成绩变量预测的初始数据[4]。

1.2 数据预处理

(1)

(2)

其中M为初始数据集中的平均值或中位数,n为初始数据集中数据的数量[7]。最后从属性规约和数值规约两个方面实现对初始数据集的规约处理, 并得出预处理完成的考研成绩初始数据表, 如图1所示。

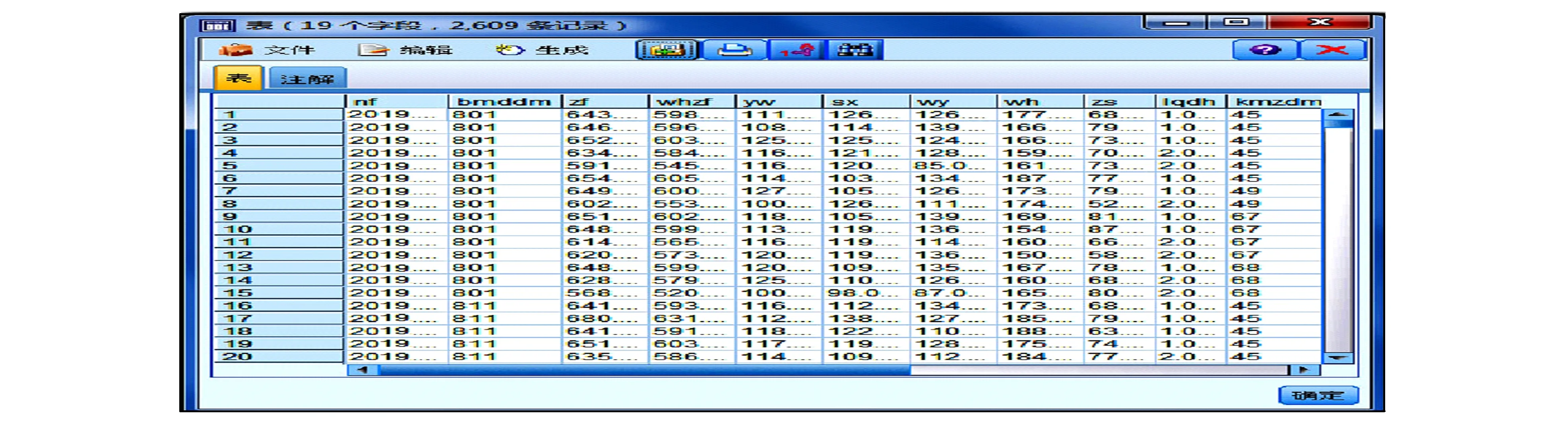
图1 初始数据预处理显示结果Fig.1 Initial data pre-processing results

1.3 设置考研成绩变量

以预处理完成的初始数据为基础, 结合数据内容分析结果与数据特征提取结果, 设置考研成绩预测变量[8]。在本次预测方法中设置的考研成绩变量分别为平均成绩绩点、 高数加权平均成绩、 专业课成绩和四六级加权平均成绩, 其中平均成绩绩点是评估考研成绩的一项重要指标, 该变量的计算公式如下

(3)

其中GPA为平均成绩绩点,fi和gi分别为课程学分和课程绩点,gi的计算表达式为

(4)

其中F为学生的实际考研科目总分数[9]。加权平均成绩是学生每门考研成绩与其权值比例的乘积计算出的平均成绩, 其计算表达式为

(5)

其中Fi为加权科目分数,WA为单科考研的加权平均成绩。通过式(5)的计算可得出高数、 政治以及英语四六级的加权成绩计算结果。而专业课成绩可以通过数据调取直接得出, 为提高数据的参考价值, 可以计算专业课的平均值代替某一次专业课的实际成绩。

1.4 构建Logistic回归分类算法模型

Logistic回归分类算法模型的构建是用于描述分类响应变量与解释变量之间的关系, 在本研究中也就是历史考研成绩、 学生平时成绩与考研成绩之间的变量关系[10]。定义模型中的响应变量为Y, 且该变量只有0和1两种取值结果, 假设Y依赖于p个自变量, 记为Xi, 则在自变量的作用下Y取值为0或1的概率可表示为

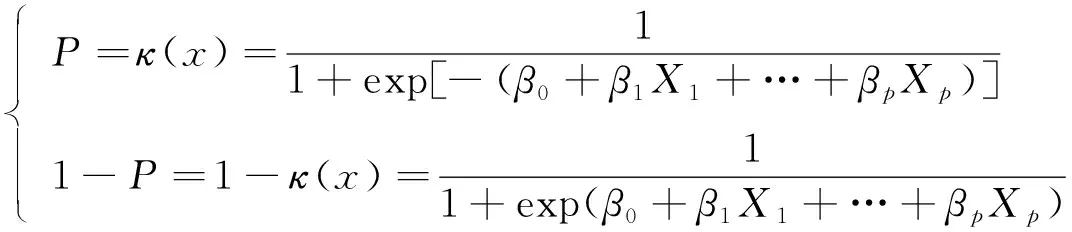
(6)

式(6)为Logistic回归分类算法模型的一般形式, 其中βi为模型的回归系数, 当i的取值为0时,β0为常数项, 得出的Logistic回归分类算法模型建立结果如图2所示。

图2 Logistic回归分类算法模型框图Fig.2 Logistic block diagram of regression classification algorithm

判断一个变量是否能对相应变量提供显著的附加解释信息, 若满足则将该变量选入Logistic回归分类算法模型当中, 否则剔除该变量。通过模型变量的筛选, 得出模型对应的Logistic回归分类函数如图3所示。

从图3中可以看出, Logistic函数的值域为[0,1], 保证了模型概率估计的合理性。受到自变量变化的影响, 响应变量的概率值也发生了变化[11]。则将影响考研成绩变量的影响因素作为模型的输入值代入模型中, 模型的输出值即为成绩变量回归分类的结果。

1.5 分析考研成绩的影响因素

影响考研成绩的因素可以分为个人因素、教学因素、环境因素以及专业因素等, 其中个人因素是考生的学习状态、 对专业知识的理解程度以及对专业知识的应用能力等[12]。教学因素是考生在考研学习阶段接受的教学水平, 具体包括教师的教学水平、 教学资源的数量以及教学资源的来源等。环境因素主要是生源地因素和接受教育环境的因素, 不同地区的考研政策以及接收条件不同, 不同生源地考题的难易程度也有所区别。而专业因素是学生报考的专业是否与当前接受教育的专业有关, 与必考科目, 即高数、 政治以及英语科目的关联程度。综合所有考研成绩的影响因素, 并将其作为Logistic回归分类算法的自变量导入构建的模型中, 得出对应的响应变量, 即考研成绩变量的概率测算结果。

1.6 实现考研成绩变量预测

通过对历史考研成绩数据以及学生成绩数据的分析与特征提取, 得出考研成绩变量在无影响因素作用下的变化规律。然后利用Logistic回归分类算法模型, 分析影响变量与考研成绩变量之间的关系, 综合两个分析结果得出考研成绩变量的预测结果。多个考生的成绩变量数据, 通过对数据集的遍历得出多个模型输出结果, 并选择概率值最高的分类数据作为考研成绩变量的预测结果。

2 对比实验分析

2.1 选择考研研究对象

以全国256个地级及以上城市的1 195所本科高等学院获得各个城市本科高校生作为此次实验的研究对象。选择的研究对象为具有考研意愿的大四学生, 由于生源地对考生的成绩存在着一定的影响, 因此在选择考研研究对象时, 需要将考生的生源地信息一同存储到主测环境中, 作为实验的自变量之一。通过对学生数据的筛选最终确定实验研究对象共7 642人, 具体的研究对象统计情况如表3所示。

表3 考研研究对象统计表

2.2 样本数据来源

针对选择的实验研究样本, 调取每个考生在校期间的成绩, 需要调取的成绩包括四六级成绩、 英语成绩、 高数成绩、 政治成绩和专业课成绩, 并在主测环境中生成对应的初始数据, 如图4所示。

图4 考研成绩样本数据源Fig.4 Sample data source for postgraduate examination

除了研究对象的平时成绩外, 还需要调取不同生源地近5年不同专业的考研成绩, 包括考研的平均成绩以及考研的分数线等。按照相同的方式导入到实验环境中, 并生成对应的数据库表。

2.3 实验过程

对比设计基于Logistic算法的考研成绩变量预测方法与现有预测方法之间的预测误差, 凸显设计的考研成绩变量预测方法的应用价值。为了保证实验结果的可信度, 在实验中分别设置传统的考研成绩变量预测方法和文献[5]中的基于正交核最小二乘法的成绩预测方法作为此次实验的两个对比方法, 其中传统的预测方法是通过分析历年考研成绩变量的变化趋势, 得出对应的变化规律, 从而得出预测结果。而文献[5]中的预测方法, 在传统预测方法的基础上应用了正交核最小二乘法, 通过该技术方法的应用, 分析历史考研成绩数据与成绩变量之间的关系, 得出最终的成绩预测结果。分别将3种预测方法导入到相同的实验环境中, 并连接初始样本数据, 保证预测方法可以实时调用样本数据。设置考研成绩变量的实际预测数据, 其中部分考研成绩变量的数据设置情况如表4所示。

表4 考研成绩变量数据设置表

将3种方法的预测结果与设置的数据做对比, 可以得出有关考研成绩变量预测误差的实验结果, 其中设计的考研成绩变量的预测输出结果如图5所示。

图5 考研成绩变量预测界面Fig.5 Prediction interface of grade variables

2.4 预测结果对比分析

预测对比结果, 其中样本序号1的预测对比结果如表5所示。

表5 考研成绩预测对比结果

从表5可以看出, 在实验样本1中应用传统的成绩变量预测方法, 得出的平均预测误差约为0.58, 而应用文献[5]中提出的以及本设计的成绩变量预测方法, 对应的平均预测误差分别为0.57和0.56。使用相同的测试方法得出本次实验中7 642个样本的平均预测误差, 通过对比传统预测方法和文献[5]中预测方法的平均预测误差分别为0.65和0.62, 而笔者预测方法的平均预测误差为0.54, 由此可见设计预测方法的预测准确性更高。其原因是所设计预测方法综合所有考研成绩的影响因素, 并将其作为Logistic回归分类算法的自变量导入到构建的模型中, 得出对应的响应变量, 即考研成绩变量的概率测算结果, 在一定程度上, 有助于提高预测结果准确性。

3 结 语

大学生毕业去向的选择不仅对大学生自身非常重要, 同时也是国家、 社会、 高校十分关注的问题。考研首先要符合国家标准, 其次按照考研进度, 分别完成与学校联系、 报名、 初试、 调剂、 复试、 复试调剂以及录取等程序。考研成绩是决定大学生能顺利拿到研究生学位的重要决定因素, 考研成绩按照不同的报考专业, 对应的计算方式不同, 考研的必考科目包括专业课、 英语、 数学和政治, 此外, 其他专业课均为招生自主命题、 阅卷。考研成绩变量的预测可以在一定程度上影响考生的实际成绩, 通过Logistic算法的应用解决了变量单一的问题, 从实验结果看能有效地提升对考研成绩变量预测的准确度, 因此设计的基于Logistic算法的考研成绩变量预测方法可以推广使用。