深海遥控无人潜水器脐带缆动态特性及张力抑制方法

王海龙,张奇峰,崔雨晨,3,刘相斌

(1.中国科学院沈阳自动化研究所 机器人学国家重点实验室,辽宁 沈阳 110016;2.中国科学院机器人与智能制造创新研究院,辽宁 沈阳 110169;3.中国科学院大学,北京 100049)

目前,除“海沟”号外绝大部分深海遥控无人潜水器(Remotely operated vehicle,ROV)的脐带缆均为钢丝反螺旋铠装,脐带缆在母船与ROV之间起到能源供给、信息传输和物理连接等重要作用。由于受母船升沉、海流流速和自身材料特性等多重影响,脐带缆在水下的动力学特性极其复杂。如何从机理上揭示脐带缆的动态特性,并针对高张力情况提出有效措施,是当前ROV走向深海作业所需解决的关键问题。

目前,针对水下系泊系统、拖曳系统和ROV铠缆系统等水下缆索动力学建模主要有3种方法:有限差分法、高阶有限元法和集中质量法。Driscoll等人提出由粘弹性单元组合形成的单维集中质量缆模型,仿真和试验结果表明:该方法能较好地预测不同海流激励下ROV中继器的水下运动及铠缆内部张力变化[1]。Buckham综合考虑水下缆索弯曲、扭转等几何非线性因数影响,基于集中质量法建立了三维脐带缆动态力学模型,实验结果表明:该模型能较好捕获缆索低张力状态[2]。Koh采用有限差分法建立了脐带缆动态力学模型,对其进行动力学性能分析,并搭建试验平台,通过振动试验验证了所建立模型的正确性[3]。Gobat等人基于有限差分法建立了水下缆索的动力学模型,并采用隐式时间积分算法和自适应步长进行时域数值仿真,分析了二维缆索静、动态效应[4]。Huo等基于Euler-Bernoulli 梁理论建立了ROV脐带缆的动力学模型,并利用隐式中心差分法对其进行离散求解,利用该模型分析了脐带缆与ROV耦合系统动态特性,以及近ROV端脐带缆局部区域系缚浮球对缆内张力的影响[5-6]。

就水下缆索建模而言,集中质量法忽略了节点间弯曲和扭转,仅考虑弹性因素的影响,属于低阶有限元法;有限差分法不适合处理低张力缆索问题,因为该算法在零张力时会出现数值奇点;高阶有限元法具有完整的物理意义和理论基础,能够很好模拟缆索低张力动态特性。受母船升沉影响,ROV脐带缆在水下呈现高低张力交替变化的运动状态;同时,受海流的影响,脐带缆在水下做大幅度的三维运动,其运动状态具有大位移、小应变的动态非线性特征,其动力学建模更适合采用高阶有限元法。综合上述分析结果,本文基于几何精确梁理论对“海星6000”水下铠缆系统进行动力学建模,获得下潜过程中铠缆内部张力变化,并通过合理的系缚浮球,从而降低高海况下深水铠缆系统的高张力波,确保“海星6000”能够下潜到6 000 m级深度,并能在此区域安全作业[7-8]。

1 “海星6000”铠缆系统

“海星6000”是一套深海有缆遥控作业装备,主要用于在6 000 m以内海域开展海洋环境要素测量、原位观测及采样等科学考察[9]。该系统由潜水器本体、脐带缆、收放装置、动力单元以及操纵控制台等部分组成,如图1所示。传统ROV一般通过中继器与水面相连,这种方式在回收过程中存在一定风险,若母船升沉幅度较大,则母船、中继器和ROV三者之间的运动不同步现象,将导致脐带缆承受较大的冲击载荷使铠缆断裂。因此,“海星6000”采用无中继器模式,母船直接通过脐带缆与潜水器相连[10-11]。“海星6000”所使用的脐带缆为反螺旋钢丝铠装缆,单位长度水下重量0.953 kg,如不考虑铠缆在海流作用下的水下变形,当潜器下潜到5 604 m深度,水面下铠缆自身重量已超过了其安全工作载荷53.4 kN,无法满足下潜到6 000 m级深度的需求,而且由于铠缆受自身刚度影响,具有一定弹性,会起到放大母船升沉运动的作用,潜水器在水下的升沉运动幅度比母船大,同时,两者相位存在延迟,当延迟较大时,会在脐带缆内部产生冲击载荷,导致脐带缆内部出现较强的应力波,严重时会造成脐带缆和潜水器的损坏。图2所示的张力曲线取自“海星6000”第一次海试中第5潜次,ROV下潜深度为4 613 m。由图2可知,铠缆首端(近绞车端)张力峰值已接近铠缆的安全工作载荷,如果潜水器继续下潜到5 000～6 000 m级深度,很有可能超过脐带缆的安全工作载荷造成铠缆损坏,因此,有必要对深海科考型ROV铠缆系统的动力学特性进行研究,并采取有效措施降低铠缆张力。

图1 “海星6000”工作原理图

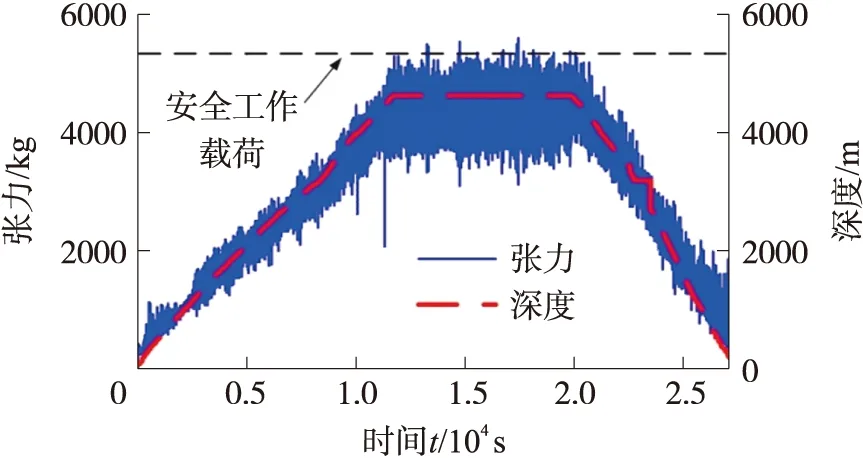
图2 铠缆首端张力波动曲线

2 脐带缆动力学建模

目前针对水下拖曳系统、系泊系统和深海ROV铠缆系统等水下缆索等数值分析法主要分为集中质量法、有限差分法、有限段法和有限元法。其中集中质量法属于低阶有限元法,仅考虑拉伸和弹性,无法处理低张力弯曲问题;有限差分法将微分方程转化为差分方程来求解,大量应用于流体力学问题。有限元法将无限自由度的连续问题进行离散,在缆索建模上,能处理较复杂的几何形状,且模块性能好,应用广泛。由Reisser[11],Simo[12-13],Ibrahimbegovic等[14-16]所提出几何精确梁理论,所描述的应变—位移之间关系是精确的非线性,可应用于小应变、大位移对象的动力学建模[17]。本节将采用几何精确梁理论对“海星6000”铠缆系统进行有限元模型建立。

2.1 脐带缆运动学

在进行运动学分析之前,首先对脐带缆进行一定简化,假设脐带缆材料连续,且初始状态为直线,横截面为圆形,如图3所示;图中黄色部分为铠缆系缚的浮力材料,本文将浮力材考虑为缆索外部节点。为分析方便,定义如图3所示的3个坐标系,分别为:大地坐标系、材料坐标系和运动坐标系[18]。大地坐标系{Ei}为惯性坐标系,坐标设为{E1,E2,E3};{ei}为材料坐标系,坐标设为{e1,e2,e3},e1与缆索初始状态的中线相切,e2,e3位于缆索的初始横截面。{ti}为运动坐标系,初始状态与材料坐标系{ei}重合。

图3 铠缆三维运动学描述

脐带缆在变形过程中符合Reissner-Timoshenko运动学假设,即初始状态下垂直于缆轴线的横截面在变形过程中始终为平面。由于受剪力作用,变形后脐带缆中轴线的切线并不一定与横截面保持垂直关系。上述所定义3个坐标系满足以下关系[17]

Ei(s)=R0(s)ei,ti(t,s)=R(t,s)Ei(s)

(1)

式中:s代表弧长,t代表时间,R0与R为正交转动张量算子,满足RRT=I。其中R0和R代表初始和当前转动张量算子,分别表征从固定空间坐标系{Ei}到材料坐标系{ei}、材料坐标系{ei}到运动坐标系{ti}的转换关系。

由罗德里格斯公式推导得到张量算子R与总转动矢量Ψ之间的函数关系为

(2)

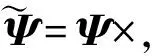
x(t,s)=xc(t,s)+X2t2(t,s)+X3t3(t,s)=

xc(t,s)+RE

(3)

式中:E=X2E2+X3E3,xc(t,s)为脐带缆中轴线的位置矢量。

脐带缆位置矢量的空间虚位移可表示为

(4)

式中:Θ称为转动矢量增量。对式(3)求二阶导数得

(5)

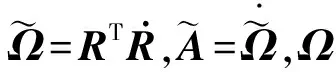
2.2 脐带缆三维动力学方程弱形式

在建立脐带缆动力学模型时,同样将其分成系缚浮球和无系缚浮球两种情况,将几何精确梁理论的运动学假设代入到连续介质力学动量定理,由虚功原理得到脐带缆变形过程中运动方程的等效弱形式,作为脐带缆动力学有限元模型建立的基础。

虚功原理公式可表示为

(6)

式中:q=(d,ψ)为广义位置矢量;Gext、Gint、Gacc分别为外力、内力和惯性力作用虚功项。负号表示外力虚功项与内力和惯性力虚功项的方向相反,下面将详细介绍3个虚功项的具体推导过程。

外力虚功项是指由外界力的作用而产生的虚功,这里的外力包括面力、体力和集中力3种,为分析方便,本文将集中力看作为作用在微小面积上的面力。则脐带缆的外力虚功项可表示为

(7)

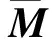
(8)

总的内力虚功项的显式表述为

(9)

式中:N和M分别代表单位弧长的材料应力和应力偶矢量,Γ和ΚR分别代表材料的应变与曲率矢量,δε计算公式如下

(10)

假设脐带缆和浮球的材料各向同性,且满足线弹性关系。引入线性本构方程描述材料的线弹性关系可表示为

N=CnΓ;M=CmKR

(11)

式中:N和M分别代表合应力和合应力偶矢量、Γ为材料应变矢量、KR为曲率矢量。

材料的轴向和弯曲弹性模量张量可表示

(12)

式中:EA和GJ分别为轴向和扭转刚度,GA2和GA3为缆截面沿惯性主轴方向的剪切刚度,EI2和EI3为缆截面的弯曲刚度;截面A2和A3包含了剪切修正系数。以上6个参数每个均包含两组:脐带缆和脐外挂浮球的材料参数。

水下脐带缆的惯性力虚功显式表示

(13)

加速度力Facc又可以分成两部分Facc,a和Facc,b

Facc=Facc,a+Facc,b=

(14)

(15)

2.3 铠缆系统的三维流体水阻力

深海ROV的铠缆系统在水下受到的外力一般包括:重力、浮力、水阻力和附加质量力。其中水阻力和附加质量力分别与铠缆的移动速度和加速度相关。下面分别给出单位长度水下铠缆和铠缆与浮力材料复合体的外力计算公式。

单位体积铠缆的重力矢量可表示为

(16)

式中:ρC和ρCB分别代表脐带缆和脐带缆与浮球复合体的密度;ρw为海水密度,g0是重力加速度矢量。虽然脐带缆和浮球由于受海水压力的作用体积可能发生变化,但所引起的密度变化非常小,基本可以忽略;因此,假设材料变形前后的密度相同。

铠缆在水下运动受到的水动力非常复杂,虽然可通过CFD数值仿真的方法获得水动力参数,但效率很低,因此最好采用经验公式的方式。通过检索文献,如忽略涡流脱落的影响,计算水动力参数可采用半经验公式,如Morison公式。

V=v2(h)e2+v3(h)e3

(17)

由此可得,水流流速矢量在运动坐标系下{ti}下的分量为

(18)

式中:下标1、2和3分别与t1、t2和t3轴对应,表示3个基矢量方向的流速分量,则脐带缆相对于水流的移动速度在运动坐标系{ti}下可表示为

(19)

此时单位缆长所受的水阻力在运动坐标系{ti}的分量为

(20)

式中:CCD1、CCD2和CCD3分别为脐带缆切向、法向与副法向的水阻力系数;CCBD1、CCBD2和CCBD3分别为脐带缆与浮球复合体切向、法向与副法向的水阻力系数。

在空间坐标系下表示单位缆长受到的水阻力为

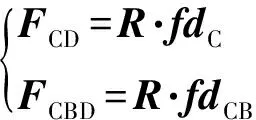
(21)

由式(16)和(21)得到,单位长度脐带缆所受的总外力为

(22)

3 有限元离散化

3.1 完全拉格朗日列式的线性化

由式(15)可知,脐带缆动力学方程具有高度非线性的特点,很难直接求得解析解。针对该类方程,通常采用迭代校正的方法逐步逼近真实解,常用的方法有Newton-Raphson法。因此,首先需要对弱形式的完全拉格朗日列式进行线性化,通过对式(15)求导,得到整个虚功项的线性部分如下

(23)

式中:下标“0”表示在t=t0时刻的状态量。其中等号后面3项依次代表给定状态下的残值和线性增量。下面将分别对各项进行线性化。

由式(23)可得外力虚功项线性化的一般表述为

lin[Gext(q,δq)]=Gext,0+DqGext,0Δq=

(24)

式中:Kext为切向刚度张量,其表征大位移情况下外力负载变化所引起切向刚度张量的变化。因缆索在水下运动受到外力包括保守力与非保守力,其中保守力为重力和浮力,非保守力为粘性水阻力。因此对外力虚功项线性化得到的切向刚度张量Kext也应包括保守与非保守两部分。由分析可知,非保守力对于载荷刚度矩阵贡献较小,为分析方便,本文忽略了载荷刚度矩阵非保守力部分。

由式(23)可得,脐带缆内力虚功项线性化的一般表述为

(25)

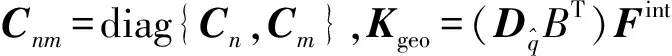
惯性力虚功项一般表述为

(26)

式中:M为质量张量;Kcent和Cgyro分别为离心力和哥氏力张量,这两个量对于脐带缆动力学影响较小,除了缆高速旋转的情况下可忽略。

3.2 线性弱形式的有限元离散化

本节通过有限元法对线性化后的结果进行离散。采用ne=2节点线性插值等参单元,对广义位移矢量进行离散

(27)

线性等参插值形函数在局部坐标系ξ下可表示为

(28)

对应的形函数导数为

(29)

由于

(30)

因此,形函数对整体坐标s的导数为

(31)

局部与整体坐标间的雅克比矩阵转换关系为

(32)

采用人为插值可以得到虚拟应变的离散近似值

(33)

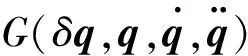
(34)

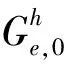
(35)

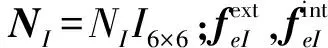
(36)

式中:

(37)

为了避免膜闭锁现象的发生,采用一点高斯积分计算缆索内部节点力、外力和切向张量,采用两点高斯积分计算加速度力和矩阵,由式(34)、(35)和(36)可得

(38)

这里的单元残余节点力为

(39)

由式(38)可得对应的单元有限元方程为

(40)

按照线性有限元中的组装方法,对单元进行组装得到总体有限元方程为

(41)

3.3 线性弱形式的有限元离散化

上述所讨论的问题属于数学上的边界值问题,为了求解该类方程,需给出一定的约束作为边界条件。针对深海ROV脐带缆系统,铠缆通过甲板上的绞车进行收放,如忽略绞车的旋转,脐带缆首节点的运动应与母船的运动一致。可将母船的运动作为脐带缆动力学求解的边界条件

(42)

脐带缆末端直接与ROV蘑菇头相连,因而,其边界条件为潜器的动力平衡方程。ROV在水下受到自身重力、浮力、水阻力和脐带缆拉力的共同作用,其动力平衡方程为

(43)

图4 “海星6000”ROV

4 铠缆局部系缚浮球动态特性研究

在动力学建模的基础上,利用FORTRAN语言编制有限元分析程序,数值算法采用广义α算法求解。然后利用该模型对“海星6000”ROV铠缆系统进行动力学性能分析。“海星6000”ROV结构如图4所示,其最大设计潜深6 000 m,空气中重量3.2 t,尺寸为1.6 m×3.2 m×2.6 m,其所采用的铠缆主要技术参数如表1所示。

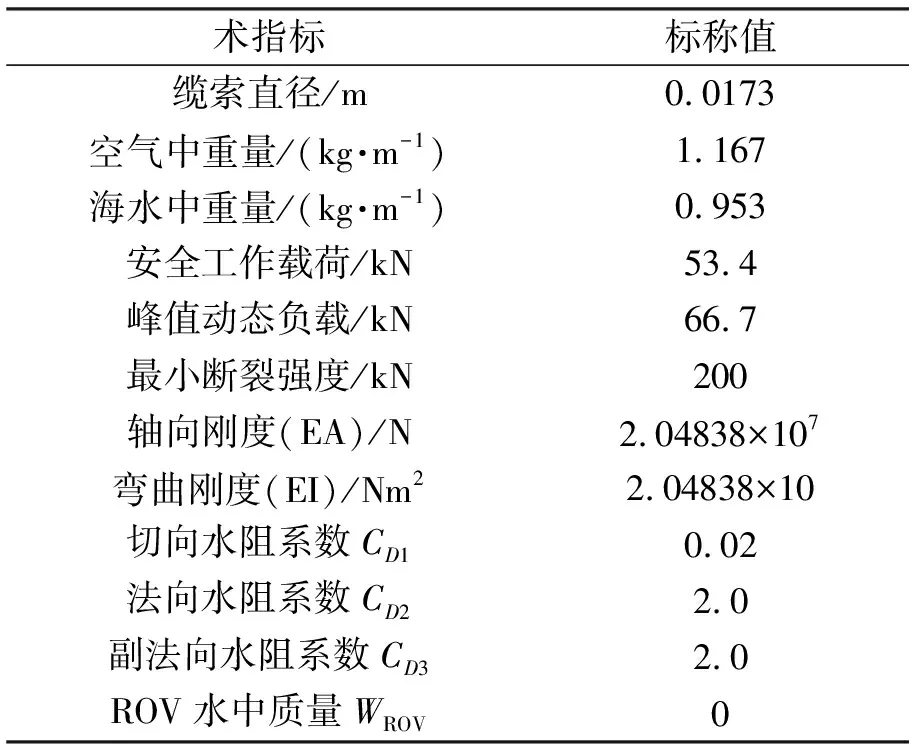
表1 “海星6000”ROV水下铠缆系统主要物理参数

影响水下铠缆系统安全工作的主要因素包括支持母船的升沉运动、铠缆自身参数变化以及海流流速变化。因此,在接下来的仿真中将综合考虑多个因素联合作用下铠缆系统的张力和运动规律变化。

4.1 未挂浮球仿真结果

首先采用广义α预测算法对“海星6000”ROV水下铠缆系统,在线性递减恒定海流和4级海况母船升沉运动共同作用下的动态特性进行分析。4级海况母船实测数据取自“大洋一号”科考船,数据包含母船升沉的位移、速度和加速度,采用频率为10 Hz,总时间长度为100 s,如图5所示,仿真中将该约束施加到铠缆首节点上。设海流只与深度相关,并且在全水深范围内是递减的,海水表面水平分量为0.8 m/s,竖直方向上无海流分量。仿真得到ROV下潜6 000 m深度时铠缆首端张力,以及80 s时刻水下铠缆空间动态构型分别如图6和图7所示。

图5 “大洋一号”母船升沉运动测量数据

由图6可知,铠缆首端张力值基本都超过了铠缆的安全工作载荷53.4 kN,铠缆首端张力在4.6～6.6 t范围内波动,均值为57.2 kN,若海况进一步提高,最大张力极易突破理论动态峰值负载66.7 kN,可能导致铠缆损坏失效。因此,为了提高铠缆的使用安全性,有必要采用一种抑制铠缆内部张力的方法。

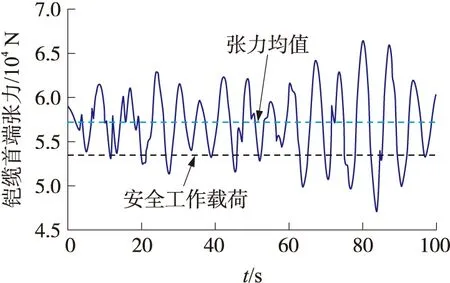
图6 “海星6000”ROV下潜6 000 m铠缆首端张力变化

由图7可知,ROV下潜深度6 000 m,在100 s有限时间内,由于海流的作用铠缆逐渐偏离初始直线状态,其偏离方向为海流的合速度方向,铠缆上半部分偏移量大于下端,由于仿真时间有限,最大偏移量并没有出现在铠缆的最末端,而是在深度约1 500 m位置。铠缆末端水平偏移量在80 s时为3 m(非铠缆稳态构型)。

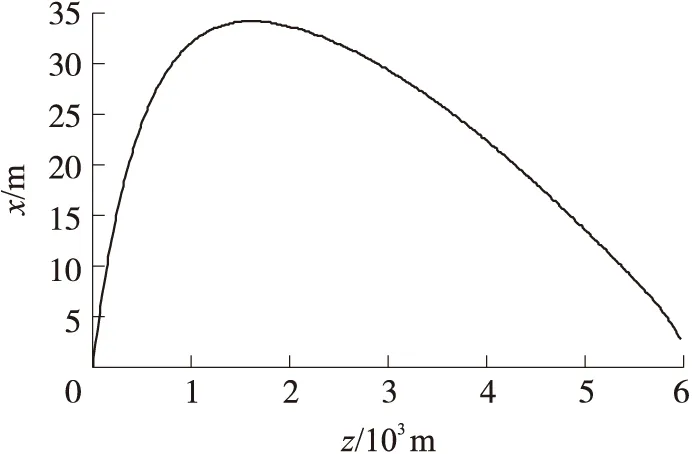
图7 80 s铠缆水下构型

4.2 铠缆局部系缚浮力球

由上节计算结果可知,ROV下潜到6 000 m级深度铠缆首端张力已超过安全工作载荷,极易导致其失效损坏,为了减少水面母船及铠装重缆对潜水器载体运动的干扰,同时降低铠缆内部张力值,本文拟在铠缆的某一段长度上系缚一定数量的浮球,所系浮球物理参数如表2所示,通过系缚正浮力球可抵消一部分缆索重量,从而起到降低铠缆内部张力的作用。每个浮力球由2个半球组成,中间留有走铠缆通道,通过卡子将缆夹在两半球间,浮球系在缆上场景见图8,与本文2.1节所建立的理论模型完全一致。浮力球在水下除了受到重力和浮力作用外,由于随缆一起运动,也会受到水动力及其附加质量力的影响,同时浮球对缆索微段也会有力的作用。因此,本文将浮球考虑为缆索外部节点,随缆一起运动,按照前文所建立的动力学模型进行数值仿真,首先证明系缚浮球是否能起到降低铠缆内部张力作用,仿真中在缆索的任意位置每隔2 m加挂浮球,分别加挂20、40和60个,仿真得到铠缆首端张力变化如图9所示。

图8 海试现场与铠缆系缚浮球场景

表2 浮球参数

图9 缆索系缚浮力球铠缆首端张力变化

由图9可知,在一定范围内,随着系缚浮力球数目的增加,铠缆首端张力波动均值逐渐减小;未加挂浮球时张力波动均值为57.2 kN,系缚60个浮力球后张力波动均值降低为53.4 kN。

由仿真结果可知,在铠缆上系缚浮力球确实可以降低铠缆内部张力,但具体在缆的那个位置系缚效果更佳,暂时还未知。通过查询相关文献发现,加拿大深海ROV系统ROPOS采用的是在近潜水器端系缚浮力球方式,如图10(a)所示,当铠缆绞车放缆50 m后,开始加系缚浮球,每隔2 m系缚一个,共系缚27个浮球;另外一种方案如图10(b)所示,绞车不断放缆,当水下铠缆重量接近缆安全工作载荷时,开始系缚浮力球,即远离潜水器端系缚浮球。两种方案铠缆首端张力波动如图10所示。

图10 缆索不同位置系缚浮力球方案

由图11(a)可知,当铠缆系缚10个浮球为时,两种系缚方案铠缆首端张力曲线基本吻合,由图11(b)可知,当铠缆系缚60个浮球为时,两种系缚方案铠缆首端张力曲线产生了明显差异,近绞车端系缚浮球张力曲线整体下移,两种方案张力均值分别为55 kN和54 kN,由此可见,在远离ROV端铠缆上系缚浮球效果更佳。通过上述分析最终确定采用远离ROV端系缚浮球方案;接下来要将确定系缚浮球的数量,即系缚多少个浮球才能保证ROV安全下潜到6 000 m级深度。

通过对“海星6000”ROV铠缆的物理参数分析可知,为确保安全下潜,最基本的要求是铠缆首端张力均值小于铠缆的安全工作载荷,为此本文进行了大量仿真,仿真结果如图12所示,由图可知,当系缚浮球60个时,铠缆首端张力均值为5.39 t,小于铠缆安全工作载荷;为确保铠缆的绝对安全,应使张力峰值小于安全工作载荷,通过数值计算得出,此时需要大约120个浮球,但这种方式过于保守,增加了潜器保障人员的工作量;综合考虑铠缆的安全性,同时满足ROV具有一定的作业半径(2 km),最终确定加挂系缚数量为90～100。

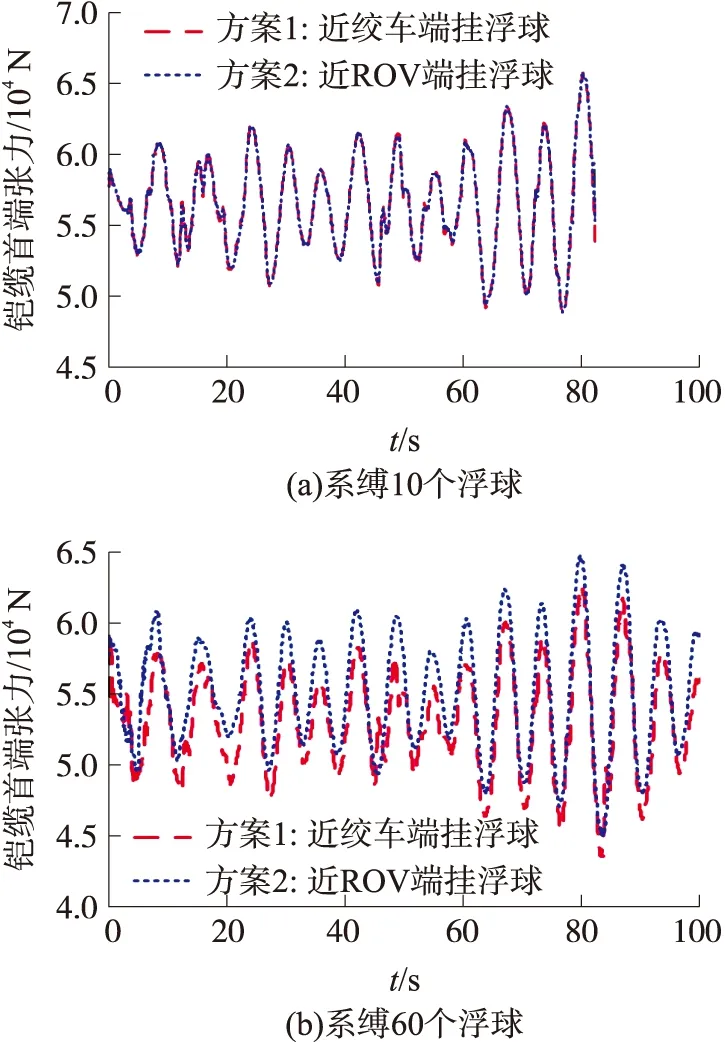
图11 两种方案铠缆首端张力对比

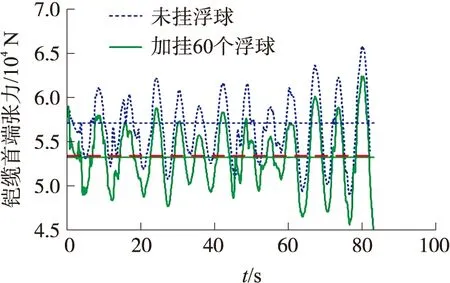
图12 铠缆系缚浮力球数量确定

为了解释两种加挂浮球方案差异产生机理,本文进行了大量仿真,仿真结果显示:当系缚浮球小于20个时,两者效果基本一致,当大于20个浮球时,首端张力差异逐渐产生,而20个浮球所提供的正浮力恰好与水下100 m铠缆重量一致;可见,当系缚浮球多于20个,近ROV端挂浮球铠缆会处于松弛状态,导致浮力无法完全作用到铠缆首端。由此可见,当浮球较少时,两方案无本质差异,当加挂浮球较多时,尽量选用远离ROV端加挂浮球。

5 海试验证

“海星6000ROV”于2015年初确定开展研制,2017年5月进行潜水器装配及联调,2017年9月完成水池和码头试验。在完成系统陆上联调、水池试验和码头试验的基础上,于2017年9月开展第一次海上试验验证。第一次海上试验的主要目的是通过由浅海试验至深海试验的过程,最终完成6 000 m深度级别的海上试验,全面考核潜水器功能、性能是否满足研制要求,为课题验收和ROV实际使用奠定基础,并视情况开展一定水下样品采集、原位要素测量、环境观测摄像等科学考察任务。

同时,为了验证本文理论计算结果的正确性,在6 000 m级潜次中,按照计算确定的最佳系缚浮力球位置和数量进行操作,海试现场及铠缆系缚浮球场景如图8所示,该潜次ROV最大下潜深度突破了5 611 m,试验得到铠缆首端张力和下潜深度曲线如图13所示。由图13可知,铠缆首端张力均值基本维持在50 kN左右,小于铠缆安全工作载荷53.4 kN,满足脐带缆安全使用要求,验证了本文理论计算的正确性。

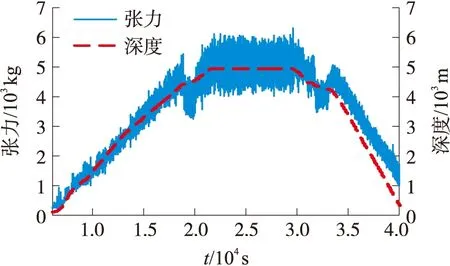
图13 系缚浮球后铠缆首端张力变化

6 结论

本文基于几何精确梁理论的有限元方法,建立了深海ROV水下铠缆系统的三维非线性动力学模型,基于该模型分析了在母船升沉和海流联合激励下脐带缆的动态特性,并提出了一种脐带缆内部张力抑制方法,最后通过“海星6000”海上试验验证了方法的有效性,结论如下。

(1)不采取任何措施的情况下,金属铠装脐带缆下潜到5 000 m级深度,铠缆首端张力就已波动超过脐带缆安全工作载荷,安全使用风险较高;

(2)通过在脐带缆上系缚浮球的方法,可有效降低铠缆内部张力值,当系缚浮球90～100个时,铠缆首端张力均小于安全工作载荷,满足安全使用要求;

(3)当系缚浮球较多时,尽量选用远离ROV端加挂浮球,张力抑制效果更为明显。