基于多能工配置的巡回式赛汝订单调度优化决策

张 哲,王丽丽,殷 勇

(1.南京理工大学 经济与管理学院,江苏 南京 210094;2.同志社大学商学院,日本 京都 602-8580)

赛汝(Seru)生产系统是一种灵活且反应灵敏的柔性制造系统[1]。它结合了Jobshop生产模式的高柔性、大规模生产模式的高效率以及高度可持续发展的环境友好性[2]。与传统装配线相比,在应对不确定的需求及动荡的市场变化方面更具竞争力[3]。Seru生产主要用于电子工业,大量用于组装生产[4]。因此,Seru属于小型的装配组织,通常只包括3个工序:装配、测试和包装[5]。一个Seru生产系统由一个或者多个Seru组成。每个Seru是一个小型紧凑的组装单元,由一些小型、简单和便宜的设备以及一个或多个致力于生产一种或多种产品的工人组成[3]。Seru生产单元具有完结性(Kanketsu)、工程间缔合性(Majime)和自律性(Jiritsu)的特点[6]。Seru有3种基本的类型:流程分割式Seru、巡回式Seru和单人货摊式Seru(屋台式Seru或Yatai)[7-10]。流程分割式Seru是传统流水线向Seru生产转变的第一种形式,整个生产过程是由几个经过交叉培训的工人合作完成的[4,10]。巡回式Seru是流程分割式Seru向单人货摊式过度的中间状态,这种形式的Seru生产单元工作台固定,每位工人都掌握着所有生产工序的操作,并且多能工一个紧跟一个绕着工作台循环作业,所以整个Seru的效率主要是由最慢的工作工人决定[4,8,10]。单人货摊式Seru是Seru进化的方向或者说高级形式,在一个Seru生产单元中只需要一个全能工,工人要掌握全部生产工序,以生产出所需产品[10]。实际上,这3种类型的Seru之间没有严格的优劣之分[1,11]。因此,对于企业而言,有必要根据其实际生产条件选择合适的Seru类型。本文研究的问题基于巡回式Seru,未来将考虑分割式Seru和单人货摊式Seru。

订单调度是制定订单生产计划的决策过程。它包括两个方面:一是将订单分配给可行的Seru,二是确定分配到各个Seru中的订单的生产顺序。其中,批量分割和换装时间是影响Seru调度的两个主要因素[4]。一方面,批量分割后的并行生产可以减少最大完工时间(Makespan)并增加整个系统的灵活性。另一方面,太小的批量则会导致频繁的换装,这可能会导致Makespan的增加。此外,在Seru生产方式下,经过交叉培训的多能工是实施Seru生产的基础和前提条件[12]。由于工人的技能组合及技能熟练水平的差异,工人和操作任务之间存在着多重匹配关系,不同的工人执行同一操作所需时间也有所不同[13]。因此,如何设计合理的多能工配置方案以充分发挥多能工的生产效率对优化整个Seru生产系统性能有着重要的影响作用。也就是说,工人分配的结果将会对订单的调度决策产生重要的影响。因此,该问题的研究对于解决Seru实际生产中的问题具有重大参考意义。目前,同时将这些问题进行研究的文章较少,且大多以最大化工人间的工作量平衡及最小化工人培训成本为目标[13,14],忽略了订单调度计划目标。Luo等[4]创新性地研究了带有工人分配的巡回式Seru调度问题,构建了一个双层规划模型,并设计了一种双层嵌套模拟退火遗传算法(SA-GA)进行求解。然而,该方法运算复杂而且运行时间较长。基于此,本文将多能工配置与Seru订单调度协同决策,设计了一种基于双层编码的改进型多目标混合遗传算法。

1 问题描述

假设现有一个巡回式Seru生产系统,在该生产系统存在W位拥有不同操作熟练度的多技能工人,且这些工人将会被分配给J个Seru生产单元用于I个订单的生产,这些订单包括P种产品类型。此外,各个工人对于各种类型产品的操作熟练度、每个订单的交货日期、需求量及产品类型、每种产品类型所需的换装时间及标准生产时间等参数是已知的。通常在接收到一系列的订单后,首先将由一线经理制定出工人-Seru分配计划。基于该工人分配计划,生产计划部门将会做出订单调度决策。实际上,工人分配结果与订单调度计划是相互作用、相互影响的。因此,制造商需要做出包括订单调度和工人分配联合决策。

在本文中,工人分配的目标是平衡每个Seru中工人的能力,即最大程度地减少工作人员的总闲置时间。在巡回式Seru中,工人负责单个产品的整个加工过程,但设备彼此共享。多能工一个紧跟一个从一个工作台移动到另一个工作台循环作业,以满足订单需求。因此,每个Seru的效率主要由该Seru中生产速度最慢的工人决定,并且该Seru中的其他工人将会停下来等待最慢的工人。因此,等待时间就是他们的空闲时间。Seru调度的目标是在计划期内保证所有的订单都能在交货期之前完工的基础上最大地减少整个生产系统的完工时间。且考虑批量分割以使生产计划更加地平衡和灵活。

2 模型建立

2.1 模型假设

(1)Seru的数目是给定的常数。

(2)每个订单只包含有一种产品类型;

(3)考虑批量分割,即一个订单可拆分成多个子订单并分配给不同的Seru;

(4)分配给某个Seru的订单或子订单所包含的全部的生产操作必须全部在该Seru内完成;

(5)Seru生产系统中的工人数量是恒定的,并且多技能工人的技能水平不会受到情感,身体和环境因素以及学习和遗忘的影响;

(6)考虑到布局紧凑,忽略了多技能工人在执行不同操作时在工作台之间移动的距离和时间;

(7)假设每个Seru中的第一个加工的订单的换装时间为零,且不考虑两个订单产品类型相同且连续生产的第二个订单的换装时间。

2.2 符号说明

(1)编号。i:订单编号,i=1,2,…,I;j:Seru编号,j=1,2,…,J;w:工人编号,w=1,2,…,W;p:产品类型编号,p=1,2,…,P;k:订单在Seru中的加工顺序,k=1,2,…,K。

Twp:工人w生产单件产品p所需时间。

(3)变量。

Qij:订单i分配给Seruj的量;tij:Seruj生产单件订单i所需产品的时间,其中,tij=max{w=1,2,…,W}{TwpZipfwjewp};STij:生产Qij所需的换装时间;

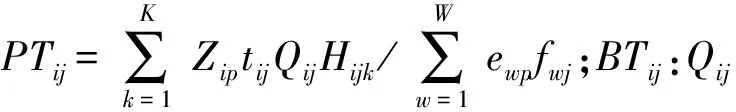
2.3 数学模型

minmakespan=

max{i∈{1,2,…,I}}{max{j=1,2,…,J}(CTij)}

(1)

minidle_time=

(2)

(3)

(4)

(5)

(6)

(7)

max{j=1,2,…,J}(CTij)≤Di

(8)

fwj,gij,Hijk∈{0,1}

Qij≥0,∀i,j

(9)

式(1)和式(2)是目标函数,分别表示Makespan和总的工人空闲时间;式(3)确保工人只能被分配给一个Seru;式(4)限制了一个Seru内的人数;式(5)确保订单只能分配到可行的Seru;式(6)表示订单需求量等于其子订单分配量的和;式(7)和式(8)保证了所有的订单均在交货期及Seru计划期前完成;式(9)表示变量Qij的非负逻辑约束。

3 改进型多目标混合遗传算法

第二代非支配排序遗传算法(Non-dominated sorting genetic algorithm II,NSGA-II)是有效求解多目标函数的算法之一,它降低了非劣排序遗传算法的复杂性,具有运行速度快和解集收敛性好的优点[15]。然而在处理高维问题时,NSGA-II容易陷入局部极值,出现早熟收敛现象[16]。模拟退火(Simulated annealing,SA)算法是一种基于蒙特卡罗迭代求解策略的自适应启发式概率搜索算法,具有简单性和强大的搜索功能的优点,但是缺乏对整体搜索方向的掌握。为了吸收这两种算法的优点,本文设计了一种有效的混合多目标优化策略—改进型多目标混合遗传算法来解决所提出的问题。

3.1 染色体编码

染色体的第一层包含W位基因,基因的值对应于Seru编号用来表示工人-Seru分配方案。染色体的第二层则表示订单调度结果。在进行订单调度前,将接收到的订单根据交货期从小到大排列并进行自然数编码,并通过实数编码以分配比率来表示订单调度方案。详细示例如图1所示。

图1 编码示例

3.2 解的检验与修正

染色体需保证个体能满足约束(3)～(9)。但是,在初始种群及由遗传操作产生的新个体中仍存在有很多不满足约束条件的非可行解。对于不满足约束(4)的个体,通过调整基因值来进行解的修正。对于不满足约束(6)的个体通过调节子订单的量来进行解的修正。修正方案如图2所示。对于不满足约束(5)、(7)及(8)的个体,则通过构造惩罚函数来抑制该类解的产生。

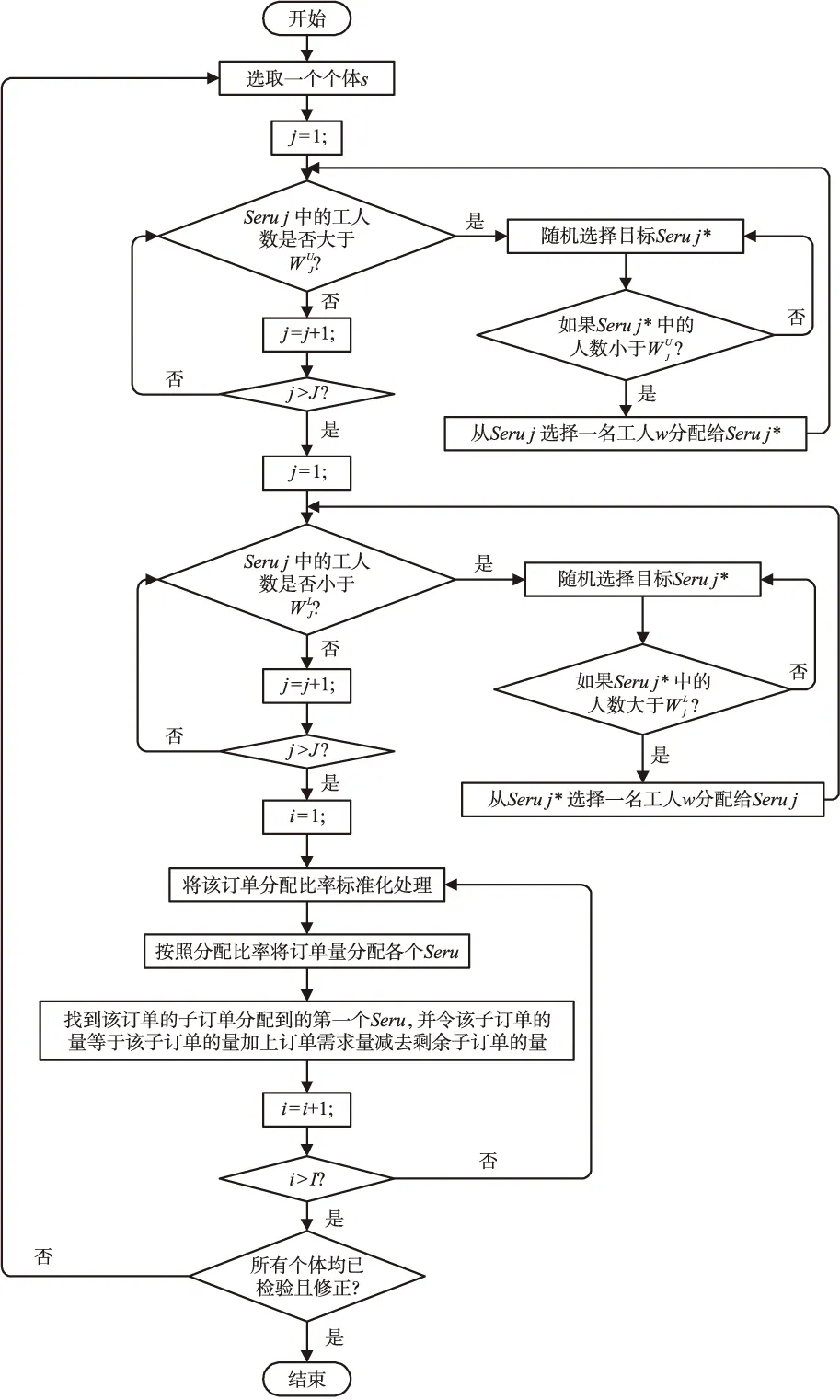
图2 可行性修正方案

3.3 遗传操作与模拟退火

首先通过非支配排序对种群中的个体进行分层,快速非支配排序的基本步骤如下。

首先令种群中的不被其他个体所支配的个体的rank=0;将这些个体储存到非支配前端F1中;然后将F1从种群中剔除,找出剩下的个体中不被其他任何个体所支配的解集,令其rank值为1,并将这些个体储存到非支配前端F2中,然后从现有种群中剔除F2,重复上述操作直到种群中的所有的个体都被分配到对应的非劣前端。

非支配排序完成后则需计算各层个体的拥挤距离。拥挤度是判断同一个rank层中个体的优劣的标准,拥挤度排序的目的是保持个体的多样性。个体的拥挤度是通过计算与其相邻两个个体在每个子目标值上距离差之和,其中边界解被指定为无穷大距离的值。本文希望同一rank层中的个体差异越大越好,所以对于同一rank中的个体拥挤度大的将被优先选择。

然后根据个体的rank值及拥挤度通过锦标赛选择选出父代个体。由于本文采用了扩展的双层染色体编码方法,因此染色体的上层需要分别进行交叉操作和变异操作。染色体上级采用单点交叉和单点突变。染色体下层采用矩阵单列交叉及矩阵单列变异操作。

种群经过交叉变异后,需执行SA操作,以两倍的Makespan与工人空闲时间之和作为适应度值,如果通过遗传操作生成的新种群中的个体具有较大的适应性值,则接受概率为1,否则根据等式(10)计算该个体的接受概率。

(10)

Tg+1=aTg

(11)

式中:p(Tg+1)为当温度为Tg+1时新个体的接受概率;fg+1为新个体的适应度值;fg为旧个体的适应度值;a为降火系数。

整个算法的流程如图3所示。

本文改进型多目标混合遗传算法参数值如表1所示。

表1 改进型多目标混合遗传算法参数设置

4 算例分析

引用Luo等[4]论文表2中的数据对所提出的基于双层编码的改进型多目标混合遗传算法进行验证。表2列出了该算例的非支配解集。表3和表4以解1为例给出了相应的工人分配方案以及订单调度计划。Luo等[4]以Makespan为主目标,工人空闲时间为次目标,采用SA-GA算法进行求解。由于Makespan占有主导地位,所以算法运行一次仅求得一个结果,不存在非支配解。这样并不是非常合理,企业面临不同的环境会有不同的侧重点。如企业较注重公平与员工满意度,可能会更加关注工人的生产任务均衡,而追求效率的企业则会更加关注Makespan。根据其文章中10次运行的结果得到了3个非支配解集如表6所示。

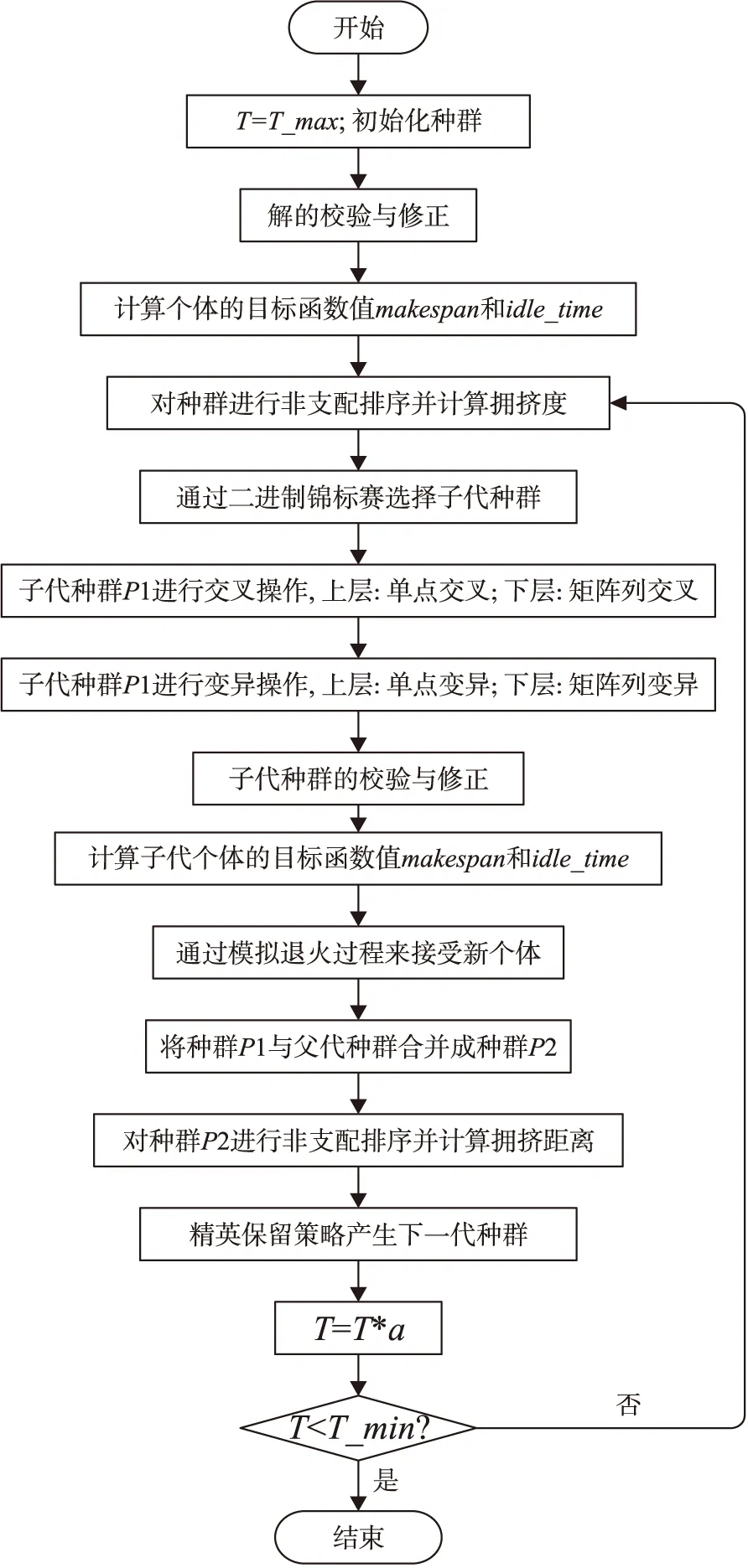
图3 算法流程图

图4直观地显示了两种算法的运行结果,可以发现本文所提出的算法在单独实现最小化Makespan及工人空闲时间方面更优,无明显的优劣之分。SA-GA算法单次平均运行时间约为8 156 s,而本文所提出算法运行时间约为160 s,运行时间缩短了约98%。为了验证所提出算法的可扩展性,本文引用了Luo等[4]论文中的大算例进行求解,表5列出了该大算例的非支配解集,表7是根据Luo等[4]论文中的5次运算得到的大算例的非支配解。通过比较发现本文所提出的算法在实现最小化Makespan方面较弱但差距极小,且在最小化工人空闲时间方面较优。另Luo等[4]论文中的算法在验证大算例时,其单次平均运行时间约为16 066 s,而本文算法仅需约490 s,详细比较如表8所示。

表2 非支配解集

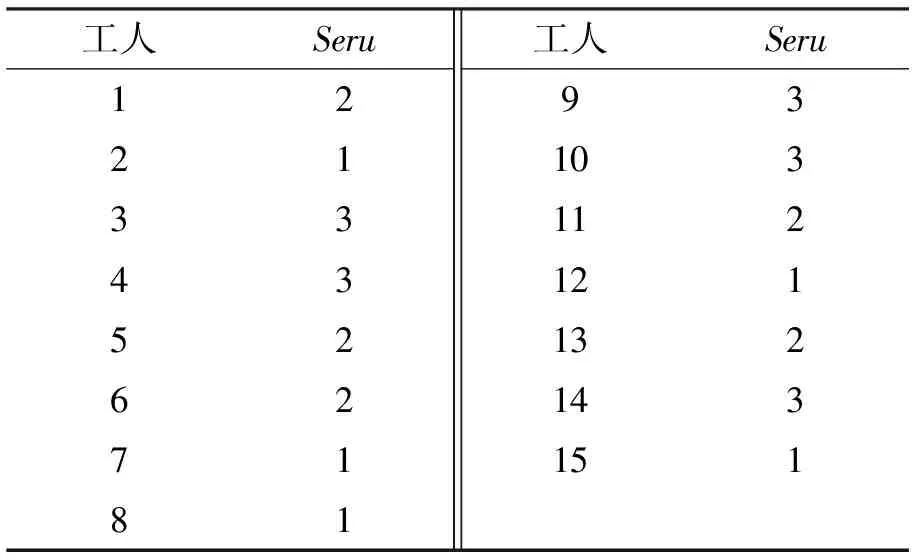
表3 解1对应的工人分配方案

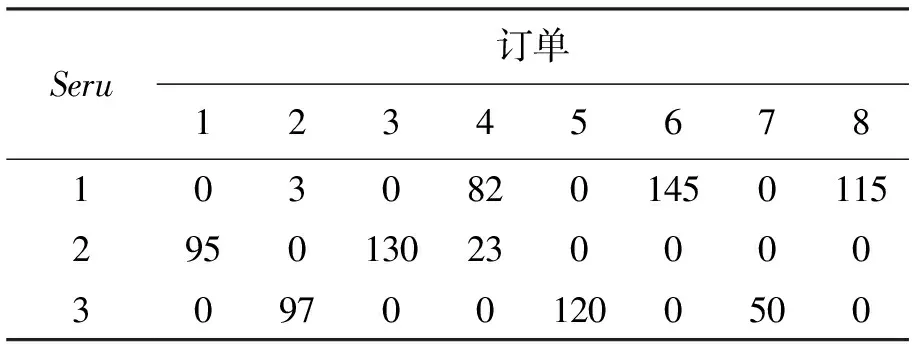
表4 解1对应的订单调度计划

表5 大算例非支配解集

表6 Luo等[4]文章小算例的非支配解集

表7 Luo等[4]文章大算例的非支配解集

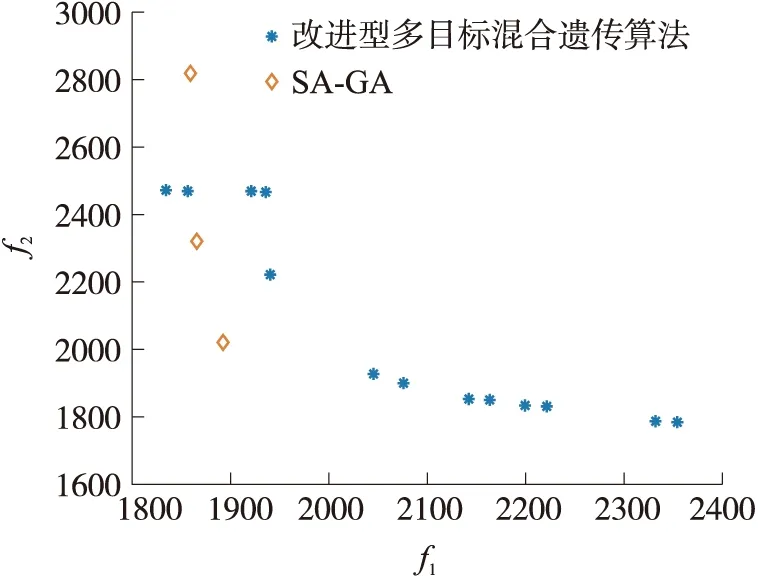
图4 两种算法的非支配解集

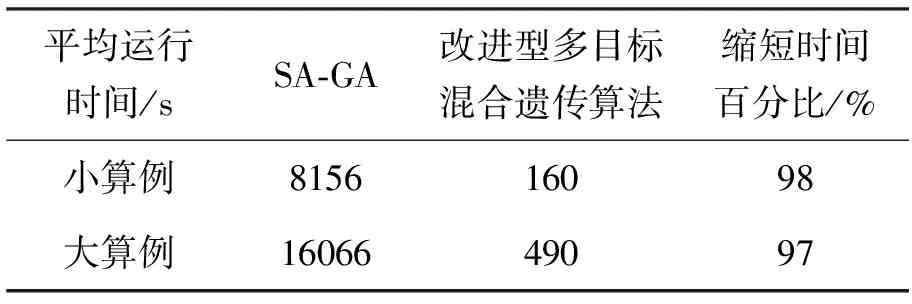
表8 算法运行时间比较

综上,本文所提出的多目标混合遗传算法相较与之前的研究,在求解小算例时,不仅能够获得较优的解,且算法运行时间大大减少(单次运行时间减少约98%);在求解大规模算例时,本文所求的解相较于之前的研究仍为非劣解,不仅如此,运行时间也缩短了约97%。实际上本文算法所优化的时间远不仅如此,先前的研究中所获得的非支配解集是经多次运算获得的。因此,其运行时间还需叠加。此外,大算例的数据相较于小规模算例增加了3倍多,而本文算法大算例的运行时间也约是小算例的3倍。因此,该算法的时间复杂度为线性时间。由此可证,文中所提出的基于双层编码的改进型多目标混合遗传算法是可行且有效的,并具有良好的可扩展性。

5 结论

本文研究了多能工配置与Seru订单调度协同优化决策,综合考虑工人分配、换装时间及批量分割等因素,建立了以最小化Makespan及最小化工人空闲时间为目标函数的多目标整数非线性规划模型。设计了一种基于双层编码的改进型多目标混合遗传算法对模型进行求解。数值算例结果表明,相较于SA-GA算法,本文所设计算法在执行大小算例所需的运行时间均缩短了98%,且目标函数值无优劣之分。本文算法在解决所提出的问题方面相较于之前的研究更加有效且具有良好的可扩展性。这对于解决Seru实际生产中的问题具有重大参考意义。

未来的研究还应考虑工人学习效应、遗忘效应、工人培训、员工离职以及其他影响工人技能水平的因素。此外,订单往往是在不同时间连续或随机到达的,并且可能还会取消订单,更改交货日期等,这直接影响到企业可以选择接受的订单集,也影响到订单调度决策。