弹药产品可靠度下限估计逐批迭代方法

缪云飞,王国平,贠来峰,2,战志波

(1.南京理工大学 能源与动力工程学院,江苏 南京 210094;2.江苏永丰机械有限责任公司,江苏 盱眙 211722;3.陆军南京军代局驻济南地区军代室,山东 济南 250031)

可靠性是评价武器系统整体性能的重要指标,对装备的战备完好性、任务成功率和寿命周期总费用等具有重要的影响。可靠度指标验证是在一定置信度下对装备的可靠度指标进行评估,以概率论和数理统计为理论基础,根据试验中获得的装备信息,应用统计学的理论进行推断,得出装备是否达到可靠度要求的一种统计试验方法[1-3]。现在可靠性评定方法较多,如经典法[4]、矩方法、贝叶斯法[5-10]、蒙特卡洛法[11]等。文献[12]采用折合信息的方法对系统可靠性进行了评估。贝叶斯方法综合采用先验信息和现场信息,对分析参数进行合理评估,获得了广泛应用。张士峰等[13]讨论了成败型产品可靠度的Bayes评估问题,通过引入继承因子,合理地考虑了产品的验前信息,进而把继承因子看作随机变量,得到了产品可靠度的验后密度函数。耿志强等[14]基于贝叶斯准则提出了一种基于总体平均经验模态分解残差进行故障诊断的新方法。翟胜等[15]针对传统可靠性分析方法在评估多态复杂系统时的局限性,提出了一种基于贝叶斯网络的多态系统可靠性分析方法。翟超等[16]基于贝叶斯信息融合理论,提出一种分层信息提取的多块主元分析故障监测方法。张聪等[17]提出了一种具有良好抗噪能力的贝叶斯可能性聚类模型。李婧等[18]应用贝叶斯方法建立一种对装备中指数型单元贮存寿命分布参数的估计方法。王新鹏等[19]建立基于传统贝叶斯网络和考虑共因失效的贝叶斯网络的鱼雷系统可靠性评估模型。宋一凡等[20]在缺乏足够先验试验数据的情况下,运用Bayes方法,综合专家经验和模糊评判推理进行故障检测,弥补了传统可靠性分析方法的不足,提高了可靠性分析的准确性。贠来峰等[21]提出了某型子母弹靶场交验试验方法从安全性、可靠性和一致性3个方面设置试验项目的设想。本文针对弹药类产品逐批交验的工程背景,基于Bayes理论的思想,提出了一种可靠度下限估计的逐批迭代算法。

本文研究的问题可以简要表述为:在可靠性计数型抽样检验实施过程中,已知某批产品在置信度v条件下的可靠度下限验前估计值为RL,0,本批的试验结果为(n,F),n为试验发数,F为失效数,求验后的可靠度下限估计值RL,1。基本方法是利用二项分布来估计弹药产品的可靠度。基本思路是把验前信息转化为对应于失效数为1的试验样本量,再通过引入继承因子把验前信息与本批试验结果融合为一个等效试验结果,然后由等效试验结果计算出验后的可靠度下限估计值。

1 基于失效数的可靠度下限估计算法

对于成败型试验,工程中可以通过计数数据来估计弹药产品的可靠度。计数数据估计可靠度的方法一般使用二项分布和超几何分布两种。假设统计可靠度试验中试验数为n、失效数为F以及总批量为N。前者适用于大批量小样本抽样的可靠度下限估计,一般当批量N≥10n时适用;后者适用于小批量大样本抽样的可靠度,通常当批量N<10n时适用。在Bayes小子样抽样检验中满足N≥10n,因此本文通过二项分布估计可靠度。在置信度水平ν下,可靠度R可由式(1)求出。

(1a)

1-νF≥0

(1b)

式中:n为试验发数,ν为置信度水平,R为可靠度下限,以下用RL表示。

当F=1时,式(1b)可表达为

(1-n)Rn+nRn-1=1-ν

(2)

例如,对某炮弹试验n=20发,仅失效F=1发,指定置信度水平为v=0.90,则由式(2)可求解出其可靠度下限达到了RL=0.818 9。

再例如,若某炮弹在某交验试验前已进行了多次试验,统计试验表明在置信度水平v=0.90条件下,可靠度下限达到了RL=0.95,则可由式(1)将这一经验信息转化为一个具体的试验结果。若假设这个试验结果中有F=0发失效,则可由式(1a)求解出试验次数n=45。若假设这个试验结果中有F=1发失效,则可由式(2)求解出试验次数n=77。若假设这个试验结果中有F=2发失效,根据相应的失效数公式可求解出试验次数n=105。

2 可靠度验前估计的逐批迭代算法

问题表述如下:

(1)指定置信度水平v:对炮弹产品通常取v=0.90;

(2)已知验前信息:可靠度下限RL,0;

(3)已知本批试验结果:(n1,F1),n1为试验次数,F1为失效发数;

(4)求验后可靠度下限估计值:RL,1=f(n,F,v);

基于Bayes思想,引入继承因子,将把验前信息与本批试验结果融合为一个等效试验结果:

n0=f′(F0=1,RL,0,v)

(3)

n=md+n0×C+n1

(4)

F=F1+1

(5)

式中:n为等效融合样本量,F为等效融合失效数,F1为本批试验的失败数,n0为本批产品可靠度下限估计值验前信息对应的平均失效数F0=1时的等效样本量,C为继承因子,n1为本批的试验样本量,md为与固有质量特性有关的等效样本量。

md由设计定型试验结果决定,对应于失效数为0的试验样本量。假设某产品设计定型试验结果为(30,0),则md=30。若试验结果为(30,3),第一步先求出对应的可靠度下限值为RL=0.790 7,第二步求出该可靠度下限值对应失效数为0的样本量md=10。

3 继承因子的确定

3.1 理论分析

假设对某炮弹产品进行了1 000发试验,试验结果为(1 000,0),即0发失效数,由式(1)可计算出在v=0.90时,RL=0.997 7。现将这1 000发试验分为10组,每组100发,0发失效数,以C为0.6、0.7、0.8和0.9,分别由式(1)可计算出每次试验后的RL,可靠度下限逐批迭代的计算结果如图1所示。若不考虑验前信息,仅从试验结果(100,0),可得可靠度下限RL=0.977 2,而在考虑了验前信息(第一次试验以设计定型试验结果(30,0)为验前信息)的基础上,第一次试验结果的可靠度下限估计值分别为0.976 0(C=0.6)、0.976 8(C=0.7)、0.977 4(C=0.8)、0.978 1(C=0.9)。可以看出,当继承因子偏低时,验前信息占的比重过小,对结果的影响也比较小,导致逐批迭代的结果与实际的RL相比差距太大。当继承因子为0.8和0.9时比较符合实际结果。

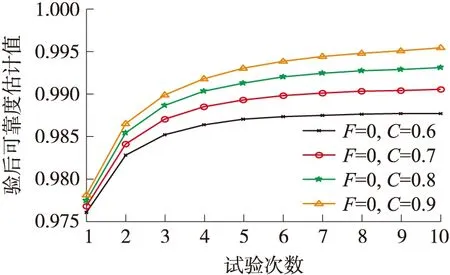
图1 试验结果为(100,0)时,可靠度下限迭代结果

在上述条件不变情况下,试验结果为(1 000,10),即10发失效数,由式(1)可计算出在v=0.90时,RL=0.983 1。将这1 000发试验分为10组,每组100发,1发失效数,计算出在不同继承因子下的验后RL,可靠度迭代计算结果如图2所示。若不考虑验前信息,仅从试验结果(100,1),可得可靠度下限RL=0.961 6,而在考虑了验前信息的基础上,不同继承因子的第一次试验结果的可靠度下限估计值均大于不考虑验前信息的估计值。与实际可靠度下限值0.983 1相比,当继承因子偏低时,可靠度下限估计水平明显偏低,而当继承因子为0.9时明显偏高。在继承因子等于0.8时最为适宜,可靠度下限迭代结果为0.982 8。

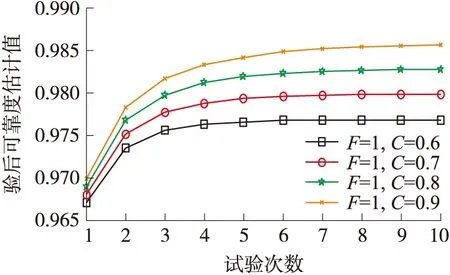
图2 试验结果为(100,1)时,可靠度下限迭代结果

3.2 经验观测

假设某炮弹设计定型试验结果为(30,0),则md=30,可靠度下限为0.926,连续交验10批,每批的试验结果均为(5,0),分别取C=0.6、0.7、0.8、0.9,计算结果如图3所示。在未进行试验之前可靠度下限为0.926,随着批次的增加,可靠度下限估计值逐渐增大并趋于稳定水平。当继承因子偏低时,达到的稳定水平也较低。

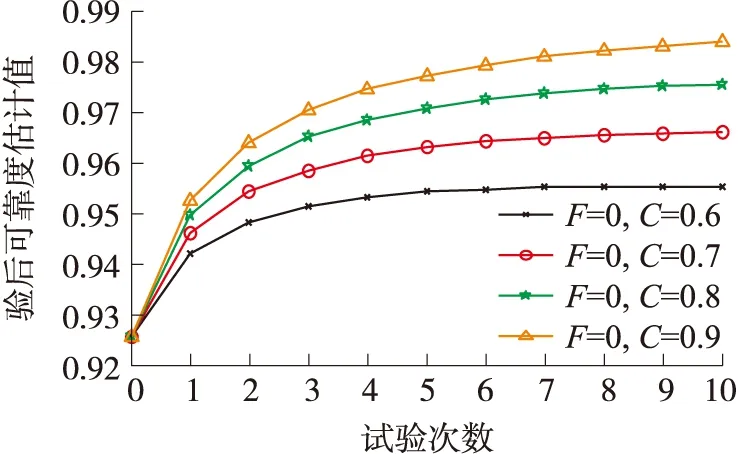
图3 试验结果为(5,0)时可靠度下限迭代结果

在上述条件不变下,每次试验结果均为(10,0)时,可靠度下限估计值逐批迭代结果如图4所示。可以看出当试验样本量增大时,可靠度下限估计值也会增大,与经验值0.977相比,继承因子为0.8时较为适宜。图5为试验结果(10,0)和(20,1)交替迭代时,可靠度下限估计值计算结果。可见,可靠度下限估计值整体呈上升趋势,并随着批次的增加趋于稳定。当试验结果较差时,可靠度下限估计值会略微减小,因此本文提出的可靠度逐批迭代算法能够较好地反映试验结果。最后,结合弹药靶场工作人员的经验和协商,取继承因子为0.8较为适宜。

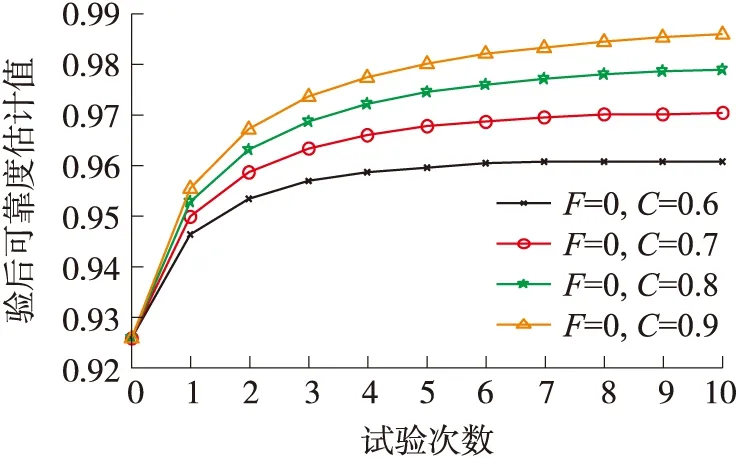
图4 试验结果为(10,0)时可靠度下限计算结果

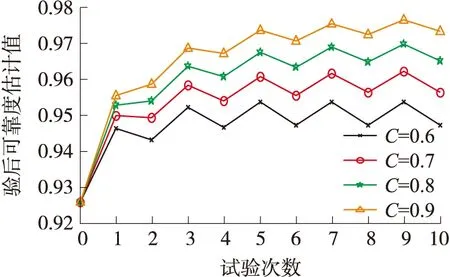
图5 试验结果为(10,0)和(20,1)交替进行时可靠度下限估计值迭代结果

4 影响因素分析

根据理论分析可知,影响可靠度下限估计值的因素为试验样本量、试验的失效数和固有质量水平。分析过程中继承因子取0.8,连续交验10批。

4.1 试验样本量

假设某炮弹设计定型试验结果为(30,0),每批的试验结果分别为(5,0)、(10,0)和(15,0)时,可靠度下限估计值计算结果如图6所示。

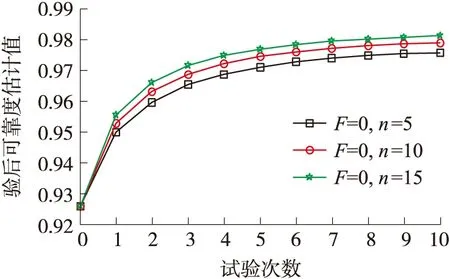
图6 试验样本量对可靠度下限估计的影响

可以发现失效数一定时,相同样本量下验后可靠度下限估计值都是随批次的增加而增大并且趋于稳定值,说明本文提出的可靠度逐批迭代算法是合理可行的。当试验样本量越大时,可靠度下限估计值越大。这是因为,当试验样本量越大时,等效融合样本量也就越大,导致本批的可靠度下限估计值就比较大。

4.2 试验失效数

假设某炮弹设计定型试验结果为(30,0),每批的试验结果分别为(10,0)、(10,1)和(10,2)时,可靠度下限估计值计算结果如图7所示。可以发现在不同的失效数下,可靠度下限估计值都逐渐收敛于稳定的水平。当失效数越小即产品的试验结果越好时,可靠度下限估计值越大,这是因为在等效融合样本量相同的条件下,失效数越多,可靠度越差。

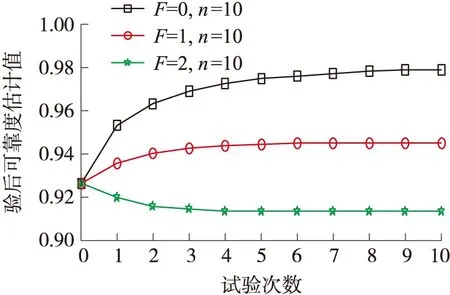
图7 试验失效数对可靠度下限估计的影响

4.3 固有质量水平

假设某炮弹设计定型试验结果分别为(30,0)、(30,1)和(30,2),每批的试验结果为(10,0),可靠度下限估计值计算结果如图8所示。由定型试验结果转化为可靠度下限值分别为0.926 1、0.876 3和0.832 2,当固有质量水平越高时,可靠度下限估计值越大。这是因为,固有质量水平越高,转化的等效样本量就越大,等效融合样本量就越大,导致可靠度下限估计值越大。但是,随着批次的增加,试验样本量增多,可靠度下限估计值逐渐趋于稳定水平,固有质量水平对可靠度下限估计值的影响越小。

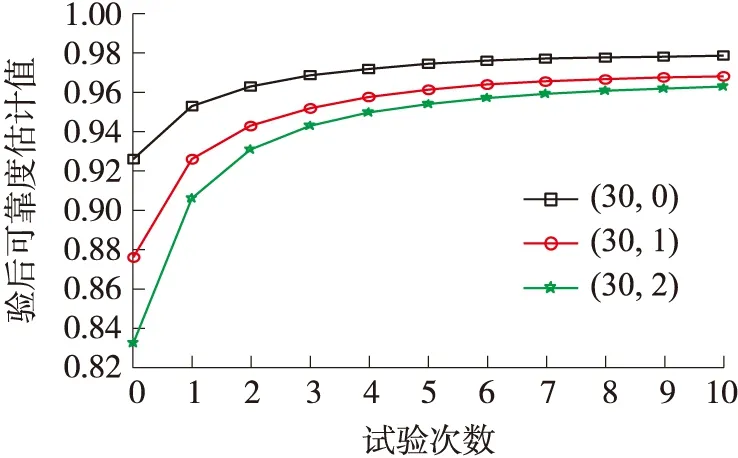
图8 固有质量水平对可靠度下限估计的影响

综上所述,对比继承因子相同,连续交验10批之后的可靠度下限估计值,可见,(1)当定型试验结果相同时,可靠度随每批试验发数的增加而略微增加,但是随着失效数的增加而大幅减少;(2)固有质量水平影响初始的可靠度值,当交验每批试验发数和失效数不变时,可靠度下限估计值变化不大。因此,试验的失效数对可靠度下限估计值的影响权值更大。

5 算例

例1 某型号炮弹产品,设计要求可靠性指标的置信度为0.9,R≥0.9。到鉴定试验阶段,收集的先验信息为定型试验数据(38,1)。验收试验时,连续交验20次,每次试验结果分别为(5,0)、(10,1),可靠度迭代计算结果如图9所示。

图9 某炮弹可靠度下限估计逐批迭代结果

例2 某型号导弹产品置信度为0.7,设计定型时可靠度水平为0.9,连续进行20次试验,每次试验分别为(4,0)、(6,1),可靠度迭代计算结果如图10所示。

图10 某导弹可靠度下限估计逐批迭代结果

6 结论

本文针对抽样检验中可靠度下限估计问题,提出了一种基于失效数的可靠度逐批迭代算法。通过引入继承因子把验前信息与本批试验结果融合为一个等效试验结果,然后计算出验后的可靠度下限估计值。通过理论分析和经验观测确定了继承因子的大小,并对影响可靠度下限估计值的试验样本量、试验失效数和固有质量水平等因素进行了分析。最后应用该方法对某炮弹和导弹进行了可靠度下限估计计算,计算结果表明本文提出的可靠度逐批迭代算法是合理可行的。下一步工作将对本文的迭代算法进行试验验证。