大攻角失速下翼型非线性颤振速度计算分析
展志焕,顾超杰,胡盛靖,陈东阳
(1.北京机电工程研究所,北京 430064;2.扬州大学 电气与能源动力工程学院,江苏 扬州 225127)
国内的许多学者进行了考虑结构非线性的颤振问题研究[1]。杨智春等通过使用等效线性化理论,分析了初始间隙参数、速度参数等参数对具有非线性特性的二元翼型颤振的影响[2]。郑国勇等对不可压缩流中机翼外挂系统的分叉问题进行了研究[3]。对于气动力的非线性,赵永辉等采用ONERA气动力模型对三维弯扭耦合梁进行了大攻角下的颤振分析[1,4,5]。张健等采用非线性梁理论和ONERA气动模型,对在侧向随动力作用下的大展弦比机翼的气动弹性稳定性进行了研究[6]。
航天航空领域和船舶与海洋工程领域中,失速问题对飞行器的机翼、水下航行器的控制舵和高速船舶的水翼等舵面结构的设计和使用产生重大的影响。尤其在失速状态下,机翼、舵叶可能发生非线性颤振,进而会导致机翼、舵叶结构发生持续的振动,诱发结构疲劳损伤。因而,对于失速下的颤振分析是十分必要的。通过对翼型颤振进行时域分析,可以有效预测翼型颤振速度,并且直观展现气动弹性响应。
对于建立在非定常力气动模型基础上的气动弹性问题的研究是于20世纪的六七十年代开始的。在工程应用实际问题的需要下,专家学者在早年时期对非定常气动力和气动弹性分析应用做了大量的计算研究[7-10]。郭曼丽等[11,12]使用最小二乘无网格算法实现了翼型的流场数值模拟。二元颤振模型一般用于气动弹性的原理分析和验证。沿展向的所有剖面的翼型都是相同的,并假定绝对刚硬。叶片的弯曲和扭转变形分别用二元水翼的沉浮和俯仰运动来模拟[13,14]。这种典型截面通常应用于大展弦比平直机翼,也可以用于气动力控制面的建模。传统线性颤振计算方法不能准确解决非线性系统的气动弹性问题。采用两自由度二元翼型任意运动时域气动力方法计算叶片非线性气动弹性问题,这种方法易于工程实现,为叶片非线性气动弹性分析研究提供了一种有效的计算分析途径。
ONERA气动力模型是一个非定常、非线性、半经验的气动力计算模型。该气动力模型是在二维翼型经风洞试验获得的实验数据的基础上,经过拟合得到的一种半经验的模型,可应用于大攻角的情况[1]。本文采用ONERA失速气动力模型,建立二元翼型非线性颤振动力学模型,分析了不同结构参数对大攻角二元翼型非线性气动弹性的影响。
1 ONERA失速气动力模型
ONERA气动模型利用小幅度振动试验数据来预估失速振动时受到的气动力,并且模型中的线性部分模拟了Theodorsen气动力,非线性部分对静态失速影响进行了考虑。ONERA气动力模型,其表达式在各个文献中各不相同,本文选用的气动力模型表达式如下[1]
(1)
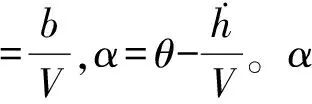
因为ONERA气动模型可以看成线性和非线性两部分,线性部分又表示对Theodorsen气动力的模拟。所以,根据两部分关系,表1给出了线性部分的相关参数值。

表1 ONERA气动模型线性部分相关参数值
非线性部分是对静态失速的影响的考虑,其中相关的参数值为
(2)
(3)

r3L=r3M
(4)
式中:ΔCz为静态空气动力系数曲线的线性延长部分与非线性部分的差,可见图1中的展示,同时表示为
ΔCz(α)=αozα-Cz(α)
(5)

图1 静态气动力曲线[1]
通常,为了简化计算,将静态气动力曲线用其折线相似代替,如图2所示,所以ΔCz可以写为
(6)
(7)
(8)
(9)
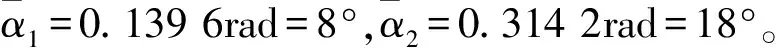
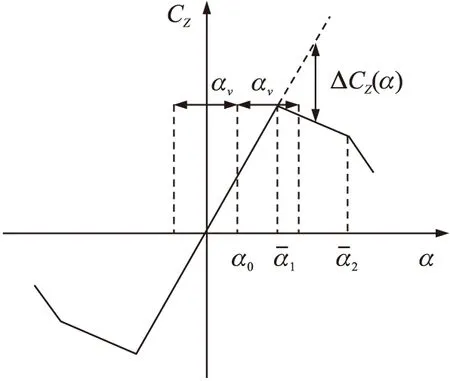
图2 静态气动力曲线的折线相似[1]
ΔCz对α的偏导数为
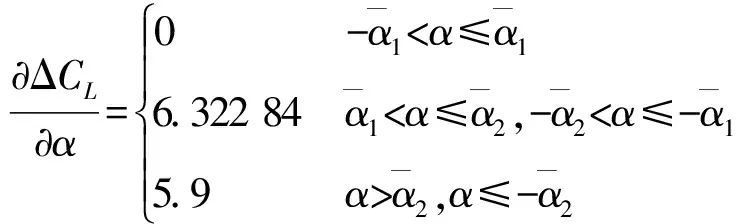
(10)
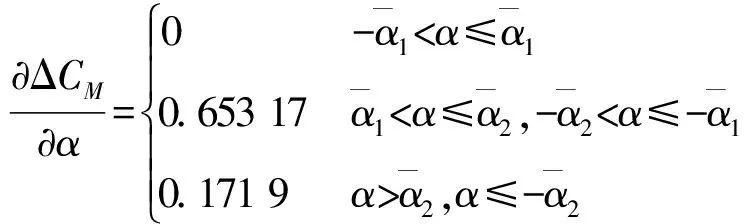
(11)
2 二元翼型非线性气动弹性模型
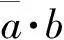
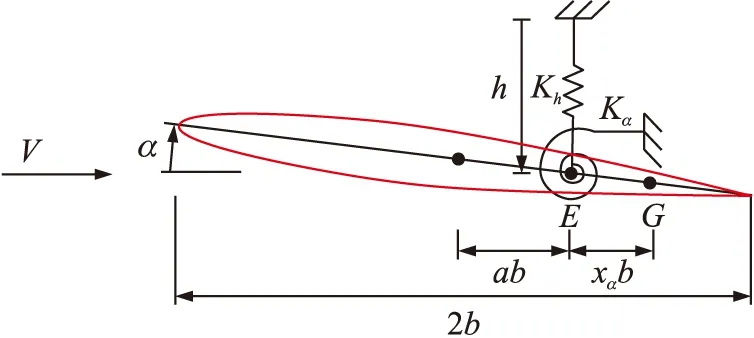
图3 二元翼型结构模型[1]
对上述的二元机翼结构模型可以推导出气弹方程
(12)

结合ONERA气动力模型对气弹方程建立状态方程

(13)
式中:
对方程(13)利用Runge-Kutta法进行求解,可以获得非线性气动弹性响应。计算时间步长为0.001 s,初始沉浮速度为0 m/s,初始俯仰速度为0.01 rad/s。
3 结果分析
表2为ONERA气动模型仿真所用物理参数。

表2 仿真参数
分别对来流速度为600 m/s、900 m/s两种工况进行仿真,计算结果如图4、5所示。
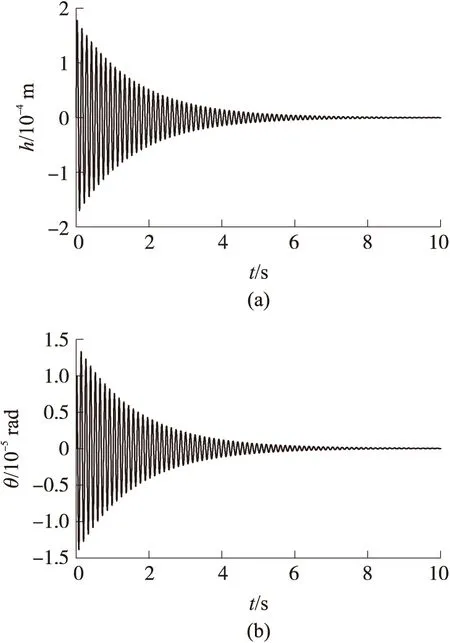
图4 v=600 m/s响应曲线
可以发现当来流速度为600 m/s时,二元翼型俯仰和弯曲运动都随时间减小,即趋于收敛;当来流速度为900 m/s时,翼型振动逐渐增大,即趋于发散。通过二分法在600 m/s和900 m/s范围内搜索非线性颤振临界速度。通过仿真计算可以确定,在该组参数的情况下,非线性颤振速度为811 m/s。计算出的振动响应曲线如图6所示,翼型俯仰和弯曲运动保持稳定。

图5 v=900 m/s响应曲线
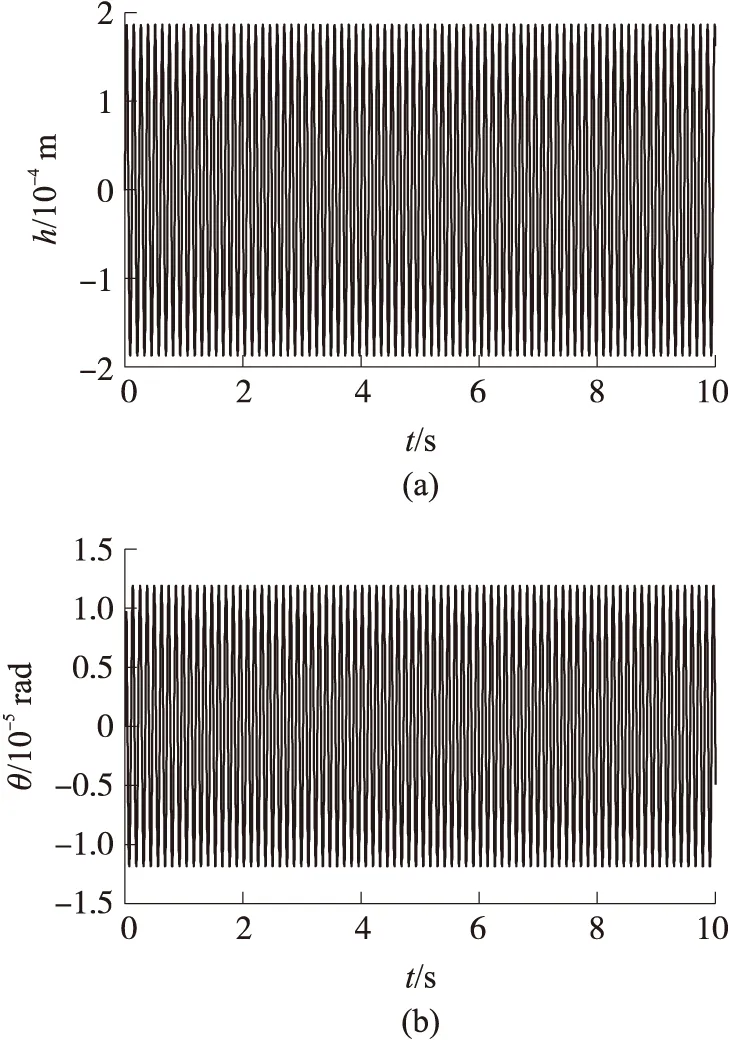
图6 v=811 m/s响应曲线
采用同样的方法,研究半弦长的变化对该组参数情况下翼型非线性颤振的影响规律,其他参数保持不变。如图7所示为不同半弦长下计算出的翼型颤振临界速度。图中显示随着半弦长b的值增大到0.4处,颤振临界速度会发生明显的阶跃。当b=0.5 m时,该组参数情况下,非线性颤振临界速度达到一个极大值。b继续增大,颤振临界速度趋于800 m/s。这表明翼型的弦长设计有一个最佳的点,在该点下翼型的颤振临界速度达到最大,即翼型发生颤振的难度增大。同时在较大的半弦长下,翼型的颤振临界速度变化不大。
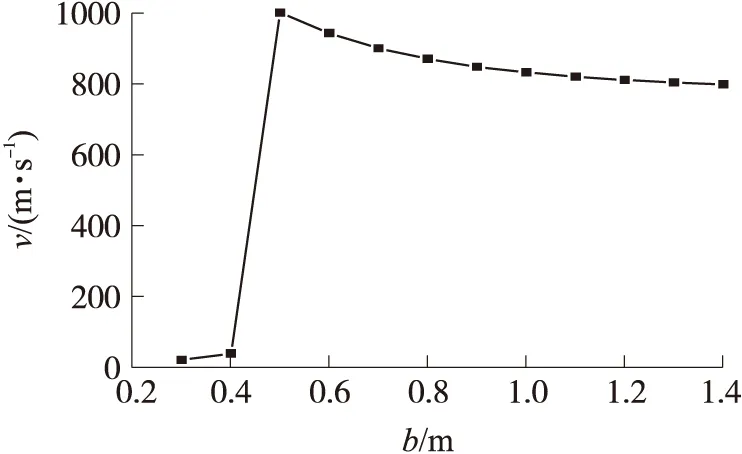
图7 颤振速度随半弦长变化图
4 结论
本文基于ONERA失速气动模型,利用二分法,对某特定参数下大攻角失速翼型的非线性气动弹性进行了仿真,确定在ONERA气动失速模型下的翼型颤振临界速度。同时,通过仿真预测了半弦长对失速翼型气动弹性的影响规律,计算发现,半弦长的值变大,颤振速度会发生突跃,在某一个点,颤振速度存在极值点。颤振速度越大,发生颤振的难度越大。因此通过本文的方法可以预测不同的结构参数对失速翼型颤振速度的影响,合理地设计翼型结构。

