基于网络局部和全局特性的组合中心性度量措施

卢鹏丽, 周 庚

(兰州理工大学 计算机与通信学院, 甘肃 兰州 730050)

近年来,复杂网络的研究在航空线路[1]、电网[2]、社交网络[3]、生物网络[4]和生态网络[5-6]等领域受到了广泛的关注.网络的无标度特性[7]和小世界特性[8]使得网络中的一些重要节点对网络的结构和功能有着很大的影响.当这些节点在网络中出现故障时,它们的影响将迅速扩散到整个网络.因此,如何准确量化复杂网络中节点的重要性,找出关键节点,具有重要的理论和现实意义[9].例如:控制疾病网络中的关键节点能有效防止病毒的大规模传播[10]；在社交网络中控制关键节点将有助于阻止谣言的扩散[11]；准确找到电力网络的重要节点,对其加以重点监管和保护,可使得电力传输顺利进行,有效防止大面积停电事故的发生[12]；识别和控制交通网络中的重要节点能有效解决交通拥堵的问题.

针对复杂网络中节点重要性的评价,学者们提出了度中心性(DC)[14]、接近中心性(CC)[15]、介数中心性(BC)[16]、特征向量中心性(EC)[17]、子图中心性(SC)[18]、谱密度中心性[19]和K-core中心性(KC)[20]等方法.虽然已有的中心性准则得到了广泛的应用,但也存在不足.度中心性易于计算,但它只考虑局部信息,忽略了网络的全局结构.紧密性中心性考虑的是节点间最短路径的平均长度,但在处理具有大量孤立节点的网络时会失败.介数中心性是通过计算经过某一节点的最短路径的个数来衡量节点的重要程度,但是如果有很多节点不属于其他节点对的最短路径时,则其计算值为0[21].许多学者尝试从不同的角度去寻找评价节点重要性的方法,但是对于一个实际的网络来说,用单一的指标来描述节点的重要性是片面的[22].学者们在实验的过程中发现同一网络在不同的中心性准则下,节点的重要性排序结果可能不同,如何更精确地识别节点重要性仍然需要进一步研究.本文结合逆和指数(ISI)[23]、度中心性(DC)和介数中心性(BC),通过给三种指标设置权重(即放缩参数),定义了新的中心性指标IDB.新的中心性指标从节点自身、邻居和全局三方面考虑节点的中心性,相较于单一节点中心性指标,新指标考虑得更全面、更精确.

目前,节点重要性仿真实验主要有静态攻击和动态攻击两种方式[24].静态攻击只考虑网络的初始信息,可是随着节点的移除,网络的结构会发生变化,因此节点的重要性也将与初始值不同,如果还是依照网络初始的节点重要性顺序移除节点,攻击效果将不能够达到最佳.为了保证每次移除的节点是当前网络中最重要的节点,每次移除一定比例的节点之后都要对当前网络中的节点进行重新排序再进行删除,重复此过程直到所有的节点被移除,这种攻击方式被称为动态攻击.在攻击效率上,动态攻击一般优于静态攻击,但是攻击代价(即运算时间)也远高于静态攻击.本文中只采用动态攻击方式进行仿真实验.

本文在两种人工网络和两种实际网络[25]上进行实验.实验中,以网络的最大连通子图的相对大小作为评价标准[26],根据五种中心性指标BC、DC、KC、ISI、IDB对网络中的节点进行重要性排序,利用动态攻击的方式每次移除20个节点,重复上述操作,直到将网络中所有节点删除(当网络剩余节点不足20时,仍需要进行一次删除操作).然后对比移除过程中4种网络模型的最大连通子图的相对大小的变化情况来反映四种指标的攻击效果.实验结果表明,与单一中心性准则相比,组合中心性指标IDB能够得到更准确、更全面的结果.

1 相关研究和本文算法

1.1 传统中心性指标

传统的节点中心性问题主要分为基于邻居信息的节点中心性研究、基于经过节点最短路径数目的节点中心性研究和基于节点移除以及收缩的节点中心性研究[27-28].基于邻接信息节点中心性研究主要关注的是网络节点本身的信息及其邻居节点的信息；基于经过节点的最短路径数目的节点中心性研究主要是考虑信息流在网络中的传播；基于节点的移除和收缩的节点中心性研究侧重于研究节点删除和收缩过程中网络拓扑结构发生的变化.本文根据逆和指数、度中心性和介数中心性,结合放缩参数法,提出了新的组合中心性指标,即用IDB来识别网络中的关键节点.设网络G=(V,E),其中V={v1,v2,…,vN}为其节点集,E={e1,e2,…,eL}为其边集,节点数为N,边数为L,di为节点vi的度.

1) 度中心性.复杂网络中节点的度中心性表示的是一个节点邻居的个数占总节点数的比例,最直观地认为邻居越多,节点就越重要.复杂网络中节点的度中心性定义为

(1)

2) 介数中心性.节点的介数中心性是指网络中经过该节点的最短路径的数目占该网络中最短路径总数的比例.节点v的介数中心性定义为

(2)

其中:δst(v)表示网络中从任意节点s到节点t且经过节点v的最短路径的条数;δs表示网络中从任意节点s到节点t的最短路径的条数.

3) K-core中心性.节点的K-core中心性是根据节点的位置度量节点影响力.K-core分解算法通过迭代删除节点,给网络中所有节点赋予K-core值.算法思想如下：首先,从图中删除所有度为1的节点以及相关的连边,若剩下的节点里仍有度值为1的节点,则重复上述操作,直到图中所有节点的度值都大于1,并且将所有删除的节点的K-core值记为1，即这些节点均处于K-core值为1的层.然后删除度为2的节点,直到没有度为2的节点，将所有删除的节点的K-core值记为2,这个过程一直持续到所有节点都删除为止,即每个节点独有对应的K-core值.显然,K-core值越大的节点越接近网络的中心位置,节点影响力也就越大.

1.2 组合中心性指标IDB

节点的逆和指数表示的是节点自身的度与其一阶邻居节点的度之间的关系,图中任意节点u的逆和指数定义为

(3)

IDB(v)=alog(ISI(v))+blog(DC(v))+

clog(BC(v))

(4)

2 网络数据和评价标准

2.1 实验网络

本文通过在两种人工网络和两种实际网络上进行仿真实验,来评估IDB中心性度量措施的有效性.其中两个人工网络分别是BA无标度网络和WS小世界网络,两种实际网络分别为Stelzl网络和西部电网络,网络的部分参数见表1.

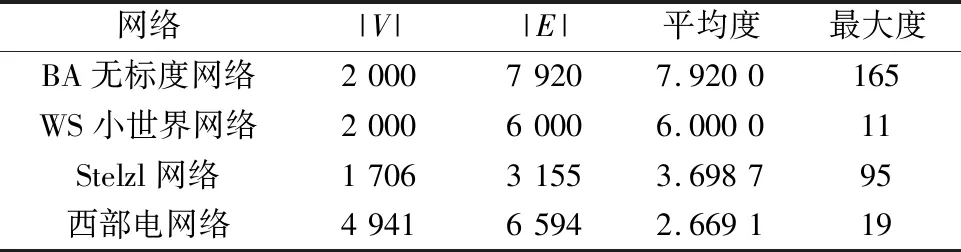
表1 四种网络的部分参数特性Tab.1 Partial parameter characteristics of four networks

2.2 评价标准

本文使用最大连通子图的相对大小作为节点重要性评价标准.连通子图指的是存在于网络的一个子图,在这个子图内,任意两个节点之间都至少存在一条简单路径.对于非连通的图,可以将其分解成两个或者两个以上的联通分支.其中各连通分支中包含节点最多的分支称为最大连通分支,也称为最大连通子图.

网络会随着中心节点的移除而分裂成若干个不连通的子图,其中最大连通子图的节点个数和网络的整体结构密切相关,最大连通子图的节点个数越少,就代表网络被损毁得越严重.最大连通子图相对大小被定义为

(5)

3 实验方法及结果分析

3.1 确定最优参数组合

在确定最优参数组合的过程中,首先得到729组参数组合下的IDB动态攻击效果.然后根据单一指标的攻击效果,选出在各个网络中攻击效果相对较好的单一指标.最后将每组参数组合下的IDB动态攻击效果与当前效果较好的单一指标的动态攻击效果作元素距离差Distance.例如,在BA无标度网络下,单一攻击策略攻击效果较好的指标是BC,则Distance定义为

Distance(i)=IDB(i)-BC(i)

(6)

其中：IDB和BC分别为BC指标和IDB指标对BA网络进行动态攻击时生成的最大连通子图相对大小的序列；i为IDB和BC序列的元素序号.所谓的攻击效果好就是在删除同样比例的节点,剩余网络的最大连通子图的相对大小越小越好,在对比图中反映的效果就是IDB生成的曲线有部分在BC生成的曲线下方,反映到元素距离差中的效果就是Distance(i)<0,Distance序列中小于零的元素个数越多,IDB的攻击效果就越好.实验中需要统计每个参数组合生成的Distance序列中小于零的元素个数Num(Distance(i)<0),并找出其最大值Nummax(Distance(i)<0)及其对应的参数组合.这样的参数组合可能有多组,将符合条件的参数组合所对应的IDB指标的动态攻击效果进行对比分析,最终确定最优放缩参数组合.

经过实验,在BA无标度网络下Nummax(Distance(i)<0)=38,其对应的参数(a，b，c)组合为154,155,164,174,175,184,185,186,187,195,199；在WS小世界网络下Nummax(Distance(i)<0)=27,其对应的参数(a,b,c)组合为162,172,181,182,192,232；在Stelzl网络下Nummax(Distance(i)<0)=11,其对应的参数(a，b，c)组合为129,225,236；在西部电网络下Nummax(Distance(i)<0)=26,其对应的参数(a，b，c)组合为119,218.从图1和表2可以看出,在BA网络中,参数组合为155的IDB指标攻击效果最佳.在WS网络中,参数组合为162、172、182、192的IDB指标攻击效果最佳,从运算时间和空间上考虑,相同攻击效果下,参数取值越小,攻击效率越佳,所以可以确定在WS网络下攻击效果最佳的放缩参数组合为162.在Stelzl网络中,参数组合为236的IDB指标攻击效果最佳.在西部电网络中,参数组合为218的IDB指标攻击效果最佳.

表2 动态攻击下各网络最先达到特定最大连通子图相对大小的参数组合Tab.2 The index that each network is the first to reach the relative size of the largest connected subgraph under dynamic attack

图1 Nummax(Distance(i)<0)对应的IDB指标动态攻击下网络最大连通子图的相对大小Fig.1 The relative size of the maximum connected subgraph under dynamic attack by Nummax (Distance(i)<0) corresponding IDB index

3.2 对比试验结果分析

在这组实验中,通过对比4种网络在BC、DC、KC、ISI、IDB五种指标的攻击效果,分析新的攻击策略对网络的破坏性.实验中,利用动态攻击的方式每次移除20个节点,通过对比移除过程中4种网络模型的最大连通子图的相对大小的变化情况来分析5种攻击策略的攻击效率.图2表示的是根据动态攻击从网络中去除节点时最大连通子图的相对大小的变化(即各指标动态攻击效果图).从表3中可知,在动态攻击的情况下,在BA无标度网络、WS小世界网络、Stelzl网络和西部电网络中,本文提出的IDB指标的攻击效果都是最佳的,能使网络快速崩溃,能够很好地识别网络节点的重要性.

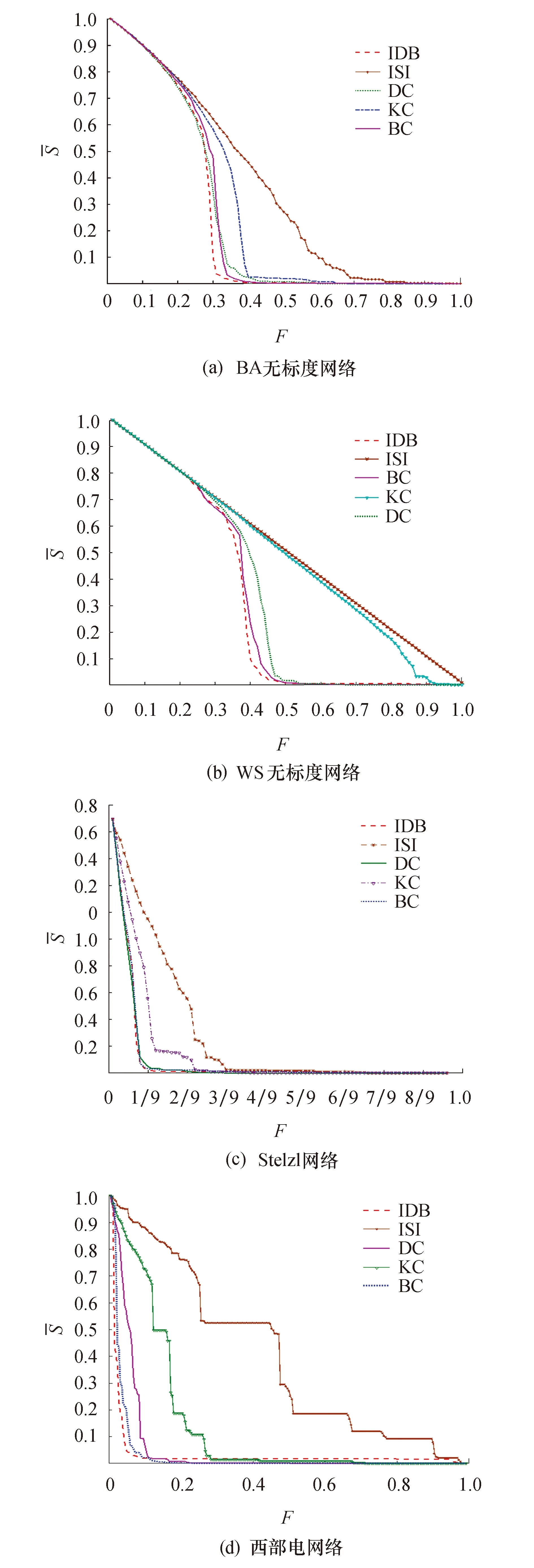
图2 五种指标的动态攻击效果图Fig.2 Effect of dynamic attack of five indexes

表3 动态攻击下各网络最先达到特定最大连通子图相对大小的指标Tab.3 The index that each network first reaches the relative size of the largest connected subgraph under dynamic attack

3.3 实验耗时分析

本实验的实验平台为联想G500个人笔记本电脑,处理器为Corei5-3230处理器,运行内存为8G；软件开发平台为MATLAB R2014a.表4为各实验过程所耗费的时间,时间统计以Matlab中程序实际运行时间为准.

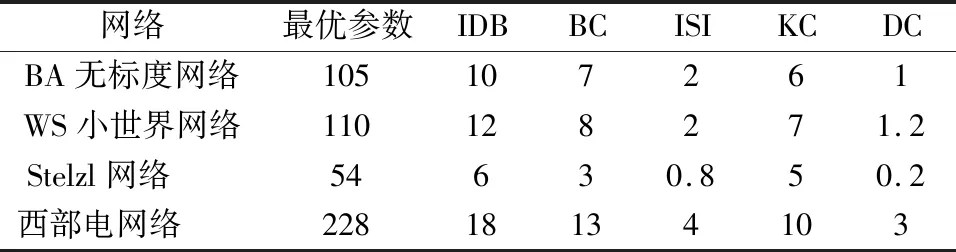
表4 各实验过程所耗费时间Tab.4 The time spent in each experimental process h

在确定各网络最优参数时程序并发执行,占用CPU和内存较大,因此对程序运行的耗时有一定的影响.在确定最优参数的过程中需要进行729组动态攻击实验,由于动态攻击中每删除20个节点都需要重新计算当前指标的值,所以在该试验过程中耗时较长.在五种指标动态攻击效果的对比试验中,组合中心性指标IDB比各单一指标攻击所耗时间均多.从IDB指标的定义来看其耗时有三部得分组成,即在动态攻击时要分别计算ISI、BC和DC指标,但是IDB指标动态攻击时实际消耗时间比单一指标ISI、BC和DC动态攻击所耗时间总和要少.总的来说,组合中心性指标IDB与单一中心性准则相比,它能够得到更准确、更全面的结果.

4 结论

本文基于ISI、DC、BC提出了一种新的组合中心性度量措施IDB.新的组合中心性度量措施IDB从节点自身、邻居和全局三方面考虑了网络中节点的重要性,并利用动态攻击方式对5种网络进行仿真实验.实验结果表明,与单一中心性准则相比,新定义的组合中心性指标IDB能够得到更准确、更全面的结果.