湍流度对水平轴风力机尾流及转矩特性的影响

李德顺, 苏进诚, 李银然, 郭 涛

(1. 兰州理工大学 能源与动力工程学院, 甘肃 兰州 730050; 2. 兰州理工大学 甘肃省风力机工程技术研究中心, 甘肃 兰州 730050; 3. 兰州理工大学 甘肃省流体机械及系统重点实验室, 甘肃 兰州 730050)

尾流效应是影响风电场发电效率的重要因素,而来流湍流度是影响水平轴风力机尾流特性的重要参数之一.湍流度是风速的标准偏差与平均风速的比率.受大气环境、地表粗糙度等影响,不同风场来流湍流度大小及分布不尽相同.因此,研究湍流度对水平轴风力机尾流特性的影响具有重要意义.

近年来,相关学者针对风力机尾流做了大量研究.Sorensen等[1]考虑叶片展向和旋转方位角的变化,提出了致动线模型.Keck[2]和Ameur等[3]耦合RANS模型和致动线模型对风力机尾流进行了相关研究.Ivanell等[4]采用大涡模拟结合致动线的方法对风力机的尾流叶尖涡进行了稳定性分析.MO等[5]研究了来流速度对风力机尾流稳定性的影响,发现尾涡破碎的位置与来流速度呈函数关系.HUN等[6]通过实验测量的方法,研究了湍流对水平轴风力机尾流及功率特性的影响,发现湍流来流时下游风力机的功率输出小于均匀来流时的功率输出,且与风力机纵向间距呈非线性关系.Talavera等[7]通过风洞实验分别研究了不同湍流来流对单台及两台串列风力机功率和尾流恢复的影响.王胜军[8]基于ANSYS FLUENT平台开发了风力机风轮的致动线代码,研究了风力机不同排列情况下的尾流相互干涉特性.刚蕾等[9]基于Park模型尾流区线性膨胀假设和涡黏模型对尾流区径向风速呈高斯分布假设,提出一种Park-Gauss新模型,对单台风力机尾流进行了数值模拟.钱耀如等[10]利用致动线结合大涡模拟(LES)的方法研究了低湍流度均匀来流中两台串列风力机的气动性能、尾流干扰、功率系数和推力系数等,并验证了致动线结合大涡模拟研究风力机尾流的可靠性.章书成等[11]利用高频PIV系统测量风力机尾流数据,发现叶尖涡的耗散速度比中心涡要快,且叶尖涡存在“交互跳跃”现象.侯亚丽等[12]采用大涡模拟方法研究了有、无风切入流对风力机尾流湍流特征的影响.张旭耀等[13]通过数值模拟研究了一台水平轴风力机尾流的自相似性及流场特性.

本文为进一步研究来流湍流度对风力机尾流及转矩特性的影响,采用大涡模拟耦合致动线的方法模拟均匀来流及不同湍流度来流条件下的风力机尾流流场,并从尾流速度分布、尾流膨胀及风轮转矩三个方面研究湍流度对风力机尾流及转矩特性的影响规律.

1 数值模型

1.1 致动线模型

致动线模型由致动盘模型改进而来,将旋转的叶片简化为旋转的致动线,在叶片上布置若干计算点,并利用BEM理论计算各计算点处的气动力,计算点处的气动力可以表示为

(1)

式中：W为叶片上某翼型的相对入流速度;c为计算点处翼型弦长;空气密度为1.225 kg/m3;CL、CD分别为翼型的升力系数和阻力系数;eL、eD分别为升力和阻力方向的单位向量.

为防止数值振荡,需将体积力光滑分布到周围的网格上,因此采用Gaussian光顺函数将叶素上的作用力光顺过渡到周围网格上.Gaussian光顺函数为

(2)

则计算点作用于流体的体积力可以表示为

fi=fe⊗ηε(d)

(3)

式中：fi将作为N-S方程中的源项;d为体积力;fi为作用点与叶片力气动力fe作用点之间的距离；ε是光顺函数长度尺度因子,表示高斯分布中调整叶片作用力集中程度的参数,ε越大,体积力分布越平滑,体积力影响范围越大.

1.2 大涡模拟

相较于雷诺平均(RANS)方法,LES方法更容易捕捉各物理量的脉动特征.Rethore[14]对比研究了RANS模型和LES模型,发现LES模型可以更好地捕捉多风力机尾流的掺混及速度恢复,计算得到的平均速度和湍流场更接近实验结果.因此本文基于LES方法研究风力机尾流及载荷特性.

LES方法通过某种滤波函数将大尺度的涡和小尺度的涡分离,滤波一般采用积分运算来实现.在自然风况下,流经风力机的风速低于音速,因此,风力机周围的气流可以看作不可压缩流体.则过滤后的连续方程可以表示为

(4)

不可压缩N-S方程为

(5)

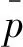
(6)

建立亚格子应力模型是大涡模拟的核心,本文采用Smagorinsky模型对亚格子应力进行模拟计算,该模型为

(7)

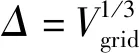
(8)

其中,滤波操作采用盒式滤波[15]表达式如下:

(9)

式中:x′i为小尺度空间坐标;xi为网格节点坐标;Δi为i方向上网格步长.

2 计算域及边界条件

2.1 研究对象

本文采用兰州理工大学景泰实验基地的一台33 kW水平轴风力机为研究对象,其主要参数见表1.

表1 风力机主要参数

2.2 计算域

本文采用长方体计算域,长224 m,宽、高均为36 m,风轮位于距计算域入口24 m处的截面中心,如图1所示.考虑到计算资源等各方面因素,将网格尺寸设为0.5 m,并将如图所示的阴影区域加密一次,最小网格尺寸为0.25 m.

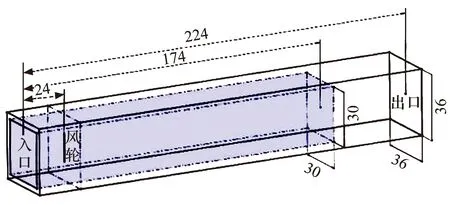
图1 计算域示意图Fig.1 Diagram of computational domain

2.3 边界条件

采用OpenFOAM中turbulentIletFvPatchField库设置入口速度,平均速度设为11 m/s,入口速度类型为turbulentIlet,采用Neumann压力条件；出口边界为Dirichlet压力条件和Neumann速度条件；时间步长0.01 s.通过在来流方向添加随机扰动产生脉动风速,对应的表达式为

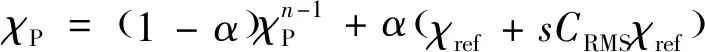
(10)

式中：χP和χref分别表示扰动速度添加网格位置和网格参考点;n表示时间步;α为扰动值,取值0.1;s表示扰动强度,与不同网格点处的脉动尺度有关;CRMS表示REM系数

(11)

本文通过改变x,y,z方向上的脉动尺度来模拟不同湍流度来流,脉动尺度为(0.02，0.01，0.01)、(0.2，0.1，0.1)和(0.5，0.2，0.2)时对应得到湍流度为0.85%、5.2%和10.3%.

3 结果与分析

3.1 风力机尾流场速度分布特性分析

为研究湍流度对风力机尾流速度分布特性的影响,本文对均匀来流及来流湍流度为0.85%、5.2%及10.3%时的风力机尾流轴向速度分布进行分析.图2为均匀来流及来流湍流度为0.85%、5.2%及10.3%时的风力机尾流轴向速度云图,图中X为风轮下风向某断面与风轮平面的轴向距离,D为风轮直径.由图可知,在均匀来流及湍流来流条件下,尾流区均产生了明显的速度亏损(尾流轴向时均速度与来流轴向时均速度的差值,时均速度表示120 s内轴向速度时均值).均匀来流时,尾流边界在整个流场内比较规则,这是因为均匀来流时尾流与周围流动掺混较慢；受风轮旋转影响,在风轮后0～2D范围内,尾流速度存在明显的波动,随后逐渐趋于平稳,这是因为风轮后产生了周期性的脱落涡,随后不断耗散,使得周期性波动逐渐消失.来流湍流度为0.85%时,在0～1.5D范围内存在明显波动,随后逐渐趋于平稳,从7D开始,尾流边界变得不规则,这是因为湍流尾流向后发展的过程中,尾涡逐渐耗散,尾流不断与周围流动发生掺混.来流湍流度为5.2%时,尾流边界在距风轮平面4D附近就已变得不规则.来流湍流度为10.3%时,尾流边界在距风轮平面2D附近就已变得不规则,尾流速度在距风轮平面13D处已基本恢复到来流风速.可以看出,随着来流湍流度增大,尾流与周围流动的能量交换加强,掺混速度加快,尾流恢复加快.

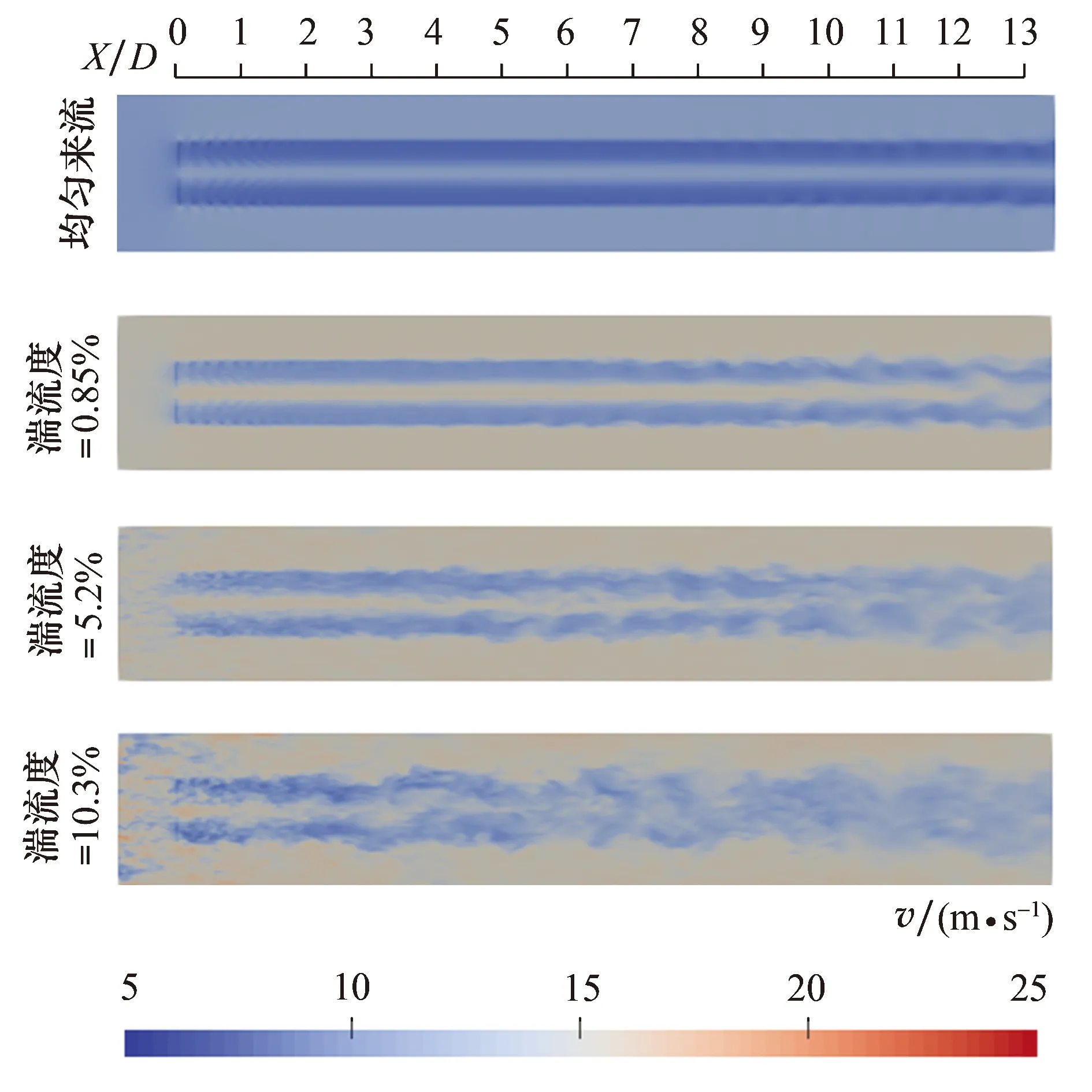
图2 轴向速度云图Fig.2 Axial velocity contours

图3为均匀来流与来流湍流度为0.85%、5.2%及10.3%时的风力机尾流速度廓线及尾流边界的对比图,图中Y为距风轮轴线的径向距离,R为风轮半径,v为尾流轴向时均速度,v0为来流速度,黑色、红色虚线分别代表均匀来流和湍流来流时的尾流边界.可以看出,在不同来流条件下,风轮后均出现明显的速度亏损,近尾流区速度廓线呈W型分布,随着流动向后发展,逐渐趋于V型分布[16].尾流速度最大亏损出现在风轮后1D附近.均匀来流时,尾流速度最大亏损率(尾流速度最大亏损值与来流速度的比值)为26%；来流湍流度为0.85%、5.2%及10.3%时,尾流速度最大亏损率分别为23.8%、24.1%及23.9%.这说明湍流会使尾流速度最大亏损率减小,但湍流度大小对尾流速度最大亏损率影响很小.均匀来流时,在风轮后7D处尾流速度恢复为来流风速的75%;来流湍流度分别为0.85%、5.2%及10.3%时,在风轮后7D处,尾流速度分别恢复至来流风速的78%、82%及83%.这说明来流湍流度会加速尾流速度的恢复,原因在于,湍流来流时,风力机尾流与周围流场的能量交换比均匀来流时更强,湍流掺混速度更快.定义尾流半径为尾流中心线到尾流边界(轴向速度为来流速度99%处)的距离,可以看到,尾流半径在风轮后0～1D范围内的增长速度逐渐减小,在1D之后尾流半径基本呈线性增长.在风轮后7D处,均匀来流时,尾流半径相对风轮半径增大19.5%；来流湍流度为0.85%、5.2%及10.3%时,尾流半径相对风轮半径增大26.8%、53.6%及78%.这说明随着来流湍流度增大,尾流区的膨胀程度增大,主要原因在于,随着来流湍流度的增大,尾流与周围流动的能量交换加强,掺混速度加快,导致尾流径向速度增大所引起.

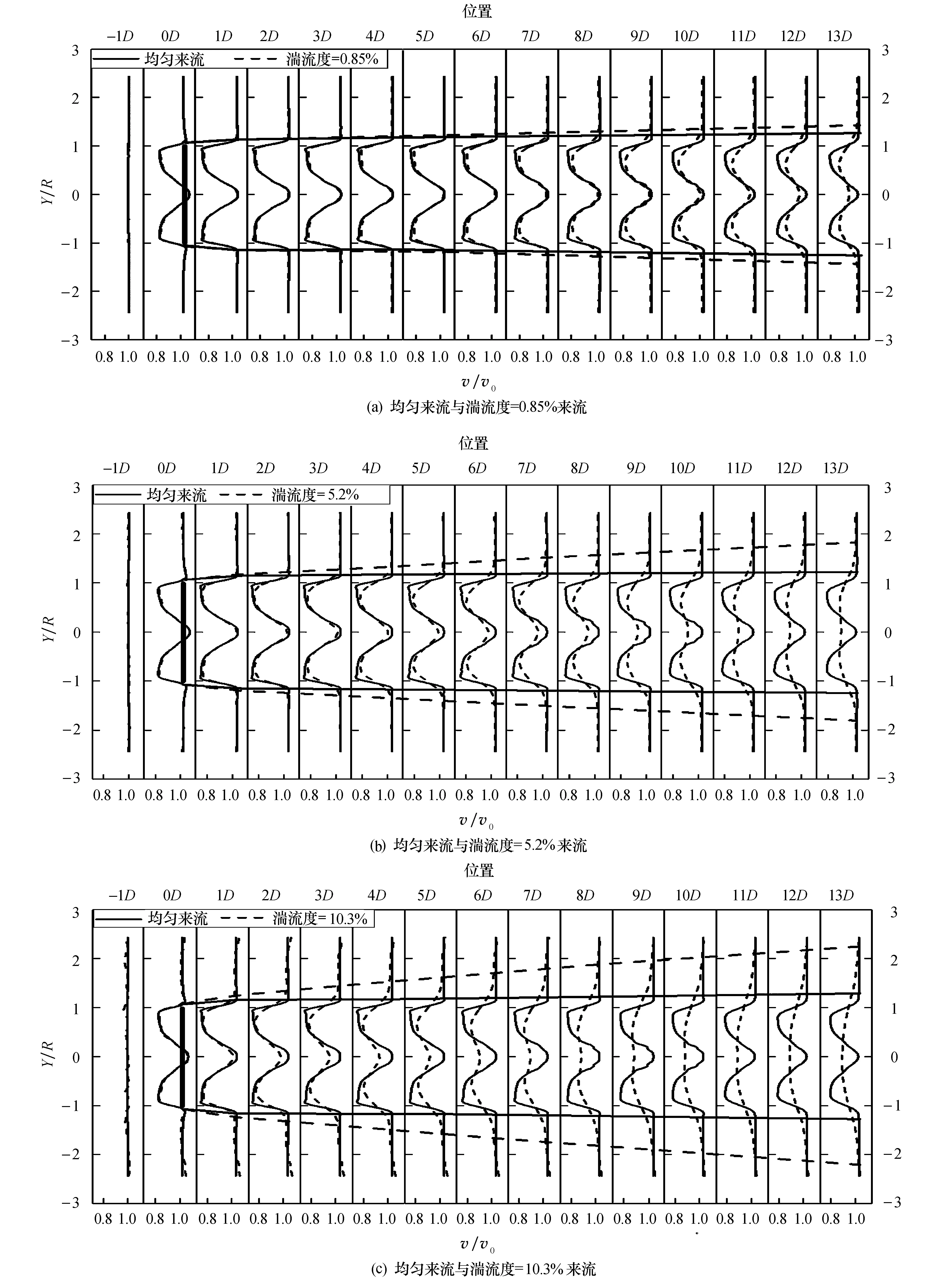
图3 均匀来流与不同湍流度来流尾流速度廓线及尾流边界对比Fig.3 Comparisons of velocity profile and wake boundary between uniform inflow and turbulent inflow

3.2 湍流度对风轮转矩特性的影响

来流湍流度对风轮转矩(风轮轴承受的转矩)影响较大,因此本节对不同来流湍流度条件下的风轮转矩特性开展研究.图4为均匀来流,0.85%、5.2%及10.3%湍流度来流时,风轮转矩的时程变化,红色水平线表示时均值.由图可知,均匀来流时,风轮转矩随时间呈现周期性波动,时均值为5 142 N·m,波动幅值为95 N·m,波动呈现明显的周期性变化.来流湍流度为0.85%、5.2%及10.3%时,风轮转矩时均值依次减小为4 807.6、4 762、4 701 N·m,这说明当风速为11 m/s时,随着湍流度增大,风轮转矩减小,风轮轴功率减小,该结论与文献[17]一致.来流时均风速不变,风轮转速不变,风轮轴功率降低,说明风轮的风能利用系数降低,即湍流度增大导致风轮的风能利用系数降低.来流湍流度为0.85%、5.2%及10.3%时,风轮转矩波动幅值依次为163、1 027、1 606 N·m,这说明随着湍流度增大,风轮转矩波动幅度增大,原因在于,随着来流湍流度的增大,风轮平面内流动各向异性增强,导致风力机叶片气动力波动加剧.

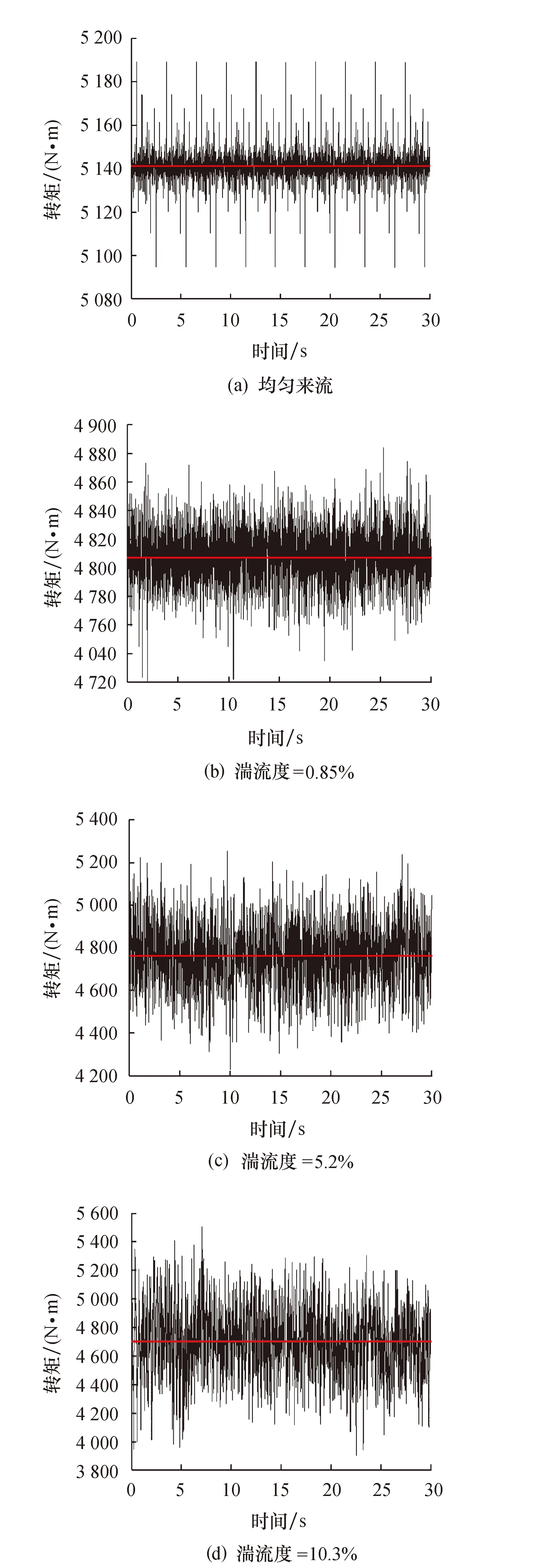
图4 风轮转矩时程图Fig.4 Time-history diagram of wind turbine torque

功率谱是信号的自相关函数的傅里叶变换,描述信号的能量特征随频率的变化关系,可以用来分析不同频率分量所携带的能量大小.图5为均匀来流与不同湍流度来流条件下风轮转矩的功率谱对比.可以看出,相较于均匀来流,湍流来流时风轮转矩的低频和高频能量增大,且湍流度越大能量越大,这是由于湍流脉动增大所导致.对比低频与高频能量分布,发现低频段能量增大得更快,原因在于湍流度增大时湍流尺度增大.均匀来流时风轮转矩功率谱呈现出很强的周期性,原因是均匀来流条件下风轮转矩的波动主要是由于尾流的诱导引起的.湍流来流时,功率谱出现了对应偶数倍转频的波峰:湍流度为0.85%时,两倍转频处出现波峰;湍流度为5.2%时,两倍、四倍转频处均出现波峰;湍流度为10.3%时,两倍、四倍转频处波峰对应的能量更高.可见,随着湍流度增大,偶数倍转频处出现波峰的现象更加明显,原因是湍流度增大时,风轮范围内风速分布的不对称性增强,由于风轮为两叶片,因此,风轮转矩呈现出偶数倍转频的波动增强.

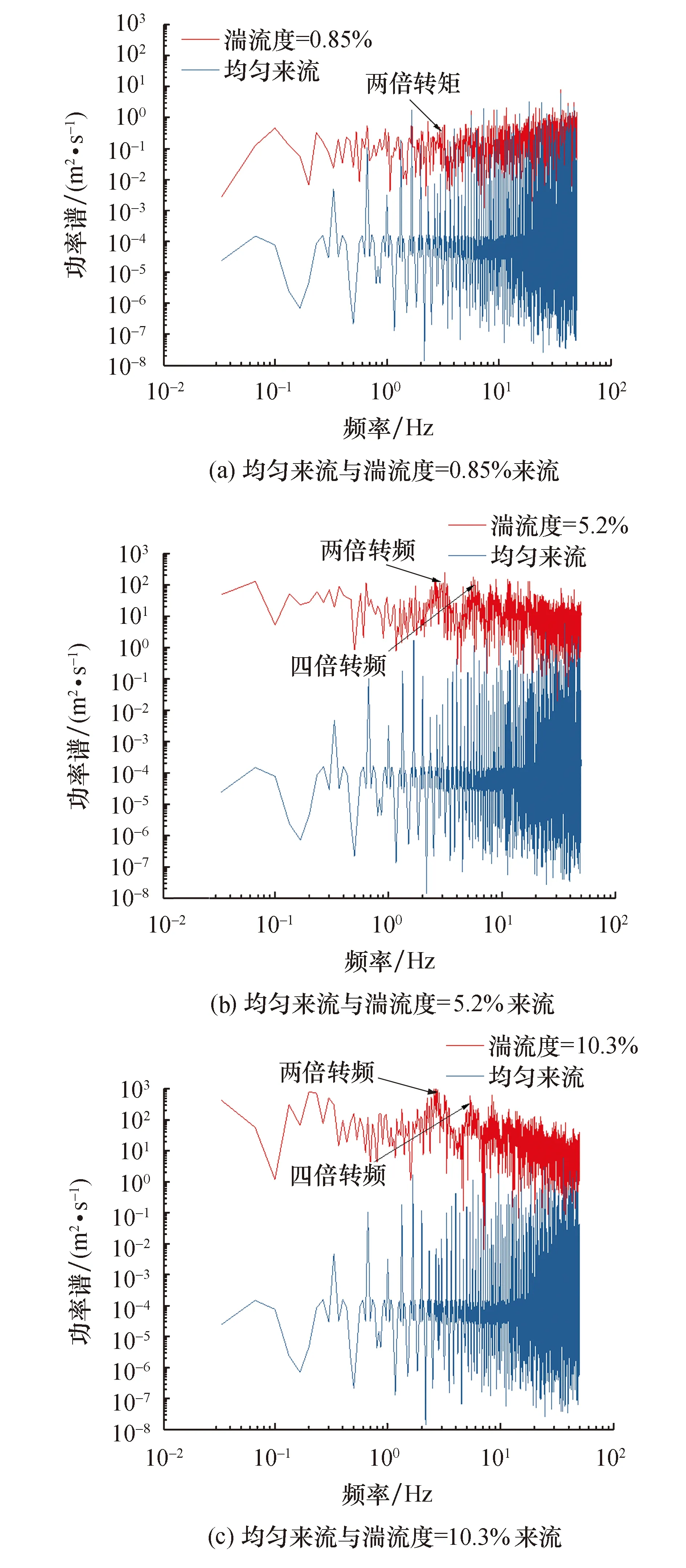
图5 风轮转矩功率谱对比图Fig.5 Comparison of torque power spectrum of wind turbine

4 结论

1) 均匀来流时,尾流恢复较慢；湍流来流时,风力机尾流与周围流场能量交换加强,湍流掺混速度变快,从而使得尾流恢复加快,且湍流度越大,恢复越快.同时,湍流会导致风力机尾流速度最大亏损率减小,但湍流度的大小对尾流速度最大亏损率影响很小.

2) 均匀来流时,尾流区膨胀程度较小,在风轮后7倍直径处,尾流半径相比风轮半径增大19.5%.来流湍流度为0.85%、5.2%及10.3%时,尾流半径相比风轮半径分别增大26.8%、53.6%及78%,表明湍流会使尾流膨胀程度增大,且湍流度越大,膨胀程度越大.

3) 风速为11 m/s时,随湍流度增大,风轮转矩时均值减小,波动增大；来流湍流度增大,风轮转矩的高频与低频部分能量增大,且低频部分能量增大地更快.