变参数趋近率的滑模模糊控制方法

李艳波，赵宇健，刘维宇，白 璘，惠 萌，黄伟峰

(1.长安大学电子与控制工程学院，陕西 西安 710064；2.中航电测一零一航空电子设备有限公司，陕西 汉中 723000)

0 引言

永磁同步电机(permanent magnet synchronous motor, PMSM)因其具有体积小、重量轻、功率高以及电机的形状和尺寸可以灵活多样等显著优点而得到广泛应用[1]。近年来，随着材料技术和电子电力技术的不断完善，永磁材料性能的不断提高，以及永磁同步电机现代控制理论的不断成熟，PMSM已经在民用、航天和军事领域得到了广泛应用[2]。然而，PMSM是一个容易受外界因素和自身系统参数影响的复杂对象[3]，为了获得较好的控制性能和动态品质，需要对其采用较优的控制方法来减小稳态误差，降低系统超调，使其按预定轨迹运动[4]。

滑模控制(sliding mode control)是变结构控制系统的一种控制方法[5]，这种控制方法与常规控制方法的根本区别在于控制的不连续性，即一种使系统结构随时间变化的开关特性[6]。滑模变结构控制系统由趋近模态和滑动模态两部分组成，在趋近运动阶段，系统误差不能得到有效的控制[7]，系统的超调与鲁棒性都会受到系统内部参数的影响，有效的趋近率会缩短系统趋近运动阶段的时间，因此设计一个较为有效的趋近率是解决电机不稳定因素的关键[8]。以往文献中所使用的常规传统指数趋近率[9-10]，系统的结构控制单一，但外部出现扰动时，PMSM的转矩和转速会出现一定的超调和抖动，抗干扰能力差。本文针对此问题，提出了变参数趋近率滑模模糊控制方法。

1 永磁同步电机的数学模型

三相PMSM的数学模型是一个比较复杂且强耦合的多变量系统，为了便于后期速度环的设计[11]，必须选择合适的坐标变换对系统进行降阶和解耦运算。为了模型的控制简便，我们通常采用忽略铁损的d、q轴基本数学模型[12]，以表贴式PMSM电机为例，如下式所示：

(1)

式(1)中，ud和uq分别为d、q轴上的电压；id和iq分别为d、q轴上的电流；对于表贴式PMSM来说，d、q轴上的电感相等，上式中都用Ls来表示；ψf为永磁体与定子交链磁链；R为定子绕组电阻；pn为电磁极对数[13]。

对于表贴式PMSM而言，通常采用id=0的转子磁场定向控制方法即可获得较好的控制效果，这时式(1)可变为如下数学模型：

(2)

2 控制方法

本文提出的改进控制方法的系统框图如图1所示。

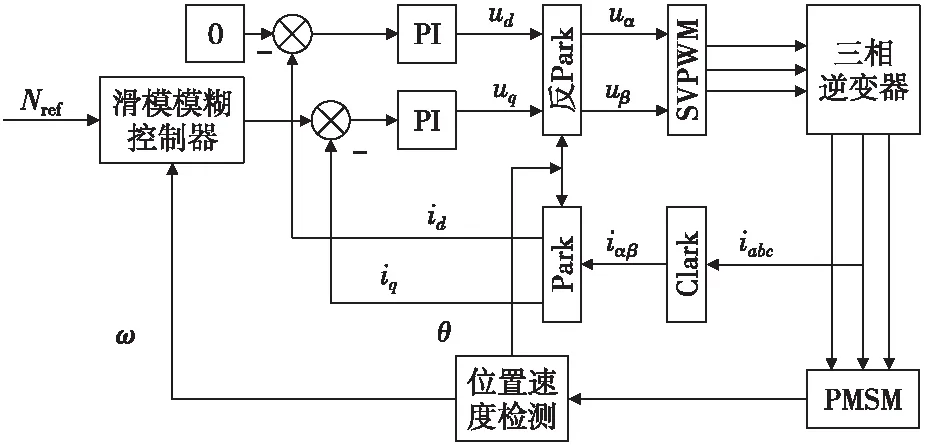
图1 控制策略系统框图Fig. 1 Block diagram of control policy system

根据上述内容，定义表贴式PMSM的系统状态变量来构造滑模函数[14]，通常将转速误差与其导数作为变量：

(3)

式(3)中，ωref为电机的参考转速，通常为固定值，ωm为实际转速。对式(3)进行求导可得：

(4)

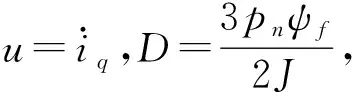
s=cx1+x2

(5)

式(5)中，c>0为系统待设计的参数。将传统的滑模趋近率将其改进为式(6)：

(6)

式(6)中，|x1|是系统状态变量；s为滑模面；k为趋近率系数(k>0)；α=Aε,β=Bε,其中A>0,B>0，通过模糊控制参数ε来控制系统趋近滑模面的速率；δ>0,0<ε<1。

设：

(7)

由式(7)可以看出当系统远离滑模面时，f(x1)≈k/ε>k，其趋近速率大于指数趋近率；当系统运动到接近滑模面时，系统状态变量|x1|趋近于零，滑模面s也趋近于零，即f(x1)也趋近于零，从而降低了系统的趋近速率，使其处于滑动模态，一定程度上减少系统的抖振[15]。

为了验证本文提出的新型趋近率的稳定性，定义李雅普诺夫方程为：

(8)

对式(8)进行求导可得：

(9)

根据李雅普诺夫稳定判据可得，系统在一定的时间内能够趋于稳定。

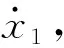
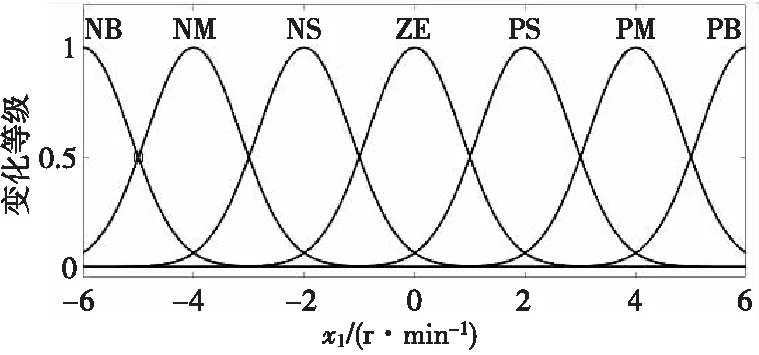
图2 输入变量x1及隶属度函数Fig. 2 Input variables and membership functions

图3 输入变量x2及隶属度函数Fig. 3 Input variables and membership functions

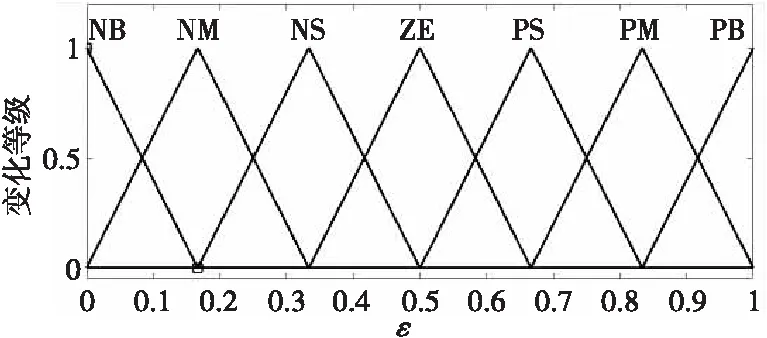
图4 输出变量ε及其隶属度函数Fig. 4 Output variables and their membership functions

模糊控制规则如表1所示。

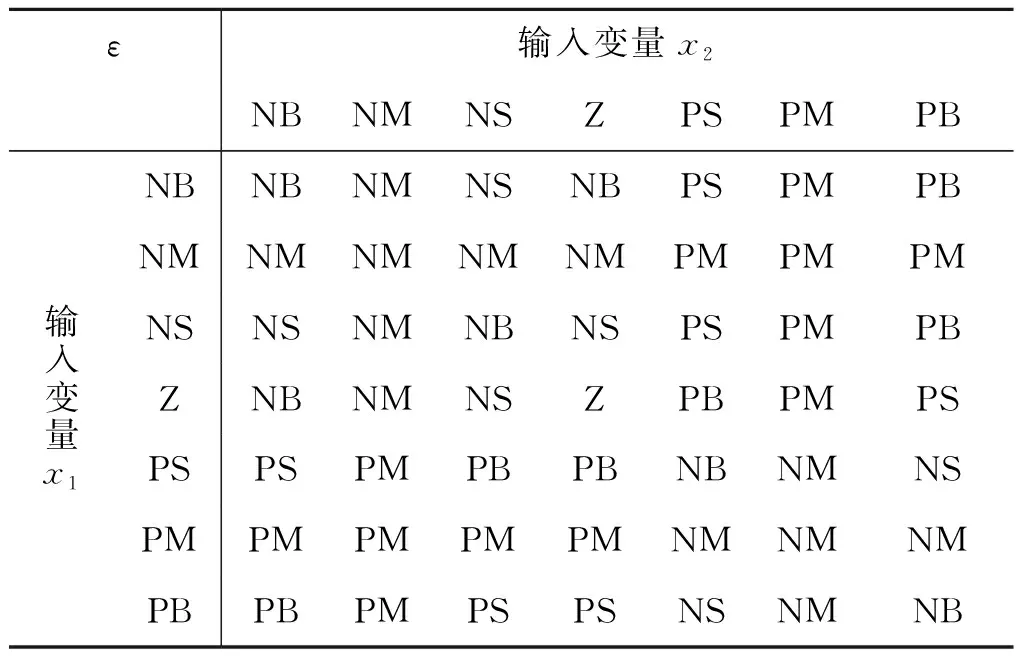
表1 模糊控制规则

表1中，NB表示输入变量x1、x2以及输出变量ε为负大，即表示变量值为负且偏大。同理，NM表示负中，NS表示负小；相对应的，PS表示正小，PM表示正中，PS表示正大，Z表示为零。

根据上述模糊控制规则可以通过两个系统输入变量来控制模糊参数ε，将系统的滑模趋近运动划为49个模块，较为全面地分析了可能出现的各类情况，更为系统地、精确地调节了滑模趋近率。同时可以控制参数α、β的值增强系统的抗干扰能力，减小系统的滑模抖振，使其按照预定的轨迹运动[18]。

根据式(4)、式(5)、式(6)可得，q轴的参考电流可表示为式(10)：

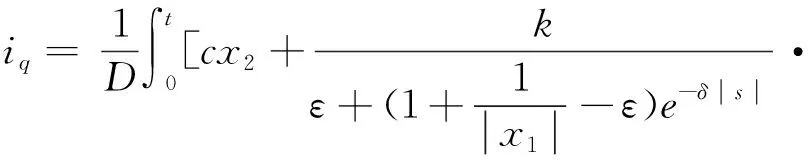
(10)

式(10)中包含的积分项可以削弱系统的稳态误差，增强系统的动态品质[19]。

3 实验仿真与结果分析

通过Matlab/Sinmulink对PMSM调速系统进行仿真建模，并以TMS320F2812为控制芯片搭建了实物系统[20]。通过仿真与实验结果来对比在指数趋近率下的转速、转矩、电机电流变化情况，验证本文提出的变参数趋近率的滑模模糊控制方法的有效性。PMSM的参数如表2所示。

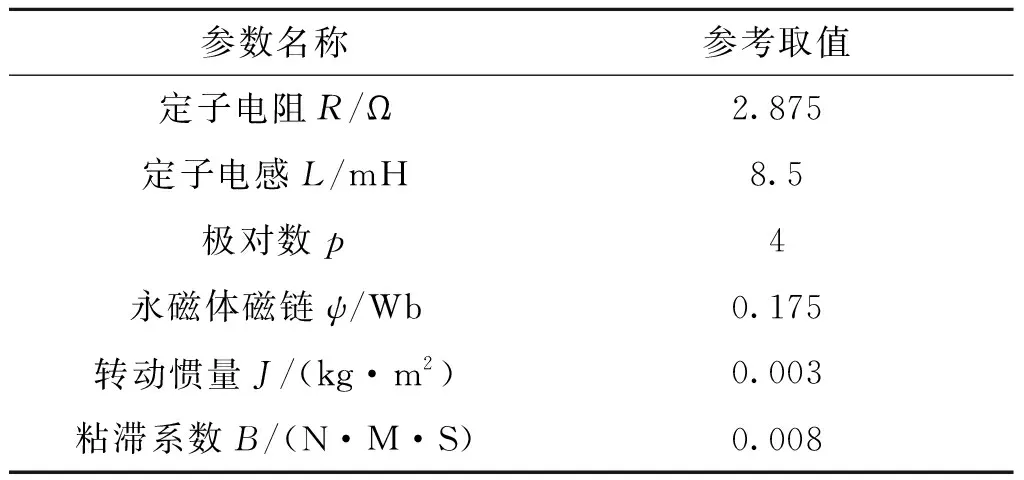
表2 PMSM的参数

在Sinmulink的仿真图当中，仿真条件设置为：直流侧电压U=311 V，PWM开关频率设置，采用周期设置为Ts=10 μs，采用变步长ode23tb算法，相对误差设置为0.000 1，仿真时间设置为0.4 s。参考转速Nref=1 000 r/min，初始时刻负载转矩为TL=0 N·m，在t=0.2 s 时负载转矩TL=10 N·m。传统指数控制方法的波形与变参数趋近率的滑模模糊控制方法的波形仿真结果分别如图5、图6所示，实验结果如图7所示。

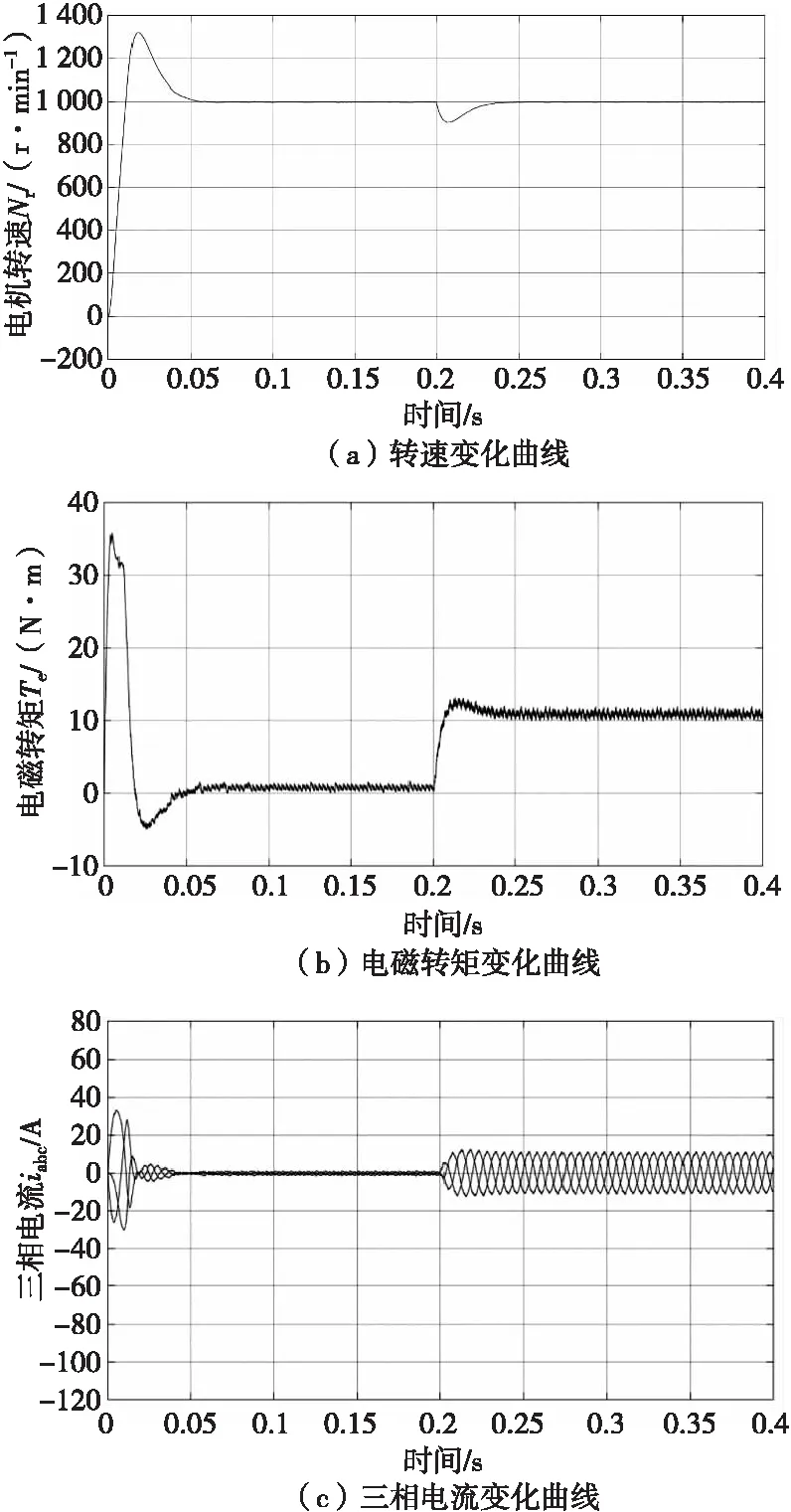
图5 SMC控制方法仿真结果Fig.5 Simulation results of SMC control system

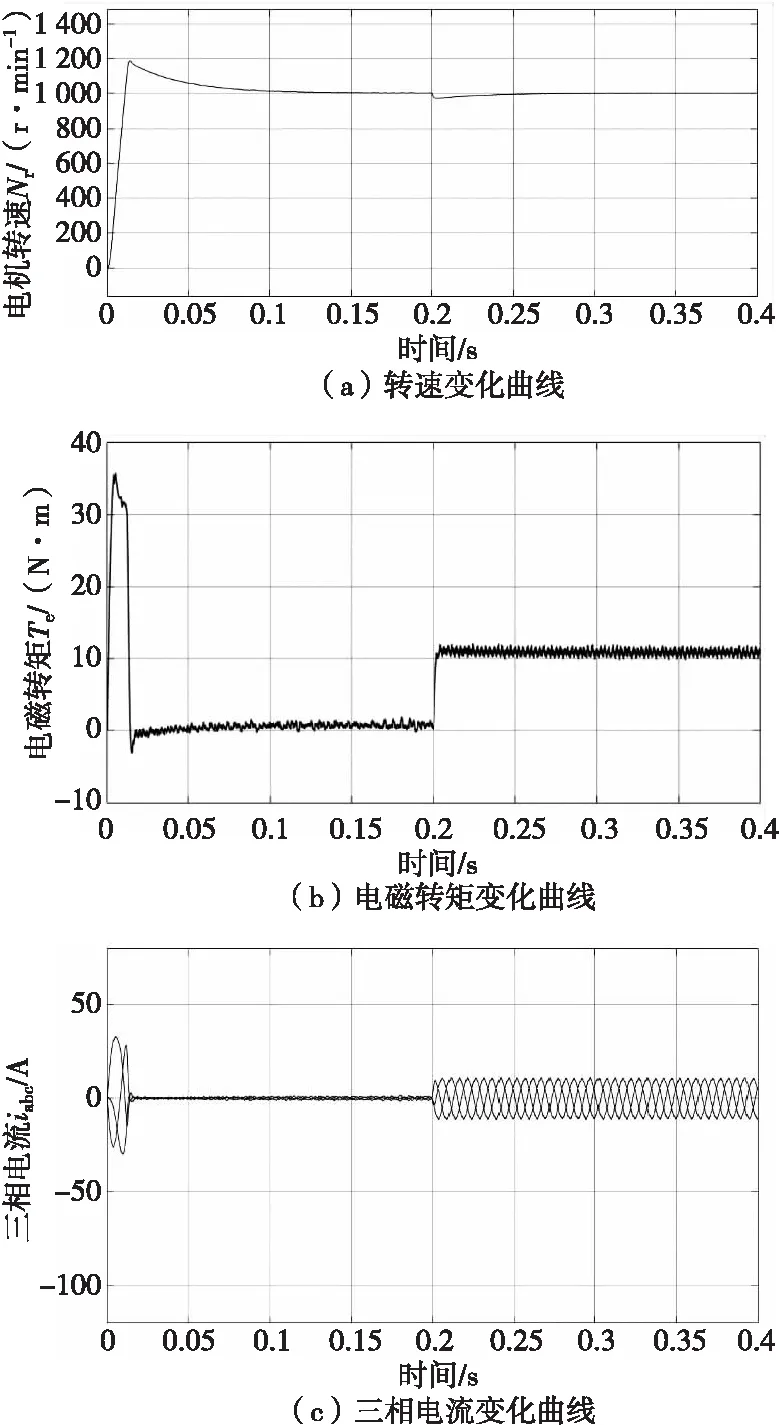
图6 变参数趋近率的滑模模糊控制方法仿真结果Fig. 6 Simulation results of variable parameter approach

图7 实验响应波形Fig.7 Experimental response waveform

系统的仿真时间设置为0～0.4 s，由仿真与实验结果波形可知，在SMC控制方法系统中，在电机启动阶段(t=0 s时刻)，电机的转速超调为1 355 r/min，当系统受到扰动时(t=0.2 s)，电机的电磁转矩超调为1.9 N/m，负载转速超调为 160 N/min。反观在变参数趋近率的滑模模糊控制方法下，当电机启动时，电机的转速超调为1 190 r/min，相比SMC控制系统下降12.18%；当电机受到外部干扰时，电机的转矩超调为1.3 N/m，相比SMC控制系统下降31.58%；负载转速超调为43 N/min，相比SMC控制方法下降73.12%。综上，在变参数趋近率的滑模模糊控制方法中，当系统启动和受到扰动时，电机的转矩和转速超调明显小于SMC控制方法，三相电流的抗干扰能力也优于SMC控制方法，受到扰动也能快速趋于稳定，较好地实现转速跟踪。

4 结论

本文提出了变参数趋近率的滑模模糊控制方法，该方法将模糊控制引入到滑模控制中，通过模糊规则来控制滑模系统里的参数来改进滑模趋近率，实现变参数滑模结构控制，减少系统到达滑模面的时间，有效地降低了滑模抖振。仿真实验结果表明，本文提出的变参数趋近率滑模模糊控制方法较常规SMC指数控制方法相比，系统转速、转矩和电流仿真波形均得到较大的改善，系统的自适应能力增强、超调减少，当受到外部干扰时也能快速地趋于稳定状态，恢复到给定参考转速值。从而说明所设计的变参数趋近率的滑模模糊控制方法具有较好的动态性能和抗干扰能力，满足电机控制性能的需求。